Contoh soal statistik non parametrik – Mempelajari statistik nonparametrik mungkin terasa rumit, tapi jangan khawatir! Artikel ini akan membawa Anda menjelajahi dunia statistik nonparametrik dengan contoh soal yang mudah dipahami. Kita akan membahas berbagai jenis uji, langkah-langkah penyelesaian, dan interpretasi hasil yang akan membantu Anda memahami konsep ini dengan lebih baik.
Bayangkan Anda ingin mengetahui apakah ada perbedaan signifikan antara dua metode pembelajaran yang berbeda pada sekelompok siswa. Statistik nonparametrik bisa menjadi alat yang tepat untuk menganalisis data tersebut, tanpa perlu asumsi yang ketat tentang distribusi data. Mari kita mulai dengan contoh soal yang menarik untuk menguji pemahaman Anda!
Pengertian Statistik Nonparametrik
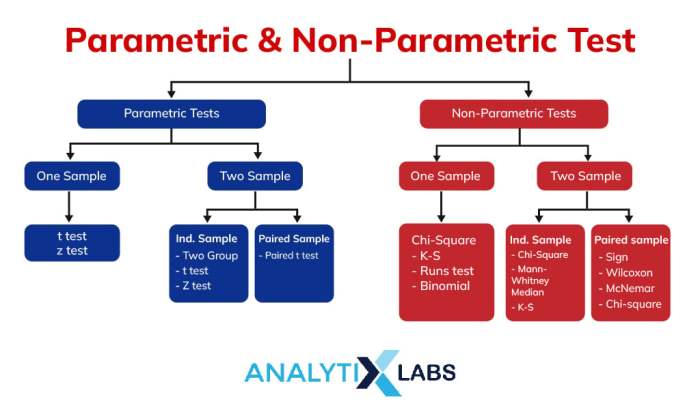
Statistik nonparametrik merupakan cabang ilmu statistik yang digunakan untuk menganalisis data yang tidak memenuhi asumsi distribusi normal. Dengan kata lain, statistik nonparametrik tidak bergantung pada bentuk distribusi data yang spesifik. Ini sangat berguna ketika kita tidak memiliki informasi yang cukup tentang distribusi data atau ketika data tidak memenuhi syarat untuk menggunakan metode statistik parametrik.
Perbedaan Statistik Parametrik dan Nonparametrik, Contoh soal statistik non parametrik
Untuk memahami lebih lanjut tentang statistik nonparametrik, kita perlu membandingkannya dengan statistik parametrik. Statistik parametrik mengasumsikan bahwa data berasal dari distribusi tertentu, seperti distribusi normal, dan menggunakan parameter untuk menggambarkan populasi. Contohnya, uji t dan ANOVA merupakan metode statistik parametrik.
| Karakteristik | Statistik Parametrik | Statistik Nonparametrik |
|---|---|---|
| Asumsi Distribusi Data | Mengasumsikan distribusi data tertentu (misalnya, distribusi normal) | Tidak mengasumsikan distribusi data tertentu |
| Parameter | Menggunakan parameter untuk menggambarkan populasi | Tidak menggunakan parameter |
| Jenis Data | Data interval atau rasio | Data nominal, ordinal, interval, atau rasio |
| Ukuran Sampel | Biasanya membutuhkan ukuran sampel yang besar | Dapat digunakan untuk ukuran sampel kecil |
| Uji Statistik | Uji t, ANOVA, regresi linier | Uji Wilcoxon, Kruskal-Wallis, uji chi-square |
Contoh Kasus Statistik Nonparametrik
Bayangkan Anda ingin membandingkan tingkat kepuasan pelanggan terhadap dua produk berbeda. Anda mengumpulkan data tentang tingkat kepuasan pelanggan, tetapi Anda tidak yakin apakah data tersebut berdistribusi normal. Dalam kasus ini, statistik nonparametrik seperti uji Wilcoxon akan menjadi pilihan yang tepat untuk menganalisis data tersebut.
Jenis-Jenis Uji Statistik Nonparametrik
Uji statistik nonparametrik merupakan jenis uji statistik yang tidak bergantung pada asumsi distribusi data tertentu. Artinya, uji ini dapat diterapkan pada data yang tidak mengikuti distribusi normal atau data yang memiliki skala pengukuran ordinal atau nominal. Uji nonparametrik sangat berguna ketika data tidak memenuhi asumsi uji parametrik, seperti uji t atau ANOVA.
Jenis-Jenis Uji Statistik Nonparametrik
Beberapa jenis uji statistik nonparametrik yang umum digunakan adalah:
- Uji Wilcoxon Signed-Rank Test
- Uji Mann-Whitney U Test
- Uji Kruskal-Wallis Test
- Uji Friedman Test
- Uji Chi-Square Test
Uji Wilcoxon Signed-Rank Test
Uji Wilcoxon Signed-Rank Test digunakan untuk membandingkan dua kelompok data yang berpasangan (paired data). Uji ini cocok untuk data yang tidak mengikuti distribusi normal, seperti data ordinal atau data yang memiliki skala pengukuran interval tetapi tidak memenuhi asumsi normalitas.
Contoh kasus:
Misalnya, kita ingin membandingkan tingkat kepuasan pelanggan sebelum dan sesudah program pelatihan. Kita dapat menggunakan uji Wilcoxon Signed-Rank Test untuk melihat apakah ada perbedaan signifikan antara tingkat kepuasan sebelum dan sesudah pelatihan.
Uji Mann-Whitney U Test
Uji Mann-Whitney U Test digunakan untuk membandingkan dua kelompok data yang independen (independent data). Uji ini cocok untuk data yang tidak mengikuti distribusi normal, seperti data ordinal atau data yang memiliki skala pengukuran interval tetapi tidak memenuhi asumsi normalitas.
Contoh kasus:
Misalnya, kita ingin membandingkan kinerja dua kelompok mahasiswa yang menggunakan metode pembelajaran yang berbeda. Kita dapat menggunakan uji Mann-Whitney U Test untuk melihat apakah ada perbedaan signifikan antara kinerja kedua kelompok mahasiswa.
Uji Kruskal-Wallis Test
Uji Kruskal-Wallis Test digunakan untuk membandingkan tiga atau lebih kelompok data yang independen (independent data). Uji ini cocok untuk data yang tidak mengikuti distribusi normal, seperti data ordinal atau data yang memiliki skala pengukuran interval tetapi tidak memenuhi asumsi normalitas.
Contoh kasus:
Misalnya, kita ingin membandingkan tingkat kepuasan pelanggan terhadap tiga jenis produk yang berbeda. Kita dapat menggunakan uji Kruskal-Wallis Test untuk melihat apakah ada perbedaan signifikan antara tingkat kepuasan pelanggan terhadap ketiga jenis produk.
Uji Friedman Test
Uji Friedman Test digunakan untuk membandingkan tiga atau lebih kelompok data yang berpasangan (paired data). Uji ini cocok untuk data yang tidak mengikuti distribusi normal, seperti data ordinal atau data yang memiliki skala pengukuran interval tetapi tidak memenuhi asumsi normalitas.
Contoh kasus:
Misalnya, kita ingin membandingkan efektivitas tiga jenis obat terhadap gejala penyakit tertentu. Kita dapat menggunakan uji Friedman Test untuk melihat apakah ada perbedaan signifikan antara efektivitas ketiga jenis obat.
Uji Chi-Square Test
Uji Chi-Square Test digunakan untuk menganalisis hubungan antara dua variabel kategorikal (categorical data). Uji ini cocok untuk data yang memiliki skala pengukuran nominal.
Contoh kasus:
Misalnya, kita ingin melihat apakah ada hubungan antara jenis kelamin dan preferensi terhadap jenis makanan tertentu. Kita dapat menggunakan uji Chi-Square Test untuk melihat apakah ada hubungan signifikan antara kedua variabel tersebut.
| Jenis Uji | Jenis Data | Tujuan Uji |
|---|---|---|
| Uji Wilcoxon Signed-Rank Test | Data Berpasangan | Membandingkan dua kelompok data yang berpasangan |
| Uji Mann-Whitney U Test | Data Independen | Membandingkan dua kelompok data yang independen |
| Uji Kruskal-Wallis Test | Data Independen | Membandingkan tiga atau lebih kelompok data yang independen |
| Uji Friedman Test | Data Berpasangan | Membandingkan tiga atau lebih kelompok data yang berpasangan |
| Uji Chi-Square Test | Data Kategorikal | Menganalisis hubungan antara dua variabel kategorikal |
Asumsi Uji Statistik Nonparametrik
Uji statistik nonparametrik merupakan jenis uji statistik yang tidak bergantung pada asumsi distribusi data. Artinya, data tidak perlu mengikuti distribusi normal atau distribusi lainnya yang spesifik. Hal ini membuat uji statistik nonparametrik lebih fleksibel dan dapat diterapkan pada berbagai jenis data, termasuk data ordinal, nominal, atau data yang tidak terdistribusi normal.
Namun, meskipun tidak bergantung pada asumsi distribusi data, uji statistik nonparametrik tetap memiliki asumsi dasar yang harus dipenuhi untuk memastikan hasil uji yang valid dan akurat.
Asumsi Dasar Uji Statistik Nonparametrik
Berikut adalah asumsi dasar yang harus dipenuhi dalam melakukan uji statistik nonparametrik:
- Data harus independen. Artinya, pengukuran satu data tidak boleh memengaruhi pengukuran data lainnya.
- Data harus berasal dari populasi yang sama. Artinya, data harus memiliki karakteristik yang sama, meskipun mungkin memiliki nilai yang berbeda.
- Data harus terdistribusi secara acak. Artinya, data tidak boleh memiliki pola atau tren tertentu.
Perbandingan Asumsi Uji Statistik Parametrik dan Nonparametrik
Berikut adalah tabel yang merangkum asumsi yang diperlukan untuk setiap jenis uji statistik parametrik dan nonparametrik:
| Asumsi | Uji Statistik Parametrik | Uji Statistik Nonparametrik |
|---|---|---|
| Distribusi Data | Data harus terdistribusi normal | Data tidak harus terdistribusi normal |
| Varians | Varians antar kelompok harus sama | Varians antar kelompok tidak harus sama |
| Skala Pengukuran | Data harus berskala interval atau rasio | Data dapat berskala nominal, ordinal, interval, atau rasio |
| Ukuran Sampel | Ukuran sampel harus cukup besar | Ukuran sampel dapat kecil atau besar |
Jenis Uji Statistik Nonparametrik dan Asumsinya
Setiap jenis uji statistik nonparametrik memiliki asumsi spesifik yang harus dipenuhi. Berikut adalah beberapa jenis uji statistik nonparametrik dan asumsinya:
- Uji Wilcoxon Signed-Rank: Uji ini digunakan untuk membandingkan dua kelompok data yang berpasangan. Asumsinya adalah data harus independen dan terdistribusi secara simetris.
- Uji Mann-Whitney U: Uji ini digunakan untuk membandingkan dua kelompok data yang tidak berpasangan. Asumsinya adalah data harus independen dan terdistribusi secara simetris.
- Uji Kruskal-Wallis: Uji ini digunakan untuk membandingkan lebih dari dua kelompok data yang tidak berpasangan. Asumsinya adalah data harus independen dan terdistribusi secara simetris.
- Uji Friedman: Uji ini digunakan untuk membandingkan lebih dari dua kelompok data yang berpasangan. Asumsinya adalah data harus independen dan terdistribusi secara simetris.
- Uji Chi-Square: Uji ini digunakan untuk menguji hubungan antara dua variabel kategorikal. Asumsinya adalah data harus independen dan frekuensi yang diharapkan harus setidaknya 5.
Cara Melakukan Uji Statistik Nonparametrik
Uji statistik nonparametrik merupakan metode analisis data yang tidak memerlukan asumsi tentang distribusi data. Metode ini cocok digunakan ketika data tidak berdistribusi normal atau ketika data berupa ordinal atau kategorikal. Uji statistik nonparametrik sering digunakan dalam berbagai bidang seperti ilmu sosial, kesehatan, dan bisnis.
Langkah-Langkah Umum dalam Melakukan Uji Statistik Nonparametrik
Secara umum, langkah-langkah dalam melakukan uji statistik nonparametrik adalah sebagai berikut:
- Merumuskan Hipotesis: Seperti halnya uji statistik parametrik, uji statistik nonparametrik juga membutuhkan hipotesis nol dan hipotesis alternatif. Hipotesis nol biasanya menyatakan bahwa tidak ada perbedaan atau hubungan antara variabel, sedangkan hipotesis alternatif menyatakan bahwa ada perbedaan atau hubungan.
- Memilih Uji yang Tepat: Ada banyak jenis uji statistik nonparametrik, dan pemilihan uji yang tepat bergantung pada jenis data, desain penelitian, dan tujuan analisis. Beberapa uji statistik nonparametrik yang umum digunakan meliputi Uji Wilcoxon, Uji Mann-Whitney, Uji Kruskal-Wallis, dan Uji Friedman.
- Menghitung Statistik Uji: Setiap uji statistik nonparametrik memiliki rumus atau prosedur yang spesifik untuk menghitung statistik uji. Statistik uji ini digunakan untuk menilai signifikansi hasil.
- Menentukan Nilai P: Nilai p adalah probabilitas mendapatkan hasil yang diamati atau lebih ekstrem jika hipotesis nol benar. Nilai p digunakan untuk menentukan apakah hipotesis nol ditolak atau tidak.
- Menarik Kesimpulan: Jika nilai p kurang dari tingkat signifikansi (biasanya 0,05), maka hipotesis nol ditolak, yang berarti bahwa ada bukti yang cukup untuk mendukung hipotesis alternatif. Sebaliknya, jika nilai p lebih besar dari tingkat signifikansi, maka hipotesis nol tidak ditolak.
Contoh Kasus: Membandingkan Efektivitas Dua Jenis Obat
Misalkan kita ingin membandingkan efektivitas dua jenis obat untuk mengobati sakit kepala. Kita memiliki dua kelompok pasien, masing-masing diberi salah satu jenis obat. Kita ingin mengetahui apakah ada perbedaan signifikan dalam efektivitas kedua obat tersebut.
Karena kita tidak dapat berasumsi bahwa data berdistribusi normal, kita dapat menggunakan Uji Mann-Whitney untuk membandingkan efektivitas kedua obat. Uji ini membandingkan peringkat median dari dua kelompok. Jika nilai p kurang dari 0,05, maka kita dapat menyimpulkan bahwa ada perbedaan signifikan dalam efektivitas kedua obat.
| Langkah | Penjelasan |
|---|---|
| 1. Merumuskan Hipotesis | H0: Tidak ada perbedaan signifikan dalam efektivitas kedua obat. H1: Ada perbedaan signifikan dalam efektivitas kedua obat. |
| 2. Memilih Uji yang Tepat | Uji Mann-Whitney |
| 3. Menghitung Statistik Uji | Menggunakan rumus Uji Mann-Whitney untuk menghitung statistik uji. |
| 4. Menentukan Nilai P | Menentukan nilai p berdasarkan statistik uji. |
| 5. Menarik Kesimpulan | Jika nilai p kurang dari 0,05, maka H0 ditolak. |
Interpretasi Hasil Uji
Setelah melakukan uji statistik nonparametrik, langkah selanjutnya adalah menginterpretasikan hasil yang diperoleh. Interpretasi ini penting untuk menentukan apakah hipotesis nol ditolak atau tidak, dan apa kesimpulan yang dapat diambil dari data yang dianalisis.
Cara Menginterpretasikan Hasil Uji
Interpretasi hasil uji statistik nonparametrik umumnya dilakukan dengan melihat nilai p (p-value). Nilai p menunjukkan probabilitas mendapatkan hasil uji yang sama atau lebih ekstrem daripada yang diamati, dengan asumsi bahwa hipotesis nol benar.
- Jika nilai p lebih kecil dari tingkat signifikansi (α), biasanya 0.05, maka hipotesis nol ditolak. Ini berarti bahwa ada bukti yang cukup untuk menolak hipotesis nol dan menerima hipotesis alternatif.
- Jika nilai p lebih besar dari tingkat signifikansi (α), maka hipotesis nol tidak ditolak. Ini berarti bahwa tidak ada bukti yang cukup untuk menolak hipotesis nol.
Selain nilai p, hasil uji juga dapat diinterpretasikan dengan melihat statistik uji dan derajat kebebasan. Statistik uji menunjukkan seberapa jauh data yang diamati menyimpang dari hipotesis nol, sedangkan derajat kebebasan menunjukkan jumlah informasi independen yang tersedia dalam data.
Contoh Interpretasi Hasil Uji
Berikut beberapa contoh interpretasi hasil uji untuk berbagai jenis uji statistik nonparametrik:
Uji Wilcoxon
Misalnya, pada uji Wilcoxon untuk data berpasangan, hipotesis nol menyatakan bahwa tidak ada perbedaan antara dua kelompok data. Jika nilai p lebih kecil dari 0.05, maka hipotesis nol ditolak, dan dapat disimpulkan bahwa terdapat perbedaan signifikan antara kedua kelompok data. Statistik uji menunjukkan seberapa besar perbedaan tersebut, dan derajat kebebasan menunjukkan jumlah pasangan data yang dianalisis.
Uji Mann-Whitney
Dalam uji Mann-Whitney untuk data independen, hipotesis nol menyatakan bahwa tidak ada perbedaan antara dua kelompok data. Jika nilai p lebih kecil dari 0.05, maka hipotesis nol ditolak, dan dapat disimpulkan bahwa terdapat perbedaan signifikan antara kedua kelompok data. Statistik uji menunjukkan seberapa besar perbedaan tersebut, dan derajat kebebasan menunjukkan jumlah data dalam masing-masing kelompok.
Uji Kruskal-Wallis
Pada uji Kruskal-Wallis untuk data independen dengan lebih dari dua kelompok, hipotesis nol menyatakan bahwa tidak ada perbedaan antara kelompok-kelompok data. Jika nilai p lebih kecil dari 0.05, maka hipotesis nol ditolak, dan dapat disimpulkan bahwa terdapat perbedaan signifikan antara setidaknya dua kelompok data. Statistik uji menunjukkan seberapa besar perbedaan tersebut, dan derajat kebebasan menunjukkan jumlah kelompok data yang dianalisis.
Hubungan Hasil Uji dan Kesimpulan
| Hasil Uji | Kesimpulan |
|---|---|
| Nilai p < α | Tolak hipotesis nol |
| Nilai p ≥ α | Tidak tolak hipotesis nol |
Penting untuk diingat bahwa interpretasi hasil uji harus selalu dilakukan dalam konteks penelitian. Selain nilai p, faktor-faktor lain seperti ukuran efek dan desain penelitian juga harus dipertimbangkan dalam menarik kesimpulan yang valid.
Contoh Soal Statistik Nonparametrik
Statistik nonparametrik merupakan cabang statistik yang digunakan untuk menganalisis data tanpa harus berasumsi tentang distribusi data. Metode ini sangat berguna ketika data tidak memenuhi asumsi distribusi normal, seperti data ordinal, nominal, atau data yang memiliki outlier ekstrem. Dalam artikel ini, kita akan membahas beberapa contoh soal statistik nonparametrik dan langkah-langkah penyelesaiannya.
Uji Wilcoxon Signed-Rank
Uji Wilcoxon signed-rank merupakan uji nonparametrik yang digunakan untuk membandingkan dua kelompok data yang berpasangan. Uji ini berguna ketika data tidak memenuhi asumsi normalitas atau ketika data berpasangan.
- Contoh Soal: Sebuah peneliti ingin mengetahui apakah ada perbedaan signifikan dalam tingkat stres sebelum dan sesudah mengikuti program meditasi. Ia mengukur tingkat stres 10 orang peserta sebelum dan sesudah mengikuti program meditasi. Data tingkat stres ditunjukkan pada tabel berikut:
| Peserta | Tingkat Stres Sebelum | Tingkat Stres Sesudah |
|---|---|---|
| 1 | 8 | 6 |
| 2 | 7 | 5 |
| 3 | 9 | 7 |
| 4 | 6 | 4 |
| 5 | 5 | 3 |
| 6 | 10 | 8 |
| 7 | 4 | 2 |
| 8 | 7 | 6 |
| 9 | 6 | 5 |
| 10 | 8 | 7 |
- Langkah-langkah Penyelesaian:
- Hitung selisih antara tingkat stres sebelum dan sesudah program meditasi untuk setiap peserta.
- Urutkan selisih dari yang terkecil hingga yang terbesar, tanpa memperhatikan tanda.
- Berikan peringkat pada selisih yang diurutkan, dengan peringkat 1 untuk selisih terkecil, peringkat 2 untuk selisih berikutnya, dan seterusnya.
- Hitung jumlah peringkat untuk selisih positif dan selisih negatif.
- Tentukan statistik uji Wilcoxon signed-rank, yaitu jumlah peringkat yang lebih kecil.
- Bandingkan statistik uji dengan nilai kritis yang diperoleh dari tabel distribusi Wilcoxon signed-rank.
- Jika statistik uji lebih kecil dari nilai kritis, maka hipotesis nol ditolak. Artinya, ada perbedaan signifikan dalam tingkat stres sebelum dan sesudah mengikuti program meditasi.
Ilustrasi: Dalam contoh soal ini, statistik uji Wilcoxon signed-rank adalah 10. Nilai kritis untuk uji dua sisi dengan α = 0,05 dan n = 10 adalah 8. Karena statistik uji lebih besar dari nilai kritis, maka hipotesis nol tidak ditolak. Artinya, tidak ada perbedaan signifikan dalam tingkat stres sebelum dan sesudah mengikuti program meditasi.
Uji Mann-Whitney U
Uji Mann-Whitney U merupakan uji nonparametrik yang digunakan untuk membandingkan dua kelompok data independen. Uji ini berguna ketika data tidak memenuhi asumsi normalitas atau ketika data tidak berpasangan.
- Contoh Soal: Seorang guru ingin mengetahui apakah ada perbedaan signifikan dalam skor ujian matematika antara siswa yang mengikuti metode pembelajaran tradisional dan siswa yang mengikuti metode pembelajaran berbasis teknologi. Ia mengambil sampel 10 siswa dari masing-masing kelompok dan mencatat skor ujian matematika mereka. Data skor ujian ditunjukkan pada tabel berikut:
| Kelompok | Skor Ujian |
|---|---|
| Tradisional | 75 |
| Tradisional | 80 |
| Tradisional | 70 |
| Tradisional | 85 |
| Tradisional | 90 |
| Tradisional | 75 |
| Tradisional | 80 |
| Tradisional | 75 |
| Tradisional | 85 |
| Tradisional | 90 |
| Teknologi | 85 |
| Teknologi | 90 |
| Teknologi | 80 |
| Teknologi | 95 |
| Teknologi | 100 |
| Teknologi | 85 |
| Teknologi | 90 |
| Teknologi | 95 |
| Teknologi | 100 |
- Langkah-langkah Penyelesaian:
- Gabungkan data dari kedua kelompok dan urutkan dari yang terkecil hingga yang terbesar.
- Berikan peringkat pada data yang diurutkan, dengan peringkat 1 untuk data terkecil, peringkat 2 untuk data berikutnya, dan seterusnya.
- Hitung jumlah peringkat untuk masing-masing kelompok.
- Tentukan statistik uji Mann-Whitney U, yaitu jumlah peringkat yang lebih kecil.
- Bandingkan statistik uji dengan nilai kritis yang diperoleh dari tabel distribusi Mann-Whitney U.
- Jika statistik uji lebih kecil dari nilai kritis, maka hipotesis nol ditolak. Artinya, ada perbedaan signifikan dalam skor ujian matematika antara siswa yang mengikuti metode pembelajaran tradisional dan siswa yang mengikuti metode pembelajaran berbasis teknologi.
Ilustrasi: Dalam contoh soal ini, statistik uji Mann-Whitney U adalah 25. Nilai kritis untuk uji dua sisi dengan α = 0,05 dan n1 = n2 = 10 adalah 23. Karena statistik uji lebih besar dari nilai kritis, maka hipotesis nol tidak ditolak. Artinya, tidak ada perbedaan signifikan dalam skor ujian matematika antara siswa yang mengikuti metode pembelajaran tradisional dan siswa yang mengikuti metode pembelajaran berbasis teknologi.
Uji Kruskal-Wallis
Uji Kruskal-Wallis merupakan uji nonparametrik yang digunakan untuk membandingkan tiga atau lebih kelompok data independen. Uji ini berguna ketika data tidak memenuhi asumsi normalitas atau ketika data tidak berpasangan.
- Contoh Soal: Seorang peneliti ingin mengetahui apakah ada perbedaan signifikan dalam tingkat kepuasan pelanggan terhadap tiga merek produk yang berbeda. Ia mengambil sampel 10 pelanggan dari masing-masing merek dan mencatat tingkat kepuasan mereka. Data tingkat kepuasan ditunjukkan pada tabel berikut:
| Merek | Tingkat Kepuasan |
|---|---|
| A | 8 |
| A | 7 |
| A | 9 |
| A | 6 |
| A | 5 |
| A | 8 |
| A | 7 |
| A | 9 |
| A | 6 |
| A | 5 |
| B | 6 |
| B | 5 |
| B | 7 |
| B | 4 |
| B | 3 |
| B | 6 |
| B | 5 |
| B | 7 |
| B | 4 |
| B | 3 |
| C | 9 |
| C | 10 |
| C | 8 |
| C | 7 |
| C | 6 |
| C | 9 |
| C | 10 |
| C | 8 |
| C | 7 |
| C | 6 |
- Langkah-langkah Penyelesaian:
- Gabungkan data dari ketiga kelompok dan urutkan dari yang terkecil hingga yang terbesar.
- Berikan peringkat pada data yang diurutkan, dengan peringkat 1 untuk data terkecil, peringkat 2 untuk data berikutnya, dan seterusnya.
- Hitung jumlah peringkat untuk masing-masing kelompok.
- Tentukan statistik uji Kruskal-Wallis, yaitu H.
- Bandingkan statistik uji dengan nilai kritis yang diperoleh dari tabel distribusi Kruskal-Wallis.
- Jika statistik uji lebih besar dari nilai kritis, maka hipotesis nol ditolak. Artinya, ada perbedaan signifikan dalam tingkat kepuasan pelanggan terhadap tiga merek produk yang berbeda.
Ilustrasi: Dalam contoh soal ini, statistik uji Kruskal-Wallis adalah 12,5. Nilai kritis untuk uji tiga sisi dengan α = 0,05 dan k = 3 adalah 5,99. Karena statistik uji lebih besar dari nilai kritis, maka hipotesis nol ditolak. Artinya, ada perbedaan signifikan dalam tingkat kepuasan pelanggan terhadap tiga merek produk yang berbeda.
Uji Friedman
Uji Friedman merupakan uji nonparametrik yang digunakan untuk membandingkan tiga atau lebih kelompok data yang berpasangan. Uji ini berguna ketika data tidak memenuhi asumsi normalitas atau ketika data berpasangan.
Contoh soal statistik non parametrik seringkali menguji kemampuan kita dalam menganalisis data tanpa harus mengasumsikan distribusi data tertentu. Mirip dengan soal logika, yang menuntut kita berpikir kritis dan sistematis untuk menemukan solusi. Contoh soal logika dan jawabannya, seperti yang bisa kamu temukan di contoh soal logika dan jawabannya , bisa membantu kamu melatih kemampuan berpikir deduktif dan induktif yang juga dibutuhkan dalam menyelesaikan soal statistik non parametrik.
- Contoh Soal: Seorang peneliti ingin mengetahui apakah ada perbedaan signifikan dalam kinerja karyawan pada tiga metode pelatihan yang berbeda. Ia mengukur kinerja 10 karyawan pada masing-masing metode pelatihan. Data kinerja ditunjukkan pada tabel berikut:
| Karyawan | Metode A | Metode B | Metode C |
|---|---|---|---|
| 1 | 8 | 7 | 9 |
| 2 | 7 | 6 | 8 |
| 3 | 9 | 8 | 10 |
| 4 | 6 | 5 | 7 |
| 5 | 5 | 4 | 6 |
| 6 | 8 | 7 | 9 |
| 7 | 7 | 6 | 8 |
| 8 | 9 | 8 | 10 |
| 9 | 6 | 5 | 7 |
| 10 | 5 | 4 | 6 |
- Langkah-langkah Penyelesaian:
- Urutkan data untuk setiap karyawan dari yang terkecil hingga yang terbesar, tanpa memperhatikan metode pelatihan.
- Berikan peringkat pada data yang diurutkan, dengan peringkat 1 untuk data terkecil, peringkat 2 untuk data berikutnya, dan seterusnya.
- Hitung jumlah peringkat untuk masing-masing metode pelatihan.
- Tentukan statistik uji Friedman, yaitu χ2.
- Bandingkan statistik uji dengan nilai kritis yang diperoleh dari tabel distribusi Friedman.
- Jika statistik uji lebih besar dari nilai kritis, maka hipotesis nol ditolak. Artinya, ada perbedaan signifikan dalam kinerja karyawan pada tiga metode pelatihan yang berbeda.
Ilustrasi: Dalam contoh soal ini, statistik uji Friedman adalah 11,11. Nilai kritis untuk uji tiga sisi dengan α = 0,05 dan k = 3 adalah 5,99. Karena statistik uji lebih besar dari nilai kritis, maka hipotesis nol ditolak. Artinya, ada perbedaan signifikan dalam kinerja karyawan pada tiga metode pelatihan yang berbeda.
Uji Kolmogorov-Smirnov
Uji Kolmogorov-Smirnov merupakan uji nonparametrik yang digunakan untuk menguji apakah distribusi data sampel sesuai dengan distribusi tertentu. Uji ini berguna ketika data tidak memenuhi asumsi normalitas atau ketika data tidak berpasangan.
- Contoh Soal: Seorang peneliti ingin mengetahui apakah distribusi data tinggi badan siswa di suatu sekolah sesuai dengan distribusi normal. Ia mengambil sampel 50 siswa dan mencatat tinggi badan mereka. Data tinggi badan ditunjukkan pada tabel berikut:
| Tinggi Badan (cm) | Frekuensi |
|---|---|
| 150-155 | 5 |
| 155-160 | 10 |
| 160-165 | 15 |
| 165-170 | 10 |
| 170-175 | 5 |
| 175-180 | 5 |
- Langkah-langkah Penyelesaian:
- Hitung frekuensi kumulatif untuk setiap kelas interval.
- Hitung frekuensi kumulatif teoritis untuk setiap kelas interval, berdasarkan distribusi normal yang diasumsikan.
- Tentukan statistik uji Kolmogorov-Smirnov, yaitu D, yaitu selisih terbesar antara frekuensi kumulatif sampel dan frekuensi kumulatif teoritis.
- Bandingkan statistik uji dengan nilai kritis yang diperoleh dari tabel distribusi Kolmogorov-Smirnov.
- Jika statistik uji lebih besar dari nilai kritis, maka hipotesis nol ditolak. Artinya, distribusi data tinggi badan siswa tidak sesuai dengan distribusi normal.
Ilustrasi: Dalam contoh soal ini, statistik uji Kolmogorov-Smirnov adalah 0,15. Nilai kritis untuk uji dua sisi dengan α = 0,05 dan n = 50 adalah 0,13. Karena statistik uji lebih besar dari nilai kritis, maka hipotesis nol ditolak. Artinya, distribusi data tinggi badan siswa tidak sesuai dengan distribusi normal.
Perbedaan Uji Nonparametrik dan Parametrik
Dalam analisis statistik, kita seringkali dihadapkan pada pilihan antara menggunakan uji parametrik atau nonparametrik. Kedua jenis uji ini memiliki tujuan yang sama, yaitu untuk menguji hipotesis tentang populasi berdasarkan data sampel. Namun, keduanya menggunakan asumsi dan pendekatan yang berbeda, sehingga penting untuk memahami perbedaannya agar dapat memilih uji yang tepat untuk penelitian kita.
Perbedaan Asumsi Dasar
Perbedaan mendasar antara uji parametrik dan nonparametrik terletak pada asumsi yang mendasari kedua jenis uji ini. Uji parametrik umumnya memerlukan asumsi tentang distribusi data, seperti asumsi normalitas data atau kesamaan varians antar kelompok. Asumsi ini penting karena uji parametrik mengandalkan parameter populasi (misalnya, rata-rata dan deviasi standar) untuk membuat kesimpulan. Sebaliknya, uji nonparametrik tidak memerlukan asumsi yang ketat tentang distribusi data. Mereka bekerja dengan peringkat data atau frekuensi, sehingga lebih fleksibel untuk digunakan pada data yang tidak normal atau memiliki varians yang berbeda antar kelompok.
Situasi di mana Uji Nonparametrik Lebih Disarankan
Meskipun uji parametrik umumnya lebih kuat, uji nonparametrik memiliki keunggulan dalam situasi tertentu. Berikut beberapa situasi di mana uji nonparametrik lebih disarankan:
- Data tidak normal: Jika data tidak mengikuti distribusi normal, uji nonparametrik lebih tepat digunakan. Contohnya, jika data memiliki outlier atau distribusi yang miring, uji nonparametrik dapat memberikan hasil yang lebih akurat.
- Ukuran sampel kecil: Uji nonparametrik lebih cocok untuk ukuran sampel kecil, karena mereka tidak bergantung pada asumsi distribusi yang mungkin tidak terpenuhi pada sampel kecil.
- Data ordinal atau kategorikal: Uji nonparametrik dapat digunakan untuk menganalisis data ordinal atau kategorikal, yang tidak dapat diukur dengan skala interval atau rasio.
- Data yang tidak dapat diukur: Jika data tidak dapat diukur secara numerik, seperti data tentang preferensi atau pendapat, uji nonparametrik dapat digunakan untuk menganalisis data tersebut.
Tabel Perbedaan Utama
| Fitur | Uji Parametrik | Uji Nonparametrik |
|---|---|---|
| Asumsi Distribusi | Membutuhkan asumsi tentang distribusi data (misalnya, normalitas) | Tidak memerlukan asumsi tentang distribusi data |
| Jenis Data | Data interval atau rasio | Data ordinal, kategorikal, atau interval/rasio jika distribusi tidak normal |
| Ukuran Sampel | Cocok untuk ukuran sampel besar | Cocok untuk ukuran sampel kecil dan besar |
| Kekuatan Uji | Umumnya lebih kuat jika asumsi terpenuhi | Kurang kuat jika asumsi uji parametrik terpenuhi |
| Contoh Uji | Uji t, ANOVA, regresi linear | Uji Wilcoxon, Kruskal-Wallis, uji chi-square |
Kelebihan dan Kekurangan Uji Nonparametrik: Contoh Soal Statistik Non Parametrik
Uji statistik nonparametrik merupakan alat yang sangat berguna dalam analisis data, terutama ketika asumsi uji parametrik tidak terpenuhi. Penggunaan uji nonparametrik memberikan fleksibilitas dan ketahanan terhadap pelanggaran asumsi distribusi data. Namun, seperti metode statistik lainnya, uji nonparametrik juga memiliki kelebihan dan kekurangan yang perlu dipahami sebelum diterapkan.
Kelebihan Uji Nonparametrik
Uji nonparametrik memiliki beberapa kelebihan yang membuatnya menarik untuk diterapkan dalam analisis data:
- Tidak bergantung pada asumsi distribusi data: Uji nonparametrik tidak memerlukan asumsi distribusi data normal atau homogenitas varians, sehingga lebih fleksibel dan dapat digunakan untuk berbagai jenis data, termasuk data yang tidak normal atau memiliki varians yang tidak sama.
- Mudah diimplementasikan: Uji nonparametrik umumnya lebih mudah diimplementasikan dibandingkan dengan uji parametrik, terutama untuk data yang kompleks atau tidak terstruktur.
- Lebih tahan terhadap outlier: Uji nonparametrik lebih tahan terhadap outlier, data ekstrem yang dapat memengaruhi hasil uji parametrik.
- Cocok untuk data ordinal dan nominal: Uji nonparametrik dapat digunakan untuk menganalisis data ordinal dan nominal, sedangkan uji parametrik umumnya hanya cocok untuk data interval atau rasio.
Kekurangan Uji Nonparametrik
Meskipun memiliki beberapa kelebihan, uji nonparametrik juga memiliki beberapa kekurangan yang perlu dipertimbangkan:
- Kurang efisien: Uji nonparametrik umumnya kurang efisien dibandingkan dengan uji parametrik, artinya membutuhkan ukuran sampel yang lebih besar untuk mencapai tingkat signifikansi yang sama.
- Kurang kuat: Uji nonparametrik kurang kuat dalam mendeteksi perbedaan yang sebenarnya, artinya lebih sulit untuk menolak hipotesis nol ketika hipotesis alternatif benar.
- Pilihan uji terbatas: Terdapat pilihan uji nonparametrik yang lebih sedikit dibandingkan dengan uji parametrik, sehingga mungkin tidak selalu ada uji yang tepat untuk setiap situasi.
Perbandingan dengan Uji Parametrik
Perbandingan antara uji nonparametrik dan uji parametrik dapat dirangkum dalam tabel berikut:
| Kriteria | Uji Parametrik | Uji Nonparametrik |
|---|---|---|
| Asumsi Distribusi | Membutuhkan asumsi distribusi normal dan homogenitas varians | Tidak membutuhkan asumsi distribusi |
| Efisiensi | Lebih efisien | Kurang efisien |
| Kekuatan | Lebih kuat | Kurang kuat |
| Jenis Data | Interval atau rasio | Ordinal, nominal, interval, atau rasio |
| Ketahanan terhadap Outlier | Rentan terhadap outlier | Lebih tahan terhadap outlier |
Penerapan Uji Nonparametrik dalam Berbagai Bidang
Uji statistik nonparametrik menawarkan solusi yang fleksibel dan kuat dalam menganalisis data, terutama ketika asumsi uji parametrik tidak terpenuhi. Penerapannya luas, mencakup berbagai bidang seperti kesehatan, pendidikan, ekonomi, dan sosial. Uji nonparametrik memungkinkan peneliti untuk menarik kesimpulan yang bermakna dari data yang mungkin tidak mengikuti distribusi normal atau memiliki ukuran sampel yang kecil.
Penerapan dalam Bidang Kesehatan
Dalam bidang kesehatan, uji nonparametrik berperan penting dalam menganalisis data yang berhubungan dengan kondisi medis, pengobatan, dan efektivitas terapi. Uji nonparametrik membantu peneliti untuk menguji hipotesis tentang perbedaan antara kelompok pasien, menilai efektivitas pengobatan, dan mengidentifikasi faktor-faktor yang mempengaruhi hasil kesehatan.
- Uji Wilcoxon Signed-Rank digunakan untuk membandingkan dua kelompok data yang berpasangan, misalnya untuk menilai efektivitas pengobatan baru pada pasien yang sama sebelum dan sesudah pengobatan.
- Uji Mann-Whitney U digunakan untuk membandingkan dua kelompok data yang independen, misalnya untuk menguji perbedaan tingkat keparahan penyakit antara dua kelompok pasien yang menerima pengobatan yang berbeda.
- Uji Kruskal-Wallis digunakan untuk membandingkan lebih dari dua kelompok data yang independen, misalnya untuk menguji perbedaan tingkat keparahan penyakit antara tiga kelompok pasien yang menerima tiga jenis pengobatan yang berbeda.
Penerapan dalam Bidang Pendidikan
Dalam bidang pendidikan, uji nonparametrik digunakan untuk menganalisis data tentang kinerja siswa, efektivitas metode pembelajaran, dan pengaruh faktor-faktor lain terhadap hasil belajar. Uji nonparametrik membantu peneliti untuk menguji hipotesis tentang perbedaan antara kelompok siswa, menilai efektivitas metode pembelajaran, dan mengidentifikasi faktor-faktor yang mempengaruhi hasil belajar.
- Uji Friedman digunakan untuk membandingkan lebih dari dua kelompok data yang berpasangan, misalnya untuk menilai efektivitas tiga metode pembelajaran yang berbeda pada kelompok siswa yang sama.
- Uji Kolmogorov-Smirnov digunakan untuk menguji perbedaan distribusi data antara dua kelompok siswa, misalnya untuk menguji perbedaan distribusi nilai ujian antara siswa yang mengikuti program pembelajaran online dan siswa yang mengikuti program pembelajaran tatap muka.
Penerapan dalam Bidang Ekonomi
Dalam bidang ekonomi, uji nonparametrik digunakan untuk menganalisis data tentang pola konsumsi, tren pasar, dan pengaruh faktor-faktor ekonomi terhadap perilaku konsumen. Uji nonparametrik membantu peneliti untuk menguji hipotesis tentang perbedaan antara kelompok konsumen, menilai pengaruh faktor ekonomi terhadap perilaku konsumen, dan mengidentifikasi tren pasar.
- Uji Spearman Rank Correlation digunakan untuk menguji hubungan antara dua variabel yang tidak berdistribusi normal, misalnya untuk menguji hubungan antara tingkat pendapatan dan tingkat pengeluaran konsumen.
- Uji Kendall Rank Correlation digunakan untuk menguji hubungan antara dua variabel yang tidak berdistribusi normal, misalnya untuk menguji hubungan antara tingkat inflasi dan tingkat pengangguran.
Penerapan dalam Bidang Sosial
Dalam bidang sosial, uji nonparametrik digunakan untuk menganalisis data tentang perilaku sosial, sikap, dan opini publik. Uji nonparametrik membantu peneliti untuk menguji hipotesis tentang perbedaan antara kelompok sosial, menilai pengaruh faktor sosial terhadap perilaku, dan mengidentifikasi tren sosial.
- Uji Chi-Square digunakan untuk menguji hubungan antara dua variabel kategorikal, misalnya untuk menguji hubungan antara tingkat pendidikan dan tingkat partisipasi politik.
- Uji Fisher’s Exact Test digunakan untuk menguji hubungan antara dua variabel kategorikal, terutama ketika ukuran sampel kecil, misalnya untuk menguji hubungan antara jenis kelamin dan tingkat kepuasan terhadap layanan publik.
| Bidang | Contoh Penerapan | Uji Nonparametrik yang Digunakan |
|---|---|---|
| Kesehatan | Menganalisis efektivitas pengobatan baru pada pasien yang menderita penyakit jantung | Uji Wilcoxon Signed-Rank |
| Pendidikan | Menganalisis perbedaan kinerja siswa antara kelas yang menggunakan metode pembelajaran tradisional dan kelas yang menggunakan metode pembelajaran berbasis teknologi | Uji Mann-Whitney U |
| Ekonomi | Menganalisis hubungan antara tingkat pengangguran dan tingkat inflasi | Uji Spearman Rank Correlation |
| Sosial | Menganalisis hubungan antara tingkat pendidikan dan tingkat partisipasi politik | Uji Chi-Square |
Software Statistik untuk Uji Nonparametrik
Analisis statistik nonparametrik semakin populer karena kemampuannya dalam menangani data yang tidak memenuhi asumsi distribusi normal. Untuk membantu peneliti dalam melakukan uji nonparametrik, beberapa software statistik telah dikembangkan dengan fitur yang dirancang khusus untuk analisis ini. Berikut adalah beberapa software statistik yang dapat digunakan untuk melakukan uji statistik nonparametrik.
Software Statistik untuk Uji Nonparametrik
Software statistik untuk uji nonparametrik menyediakan berbagai fitur yang memudahkan peneliti dalam melakukan analisis data. Beberapa fitur yang umumnya tersedia dalam software ini meliputi:
- Uji Nonparametrik Umum: Software ini menyediakan berbagai uji nonparametrik seperti uji Wilcoxon, uji Mann-Whitney, uji Kruskal-Wallis, uji Friedman, uji run, uji Kolmogorov-Smirnov, dan uji chi-square.
- Visualisasi Data: Fitur visualisasi data memungkinkan peneliti untuk melihat pola dan tren dalam data, sehingga membantu dalam memahami data sebelum melakukan uji statistik.
- Pembuatan Tabel dan Grafik: Software ini memungkinkan peneliti untuk membuat tabel dan grafik yang diperlukan untuk melaporkan hasil analisis.
- Dokumentasi dan Laporan: Fitur ini membantu peneliti dalam mendokumentasikan hasil analisis dan membuat laporan yang mudah dipahami.
- Dukungan Bahasa Pemrograman: Beberapa software statistik memungkinkan peneliti untuk melakukan analisis dengan menggunakan bahasa pemrograman seperti R atau Python, sehingga memberikan fleksibilitas yang lebih besar.
Perbandingan Software Statistik
Berikut adalah tabel yang membandingkan beberapa software statistik yang populer untuk analisis nonparametrik:
| Software | Fitur Utama | Kelebihan | Kekurangan |
|---|---|---|---|
| SPSS | – Uji nonparametrik umum – Visualisasi data – Pembuatan tabel dan grafik – Dokumentasi dan laporan |
– Antarmuka yang mudah digunakan – Fitur lengkap – Dukungan yang luas |
– Harga yang mahal – Tidak fleksibel untuk analisis yang lebih kompleks |
| R | – Uji nonparametrik umum – Visualisasi data yang canggih – Fleksibilitas dalam analisis |
– Gratis dan open-source – Fleksibilitas yang tinggi – Komunitas pengguna yang besar |
– Kurva pembelajaran yang lebih curam – Antarmuka yang kurang ramah pengguna |
| Stata | – Uji nonparametrik umum – Visualisasi data – Pembuatan tabel dan grafik |
– Antarmuka yang ramah pengguna – Fitur yang kuat untuk analisis data |
– Harga yang mahal – Tidak sefleksibel R |
| JMP | – Uji nonparametrik umum – Visualisasi data interaktif – Analisis eksplorasi data |
– Antarmuka yang interaktif – Fitur visualisasi yang kuat – Analisis yang terintegrasi |
– Harga yang mahal – Kurang fleksibel untuk analisis yang lebih kompleks |
Akhir Kata
Melalui contoh soal yang telah kita bahas, Anda telah mempelajari bagaimana statistik nonparametrik dapat digunakan untuk menganalisis data tanpa asumsi distribusi tertentu. Kemampuan untuk menguji hipotesis dengan data yang tidak terdistribusi normal menjadikan statistik nonparametrik alat yang ampuh dalam berbagai bidang. Jangan ragu untuk menjelajahi lebih dalam dan mengasah kemampuan Anda dalam mengaplikasikan teknik ini dalam berbagai situasi penelitian.




