Contoh soal statistik parametrik dan nonparametrik – Statistik parametrik dan nonparametrik adalah dua pendekatan utama dalam analisis data, masing-masing memiliki kekuatan dan kelemahan tersendiri. Dalam dunia penelitian, memahami perbedaan dan penerapan kedua pendekatan ini sangat penting untuk menghasilkan kesimpulan yang akurat dan valid.
Artikel ini akan membahas contoh soal statistik parametrik dan nonparametrik, memberikan pemahaman mendalam tentang kedua pendekatan ini, mulai dari asumsi dasar hingga contoh penerapan dalam berbagai bidang. Dengan memahami kedua pendekatan ini, Anda dapat memilih metode analisis yang tepat untuk data Anda dan menghasilkan interpretasi yang lebih baik.
Pengenalan Statistik Parametrik dan Nonparametrik
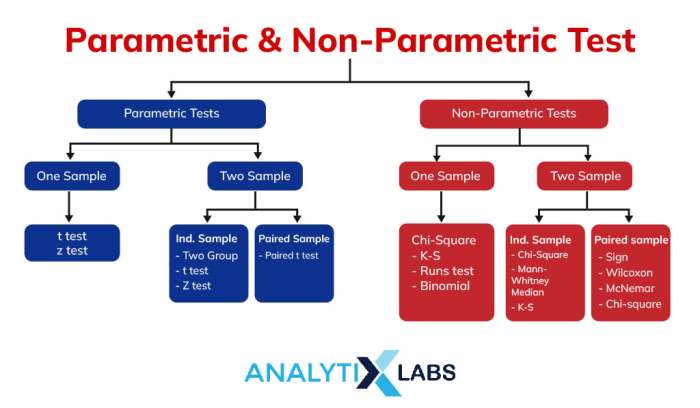
Dalam dunia statistik, terdapat dua pendekatan utama untuk menganalisis data: statistik parametrik dan nonparametrik. Kedua pendekatan ini memiliki perbedaan mendasar dalam asumsi yang mereka gunakan dan jenis data yang mereka tangani. Memahami perbedaan ini sangat penting untuk memilih metode analisis yang tepat untuk penelitian Anda.
Perbedaan Statistik Parametrik dan Nonparametrik
Perbedaan utama antara statistik parametrik dan nonparametrik terletak pada asumsi yang mereka gunakan tentang populasi data. Statistik parametrik mengasumsikan bahwa data berasal dari distribusi tertentu, seperti distribusi normal, dan bahwa parameter populasi (misalnya, rata-rata dan standar deviasi) diketahui atau dapat diestimasi. Statistik nonparametrik, di sisi lain, tidak membuat asumsi tentang distribusi populasi dan parameternya.
Contoh Penerapan Statistik Parametrik dan Nonparametrik
Berikut adalah beberapa contoh penerapan statistik parametrik dan nonparametrik dalam berbagai bidang:
- Statistik Parametrik
- Ilmu Kesehatan: Uji t untuk membandingkan rata-rata tekanan darah antara dua kelompok pasien.
- Bisnis: Analisis regresi linier untuk memprediksi penjualan berdasarkan pengeluaran iklan.
- Pendidikan: Analisis varians (ANOVA) untuk membandingkan kinerja siswa dalam tiga metode pembelajaran yang berbeda.
- Statistik Nonparametrik
- Ilmu Sosial: Uji Mann-Whitney untuk membandingkan preferensi konsumen terhadap dua merek produk.
- Biologi: Uji Kruskal-Wallis untuk membandingkan tingkat pertumbuhan tanaman dalam tiga kondisi tanah yang berbeda.
- Psikologi: Uji Wilcoxon untuk membandingkan tingkat stres sebelum dan sesudah intervensi terapi.
Karakteristik Data untuk Analisis Statistik Parametrik dan Nonparametrik
Jenis data yang cocok untuk analisis statistik parametrik dan nonparametrik berbeda. Berikut adalah karakteristik data yang ideal untuk masing-masing pendekatan:
Data untuk Analisis Statistik Parametrik
- Data harus terdistribusi normal atau setidaknya mendekati normal.
- Data harus bersifat interval atau rasio.
- Data harus bebas dari outlier yang signifikan.
- Ukuran sampel harus cukup besar (biasanya lebih dari 30).
Data untuk Analisis Statistik Nonparametrik
- Tidak ada asumsi tentang distribusi data.
- Data dapat bersifat ordinal, interval, atau rasio.
- Data dapat memiliki outlier yang signifikan.
- Ukuran sampel dapat kecil atau besar.
Asumsi Statistik Parametrik
Statistik parametrik adalah cabang statistik yang mengandalkan asumsi-asumsi tertentu tentang distribusi data. Asumsi-asumsi ini penting karena memengaruhi validitas dan reliabilitas hasil analisis statistik. Jika asumsi-asumsi ini tidak terpenuhi, hasil analisis statistik parametrik mungkin tidak akurat dan dapat menyesatkan. Artikel ini akan membahas asumsi-asumsi utama dalam statistik parametrik, dampak pelanggaran asumsi, dan bagaimana menguji asumsi normalitas data.
Asumsi-Asumsi Statistik Parametrik
Berikut adalah asumsi-asumsi utama yang harus dipenuhi dalam statistik parametrik:
- Data harus terdistribusi normal. Asumsi ini berarti bahwa data harus mengikuti distribusi normal, yang berbentuk lonceng. Distribusi normal memiliki rata-rata (mean) dan deviasi standar (standard deviation) yang tertentu.
- Varians data harus sama di semua kelompok. Asumsi ini, yang juga dikenal sebagai homoskedastisitas, berarti bahwa varians data harus sama di semua kelompok yang dibandingkan. Jika varians tidak sama, hasil analisis statistik parametrik dapat dipengaruhi.
- Data harus independen. Asumsi ini berarti bahwa data harus independen satu sama lain. Artinya, nilai satu data tidak boleh memengaruhi nilai data lainnya.
- Data harus berskala interval atau rasio. Asumsi ini berarti bahwa data harus diukur pada skala interval atau rasio. Skala interval memiliki jarak yang sama antara nilai-nilai, sementara skala rasio memiliki titik nol absolut.
Uji Shapiro-Wilk untuk Asumsi Normalitas
Uji Shapiro-Wilk adalah salah satu uji yang umum digunakan untuk menguji asumsi normalitas data. Uji ini menguji hipotesis nol bahwa data terdistribusi normal. Jika nilai p dari uji Shapiro-Wilk kurang dari 0,05, maka hipotesis nol ditolak, yang berarti bahwa data tidak terdistribusi normal. Sebaliknya, jika nilai p lebih besar dari 0,05, maka hipotesis nol tidak ditolak, yang berarti bahwa data mungkin terdistribusi normal.
Sebagai contoh, jika kita ingin menguji apakah data tinggi badan siswa terdistribusi normal, kita dapat menggunakan uji Shapiro-Wilk. Jika nilai p dari uji Shapiro-Wilk kurang dari 0,05, maka kita dapat menyimpulkan bahwa data tinggi badan siswa tidak terdistribusi normal.
Dampak Pelanggaran Asumsi
Pelanggaran asumsi dalam statistik parametrik dapat memiliki dampak yang signifikan pada hasil analisis statistik. Berikut adalah beberapa dampak yang mungkin terjadi:
- Hasil analisis statistik parametrik mungkin tidak akurat. Jika asumsi tidak terpenuhi, hasil analisis statistik parametrik mungkin tidak akurat. Hal ini dapat menyebabkan kesimpulan yang salah.
- Hasil analisis statistik parametrik mungkin tidak reliabel. Jika asumsi tidak terpenuhi, hasil analisis statistik parametrik mungkin tidak reliabel. Hal ini dapat menyebabkan hasil yang berbeda jika analisis dilakukan berulang kali dengan data yang sama.
- Hasil analisis statistik parametrik mungkin tidak valid. Jika asumsi tidak terpenuhi, hasil analisis statistik parametrik mungkin tidak valid. Hal ini berarti bahwa hasil analisis tidak dapat digeneralisasikan ke populasi yang lebih besar.
Jenis-Jenis Uji Statistik Parametrik
Uji statistik parametrik merupakan metode analisis data yang didasarkan pada asumsi distribusi data tertentu, seperti distribusi normal. Jenis uji ini umumnya digunakan untuk menganalisis data kuantitatif, seperti data numerik, yang memenuhi syarat tertentu, seperti data terdistribusi normal, varians sama, dan skala pengukuran interval atau rasio.
Dalam praktiknya, ada beberapa jenis uji statistik parametrik yang dapat digunakan, masing-masing memiliki keunggulan dan kelemahan tersendiri.
Jenis-Jenis Uji Statistik Parametrik
Berikut adalah tabel yang merangkum beberapa jenis uji statistik parametrik dan contoh penerapannya:
| Jenis Uji | Tujuan | Contoh Penerapan |
|---|---|---|
| Uji t-test | Membandingkan rata-rata dua kelompok data | Membandingkan efektivitas dua jenis obat dalam menurunkan tekanan darah |
| Uji ANOVA | Membandingkan rata-rata lebih dari dua kelompok data | Membandingkan efektivitas tiga metode pembelajaran terhadap hasil belajar siswa |
| Uji Regresi Linear | Menganalisis hubungan linear antara dua variabel | Menganalisis hubungan antara jumlah jam belajar dan nilai ujian mahasiswa |
| Uji Korelasi | Menganalisis kekuatan dan arah hubungan antara dua variabel | Menganalisis hubungan antara tinggi badan dan berat badan |
Uji Statistik Parametrik untuk Membandingkan Rata-Rata Dua Kelompok Data
Uji statistik parametrik yang paling umum digunakan untuk menguji perbedaan rata-rata dua kelompok data adalah uji t-test. Uji ini memiliki beberapa variasi, yaitu uji t-test untuk data independen (independent samples t-test) dan uji t-test untuk data berpasangan (paired samples t-test). Uji t-test untuk data independen digunakan untuk membandingkan rata-rata dua kelompok data yang tidak saling berhubungan, sedangkan uji t-test untuk data berpasangan digunakan untuk membandingkan rata-rata dua kelompok data yang saling berhubungan.
Langkah-Langkah Pengujian Hipotesis dengan Uji t-test untuk Data Berpasangan
Langkah-langkah pengujian hipotesis dengan uji t-test untuk data berpasangan adalah sebagai berikut:
- Merumuskan hipotesis nol (H0) dan hipotesis alternatif (H1).
- Menentukan tingkat signifikansi (α).
- Menghitung statistik uji t.
- Menentukan nilai p.
- Membuat keputusan.
Sebagai contoh, misalkan kita ingin menguji apakah ada perbedaan rata-rata tekanan darah sebelum dan sesudah mengonsumsi obat tertentu. Hipotesis nol (H0) adalah tidak ada perbedaan rata-rata tekanan darah sebelum dan sesudah mengonsumsi obat, sedangkan hipotesis alternatif (H1) adalah ada perbedaan rata-rata tekanan darah sebelum dan sesudah mengonsumsi obat. Tingkat signifikansi (α) dapat ditentukan sebesar 0.05. Kemudian, kita dapat menghitung statistik uji t menggunakan rumus:
t = (rata-rata selisih) / (standar deviasi selisih / akar kuadrat dari jumlah pasangan)
Nilai p dapat diperoleh dari tabel distribusi t atau menggunakan software statistik. Jika nilai p lebih kecil dari tingkat signifikansi (α), maka hipotesis nol ditolak. Artinya, terdapat perbedaan rata-rata tekanan darah sebelum dan sesudah mengonsumsi obat. Sebaliknya, jika nilai p lebih besar dari tingkat signifikansi (α), maka hipotesis nol diterima. Artinya, tidak terdapat perbedaan rata-rata tekanan darah sebelum dan sesudah mengonsumsi obat.
Contoh Soal Statistik Parametrik
Setelah membahas statistik nonparametrik, kita akan menjelajahi contoh soal statistik parametrik. Statistik parametrik mengasumsikan bahwa data mengikuti distribusi tertentu, seperti distribusi normal. Metode ini digunakan untuk menganalisis data kuantitatif dan sering digunakan dalam penelitian ilmiah. Beberapa contoh teknik statistik parametrik meliputi uji t-test, ANOVA, dan uji korelasi Pearson.
Uji t-test untuk Data Independen
Uji t-test untuk data independen digunakan untuk membandingkan rata-rata dua kelompok independen. Misalkan kita ingin mengetahui apakah ada perbedaan signifikan dalam skor ujian antara siswa yang mengikuti program pembelajaran online dan siswa yang mengikuti pembelajaran tatap muka.
- Contoh Soal: Dua kelompok siswa, masing-masing berjumlah 20 orang, diberikan dua metode pembelajaran yang berbeda: online dan tatap muka. Setelah mengikuti program pembelajaran, mereka diberikan tes akhir. Skor ujian kedua kelompok dicatat. Kita ingin mengetahui apakah ada perbedaan signifikan dalam skor ujian antara kedua kelompok.
- Penyelesaian: Kita dapat menggunakan uji t-test independen untuk menganalisis data. Hipotesis nol menyatakan bahwa tidak ada perbedaan signifikan dalam skor ujian antara kedua kelompok, sedangkan hipotesis alternatif menyatakan bahwa ada perbedaan signifikan. Dengan menggunakan software statistik, kita dapat menghitung nilai p. Jika nilai p kurang dari tingkat signifikansi (misalnya, 0.05), kita tolak hipotesis nol dan simpulkan bahwa ada perbedaan signifikan dalam skor ujian antara kedua kelompok.
Uji ANOVA Satu Arah
Uji ANOVA (Analysis of Variance) satu arah digunakan untuk membandingkan rata-rata dari tiga atau lebih kelompok. Misalnya, kita ingin mengetahui apakah ada perbedaan signifikan dalam tingkat kepuasan pelanggan terhadap tiga merek produk yang berbeda.
- Contoh Soal: Sebuah perusahaan ingin mengetahui apakah ada perbedaan signifikan dalam tingkat kepuasan pelanggan terhadap tiga merek produk yang berbeda. Mereka melakukan survei kepada 100 pelanggan, masing-masing 33 pelanggan untuk setiap merek. Data survei menunjukkan skor kepuasan pelanggan untuk setiap merek.
- Penyelesaian: Kita dapat menggunakan uji ANOVA satu arah untuk menganalisis data. Hipotesis nol menyatakan bahwa tidak ada perbedaan signifikan dalam tingkat kepuasan pelanggan antara ketiga merek, sedangkan hipotesis alternatif menyatakan bahwa ada perbedaan signifikan. Dengan menggunakan software statistik, kita dapat menghitung nilai p. Jika nilai p kurang dari tingkat signifikansi (misalnya, 0.05), kita tolak hipotesis nol dan simpulkan bahwa ada perbedaan signifikan dalam tingkat kepuasan pelanggan antara ketiga merek.
Uji Korelasi Pearson
Uji korelasi Pearson digunakan untuk mengukur hubungan linear antara dua variabel kontinu. Misalnya, kita ingin mengetahui apakah ada hubungan linear antara jumlah jam belajar dan nilai ujian siswa.
- Contoh Soal: Seorang guru ingin mengetahui apakah ada hubungan linear antara jumlah jam belajar dan nilai ujian siswa. Dia mengumpulkan data tentang jumlah jam belajar dan nilai ujian dari 50 siswa.
- Penyelesaian: Kita dapat menggunakan uji korelasi Pearson untuk menganalisis data. Koefisien korelasi Pearson (r) menunjukkan kekuatan dan arah hubungan linear antara dua variabel. Nilai r berkisar antara -1 hingga 1. Nilai r positif menunjukkan hubungan positif, nilai r negatif menunjukkan hubungan negatif, dan nilai r 0 menunjukkan tidak ada hubungan linear. Dengan menggunakan software statistik, kita dapat menghitung koefisien korelasi Pearson dan nilai p. Jika nilai p kurang dari tingkat signifikansi (misalnya, 0.05), kita tolak hipotesis nol dan simpulkan bahwa ada hubungan linear signifikan antara jumlah jam belajar dan nilai ujian siswa.
Jenis-Jenis Uji Statistik Nonparametrik
Uji statistik nonparametrik merupakan metode pengujian hipotesis yang tidak memerlukan asumsi distribusi data tertentu. Ini sangat berguna ketika data tidak mengikuti distribusi normal, seperti distribusi normal atau distribusi t, atau ketika skala pengukuran data adalah ordinal atau nominal. Dalam konteks ini, uji nonparametrik menawarkan alternatif yang kuat dan fleksibel untuk analisis data.
Jenis-Jenis Uji Statistik Nonparametrik
Uji statistik nonparametrik memiliki berbagai jenis, masing-masing dirancang untuk menjawab pertanyaan spesifik terkait data. Berikut tabel yang merangkum jenis-jenis uji statistik nonparametrik beserta contoh penerapannya:
| Jenis Uji | Tujuan | Contoh Penerapan |
|---|---|---|
| Uji Wilcoxon Signed-Rank | Membandingkan dua kelompok data berpasangan (dependent) | Membandingkan tingkat kepuasan pelanggan sebelum dan sesudah program pelatihan baru diterapkan. |
| Uji Mann-Whitney U | Membandingkan dua kelompok data independen | Membandingkan efektivitas dua jenis obat dalam mengobati penyakit tertentu. |
| Uji Kruskal-Wallis | Membandingkan lebih dari dua kelompok data independen | Membandingkan kinerja siswa dari tiga sekolah yang berbeda pada ujian nasional. |
| Uji Friedman | Membandingkan lebih dari dua kelompok data berpasangan (dependent) | Membandingkan efektivitas tiga metode pembelajaran yang berbeda pada kelompok siswa yang sama. |
| Uji Chi-Square | Menguji hubungan antara dua variabel kategorikal | Menguji apakah ada hubungan antara jenis kelamin dan preferensi merek mobil. |
| Uji Run | Menguji apakah data bersifat acak atau tidak | Menguji apakah hasil lemparan koin benar-benar acak. |
Uji Statistik Nonparametrik untuk Membandingkan Median Dua Kelompok Data
Untuk menguji perbedaan median dua kelompok data independen, uji Mann-Whitney U merupakan pilihan yang tepat. Uji ini mengasumsikan bahwa data dalam kedua kelompok berasal dari populasi yang sama, tetapi tidak memerlukan asumsi distribusi normal. Uji ini membandingkan peringkat data dari kedua kelompok, bukan nilai data mentahnya.
Langkah-Langkah Pengujian Hipotesis dengan Uji Mann-Whitney U untuk Data Independen
Langkah-langkah pengujian hipotesis dengan uji Mann-Whitney U untuk data independen adalah sebagai berikut:
- Rumuskan Hipotesis
- Hipotesis Nol (H0): Tidak ada perbedaan median antara kedua kelompok data.
- Hipotesis Alternatif (H1): Ada perbedaan median antara kedua kelompok data.
- Tentukan Tingkat Signifikansi (α)
Tingkat signifikansi (α) adalah probabilitas menolak hipotesis nol ketika sebenarnya benar. Nilai α yang umum digunakan adalah 0,05.
- Hitung Statistik Uji
Statistik uji Mann-Whitney U dihitung dengan menggunakan rumus:
U = n1n2 + n1(n1+1)/2 – R1
di mana:
- n1 adalah ukuran sampel kelompok pertama
- n2 adalah ukuran sampel kelompok kedua
- R1 adalah jumlah peringkat data dalam kelompok pertama
- Tentukan Nilai Kritikal
Nilai kritikal untuk uji Mann-Whitney U dapat ditemukan dalam tabel distribusi Mann-Whitney U. Nilai kritikal ini bergantung pada tingkat signifikansi (α) dan ukuran sampel kedua kelompok.
- Buat Keputusan
Jika statistik uji lebih kecil dari nilai kritikal, tolak hipotesis nol. Jika statistik uji lebih besar dari nilai kritikal, gagal menolak hipotesis nol.
- Interpretasikan Hasil
Interpretasikan hasil pengujian berdasarkan keputusan yang diambil. Jika hipotesis nol ditolak, berarti ada perbedaan median yang signifikan antara kedua kelompok data. Jika hipotesis nol gagal ditolak, berarti tidak ada bukti yang cukup untuk menyimpulkan adanya perbedaan median yang signifikan.
Contoh Soal Statistik Nonparametrik: Contoh Soal Statistik Parametrik Dan Nonparametrik
Statistik nonparametrik merupakan cabang statistik yang tidak bergantung pada asumsi distribusi data tertentu. Metode ini sangat berguna ketika data tidak memenuhi asumsi normalitas atau ketika skala pengukuran data bersifat ordinal atau nominal. Dalam contoh soal berikut, kita akan membahas beberapa uji statistik nonparametrik yang umum digunakan.
Uji Wilcoxon Signed-Rank Test
Uji Wilcoxon signed-rank test merupakan uji nonparametrik yang digunakan untuk membandingkan dua kelompok data berpasangan. Uji ini mengasumsikan bahwa data berpasangan dan memiliki distribusi simetris.
- Contoh Soal: Seorang peneliti ingin mengetahui apakah ada perbedaan yang signifikan dalam skor motivasi sebelum dan sesudah mengikuti program pelatihan motivasi. Data berikut menunjukkan skor motivasi dari 10 peserta:
| Peserta | Skor Sebelum | Skor Sesudah |
|---|---|---|
| 1 | 5 | 7 |
| 2 | 6 | 8 |
| 3 | 4 | 6 |
| 4 | 7 | 9 |
| 5 | 8 | 10 |
| 6 | 3 | 5 |
| 7 | 9 | 11 |
| 8 | 2 | 4 |
| 9 | 10 | 12 |
| 10 | 1 | 3 |
- Penyelesaian:
- Hitung selisih skor sebelum dan sesudah untuk setiap peserta.
- Urutkan selisih skor dari yang terkecil hingga terbesar, tanpa memperhatikan tanda.
- Berikan peringkat pada setiap selisih skor, mulai dari peringkat 1 untuk selisih terkecil.
- Hitung jumlah peringkat untuk selisih skor positif (T+) dan jumlah peringkat untuk selisih skor negatif (T-).
- Tentukan statistik uji Wilcoxon signed-rank (W) sebagai nilai T+ atau T- yang lebih kecil.
- Bandingkan statistik uji dengan nilai kritis Wilcoxon signed-rank test dengan derajat kebebasan (n-1) dan tingkat signifikansi (α) yang ditentukan.
- Jika statistik uji lebih kecil dari nilai kritis, maka tolak hipotesis nol bahwa tidak ada perbedaan yang signifikan dalam skor motivasi sebelum dan sesudah program pelatihan.
Uji Kruskal-Wallis
Uji Kruskal-Wallis merupakan uji nonparametrik yang digunakan untuk menguji perbedaan median lebih dari dua kelompok data. Uji ini mengasumsikan bahwa data berasal dari populasi yang memiliki distribusi yang sama, tetapi tidak perlu berdistribusi normal.
- Contoh Soal: Seorang peneliti ingin mengetahui apakah ada perbedaan yang signifikan dalam tingkat kepuasan pelanggan di antara tiga jenis layanan pelanggan: telepon, email, dan chat online. Data berikut menunjukkan skor kepuasan pelanggan dari 15 pelanggan:
| Layanan | Skor Kepuasan |
|---|---|
| Telepon | 7 |
| Telepon | 8 |
| Telepon | 9 |
| 6 | |
| 5 | |
| 4 | |
| Chat Online | 10 |
| Chat Online | 11 |
| Chat Online | 12 |
| Telepon | 6 |
| 3 | |
| Chat Online | 9 |
| Telepon | 5 |
| 7 | |
| Chat Online | 8 |
- Penyelesaian:
- Gabungkan semua data dari ketiga kelompok dan urutkan dari yang terkecil hingga terbesar.
- Berikan peringkat pada setiap data, mulai dari peringkat 1 untuk data terkecil.
- Hitung jumlah peringkat untuk setiap kelompok.
- Tentukan statistik uji Kruskal-Wallis (H) dengan rumus:
H = [(12/(N(N+1)) * Σ(Ri2/ni)] – 3(N+1)
- Dimana:
- N = Jumlah total data
- Ri = Jumlah peringkat untuk kelompok i
- ni = Jumlah data untuk kelompok i
- Bandingkan statistik uji dengan nilai kritis Kruskal-Wallis test dengan derajat kebebasan (k-1) dan tingkat signifikansi (α) yang ditentukan.
- Jika statistik uji lebih besar dari nilai kritis, maka tolak hipotesis nol bahwa tidak ada perbedaan yang signifikan dalam tingkat kepuasan pelanggan di antara ketiga jenis layanan pelanggan.
Uji Spearman Rank Correlation
Uji Spearman rank correlation merupakan uji nonparametrik yang digunakan untuk mengukur hubungan non-linear antara dua variabel. Uji ini mengasumsikan bahwa data berpasangan dan memiliki distribusi ordinal atau interval.
Contoh soal statistik parametrik dan nonparametrik seringkali melibatkan pengujian hipotesis dan analisis data. Misalnya, kita bisa menggunakan uji t untuk membandingkan rata-rata dua kelompok data. Nah, berbicara soal analisis data, kita juga bisa melihat contoh soal mengenai perhitungan daya dukung tanah untuk pondasi dangkal.
Contoh soal pondasi dangkal ini dapat membantu kita memahami bagaimana menentukan ukuran pondasi yang tepat berdasarkan jenis tanah dan beban bangunan. Dengan demikian, mempelajari contoh soal statistik dan contoh soal pondasi dangkal dapat membantu kita dalam memahami berbagai konsep penting di bidang teknik dan ilmu data.
- Contoh Soal: Seorang peneliti ingin mengetahui apakah ada hubungan antara tingkat motivasi karyawan dengan kinerja mereka. Data berikut menunjukkan tingkat motivasi dan kinerja dari 10 karyawan:
| Karyawan | Tingkat Motivasi | Kinerja |
|---|---|---|
| 1 | 7 | 8 |
| 2 | 5 | 6 |
| 3 | 9 | 10 |
| 4 | 3 | 4 |
| 5 | 6 | 7 |
| 6 | 8 | 9 |
| 7 | 2 | 3 |
| 8 | 4 | 5 |
| 9 | 10 | 11 |
| 10 | 1 | 2 |
- Penyelesaian:
- Urutkan data tingkat motivasi dan kinerja dari yang terkecil hingga terbesar.
- Berikan peringkat pada setiap data, mulai dari peringkat 1 untuk data terkecil.
- Hitung selisih peringkat (d) untuk setiap pasangan data.
- Kuadratkan setiap selisih peringkat (d2).
- Tentukan statistik uji Spearman rank correlation (rs) dengan rumus:
rs = 1 – [(6 * Σd2) / (n(n2-1))]
- Dimana:
- n = Jumlah data
- Σd2 = Jumlah kuadrat selisih peringkat
- Bandingkan statistik uji dengan nilai kritis Spearman rank correlation test dengan derajat kebebasan (n-2) dan tingkat signifikansi (α) yang ditentukan.
- Jika statistik uji lebih besar dari nilai kritis, maka tolak hipotesis nol bahwa tidak ada hubungan yang signifikan antara tingkat motivasi karyawan dengan kinerja mereka.
Perbandingan Statistik Parametrik dan Nonparametrik
Dalam analisis data, pemilihan jenis uji statistik yang tepat sangat penting untuk memperoleh hasil yang akurat dan bermakna. Dua pendekatan utama dalam pengujian statistik adalah statistik parametrik dan nonparametrik. Kedua pendekatan ini memiliki keunggulan dan kelemahan masing-masing, sehingga pemilihannya bergantung pada karakteristik data dan tujuan penelitian.
Perbandingan Keunggulan dan Kelemahan
Berikut adalah tabel yang membandingkan keunggulan dan kelemahan statistik parametrik dan nonparametrik:
| Aspek | Statistik Parametrik | Statistik Nonparametrik |
|---|---|---|
| Asumsi Data | Membutuhkan asumsi tentang distribusi data, seperti distribusi normal. | Tidak memerlukan asumsi distribusi data. |
| Keunggulan |
|
|
| Kelemahan |
|
|
Faktor-faktor yang Perlu Dipertimbangkan dalam Memilih Jenis Uji Statistik
Berikut adalah beberapa faktor yang perlu dipertimbangkan dalam memilih jenis uji statistik yang tepat:
- Jenis data: Apakah data kontinu, diskrit, ordinal, atau nominal?
- Ukuran sampel: Apakah ukuran sampel besar atau kecil?
- Distribusi data: Apakah data terdistribusi normal atau tidak normal?
- Tujuan penelitian: Apakah ingin menguji perbedaan, hubungan, atau memprediksi?
Contoh Kasus di Mana Statistik Nonparametrik Lebih Disukai
Statistik nonparametrik lebih disukai dalam kasus-kasus di mana asumsi distribusi data tidak terpenuhi atau ukuran sampel kecil. Berikut adalah beberapa contoh:
- Data ordinal: Misalnya, dalam survei kepuasan pelanggan, data yang dikumpulkan mungkin berupa skala ordinal (sangat puas, puas, netral, tidak puas, sangat tidak puas). Statistik nonparametrik, seperti uji Wilcoxon, dapat digunakan untuk menganalisis data ordinal ini.
- Data dengan outlier: Outlier dapat memengaruhi hasil uji statistik parametrik. Statistik nonparametrik, seperti uji Mann-Whitney, lebih tahan terhadap outlier dan dapat memberikan hasil yang lebih akurat.
- Ukuran sampel kecil: Statistik parametrik membutuhkan ukuran sampel yang cukup besar untuk memberikan hasil yang valid. Statistik nonparametrik, seperti uji Kruskal-Wallis, dapat digunakan untuk menganalisis data dengan ukuran sampel kecil.
Aplikasi Statistik Parametrik dan Nonparametrik dalam Riset
Dalam dunia penelitian, pemilihan metode statistik yang tepat sangatlah penting untuk mendapatkan hasil yang akurat dan dapat diandalkan. Statistik parametrik dan nonparametrik menawarkan pendekatan yang berbeda dalam menganalisis data, masing-masing memiliki keunggulan dan keterbatasannya sendiri. Memahami perbedaan dan penerapan kedua jenis statistik ini sangatlah penting bagi para peneliti untuk memilih metode yang paling sesuai dengan data dan pertanyaan penelitian mereka.
Penerapan Statistik Parametrik dan Nonparametrik dalam Penelitian Kesehatan
Dalam bidang kesehatan, statistik parametrik dan nonparametrik memiliki peran penting dalam berbagai penelitian. Berikut adalah contoh penerapannya:
- Statistik Parametrik sering digunakan dalam penelitian klinis untuk membandingkan efektivitas dua jenis pengobatan. Misalnya, peneliti dapat menggunakan uji t-student untuk membandingkan rata-rata tekanan darah pasien yang menerima pengobatan A dengan pasien yang menerima pengobatan B. Asumsi utama dalam statistik parametrik adalah data berdistribusi normal, yang sering kali terpenuhi dalam penelitian kesehatan.
- Statistik Nonparametrik, di sisi lain, lebih fleksibel dan tidak memerlukan asumsi distribusi data tertentu. Contohnya, peneliti dapat menggunakan uji Mann-Whitney U untuk membandingkan tingkat kepuasan pasien terhadap dua jenis layanan kesehatan, tanpa harus mengasumsikan data berdistribusi normal.
Penggunaan Statistik Parametrik dan Nonparametrik dalam Analisis Data Survei
Data survei seringkali digunakan untuk mengumpulkan informasi dari populasi yang luas. Statistik parametrik dan nonparametrik dapat membantu peneliti dalam menganalisis data survei dan menarik kesimpulan yang bermakna.
- Statistik Parametrik dapat digunakan untuk menganalisis data survei yang memenuhi asumsi distribusi normal. Misalnya, peneliti dapat menggunakan analisis regresi linear untuk memprediksi tingkat kepuasan pelanggan terhadap suatu produk berdasarkan faktor-faktor seperti usia, jenis kelamin, dan pendapatan.
- Statistik Nonparametrik sangat berguna dalam menganalisis data survei yang tidak memenuhi asumsi distribusi normal atau memiliki data ordinal. Misalnya, peneliti dapat menggunakan uji Kruskal-Wallis untuk membandingkan tingkat kepuasan pelanggan terhadap tiga jenis produk yang berbeda, tanpa harus mengasumsikan data berdistribusi normal.
Studi Kasus: Penerapan Statistik Parametrik dan Nonparametrik dalam Penelitian Kesehatan
Berikut adalah contoh studi kasus yang menggambarkan penerapan statistik parametrik dan nonparametrik dalam penelitian kesehatan:
- Studi Kasus 1: Pengaruh Olahraga Terhadap Tekanan Darah
- Studi Kasus 2: Kepuasan Pasien Terhadap Layanan Kesehatan
Peneliti ingin mengetahui pengaruh olahraga terhadap tekanan darah pada individu dengan hipertensi ringan. Mereka mengumpulkan data tekanan darah dari 50 peserta yang dibagi menjadi dua kelompok: kelompok kontrol (tidak berolahraga) dan kelompok intervensi (berolahraga secara teratur). Setelah beberapa minggu, peneliti mengukur tekanan darah kedua kelompok.
Untuk menganalisis data, peneliti dapat menggunakan uji t-student (statistik parametrik) untuk membandingkan rata-rata tekanan darah kedua kelompok. Asumsi uji t-student adalah data berdistribusi normal, yang dapat diuji dengan menggunakan uji normalitas. Jika data tidak berdistribusi normal, peneliti dapat menggunakan uji Mann-Whitney U (statistik nonparametrik) untuk membandingkan tekanan darah kedua kelompok.
Peneliti ingin mengetahui tingkat kepuasan pasien terhadap dua jenis layanan kesehatan: layanan A dan layanan B. Mereka mengumpulkan data dari 100 pasien yang telah menggunakan kedua layanan tersebut. Data yang dikumpulkan berupa skala Likert yang mengukur tingkat kepuasan pasien terhadap berbagai aspek layanan, seperti kualitas pelayanan, waktu tunggu, dan keramahan staf.
Untuk menganalisis data, peneliti dapat menggunakan uji t-student (statistik parametrik) untuk membandingkan rata-rata tingkat kepuasan pasien terhadap kedua layanan. Namun, jika data tidak berdistribusi normal, peneliti dapat menggunakan uji Wilcoxon rank-sum (statistik nonparametrik) untuk membandingkan tingkat kepuasan pasien terhadap kedua layanan.
Pentingnya Memahami Asumsi Statistik
Dalam dunia statistik, asumsi adalah pondasi yang mendasari validitas dan reliabilitas analisis data. Memahami asumsi statistik sebelum melakukan analisis data sangat penting karena asumsi ini menentukan metode statistik yang tepat untuk digunakan dan interpretasi hasil yang diperoleh. Jika asumsi statistik dilanggar, kesimpulan yang diambil dari analisis data dapat menjadi tidak akurat, menyesatkan, dan tidak dapat diandalkan.
Konsekuensi Pelanggaran Asumsi Statistik, Contoh soal statistik parametrik dan nonparametrik
Pelanggaran asumsi statistik dapat berdampak serius pada hasil analisis data. Berikut adalah beberapa konsekuensi yang mungkin terjadi:
- Hasil Analisis yang Tidak Akurat: Pelanggaran asumsi dapat menyebabkan hasil analisis yang tidak akurat dan tidak dapat diandalkan. Ini dapat mengarah pada kesimpulan yang salah dan keputusan yang tidak tepat.
- Tingkat Kesalahan yang Tinggi: Pelanggaran asumsi dapat menyebabkan tingkat kesalahan yang tinggi dalam analisis data. Hal ini dapat menyebabkan kesimpulan yang salah dan keputusan yang tidak tepat.
- Penafsiran yang Salah: Pelanggaran asumsi dapat menyebabkan penafsiran yang salah terhadap hasil analisis data. Ini dapat menyebabkan kesimpulan yang tidak tepat dan keputusan yang tidak tepat.
- Kehilangan Daya Statistik: Pelanggaran asumsi dapat menyebabkan kehilangan daya statistik, yang berarti bahwa analisis data mungkin tidak dapat mendeteksi efek nyata yang ada dalam data.
- Hasil yang Tidak Valid: Pelanggaran asumsi dapat menyebabkan hasil analisis yang tidak valid. Ini berarti bahwa hasil analisis tidak dapat digeneralisasikan ke populasi yang lebih luas.
Contoh Kasus Pelanggaran Asumsi Statistik
Misalnya, dalam uji t, asumsi independensi data menyatakan bahwa pengukuran data harus saling independen satu sama lain. Jika asumsi ini dilanggar, misalnya, jika data dikumpulkan dari anggota keluarga yang saling terkait, hasil uji t mungkin tidak valid dan tidak dapat diandalkan. Hal ini karena data yang saling terkait dapat menyebabkan estimasi varians yang salah, yang pada gilirannya dapat memengaruhi nilai p dan kesimpulan uji t.
Teknik Transformasi Data
Transformasi data merupakan teknik yang penting dalam analisis statistik, khususnya dalam mengatasi pelanggaran asumsi normalitas data. Asumsi normalitas merupakan syarat penting dalam banyak uji statistik parametrik. Jika data tidak terdistribusi normal, maka hasil uji statistik parametrik bisa menjadi tidak valid. Transformasi data bertujuan untuk mengubah data asli menjadi data yang terdistribusi lebih normal, sehingga memungkinkan kita untuk menggunakan uji statistik parametrik.
Teknik Transformasi Data
Transformasi data adalah proses mengubah data asli menjadi data yang terdistribusi lebih normal. Beberapa teknik transformasi data yang umum digunakan:
- Logaritma: Transformasi logaritma biasanya digunakan untuk data yang memiliki distribusi skewed ke kanan (positively skewed). Transformasi ini mengurangi pengaruh nilai ekstrem dan membuat distribusi data lebih simetris.
- Akar Kuadrat: Transformasi akar kuadrat juga efektif untuk data yang skewed ke kanan, tetapi lebih lembut daripada transformasi logaritma. Transformasi ini lebih cocok untuk data yang memiliki nilai nol atau negatif.
- Transformasi Box-Cox: Transformasi Box-Cox merupakan transformasi yang lebih umum dan fleksibel. Transformasi ini dapat menentukan transformasi yang paling optimal untuk data tertentu.
Simpulan Akhir
Memilih antara statistik parametrik dan nonparametrik bergantung pada karakteristik data dan tujuan penelitian. Statistik parametrik menawarkan kekuatan dalam pengujian hipotesis, tetapi memerlukan asumsi yang ketat. Statistik nonparametrik lebih fleksibel dan cocok untuk data yang tidak memenuhi asumsi parametrik. Penting untuk memahami kedua pendekatan ini dan memilih metode yang paling tepat untuk mendapatkan hasil analisis yang akurat dan bermakna.




