Contoh soal stack dan jawabannya – Stack, struktur data yang mengikuti prinsip Last-In, First-Out (LIFO), memiliki peran penting dalam ilmu komputer. Bayangkan tumpukan piring di dapur: piring terakhir yang ditumpuk akan menjadi yang pertama diambil. Konsep ini serupa dengan cara stack bekerja, menyimpan dan mengambil data secara berurutan.
Dalam artikel ini, kita akan menjelajahi dunia stack dengan contoh soal dan jawabannya. Anda akan belajar tentang operasi dasar stack, implementasinya, aplikasi dalam kehidupan nyata, dan bahkan tantangan dalam penggunaannya. Siap untuk menyelami struktur data yang menarik ini?
Pengertian Stack
Stack merupakan salah satu struktur data yang sangat penting dalam ilmu komputer. Struktur data ini bekerja dengan prinsip Last In, First Out (LIFO), yang berarti elemen terakhir yang dimasukkan ke dalam stack akan menjadi elemen pertama yang dikeluarkan.
Contoh Analogi Dunia Nyata
Analogi yang mudah dipahami untuk stack adalah tumpukan piring di dapur. Piring terakhir yang ditumpuk akan menjadi piring pertama yang diambil saat kita ingin menggunakannya. Begitu pula dengan stack, elemen yang terakhir dimasukkan akan menjadi elemen pertama yang dikeluarkan.
Perbandingan Stack dengan Struktur Data Lain
Berikut adalah tabel yang membandingkan stack dengan struktur data lain seperti queue dan linked list:
| Fitur | Stack | Queue | Linked List |
|---|---|---|---|
| Prinsip Kerja | LIFO (Last In, First Out) | FIFO (First In, First Out) | Urutan Elemen Fleksibel |
| Akses Elemen | Hanya elemen teratas yang dapat diakses | Hanya elemen terdepan yang dapat diakses | Semua elemen dapat diakses |
| Operasi Umum | Push, Pop, Peek, isEmpty | Enqueue, Dequeue, Peek, isEmpty | Insert, Delete, Search, Traverse |
| Contoh Aplikasi | Fungsi rekursif, Undo/Redo dalam editor teks | Antrian cetak, antrian panggilan telepon | Daftar kontak, daftar item belanja |
Operasi Stack
Stack adalah struktur data linear yang mengikuti prinsip Last-In, First-Out (LIFO). Artinya, elemen terakhir yang ditambahkan ke stack adalah elemen pertama yang dihapus. Bayangkan stack seperti tumpukan piring: piring terakhir yang ditambahkan ke tumpukan adalah piring pertama yang diambil.
Operasi Dasar Stack
Operasi dasar stack memungkinkan kita untuk memanipulasi data yang tersimpan dalam stack. Berikut adalah operasi dasar stack:
- Push: Menambahkan elemen baru ke bagian atas stack.
- Pop: Menghapus elemen teratas dari stack.
- Peek: Mengembalikan nilai elemen teratas dari stack tanpa menghapusnya.
- isEmpty: Mengembalikan nilai boolean (true atau false) yang menunjukkan apakah stack kosong.
Penjelasan Operasi Stack
Mari kita bahas lebih detail tentang setiap operasi stack:
- Push: Operasi push menambahkan elemen baru ke bagian atas stack. Misalnya, jika kita memiliki stack yang berisi elemen [1, 2, 3] dan kita melakukan push dengan elemen 4, stack akan menjadi [1, 2, 3, 4].
- Pop: Operasi pop menghapus elemen teratas dari stack dan mengembalikan nilainya. Misalnya, jika kita memiliki stack yang berisi elemen [1, 2, 3] dan kita melakukan pop, stack akan menjadi [1, 2] dan nilai 3 akan dikembalikan.
- Peek: Operasi peek mengembalikan nilai elemen teratas dari stack tanpa menghapusnya. Misalnya, jika kita memiliki stack yang berisi elemen [1, 2, 3] dan kita melakukan peek, nilai 3 akan dikembalikan dan stack tetap menjadi [1, 2, 3].
- isEmpty: Operasi isEmpty mengembalikan nilai boolean (true atau false) yang menunjukkan apakah stack kosong. Misalnya, jika stack kosong, isEmpty akan mengembalikan true, dan jika stack berisi elemen, isEmpty akan mengembalikan false.
Contoh Kode Pseudocode
Berikut adalah contoh kode pseudocode untuk operasi stack:
// Deklarasi stack
stack = []
// Push elemen ke stack
push(stack, 4)
// Pop elemen dari stack
pop(stack)
// Peek elemen teratas dari stack
peek(stack)
// Cek apakah stack kosong
isEmpty(stack)
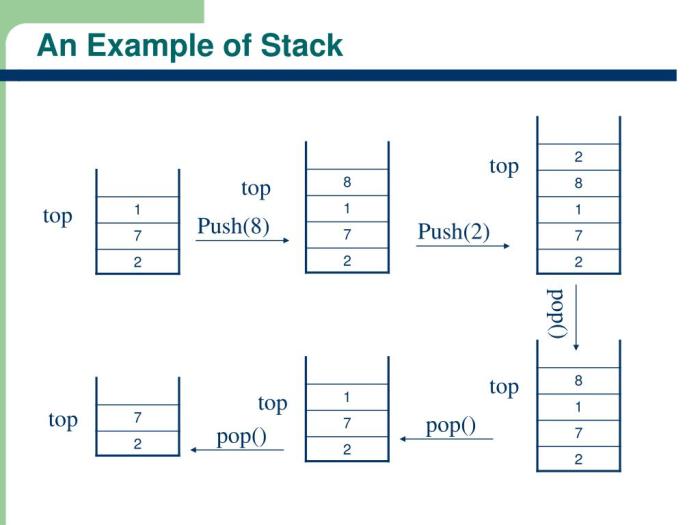
Ilustrasi Operasi Push dan Pop
Berikut adalah ilustrasi yang menunjukkan bagaimana operasi push dan pop bekerja pada stack:
Ilustrasi Push:
* Sebelum Push: [1, 2, 3]
* Elemen yang di-push: 4
* Setelah Push: [1, 2, 3, 4]
Ilustrasi Pop:
* Sebelum Pop: [1, 2, 3, 4]
* Elemen yang di-pop: 4
* Setelah Pop: [1, 2, 3]
Seperti yang terlihat dari ilustrasi, operasi push menambahkan elemen baru ke bagian atas stack, sedangkan operasi pop menghapus elemen teratas dari stack.
Implementasi Stack: Contoh Soal Stack Dan Jawabannya
Stack adalah struktur data yang mengikuti prinsip LIFO (Last In, First Out), yang berarti elemen terakhir yang dimasukkan ke dalam stack akan menjadi elemen pertama yang dikeluarkan. Implementasi stack dapat dilakukan dengan menggunakan berbagai struktur data seperti array, linked list, dan lain sebagainya.
Implementasi Stack dengan Array
Implementasi stack dengan array merupakan salah satu cara yang umum dilakukan. Pada implementasi ini, kita akan menggunakan array untuk menyimpan elemen-elemen stack. Untuk mengelola stack, kita perlu mendefinisikan beberapa operasi dasar, seperti:
- push(data): Menambahkan elemen baru ke bagian atas stack.
- pop(): Mengeluarkan elemen teratas dari stack.
- peek(): Mengembalikan elemen teratas dari stack tanpa mengeluarkannya.
- isEmpty(): Mengembalikan True jika stack kosong, False jika tidak.
- isFull(): Mengembalikan True jika stack penuh, False jika tidak.
Berikut adalah contoh implementasi stack dengan array dalam bahasa Python:
“`python
class Stack:
def __init__(self, capacity):
self.capacity = capacity
self.array = [None] * capacity
self.top = -1def push(self, data):
if self.isFull():
print(“Stack Overflow!”)
return
self.top += 1
self.array[self.top] = datadef pop(self):
if self.isEmpty():
print(“Stack Underflow!”)
return
data = self.array[self.top]
self.top -= 1
return datadef peek(self):
if self.isEmpty():
print(“Stack is empty!”)
return
return self.array[self.top]def isEmpty(self):
return self.top == -1def isFull(self):
return self.top == self.capacity – 1
“`
Contoh penggunaan stack:
“`python
stack = Stack(5)
stack.push(10)
stack.push(20)
stack.push(30)
print(stack.pop()) # Output: 30
print(stack.peek()) # Output: 20
“`
Contoh Penggunaan Stack: Mengecek Tanda Kurung Seimbang
Stack dapat digunakan untuk menyelesaikan masalah sederhana seperti mengecek apakah tanda kurung dalam suatu ekspresi seimbang atau tidak. Misalkan kita memiliki ekspresi “( [ ] )”. Ekspresi ini seimbang karena setiap tanda kurung buka memiliki tanda kurung tutup yang sesuai dan urutannya benar.
Berikut adalah algoritma untuk mengecek tanda kurung seimbang:
- Buat stack kosong.
- Iterasi melalui setiap karakter dalam ekspresi.
- Jika karakter tersebut adalah tanda kurung buka, push ke stack.
- Jika karakter tersebut adalah tanda kurung tutup, periksa apakah stack kosong. Jika kosong, berarti tanda kurung tidak seimbang. Jika tidak kosong, pop elemen teratas dari stack.
- Jika elemen yang di-pop adalah tanda kurung buka yang sesuai dengan tanda kurung tutup saat ini, lanjutkan ke karakter berikutnya. Jika tidak, berarti tanda kurung tidak seimbang.
- Setelah iterasi selesai, periksa apakah stack kosong. Jika kosong, berarti tanda kurung seimbang. Jika tidak kosong, berarti tanda kurung tidak seimbang.
Contoh implementasi algoritma dalam Python:
“`python
def isBalanced(expression):
stack = []
parentheses = ‘)’: ‘(‘, ”: ”, ‘]’: ‘[‘
for char in expression:
if char in parentheses.values():
stack.append(char)
elif char in parentheses.keys():
if stack and stack[-1] == parentheses[char]:
stack.pop()
else:
return False
return len(stack) == 0expression = “( [ ] )”
print(isBalanced(expression)) # Output: Trueexpression = “( [ ] )”
print(isBalanced(expression)) # Output: Trueexpression = “( [ ] )”
print(isBalanced(expression)) # Output: True
“`
Aplikasi Stack
Stack, selain konsepnya yang menarik, juga punya banyak aplikasi di dunia nyata. Aplikasi stack membantu dalam berbagai bidang, mulai dari pemrograman hingga desain editor teks. Yuk, kita telusuri beberapa aplikasi stack yang sering kita jumpai!
Manajemen Fungsi dalam Program
Stack memegang peranan penting dalam manajemen fungsi dalam program. Bayangkan ketika kamu menjalankan program, program tersebut akan memanggil fungsi-fungsi tertentu untuk menyelesaikan tugasnya. Stack membantu melacak fungsi mana yang sedang dijalankan dan bagaimana mereka saling berhubungan.
- Ketika suatu fungsi dipanggil, alamat memori dari fungsi tersebut akan disimpan di stack.
- Ketika fungsi tersebut selesai, alamat memori tersebut dihapus dari stack, dan program akan kembali ke fungsi sebelumnya.
Proses ini memastikan bahwa program dapat kembali ke fungsi sebelumnya dengan benar, dan menghindari kesalahan yang bisa terjadi jika fungsi tidak dikelola dengan baik.
Undo/Redo dalam Editor Teks
Kamu pasti pernah menggunakan fitur Undo/Redo dalam editor teks. Fitur ini memungkinkanmu untuk membatalkan atau mengulang perubahan yang kamu buat pada dokumen. Stack berperan penting dalam fitur Undo/Redo ini.
- Setiap kali kamu membuat perubahan pada dokumen, perubahan tersebut disimpan dalam stack.
- Ketika kamu menekan tombol Undo, editor teks akan mengambil perubahan terakhir dari stack dan membatalkannya.
- Ketika kamu menekan tombol Redo, editor teks akan mengambil perubahan yang telah dibatalkan dari stack dan menerapkannya kembali.
Stack membantu editor teks untuk menyimpan dan melacak perubahan yang dilakukan, sehingga fitur Undo/Redo dapat berfungsi dengan baik.
Penanganan Ekspresi Aritmatika
Stack juga berperan dalam penanganan ekspresi aritmatika. Ekspresi aritmatika, seperti “2 + 3 * 4”, melibatkan operasi matematika yang dilakukan dalam urutan tertentu. Stack membantu dalam mengevaluasi ekspresi tersebut dengan cara:
- Operan (angka) dalam ekspresi akan disimpan dalam stack.
- Operator (tanda tambah, kurang, kali, bagi) akan diproses sesuai urutan prioritasnya.
- Hasil dari setiap operasi akan disimpan kembali dalam stack.
Dengan cara ini, stack membantu komputer untuk mengevaluasi ekspresi aritmatika dengan benar.
Tabel Aplikasi Stack
| Aplikasi | Contoh Penggunaan |
|---|---|
| Manajemen Fungsi | Memanggil fungsi dalam program, seperti fungsi untuk menghitung luas persegi panjang atau menampilkan pesan di layar. |
| Undo/Redo | Membatalkan atau mengulang perubahan yang dilakukan pada dokumen di editor teks. |
| Penanganan Ekspresi Aritmatika | Mengevaluasi ekspresi matematika seperti “2 + 3 * 4” dengan benar. |
| Backtracking | Mencari solusi pada algoritma pencarian seperti Sudoku atau permainan catur. |
| Kompilator | Memproses kode program dan mengubahnya menjadi kode mesin. |
Soal Latihan Stack
Stack merupakan struktur data yang menggunakan prinsip LIFO (Last In First Out), di mana elemen terakhir yang dimasukkan ke dalam stack akan menjadi elemen pertama yang dikeluarkan. Untuk menguji pemahamanmu tentang stack, berikut adalah 5 soal latihan yang meliputi operasi dan aplikasi stack.
Soal Latihan Stack
Soal latihan berikut akan menguji pemahamanmu tentang operasi dasar stack dan bagaimana stack dapat diterapkan dalam berbagai kasus.
- Soal 1: Operasi Push dan Pop
Perhatikan stack yang awalnya kosong. Lakukan operasi push dengan nilai 1, 2, 3, dan 4 secara berurutan. Kemudian, lakukan operasi pop sebanyak 2 kali. Tuliskan nilai yang dikeluarkan dari stack dan keadaan stack setelah operasi pop.
Jawaban:
Contoh soal stack dan jawabannya bisa membantu kamu memahami konsep dasar data struktur ini. Misalnya, soal tentang cara menambahkan dan menghapus data dalam stack. Nah, kalau kamu lagi mau masuk kerja di RS Muhammadiyah, kamu juga bisa belajar dari contoh soal dan jawaban tes masuk RS Muhammadiyah yang ada di internet.
Dengan mempelajari contoh soal dan jawaban, kamu bisa mempersiapkan diri lebih matang dan meningkatkan peluang lolos seleksi.
Setelah operasi push, stack akan berisi: 4, 3, 2, 1 (dari atas ke bawah). Setelah dua kali pop, nilai yang dikeluarkan adalah 4 dan 3. Stack akan berisi: 2, 1.
- Soal 2: Implementasi Stack dengan Array
Tuliskan algoritma untuk mengimplementasikan stack menggunakan array. Algoritma harus mencakup operasi push, pop, peek, dan isEmpty.
Jawaban:
Berikut adalah algoritma untuk mengimplementasikan stack menggunakan array:
- Push: Tambahkan elemen baru ke indeks terakhir array. Jika array sudah penuh, tangani overflow.
- Pop: Hapus dan kembalikan elemen dari indeks terakhir array. Jika array kosong, tangani underflow.
- Peek: Kembalikan elemen dari indeks terakhir array tanpa menghapusnya.
- IsEmpty: Periksa apakah array kosong.
- Soal 3: Aplikasi Stack dalam Reverse String
Jelaskan bagaimana stack dapat digunakan untuk membalikkan sebuah string.
Jawaban:
Stack dapat digunakan untuk membalikkan string dengan cara berikut:
- Iterasi melalui setiap karakter dalam string.
- Dorong setiap karakter ke dalam stack.
- Pop setiap karakter dari stack dan tambahkan ke string baru.
String baru akan menjadi string asli yang dibalik.
- Soal 4: Aplikasi Stack dalam Pencocokan Kurung
Jelaskan bagaimana stack dapat digunakan untuk menentukan apakah kurung dalam ekspresi matematika seimbang.
Jawaban:
Stack dapat digunakan untuk menentukan keseimbangan kurung dengan cara berikut:
- Iterasi melalui setiap karakter dalam ekspresi.
- Jika karakter adalah kurung buka (seperti ‘(‘), dorong ke stack.
- Jika karakter adalah kurung tutup (seperti ‘)’), periksa apakah stack kosong. Jika tidak kosong, pop elemen teratas dari stack. Jika stack kosong atau elemen teratas bukan kurung buka yang sesuai, ekspresi tidak seimbang.
Setelah iterasi selesai, jika stack kosong, ekspresi seimbang. Jika tidak, ekspresi tidak seimbang.
- Soal 5: Aplikasi Stack dalam Undo/Redo
Jelaskan bagaimana stack dapat digunakan untuk mengimplementasikan fungsi undo/redo dalam aplikasi editor teks.
Jawaban:
Stack dapat digunakan untuk mengimplementasikan undo/redo dengan cara berikut:
- Setiap perubahan pada teks didorong ke stack sebagai objek yang mewakili perubahan tersebut (misalnya, menambahkan karakter, menghapus karakter, memindahkan teks).
- Operasi undo dilakukan dengan me-pop perubahan terakhir dari stack dan membatalkannya.
- Operasi redo dilakukan dengan me-push kembali perubahan yang dibatalkan ke stack dan menerapkannya kembali.
Variasi Stack
Stack merupakan struktur data yang bekerja berdasarkan prinsip Last-In, First-Out (LIFO). Artinya, elemen terakhir yang dimasukkan ke dalam stack akan menjadi elemen pertama yang dikeluarkan. Namun, selain stack LIFO, terdapat juga jenis stack lainnya yang disebut stack FIFO.
Stack LIFO (Last-In, First-Out)
Stack LIFO adalah jenis stack yang paling umum. Dalam stack LIFO, elemen terakhir yang ditambahkan ke dalam stack akan menjadi elemen pertama yang dihapus. Contoh penggunaan stack LIFO dalam program:
- Manajemen panggilan fungsi: Saat suatu fungsi dipanggil, alamat pengembalian dan parameter fungsi disimpan dalam stack. Ketika fungsi selesai, alamat pengembalian diambil dari stack dan program kembali ke titik panggilan awal.
- Undo/Redo: Banyak aplikasi menggunakan stack untuk menyimpan operasi yang dilakukan pengguna. Saat pengguna menekan tombol “Undo”, operasi terakhir yang disimpan di stack dihapus dan dibalik.
Stack FIFO (First-In, First-Out)
Stack FIFO, yang juga dikenal sebagai queue, bekerja dengan prinsip First-In, First-Out. Elemen pertama yang ditambahkan ke dalam stack akan menjadi elemen pertama yang dihapus. Contoh penggunaan stack FIFO dalam program:
- Antrean cetak: Saat beberapa dokumen diantrikan untuk dicetak, dokumen pertama yang masuk ke dalam antrean akan menjadi dokumen pertama yang dicetak.
- Manajemen proses: Sistem operasi menggunakan queue untuk mengelola proses yang sedang berjalan. Proses pertama yang masuk ke dalam queue akan menjadi proses pertama yang dijalankan.
Penerapan Stack dalam Algoritma
Stack adalah struktur data yang mengikuti prinsip LIFO (Last In, First Out), di mana elemen terakhir yang dimasukkan ke dalam stack akan menjadi elemen pertama yang dikeluarkan. Prinsip ini memungkinkan stack untuk digunakan dalam berbagai algoritma, terutama dalam situasi di mana urutan operasi atau data penting.
Algoritma Pencarian Kedalaman (DFS)
Algoritma Pencarian Kedalaman (Depth-First Search) merupakan salah satu algoritma pencarian yang umum digunakan untuk menjelajahi graf. DFS menggunakan stack untuk menyimpan simpul yang belum dikunjungi. Berikut adalah langkah-langkah DFS:
- Tandai simpul awal sebagai simpul yang sudah dikunjungi.
- Dorong simpul awal ke dalam stack.
- Selama stack tidak kosong:
- Pop simpul teratas dari stack.
- Untuk setiap simpul yang berdekatan dengan simpul yang di-pop, jika simpul tersebut belum dikunjungi:
- Tandai simpul yang berdekatan sebagai simpul yang sudah dikunjungi.
- Dorong simpul yang berdekatan ke dalam stack.
Contoh kode DFS dengan stack dalam Python:
def dfs(graph, start):
visited = set()
stack = [start]while stack:
node = stack.pop()
if node not in visited:
visited.add(node)
print(node)
for neighbor in graph[node]:
if neighbor not in visited:
stack.append(neighbor)graph =
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': [],
'F': []dfs(graph, 'A')
Dalam kode di atas, stack digunakan untuk menyimpan simpul yang belum dikunjungi. Ketika sebuah simpul di-pop dari stack, simpul tersebut diproses dan tetangganya yang belum dikunjungi didorong ke dalam stack.
Algoritma Konversi Ekspresi Infix ke Postfix, Contoh soal stack dan jawabannya
Ekspresi infix adalah ekspresi matematika yang menggunakan operator di antara operand. Ekspresi postfix, di sisi lain, menggunakan operator setelah operand. Algoritma konversi ekspresi infix ke postfix menggunakan stack untuk membantu proses konversi.
Berikut adalah langkah-langkah konversi ekspresi infix ke postfix:
- Buat stack kosong untuk menyimpan operator.
- Siapkan string kosong untuk menyimpan ekspresi postfix.
- Untuk setiap token dalam ekspresi infix:
- Jika token adalah operand, tambahkan token tersebut ke ekspresi postfix.
- Jika token adalah operator:
- Jika stack kosong atau token adalah kurung buka, dorong token tersebut ke dalam stack.
- Jika token adalah kurung tutup, pop semua operator dari stack dan tambahkan ke ekspresi postfix hingga kurung buka di-pop dari stack.
- Jika token adalah operator dan prioritasnya lebih tinggi dari operator teratas di stack, dorong token tersebut ke dalam stack.
- Jika token adalah operator dan prioritasnya lebih rendah atau sama dengan operator teratas di stack, pop operator dari stack dan tambahkan ke ekspresi postfix hingga operator teratas di stack memiliki prioritas lebih rendah atau stack kosong.
- Setelah semua token diproses, pop semua operator yang tersisa dari stack dan tambahkan ke ekspresi postfix.
Contoh kode konversi ekspresi infix ke postfix dengan stack dalam Python:
def infix_to_postfix(infix):
stack = []
postfix = ''
precedence = '+': 1, '-': 1, '*': 2, '/': 2, '^': 3for token in infix:
if token.isalnum():
postfix += token
elif token == '(':
stack.append(token)
elif token == ')':
while stack and stack[-1] != '(':
postfix += stack.pop()
stack.pop()
else:
while stack and precedence[token] <= precedence[stack[-1]]:
postfix += stack.pop()
stack.append(token)while stack:
postfix += stack.pop()return postfix
infix = 'A + B * C - D / E'
postfix = infix_to_postfix(infix)
print(postfix)
Dalam kode di atas, stack digunakan untuk menyimpan operator. Ketika sebuah operator di-pop dari stack, operator tersebut ditambahkan ke ekspresi postfix. Prioritas operator digunakan untuk menentukan urutan operasi.
Kesulitan dalam Implementasi Stack
Stack merupakan struktur data yang penting dalam ilmu komputer. Implementasinya bisa dibilang mudah, tetapi ada beberapa kesulitan yang perlu diatasi untuk mencapai implementasi stack yang optimal dan efisien. Berikut adalah beberapa kesulitan umum yang dihadapi saat mengimplementasikan stack.
Memilih Struktur Data yang Tepat
Memilih struktur data yang tepat untuk implementasi stack sangat penting. Pilihan struktur data akan memengaruhi kinerja dan fleksibilitas stack. Ada beberapa pilihan struktur data yang umum digunakan, seperti array, linked list, dan tree.
- Array: Struktur data ini cocok untuk implementasi stack yang sederhana dan efisien, terutama jika ukuran stack sudah diketahui sebelumnya. Namun, array memiliki keterbatasan dalam hal fleksibilitas karena ukurannya tetap.
- Linked list: Struktur data ini menawarkan fleksibilitas yang lebih besar dibandingkan array, karena ukurannya dapat berubah secara dinamis. Namun, implementasi linked list bisa lebih kompleks dan mungkin kurang efisien dibandingkan array untuk operasi tertentu.
- Tree: Struktur data ini bisa digunakan untuk implementasi stack yang lebih kompleks, seperti stack yang mendukung operasi pencarian yang cepat. Namun, implementasi tree bisa lebih rumit dan membutuhkan lebih banyak memori.
Pilihan struktur data yang tepat tergantung pada kebutuhan dan kendala implementasi stack. Pertimbangan seperti ukuran stack, operasi yang sering dilakukan, dan kebutuhan memori perlu dipertimbangkan.
Mengatasi Overflow dan Underflow Stack
Overflow dan underflow merupakan masalah umum yang dihadapi saat mengimplementasikan stack. Overflow terjadi ketika stack penuh dan tidak ada ruang lagi untuk menambahkan elemen baru. Underflow terjadi ketika stack kosong dan tidak ada elemen yang bisa diambil.
- Overflow: Solusi untuk mengatasi overflow adalah dengan memperluas kapasitas stack, misalnya dengan menggunakan teknik realokasi memori.
- Underflow: Solusi untuk mengatasi underflow adalah dengan memeriksa kondisi stack sebelum melakukan operasi pengambilan elemen. Jika stack kosong, maka operasi pengambilan harus dihentikan dan pesan kesalahan harus ditampilkan.
Penting untuk mempertimbangkan dan mengimplementasikan mekanisme penanganan overflow dan underflow yang tepat untuk memastikan stabilitas dan keandalan stack.
Pengembangan Lebih Lanjut
Meskipun konsep stack sederhana, pengembangan lebih lanjut memungkinkan penerapannya yang lebih kompleks dan fleksibel dalam berbagai skenario. Ini meliputi modifikasi struktural, penambahan fungsi, dan penerapan stack dalam sistem operasi.
Stack dengan Batasan Ukuran
Dalam implementasi stack standar, ukuran stack tidak dibatasi. Namun, dalam situasi nyata, memori yang tersedia terbatas. Oleh karena itu, stack dengan batasan ukuran penting untuk mencegah overflow stack, yaitu kondisi ketika stack mencoba menyimpan data melebihi kapasitasnya, yang dapat menyebabkan crash program.
- Salah satu teknik yang umum digunakan adalah menggunakan stack dengan ukuran tetap yang ditentukan saat inisialisasi. Jika stack penuh, operasi push akan ditolak.
- Teknik lainnya adalah menggunakan stack yang dinamis, yang dapat memperluas ukurannya secara otomatis saat dibutuhkan. Namun, perlu diingat bahwa perluasan ini dapat menyebabkan overhead kinerja dan kompleksitas manajemen memori.
Stack dengan Fungsi Khusus
Stack dasar hanya menyediakan operasi push dan pop. Namun, stack dapat diperkaya dengan fungsi khusus untuk memenuhi kebutuhan tertentu.
- Contohnya, stack dapat dilengkapi dengan fungsi peek untuk melihat elemen teratas tanpa menghapusnya, atau fungsi search untuk mencari elemen tertentu dalam stack.
- Fungsi-fungsi khusus ini dapat meningkatkan efisiensi dan fleksibilitas stack dalam aplikasi tertentu, seperti pengolahan data, pemrosesan bahasa, dan sistem operasi.
Penggunaan Stack dalam Sistem Operasi
Stack memegang peran penting dalam sistem operasi, khususnya dalam manajemen proses dan pemanggilan fungsi.
- Saat suatu proses dibuat, sistem operasi mengalokasikan ruang stack untuk menyimpan informasi terkait proses tersebut, seperti variabel lokal, parameter fungsi, dan alamat pengembalian.
- Stack juga digunakan untuk menyimpan informasi tentang fungsi yang sedang dieksekusi, seperti parameter dan alamat pengembalian, yang memungkinkan sistem operasi untuk mengembalikan eksekusi ke fungsi yang benar setelah fungsi yang sedang dieksekusi selesai.
- Penggunaan stack dalam sistem operasi memungkinkan proses-proses untuk berbagi sumber daya dengan aman dan efisien.
Potensi Pengembangan dan Penelitian di Bidang Stack
Meskipun stack telah lama digunakan dalam berbagai bidang, penelitian dan pengembangan di bidang stack masih terus berlanjut.
- Salah satu area fokus adalah pengembangan algoritma dan struktur data yang lebih efisien dan scalable untuk mengelola stack dalam skenario yang kompleks, seperti dalam pemrosesan data skala besar atau komputasi paralel.
- Penelitian juga dilakukan untuk meningkatkan keamanan stack, khususnya untuk mencegah eksploitasi kerentanan stack overflow yang dapat digunakan oleh penyerang untuk mengambil alih kontrol program.
Akhir Kata
Memahami stack adalah langkah penting dalam perjalanan belajar ilmu komputer. Dari mengelola fungsi program hingga menangani ekspresi aritmatika, stack hadir dalam berbagai aplikasi. Dengan latihan soal dan pemahaman yang mendalam, Anda akan siap menghadapi berbagai tantangan dalam pengembangan perangkat lunak dan algoritma.




