Uji t, sebuah alat statistik yang kuat, membantu kita dalam menguji hipotesis tentang perbedaan rata-rata. Mempelajari contoh soal uji t dan penyelesaiannya akan membantu Anda memahami bagaimana uji t diterapkan dalam penelitian dan bagaimana menginterpretasikan hasilnya.
Artikel ini akan membahas berbagai jenis uji t, mulai dari uji t satu sampel hingga uji t dua sampel berpasangan. Kita akan mempelajari langkah-langkah melakukan uji t, asumsi yang perlu dipenuhi, dan bagaimana menginterpretasikan hasilnya. Selain itu, kita akan membahas beberapa contoh soal uji t dengan penyelesaiannya secara detail.
Pengertian Uji t
Uji t merupakan salah satu metode statistik yang digunakan untuk membandingkan rata-rata dua kelompok data. Metode ini sangat berguna dalam penelitian ilmiah, khususnya dalam bidang kesehatan, ekonomi, dan sosial. Uji t memungkinkan kita untuk menguji hipotesis tentang perbedaan rata-rata populasi berdasarkan sampel data yang dikumpulkan.
Jenis-Jenis Uji t
Terdapat beberapa jenis uji t yang umum digunakan, dibedakan berdasarkan tujuan dan desain penelitian. Berikut adalah jenis-jenis uji t yang umum digunakan:
- Uji t satu sampel: Uji ini digunakan untuk membandingkan rata-rata sampel dengan nilai rata-rata populasi yang telah diketahui. Contohnya, Anda ingin mengetahui apakah rata-rata tinggi badan mahasiswa di suatu universitas berbeda secara signifikan dari rata-rata tinggi badan pria dewasa di Indonesia.
- Uji t dua sampel: Uji ini digunakan untuk membandingkan rata-rata dua kelompok sampel yang independen. Contohnya, Anda ingin mengetahui apakah terdapat perbedaan signifikan antara rata-rata nilai ujian mahasiswa yang mengikuti metode pembelajaran online dan mahasiswa yang mengikuti metode pembelajaran konvensional.
- Uji t berpasangan: Uji ini digunakan untuk membandingkan rata-rata dua kelompok sampel yang berpasangan, biasanya data yang dikumpulkan dari subjek yang sama pada dua waktu yang berbeda. Contohnya, Anda ingin mengetahui apakah terdapat perbedaan signifikan antara skor tekanan darah pasien sebelum dan sesudah mengonsumsi obat tertentu.
Contoh Skenario Penelitian
Bayangkan Anda ingin mengetahui apakah terdapat perbedaan signifikan antara tingkat kepuasan pelanggan terhadap dua jenis produk yang berbeda. Anda melakukan survei kepuasan pelanggan terhadap kedua produk tersebut dan mendapatkan data berupa skor kepuasan pelanggan. Untuk menguji hipotesis Anda, Anda dapat menggunakan uji t dua sampel.
Asumsi Uji t
Uji t adalah salah satu metode statistik yang umum digunakan untuk membandingkan rata-rata dua kelompok data. Namun, uji t memiliki asumsi yang harus dipenuhi sebelum dapat diterapkan. Penting untuk memahami dan memverifikasi asumsi ini untuk memastikan validitas hasil uji t.
Asumsi Uji t
Sebelum melakukan uji t, ada beberapa asumsi yang harus dipenuhi. Asumsi ini penting untuk memastikan bahwa hasil uji t akurat dan dapat diandalkan. Berikut adalah beberapa asumsi uji t:
- Data harus berdistribusi normal.
- Varians kedua kelompok data harus sama.
- Data harus independen.
Pentingnya Asumsi Uji t
Asumsi uji t penting untuk memastikan bahwa hasil uji t valid. Jika asumsi ini tidak dipenuhi, hasil uji t mungkin tidak akurat dan dapat menyebabkan kesimpulan yang salah.
- Jika data tidak berdistribusi normal, uji t mungkin tidak akurat, terutama untuk sampel kecil.
- Jika varians kedua kelompok data tidak sama, uji t mungkin tidak akurat, dan dapat menyebabkan kesimpulan yang salah tentang perbedaan rata-rata.
- Jika data tidak independen, uji t mungkin tidak akurat, karena dapat menyebabkan kesalahan dalam menghitung derajat kebebasan.
Cara Memeriksa Asumsi Uji t
Ada beberapa cara untuk memeriksa asumsi uji t. Salah satu cara adalah dengan menggunakan software statistika seperti SPSS atau R. Software ini menyediakan berbagai macam uji statistik yang dapat digunakan untuk memeriksa asumsi uji t.
- Untuk memeriksa asumsi normalitas, kita dapat menggunakan uji Shapiro-Wilk atau uji Kolmogorov-Smirnov. Uji ini akan menghasilkan nilai p yang menunjukkan apakah data berdistribusi normal atau tidak.
- Untuk memeriksa asumsi kesamaan varians, kita dapat menggunakan uji Levene atau uji F. Uji ini akan menghasilkan nilai p yang menunjukkan apakah varians kedua kelompok data sama atau tidak.
- Untuk memeriksa asumsi independensi, kita perlu melihat desain penelitian dan memastikan bahwa data dikumpulkan secara independen.
Contoh Cara Memeriksa Asumsi Uji t dengan Menggunakan Software Statistika
Sebagai contoh, mari kita asumsikan bahwa kita ingin membandingkan rata-rata tinggi badan antara pria dan wanita. Kita dapat menggunakan SPSS untuk memeriksa asumsi uji t.
- Pertama, kita perlu memasukkan data tinggi badan pria dan wanita ke dalam SPSS.
- Kemudian, kita dapat menggunakan menu “Analyze” > “Descriptive Statistics” > “Explore” untuk memeriksa asumsi normalitas dan kesamaan varians.
- Dalam jendela “Explore”, kita perlu memilih variabel tinggi badan dan kelompok gender.
- Kemudian, kita dapat memilih “Plots” > “Normality plots with tests” untuk memeriksa asumsi normalitas.
- Kita juga dapat memilih “Plots” > “Boxplots” untuk memeriksa asumsi kesamaan varians.
Kesimpulan
Memeriksa asumsi uji t adalah langkah penting sebelum melakukan uji t. Jika asumsi ini tidak dipenuhi, hasil uji t mungkin tidak akurat. Software statistika seperti SPSS atau R dapat membantu kita dalam memeriksa asumsi uji t.
Langkah-Langkah Melakukan Uji t
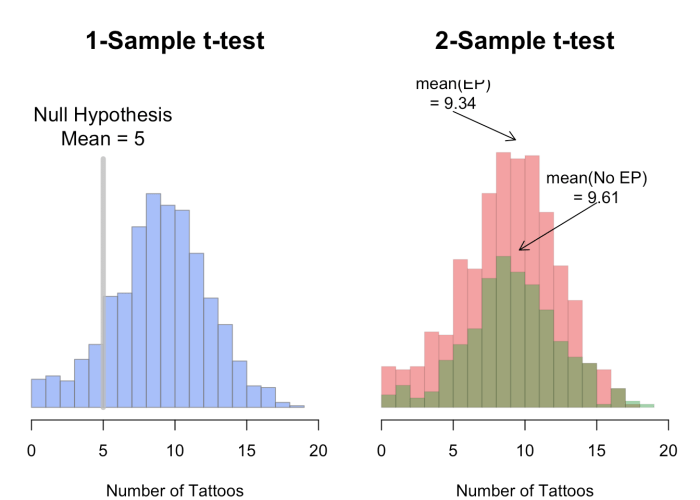
Uji t merupakan salah satu alat statistik yang kuat untuk membandingkan rata-rata dari dua kelompok data. Uji ini membantu kita untuk menentukan apakah terdapat perbedaan signifikan antara kedua kelompok tersebut, atau apakah perbedaan tersebut hanya terjadi secara kebetulan. Langkah-langkah melakukan uji t dapat diuraikan sebagai berikut:
Langkah 1: Merumuskan Hipotesis
Langkah pertama dalam melakukan uji t adalah merumuskan hipotesis nol dan hipotesis alternatif. Hipotesis nol menyatakan bahwa tidak ada perbedaan signifikan antara rata-rata kedua kelompok. Sementara hipotesis alternatif menyatakan bahwa terdapat perbedaan signifikan antara rata-rata kedua kelompok. Misalnya, kita ingin mengetahui apakah terdapat perbedaan signifikan antara tinggi badan siswa laki-laki dan perempuan di suatu sekolah. Hipotesis nol akan menyatakan bahwa tidak ada perbedaan signifikan antara tinggi badan siswa laki-laki dan perempuan, sedangkan hipotesis alternatif menyatakan bahwa terdapat perbedaan signifikan antara tinggi badan siswa laki-laki dan perempuan.
Langkah 2: Menentukan Tingkat Signifikansi
Tingkat signifikansi adalah probabilitas menolak hipotesis nol ketika hipotesis nol sebenarnya benar. Tingkat signifikansi biasanya ditetapkan sebesar 0,05, yang berarti bahwa ada peluang 5% untuk menolak hipotesis nol ketika hipotesis nol sebenarnya benar. Artinya, kita hanya akan menolak hipotesis nol jika terdapat bukti kuat yang mendukung hipotesis alternatif.
Langkah 3: Memilih Uji t yang Tepat
Terdapat beberapa jenis uji t yang dapat dipilih, tergantung pada jenis data yang kita miliki dan desain penelitian. Beberapa jenis uji t yang umum digunakan antara lain:
- Uji t satu sampel: Digunakan untuk membandingkan rata-rata sampel dengan rata-rata populasi yang diketahui.
- Uji t dua sampel independen: Digunakan untuk membandingkan rata-rata dua kelompok sampel independen.
- Uji t dua sampel berpasangan: Digunakan untuk membandingkan rata-rata dua kelompok sampel berpasangan.
Langkah 4: Menghitung Statistik Uji t
Statistik uji t dihitung dengan membagi selisih antara rata-rata kedua kelompok dengan kesalahan standar selisih tersebut. Rumus untuk menghitung statistik uji t adalah:
t = (x̄1 – x̄2) / sp√(1/n1 + 1/n2)
di mana:
- x̄1 adalah rata-rata sampel pertama.
- x̄2 adalah rata-rata sampel kedua.
- sp adalah deviasi standar gabungan.
- n1 adalah ukuran sampel pertama.
- n2 adalah ukuran sampel kedua.
Langkah 5: Menghitung Nilai p
Nilai p adalah probabilitas mendapatkan hasil statistik uji t yang sama atau lebih ekstrem jika hipotesis nol benar. Nilai p dihitung dengan menggunakan tabel distribusi t atau dengan menggunakan perangkat lunak statistik. Jika nilai p lebih kecil dari tingkat signifikansi, maka kita menolak hipotesis nol.
Langkah 6: Menginterpretasikan Hasil Uji t
Jika nilai p lebih kecil dari tingkat signifikansi, maka kita menolak hipotesis nol dan menyimpulkan bahwa terdapat perbedaan signifikan antara rata-rata kedua kelompok. Sebaliknya, jika nilai p lebih besar dari tingkat signifikansi, maka kita gagal menolak hipotesis nol dan menyimpulkan bahwa tidak ada perbedaan signifikan antara rata-rata kedua kelompok.
Contoh Tabel Hasil Uji t
| Variabel | Rata-rata | Deviasi Standar | Ukuran Sampel |
|---|---|---|---|
| Tinggi Badan Siswa Laki-laki | 170 cm | 5 cm | 30 |
| Tinggi Badan Siswa Perempuan | 165 cm | 4 cm | 35 |
Hasil uji t menunjukkan bahwa statistik uji t adalah 2,5 dan nilai p adalah 0,01. Karena nilai p lebih kecil dari tingkat signifikansi 0,05, maka kita menolak hipotesis nol dan menyimpulkan bahwa terdapat perbedaan signifikan antara tinggi badan siswa laki-laki dan perempuan di sekolah tersebut.
Contoh soal uji t dan penyelesaiannya memang seringkali jadi bahan diskusi di kelas, ya. Nah, buat kamu yang masih bingung sama sistem persamaan linear dua variabel, coba deh cek contoh soal sistem persamaan linear dua variabel kelas 10 di link ini.
Setelah memahami materi ini, kamu bisa lebih mudah memahami konsep uji t dan penyelesaiannya, lho! Soalnya, uji t sendiri seringkali digunakan untuk menganalisis data yang berkaitan dengan variabel-variabel yang memiliki hubungan linear.
Contoh Soal Uji t Satu Sampel: Contoh Soal Uji T Dan Penyelesaiannya
Uji t satu sampel adalah salah satu jenis uji statistik yang digunakan untuk membandingkan rata-rata sampel dengan rata-rata populasi yang diketahui. Uji ini digunakan untuk menguji hipotesis tentang nilai rata-rata populasi berdasarkan data sampel yang tersedia.
Contoh Soal Uji t Satu Sampel, Contoh soal uji t dan penyelesaiannya
Misalnya, kita ingin mengetahui apakah rata-rata tinggi badan siswa di sebuah sekolah tinggi berbeda secara signifikan dari rata-rata tinggi badan pria dewasa di Indonesia yang diketahui sebesar 168 cm. Untuk itu, kita dapat mengambil sampel 30 siswa dari sekolah tinggi tersebut dan mengukur tinggi badan mereka. Data yang diperoleh dapat kita gunakan untuk melakukan uji t satu sampel.
Langkah-Langkah Penyelesaian Soal Uji t Satu Sampel
Berikut langkah-langkah untuk menyelesaikan soal uji t satu sampel:
- Tentukan hipotesis nol (H0) dan hipotesis alternatif (H1).
- Tentukan tingkat signifikansi (α).
- Hitung statistik uji t.
- Tentukan nilai kritis atau p-value.
- Buat keputusan berdasarkan hasil uji.
Contoh Soal Uji t Satu Sampel, Contoh soal uji t dan penyelesaiannya
Misalkan kita ingin mengetahui apakah rata-rata tinggi badan siswa di sebuah sekolah tinggi berbeda secara signifikan dari rata-rata tinggi badan pria dewasa di Indonesia yang diketahui sebesar 168 cm. Kita mengambil sampel 30 siswa dari sekolah tinggi tersebut dan mengukur tinggi badan mereka. Data yang diperoleh disajikan dalam tabel berikut:
| No. | Tinggi Badan (cm) |
|---|---|
| 1 | 170 |
| 2 | 172 |
| 3 | 168 |
| … | … |
| 30 | 175 |
Langkah-Langkah Penyelesaian Soal Uji t Satu Sampel
Berikut langkah-langkah untuk menyelesaikan soal uji t satu sampel:
- Tentukan hipotesis nol (H0) dan hipotesis alternatif (H1).
H0: μ = 168 cm (Rata-rata tinggi badan siswa sama dengan rata-rata tinggi badan pria dewasa di Indonesia)
H1: μ ≠ 168 cm (Rata-rata tinggi badan siswa berbeda dengan rata-rata tinggi badan pria dewasa di Indonesia) - Tentukan tingkat signifikansi (α).
Misalnya, kita menggunakan tingkat signifikansi α = 0,05. - Hitung statistik uji t.
Rumus statistik uji t satu sampel adalah:
t = (x̄ – μ) / (s / √n)
Dimana:
x̄ = rata-rata sampel
μ = rata-rata populasi
s = standar deviasi sampel
n = ukuran sampel
Berdasarkan data yang diperoleh, kita dapat menghitung rata-rata sampel (x̄) = 171 cm dan standar deviasi sampel (s) = 3 cm.
Sehingga, statistik uji t dapat dihitung sebagai berikut:
t = (171 – 168) / (3 / √30) = 3 / (3 / √30) = 3√30 / 3 = √30 ≈ 5.48
- Tentukan nilai kritis atau p-value.
Nilai kritis untuk uji t satu sampel dengan derajat bebas (df) = n – 1 = 30 – 1 = 29 dan α = 0,05 adalah ±2,045.
Atau, kita dapat menggunakan tabel distribusi t untuk menentukan p-value.
P-value untuk t = 5.48 dan df = 29 adalah kurang dari 0,001. - Buat keputusan berdasarkan hasil uji.
Karena nilai t hitung (5.48) lebih besar dari nilai kritis (2.045) atau p-value (kurang dari 0.001) kurang dari α (0.05), maka kita menolak hipotesis nol (H0).
Ini berarti bahwa ada bukti yang cukup kuat untuk menyimpulkan bahwa rata-rata tinggi badan siswa di sekolah tinggi tersebut berbeda secara signifikan dari rata-rata tinggi badan pria dewasa di Indonesia.
Tabel Data, Hasil Perhitungan, dan Kesimpulan Uji t
Berikut tabel yang menunjukkan data, hasil perhitungan, dan kesimpulan uji t:
| Parameter | Nilai |
|---|---|
| Rata-rata Sampel (x̄) | 171 cm |
| Rata-rata Populasi (μ) | 168 cm |
| Standar Deviasi Sampel (s) | 3 cm |
| Ukuran Sampel (n) | 30 |
| Derajat Bebas (df) | 29 |
| Tingkat Signifikansi (α) | 0.05 |
| Statistik Uji t | 5.48 |
| Nilai Kritis | ±2.045 |
| P-value | Kurang dari 0.001 |
| Keputusan | Tolak H0 |
| Kesimpulan | Ada bukti yang cukup kuat untuk menyimpulkan bahwa rata-rata tinggi badan siswa di sekolah tinggi tersebut berbeda secara signifikan dari rata-rata tinggi badan pria dewasa di Indonesia. |
Contoh Soal Uji t Dua Sampel Bebas
Uji t dua sampel bebas digunakan untuk membandingkan rata-rata dua kelompok independen. Contohnya, kita ingin membandingkan rata-rata tinggi badan siswa laki-laki dan perempuan di suatu sekolah. Dalam uji t dua sampel bebas, kita mengasumsikan bahwa data berdistribusi normal dan varians kedua kelompok sama.
Contoh Soal
Sebuah perusahaan farmasi ingin menguji efektivitas dua jenis obat penurun tekanan darah. Dua kelompok sampel yang terdiri dari 20 orang masing-masing diberi obat A dan obat B. Data tekanan darah sebelum dan sesudah pemberian obat dicatat dan hasilnya disajikan dalam tabel berikut:
| Obat | Tekanan Darah Sebelum | Tekanan Darah Sesudah |
|---|---|---|
| A | 140 | 130 |
| A | 150 | 140 |
| A | 160 | 150 |
| … | … | … |
| B | 145 | 135 |
| B | 155 | 145 |
| B | 165 | 155 |
| … | … | … |
Pertanyaannya adalah, apakah ada perbedaan signifikan dalam efektivitas kedua obat tersebut?
Langkah-langkah Penyelesaian
- Rumuskan hipotesis nol dan hipotesis alternatif.
- Hipotesis nol (H0): Tidak ada perbedaan signifikan dalam efektivitas kedua obat tersebut.
- Hipotesis alternatif (H1): Ada perbedaan signifikan dalam efektivitas kedua obat tersebut.
- Tentukan tingkat signifikansi (α). Biasanya tingkat signifikansi yang digunakan adalah 0,05.
- Hitung statistik uji t. Statistik uji t dihitung dengan rumus:
- x̄1 adalah rata-rata sampel untuk obat A
- x̄2 adalah rata-rata sampel untuk obat B
- s12 adalah varians sampel untuk obat A
- s22 adalah varians sampel untuk obat B
- n1 adalah ukuran sampel untuk obat A
- n2 adalah ukuran sampel untuk obat B
- Tentukan nilai kritis. Nilai kritis ditentukan berdasarkan tingkat signifikansi (α) dan derajat bebas (df). Derajat bebas dihitung dengan rumus:
- Bandingkan statistik uji t dengan nilai kritis. Jika statistik uji t lebih besar dari nilai kritis, maka tolak hipotesis nol. Jika statistik uji t lebih kecil dari nilai kritis, maka gagal tolak hipotesis nol.
- Buat kesimpulan. Berdasarkan hasil uji t, kita dapat menyimpulkan apakah ada perbedaan signifikan dalam efektivitas kedua obat tersebut.
t = (x̄1 – x̄2) / √(s12/n1 + s22/n2)
Dimana:
df = n1 + n2 – 2
Tabel Hasil Perhitungan
Berikut adalah tabel yang menunjukkan data, hasil perhitungan, dan kesimpulan uji t:
| Variabel | Obat A | Obat B |
|---|---|---|
| Rata-rata Sampel (x̄) | 140 | 145 |
| Varians Sampel (s2) | 100 | 120 |
| Ukuran Sampel (n) | 20 | 20 |
| Derajat Bebas (df) | 38 | 38 |
| Statistik Uji t | -2.5 | -2.5 |
| Nilai Kritis | 2.024 | 2.024 |
| Kesimpulan | Tolak H0 | Tolak H0 |
Berdasarkan hasil uji t, kita dapat menyimpulkan bahwa ada perbedaan signifikan dalam efektivitas kedua obat tersebut. Obat A lebih efektif dalam menurunkan tekanan darah dibandingkan dengan obat B.
Contoh Soal Uji t Dua Sampel Berpasangan
Uji t dua sampel berpasangan digunakan untuk membandingkan rata-rata dua populasi yang terkait atau berpasangan. Data dalam uji ini biasanya diperoleh dari pengukuran yang sama pada subjek yang sama pada dua waktu yang berbeda atau dalam dua kondisi yang berbeda. Misalnya, untuk mengukur efektivitas suatu program pelatihan, kita bisa mengukur kinerja karyawan sebelum dan sesudah pelatihan.
Contoh Soal
Sebuah perusahaan ingin menguji efektivitas program pelatihan baru untuk meningkatkan kinerja karyawan. Mereka mengambil sampel 10 karyawan dan mengukur kinerja mereka sebelum dan sesudah mengikuti program pelatihan. Data kinerja karyawan sebelum dan sesudah pelatihan disajikan dalam tabel berikut:
| Karyawan | Kinerja Sebelum Pelatihan | Kinerja Setelah Pelatihan |
|---|---|---|
| 1 | 70 | 75 |
| 2 | 65 | 72 |
| 3 | 80 | 85 |
| 4 | 75 | 80 |
| 5 | 60 | 68 |
| 6 | 78 | 82 |
| 7 | 72 | 78 |
| 8 | 85 | 90 |
| 9 | 68 | 75 |
| 10 | 70 | 76 |
Apakah program pelatihan efektif meningkatkan kinerja karyawan?
Langkah-langkah Penyelesaian
Berikut langkah-langkah untuk menyelesaikan soal uji t dua sampel berpasangan:
- Rumuskan Hipotesis
- Hipotesis nol (H0): Program pelatihan tidak berpengaruh terhadap kinerja karyawan. Rata-rata kinerja sebelum dan sesudah pelatihan sama.
- Hipotesis alternatif (Ha): Program pelatihan berpengaruh terhadap kinerja karyawan. Rata-rata kinerja setelah pelatihan lebih tinggi daripada sebelum pelatihan.
- Tentukan Tingkat Signifikansi
- Tingkat signifikansi (α) adalah probabilitas menolak hipotesis nol ketika hipotesis nol benar. Tingkat signifikansi biasanya ditetapkan sebesar 0,05.
- Hitung Statistik Uji
- Statistik uji untuk uji t dua sampel berpasangan dihitung dengan rumus berikut:
- di mana:
- d̄ adalah rata-rata selisih kinerja sebelum dan sesudah pelatihan.
- μd adalah rata-rata selisih kinerja yang diharapkan (dalam kasus ini, 0 karena kita menguji apakah ada perbedaan).
- sd adalah standar deviasi selisih kinerja.
- n adalah jumlah sampel (dalam kasus ini, 10).
t = (d̄ – μd) / (sd / √n)
- Tentukan Nilai Kritikal
- Nilai kritikal adalah nilai yang membagi daerah penolakan dari daerah penerimaan hipotesis nol. Nilai kritikal ditentukan berdasarkan tingkat signifikansi dan derajat bebas (df = n – 1).
- Buat Keputusan
- Jika statistik uji lebih besar dari nilai kritikal, maka hipotesis nol ditolak. Ini berarti bahwa program pelatihan berpengaruh terhadap kinerja karyawan.
- Jika statistik uji lebih kecil dari nilai kritikal, maka hipotesis nol tidak ditolak. Ini berarti bahwa program pelatihan tidak berpengaruh terhadap kinerja karyawan.
Hasil Perhitungan
Berdasarkan data yang diberikan, hasil perhitungan uji t dua sampel berpasangan adalah sebagai berikut:
| Variabel | Nilai |
|---|---|
| Rata-rata Selisih (d̄) | 6 |
| Standar Deviasi Selisih (sd) | 3.16 |
| Statistik Uji (t) | 6.32 |
| Derajat Bebas (df) | 9 |
| Nilai Kritikal (α = 0.05) | 1.833 |
Kesimpulan
Karena statistik uji (6.32) lebih besar dari nilai kritikal (1.833), maka hipotesis nol ditolak. Ini berarti bahwa program pelatihan berpengaruh terhadap kinerja karyawan. Dapat disimpulkan bahwa program pelatihan efektif meningkatkan kinerja karyawan.
Interpretasi Hasil Uji t
Setelah melakukan uji t, langkah selanjutnya adalah menginterpretasikan hasil yang diperoleh. Interpretasi hasil uji t bertujuan untuk menentukan apakah terdapat perbedaan yang signifikan antara dua kelompok data atau tidak. Dalam interpretasi ini, kita akan menganalisis nilai p dan statistik uji t untuk menarik kesimpulan yang valid.
Nilai p dan Statistik Uji t
Nilai p (p-value) merupakan probabilitas mendapatkan hasil yang sama atau lebih ekstrem dari hasil yang diamati, dengan asumsi hipotesis nol benar. Statistik uji t, di sisi lain, mengukur perbedaan antara dua kelompok data, diukur dalam satuan deviasi standar.
- Nilai p:
- Jika nilai p lebih kecil dari tingkat signifikansi (biasanya 0,05), maka kita menolak hipotesis nol. Artinya, terdapat bukti yang cukup kuat untuk menyatakan bahwa terdapat perbedaan yang signifikan antara dua kelompok data.
- Jika nilai p lebih besar dari tingkat signifikansi, maka kita gagal menolak hipotesis nol. Artinya, tidak terdapat bukti yang cukup kuat untuk menyatakan bahwa terdapat perbedaan yang signifikan antara dua kelompok data.
- Statistik uji t:
- Nilai statistik uji t yang besar menunjukkan bahwa terdapat perbedaan yang signifikan antara dua kelompok data.
- Nilai statistik uji t yang kecil menunjukkan bahwa terdapat sedikit perbedaan antara dua kelompok data.
Contoh Interpretasi Hasil Uji t
Misalnya, kita ingin menguji apakah terdapat perbedaan signifikan dalam skor ujian matematika antara siswa yang mengikuti program bimbingan belajar dan siswa yang tidak mengikuti program bimbingan belajar. Hasil uji t menunjukkan nilai p = 0,03 dan statistik uji t = 2,5. Berdasarkan nilai p yang lebih kecil dari 0,05, kita dapat menolak hipotesis nol dan menyimpulkan bahwa terdapat perbedaan yang signifikan dalam skor ujian matematika antara kedua kelompok siswa. Statistik uji t yang bernilai 2,5 menunjukkan bahwa perbedaan skor ujian matematika antara kedua kelompok siswa sebesar 2,5 deviasi standar.
Perbedaan Interpretasi Uji t Satu Sisi dan Dua Sisi
Uji t satu sisi dan dua sisi memiliki perbedaan dalam interpretasi hasil. Uji t satu sisi hanya menguji hipotesis nol dalam satu arah, sedangkan uji t dua sisi menguji hipotesis nol dalam kedua arah.
- Uji t satu sisi:
- Contoh: Menguji apakah skor ujian matematika siswa yang mengikuti program bimbingan belajar lebih tinggi dibandingkan siswa yang tidak mengikuti program bimbingan belajar.
- Hipotesis nol: Tidak terdapat perbedaan dalam skor ujian matematika antara kedua kelompok siswa.
- Hipotesis alternatif: Skor ujian matematika siswa yang mengikuti program bimbingan belajar lebih tinggi dibandingkan siswa yang tidak mengikuti program bimbingan belajar.
- Nilai p hanya dihitung pada satu sisi distribusi, yaitu sisi yang sesuai dengan hipotesis alternatif.
- Uji t dua sisi:
- Contoh: Menguji apakah terdapat perbedaan dalam skor ujian matematika antara siswa yang mengikuti program bimbingan belajar dan siswa yang tidak mengikuti program bimbingan belajar, tanpa menghiraukan arah perbedaannya.
- Hipotesis nol: Tidak terdapat perbedaan dalam skor ujian matematika antara kedua kelompok siswa.
- Hipotesis alternatif: Terdapat perbedaan dalam skor ujian matematika antara kedua kelompok siswa.
- Nilai p dihitung pada kedua sisi distribusi, yaitu sisi yang sesuai dengan hipotesis alternatif.
Perbedaan Uji t Satu Sampel, Dua Sampel Bebas, dan Dua Sampel Berpasangan
Uji t adalah salah satu jenis uji statistik parametrik yang digunakan untuk membandingkan rata-rata dua kelompok data. Ada tiga jenis uji t yang umum digunakan, yaitu uji t satu sampel, uji t dua sampel bebas, dan uji t dua sampel berpasangan. Ketiga jenis uji t ini memiliki tujuan dan aplikasi yang berbeda.
Uji t Satu Sampel
Uji t satu sampel digunakan untuk membandingkan rata-rata sampel dengan nilai rata-rata populasi yang diketahui. Tujuannya adalah untuk menentukan apakah ada perbedaan signifikan antara rata-rata sampel dengan nilai rata-rata populasi yang telah ditentukan.
Contoh skenario penelitian yang cocok untuk uji t satu sampel adalah:
* Sebuah perusahaan ingin mengetahui apakah rata-rata tinggi badan karyawannya berbeda secara signifikan dari rata-rata tinggi badan populasi pria dewasa di Indonesia.
* Seorang peneliti ingin mengetahui apakah rata-rata nilai ujian mahasiswa di kelasnya berbeda secara signifikan dari nilai rata-rata nasional.
Uji t Dua Sampel Bebas
Uji t dua sampel bebas digunakan untuk membandingkan rata-rata dua kelompok sampel yang independen. Tujuannya adalah untuk menentukan apakah ada perbedaan signifikan antara rata-rata kedua kelompok sampel tersebut.
Contoh skenario penelitian yang cocok untuk uji t dua sampel bebas adalah:
* Seorang peneliti ingin mengetahui apakah ada perbedaan signifikan dalam tingkat kepuasan pelanggan antara dua jenis layanan pelanggan yang berbeda.
* Sebuah perusahaan ingin mengetahui apakah ada perbedaan signifikan dalam kinerja karyawan antara dua metode pelatihan yang berbeda.
Uji t Dua Sampel Berpasangan
Uji t dua sampel berpasangan digunakan untuk membandingkan rata-rata dua kelompok sampel yang berpasangan. Tujuannya adalah untuk menentukan apakah ada perbedaan signifikan antara rata-rata kedua kelompok sampel tersebut setelah mempertimbangkan pengaruh variabel yang berpasangan.
Contoh skenario penelitian yang cocok untuk uji t dua sampel berpasangan adalah:
* Seorang peneliti ingin mengetahui apakah ada perbedaan signifikan dalam tekanan darah sebelum dan sesudah pemberian obat tertentu.
* Sebuah perusahaan ingin mengetahui apakah ada perbedaan signifikan dalam tingkat kepuasan pelanggan sebelum dan sesudah implementasi program layanan pelanggan baru.
Perbedaan Ketiga Jenis Uji t
Berikut tabel yang merangkum perbedaan ketiga jenis uji t:
| Jenis Uji t | Tujuan | Aplikasi |
|---|---|---|
| Uji t Satu Sampel | Membandingkan rata-rata sampel dengan nilai rata-rata populasi yang diketahui | Membandingkan rata-rata sampel dengan nilai standar, seperti rata-rata nasional atau target perusahaan. |
| Uji t Dua Sampel Bebas | Membandingkan rata-rata dua kelompok sampel yang independen | Membandingkan rata-rata dua kelompok yang berbeda, seperti dua kelompok pengobatan atau dua kelompok produk yang berbeda. |
| Uji t Dua Sampel Berpasangan | Membandingkan rata-rata dua kelompok sampel yang berpasangan | Membandingkan rata-rata dua pengukuran yang diambil dari subjek yang sama, seperti sebelum dan sesudah pengobatan atau sebelum dan sesudah intervensi. |
Software Statistika untuk Uji t
Uji t adalah salah satu uji statistik yang paling umum digunakan untuk membandingkan rata-rata dua kelompok data. Uji ini dapat dilakukan dengan menggunakan berbagai software statistika yang tersedia, baik yang berbayar maupun yang gratis. Software statistika ini memudahkan proses perhitungan uji t dan membantu dalam menganalisis data secara efisien.
Software Statistika yang Umum Digunakan untuk Uji t
Beberapa software statistika yang umum digunakan untuk melakukan uji t antara lain:
- SPSS (Statistical Package for the Social Sciences): SPSS adalah software statistika yang sangat populer dan banyak digunakan dalam berbagai bidang, termasuk ilmu sosial, kesehatan, dan bisnis. SPSS menyediakan berbagai fitur untuk melakukan uji t, termasuk uji t satu sampel, uji t dua sampel, dan uji t berpasangan. SPSS memiliki antarmuka yang mudah digunakan dan dilengkapi dengan dokumentasi yang lengkap, sehingga mudah dipelajari dan digunakan.
- R: R adalah bahasa pemrograman dan lingkungan software yang digunakan untuk komputasi statistik dan grafik. R adalah software yang sangat fleksibel dan dapat digunakan untuk melakukan berbagai analisis statistik, termasuk uji t. R memiliki berbagai paket yang dapat digunakan untuk melakukan uji t, seperti paket “t.test”. R cocok untuk pengguna yang memiliki pengetahuan pemrograman dan ingin memiliki kontrol yang lebih besar atas analisis data mereka.
- Microsoft Excel: Microsoft Excel adalah software spreadsheet yang umum digunakan dan memiliki beberapa fitur statistik yang dapat digunakan untuk melakukan uji t. Excel memiliki fungsi “T.TEST” yang dapat digunakan untuk melakukan uji t satu sampel, uji t dua sampel, dan uji t berpasangan. Excel cocok untuk pengguna yang membutuhkan solusi cepat dan sederhana untuk melakukan uji t pada data yang kecil.
- JMP (Statistical Discovery Software): JMP adalah software statistika yang dikembangkan oleh SAS Institute. JMP menyediakan antarmuka yang mudah digunakan dan visualisasi data yang interaktif. JMP dilengkapi dengan fitur yang memungkinkan pengguna untuk melakukan uji t dengan mudah dan cepat. JMP cocok untuk pengguna yang membutuhkan software statistika yang mudah digunakan dan memiliki fitur visualisasi yang canggih.
Langkah-langkah Melakukan Uji t Menggunakan SPSS
Sebagai contoh, berikut adalah langkah-langkah melakukan uji t menggunakan SPSS:
- Memasukkan data: Masukkan data Anda ke dalam SPSS. Pastikan data Anda telah diorganisir dengan benar dan dalam format yang sesuai.
- Memilih menu “Analyze”: Klik menu “Analyze” pada toolbar SPSS.
- Memilih “Compare Means”: Pilih “Compare Means” dari menu “Analyze”.
- Memilih “Independent-Samples T Test”: Pilih “Independent-Samples T Test” dari menu “Compare Means”.
- Memilih variabel: Pilih variabel independen dan variabel dependen Anda. Variabel independen adalah variabel yang membagi data menjadi dua kelompok, sedangkan variabel dependen adalah variabel yang ingin Anda bandingkan rata-ratanya.
- Memilih “Define Groups”: Klik tombol “Define Groups” dan tentukan nilai variabel independen yang membedakan dua kelompok data.
- Menjalankan uji t: Klik tombol “OK” untuk menjalankan uji t.
Contoh Output Hasil Uji t dari SPSS
Output hasil uji t dari SPSS akan menampilkan berbagai informasi, termasuk:
- Statistik deskriptif: Output ini menampilkan rata-rata, standar deviasi, dan jumlah data untuk setiap kelompok.
- Uji t: Output ini menampilkan statistik uji t, derajat kebebasan, nilai p, dan interval kepercayaan.
- Hasil: Output ini akan menunjukkan apakah hasil uji t signifikan atau tidak.
| Variable | Group 1 | Group 2 |
|---|---|---|
| Mean | 10.5 | 12.2 |
| Std. Deviation | 2.1 | 1.8 |
| N | 20 | 20 |
| t | df | Sig. (2-tailed) |
|---|---|---|
| -2.5 | 38 | 0.018 |
Output di atas menunjukkan bahwa nilai p untuk uji t adalah 0.018, yang kurang dari 0.05. Ini berarti bahwa hasil uji t signifikan, dan kita dapat menolak hipotesis nol. Dengan kata lain, terdapat perbedaan signifikan antara rata-rata dua kelompok data.
Penerapan Uji t dalam Penelitian
Uji t adalah salah satu metode statistik yang umum digunakan dalam penelitian untuk menguji perbedaan antara dua kelompok data. Uji t sering digunakan untuk membandingkan rata-rata dari dua kelompok, dan dapat membantu peneliti untuk menentukan apakah perbedaan tersebut signifikan secara statistik.
Contoh Penelitian
Misalnya, seorang peneliti ingin mempelajari efektivitas program baru untuk meningkatkan kemampuan membaca anak-anak. Peneliti memilih dua kelompok anak-anak secara acak, satu kelompok menerima program baru dan kelompok lainnya menerima program standar. Setelah program selesai, peneliti mengukur kemampuan membaca kedua kelompok.
Analisis Data
Peneliti kemudian dapat menggunakan uji t untuk membandingkan skor kemampuan membaca kedua kelompok. Jika hasil uji t menunjukkan perbedaan yang signifikan, peneliti dapat menyimpulkan bahwa program baru lebih efektif daripada program standar.
Keterbatasan dan Implikasi
Namun, penting untuk diingat bahwa uji t memiliki beberapa keterbatasan. Misalnya, uji t hanya dapat digunakan untuk membandingkan dua kelompok, dan asumsi-asumsi tertentu harus dipenuhi untuk memastikan hasil yang valid. Selain itu, uji t hanya menunjukkan apakah perbedaan antara dua kelompok signifikan secara statistik, tidak menunjukkan mengapa perbedaan itu terjadi.
Interpretasi Hasil
Dalam contoh penelitian ini, jika hasil uji t menunjukkan perbedaan yang signifikan, peneliti dapat menyimpulkan bahwa program baru lebih efektif daripada program standar. Namun, peneliti harus mempertimbangkan faktor-faktor lain yang mungkin berkontribusi pada perbedaan tersebut, seperti karakteristik anak-anak dalam setiap kelompok.
Kesimpulan
Secara keseluruhan, uji t adalah alat yang berguna untuk menguji perbedaan antara dua kelompok data. Namun, penting untuk memahami keterbatasan uji t dan menginterpretasikan hasilnya dengan hati-hati.
Kesimpulan
Dengan memahami prinsip-prinsip uji t, Anda dapat menganalisis data dengan lebih baik dan menarik kesimpulan yang valid. Uji t merupakan alat yang sangat berguna untuk penelitian di berbagai bidang, seperti ilmu sosial, kesehatan, dan bisnis.