Contoh soal vektor 2 dimensi dan jawabannya – Vektor 2 dimensi adalah konsep penting dalam matematika yang menggambarkan besaran yang memiliki arah dan nilai. Vektor 2 dimensi sering dijumpai dalam kehidupan sehari-hari, seperti saat kita menentukan arah dan kecepatan suatu objek. Dalam artikel ini, kita akan menjelajahi dunia vektor 2 dimensi dengan membahas pengertian, operasi, dan aplikasi praktisnya.
Siapkan diri Anda untuk memahami konsep dasar vektor 2 dimensi, mulai dari penjumlahan dan pengurangan vektor, perkalian dengan skalar, hingga menghitung panjang dan sudut vektor. Dengan contoh soal yang disertai jawaban lengkap, Anda akan lebih mudah memahami dan menguasai materi ini.
Pengertian Vektor 2 Dimensi
Vektor 2 dimensi merupakan besaran yang memiliki nilai dan arah dalam bidang datar. Dengan kata lain, vektor 2 dimensi adalah representasi visual dari suatu besaran yang memiliki arah dan besar, yang digambarkan dalam bidang dua dimensi.
Ilustrasi Vektor 2 Dimensi, Contoh soal vektor 2 dimensi dan jawabannya
Bayangkan sebuah mobil yang bergerak ke arah timur dengan kecepatan 10 km/jam. Gerakan mobil ini dapat direpresentasikan sebagai vektor 2 dimensi. Vektor ini memiliki besar 10 km/jam dan arah ke timur.
Contoh Vektor 2 Dimensi dalam Kehidupan Sehari-hari
Vektor 2 dimensi banyak ditemukan dalam kehidupan sehari-hari, seperti:
- Kecepatan angin yang bertiup dari arah tertentu.
- Gaya yang diberikan pada sebuah benda, misalnya gaya tarik gravitasi.
- Pergerakan sebuah pesawat terbang.
- Pergerakan sebuah bola yang ditendang.
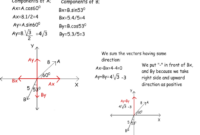
Komponen Vektor 2 Dimensi
Vektor 2 dimensi dapat diuraikan menjadi dua komponen, yaitu komponen horizontal (x) dan komponen vertikal (y). Komponen horizontal menunjukkan besarnya vektor dalam arah sumbu x, sedangkan komponen vertikal menunjukkan besarnya vektor dalam arah sumbu y.
Jenis-jenis Vektor 2 Dimensi
Vektor 2 dimensi dapat dibedakan menjadi beberapa jenis, antara lain:
- Vektor nol: Vektor yang memiliki besar 0 dan tidak memiliki arah.
- Vektor satuan: Vektor yang memiliki besar 1.
- Vektor posisi: Vektor yang menghubungkan titik asal dengan titik tertentu.
- Vektor perpindahan: Vektor yang menunjukkan perubahan posisi suatu benda.
- Vektor kecepatan: Vektor yang menunjukkan laju perubahan posisi suatu benda per satuan waktu.
- Vektor percepatan: Vektor yang menunjukkan laju perubahan kecepatan suatu benda per satuan waktu.
| Komponen Vektor 2 Dimensi | Jenis-jenis Vektor 2 Dimensi | Contoh |
|---|---|---|
| (x, y) | Vektor nol | (0, 0) |
| (x, y) | Vektor satuan | (1, 0) |
| (x, y) | Vektor posisi | (3, 4) |
| (x, y) | Vektor perpindahan | (5, -2) |
| (x, y) | Vektor kecepatan | (10, 5) |
| (x, y) | Vektor percepatan | (2, -3) |
Operasi Vektor 2 Dimensi
Setelah memahami konsep vektor 2 dimensi, selanjutnya kita akan mempelajari operasi-operasi yang dapat dilakukan pada vektor. Operasi vektor ini sangat penting dalam berbagai bidang, seperti fisika, teknik, dan ilmu komputer. Operasi dasar pada vektor 2 dimensi meliputi penjumlahan, pengurangan, dan perkalian dengan skalar.
Penjumlahan dan Pengurangan Vektor 2 Dimensi
Penjumlahan dan pengurangan vektor 2 dimensi dilakukan dengan menjumlahkan atau mengurangkan komponen-komponen yang bersesuaian. Misalkan kita memiliki dua vektor, a = (ax, ay) dan b = (bx, by), maka:
- a + b = (ax + bx, ay + by)
- a – b = (ax – bx, ay – by)
Ilustrasi penjumlahan dan pengurangan vektor dapat dilihat pada gambar berikut. Perhatikan bahwa penjumlahan vektor dapat diilustrasikan dengan aturan jajar genjang, di mana vektor hasil penjumlahan merupakan diagonal dari jajar genjang yang dibentuk oleh kedua vektor awal. Sedangkan pengurangan vektor dapat diilustrasikan dengan menghubungkan ujung vektor pertama ke ujung vektor kedua, sehingga vektor hasil pengurangan merupakan vektor yang menghubungkan titik awal vektor pertama ke ujung vektor kedua.
Gambar Ilustrasi Penjumlahan dan Pengurangan Vektor
Contoh: Misalkan a = (2, 3) dan b = (1, -1). Maka:
- a + b = (2 + 1, 3 + (-1)) = (3, 2)
- a – b = (2 – 1, 3 – (-1)) = (1, 4)
Perkalian Vektor 2 Dimensi dengan Skalar
Perkalian vektor 2 dimensi dengan skalar dilakukan dengan mengalikan setiap komponen vektor dengan skalar tersebut. Misalkan kita memiliki vektor a = (ax, ay) dan skalar k, maka:
ka = (kax, kay)
Perkalian dengan skalar akan mengubah panjang vektor, tetapi tidak mengubah arahnya. Jika skalar positif, maka panjang vektor akan bertambah. Jika skalar negatif, maka panjang vektor akan berkurang dan arahnya akan berlawanan.
Contoh: Misalkan a = (2, 3) dan k = 2. Maka:
2a = (2 * 2, 2 * 3) = (4, 6)
Rumus Operasi Vektor 2 Dimensi
Berikut tabel yang berisi rumus operasi vektor 2 dimensi dan contohnya:
| Operasi | Rumus | Contoh |
|---|---|---|
| Penjumlahan | a + b = (ax + bx, ay + by) | a = (2, 3), b = (1, -1) a + b = (2 + 1, 3 + (-1)) = (3, 2) |
| Pengurangan | a – b = (ax – bx, ay – by) | a = (2, 3), b = (1, -1) a – b = (2 – 1, 3 – (-1)) = (1, 4) |
| Perkalian dengan skalar | ka = (kax, kay) | a = (2, 3), k = 2 2a = (2 * 2, 2 * 3) = (4, 6) |
Panjang Vektor 2 Dimensi
Panjang vektor 2 dimensi merupakan nilai yang menunjukkan jarak dari titik awal vektor ke titik ujung vektor tersebut. Panjang vektor ini sering disebut dengan istilah magnitudo atau norm vektor. Menentukan panjang vektor 2 dimensi sangat penting dalam berbagai bidang seperti fisika, matematika, dan teknik, untuk memahami besaran dan arah suatu vektor.
Cara Menentukan Panjang Vektor 2 Dimensi
Untuk menentukan panjang vektor 2 dimensi, kita dapat menggunakan teorema Pythagoras. Vektor 2 dimensi dapat digambarkan sebagai garis lurus yang menghubungkan dua titik pada bidang kartesius. Garis ini membentuk sisi miring segitiga siku-siku, dengan sisi alas dan tinggi segitiga tersebut mewakili komponen vektor pada sumbu x dan sumbu y.
Latihan soal vektor 2 dimensi dan jawabannya memang membantu dalam memahami konsep, tapi jangan lupa juga untuk belajar tentang analisis break even point. Konsep ini penting untuk memahami kapan suatu bisnis mulai menghasilkan keuntungan. Kamu bisa menemukan contoh soal dan jawaban break even point dalam format pdf di situs ini.
Setelah memahami break even point, kamu bisa kembali fokus ke latihan soal vektor 2 dimensi dan jawabannya, dan menemukan aplikasi praktis dari konsep tersebut.
Misalkan kita memiliki vektor 2 dimensi v = (a, b), maka panjang vektor v dapat dihitung dengan rumus berikut:
||v|| = √(a2 + b2)
Rumus ini didapatkan dari teorema Pythagoras, dimana panjang vektor v (sisi miring) sama dengan akar kuadrat dari jumlah kuadrat komponen vektor pada sumbu x (a) dan sumbu y (b).
Langkah-langkah Menghitung Panjang Vektor 2 Dimensi
| Langkah | Contoh |
|---|---|
| 1. Tentukan komponen vektor pada sumbu x dan sumbu y. | Misalkan vektor v = (3, 4). Maka komponen vektor pada sumbu x adalah 3 dan komponen vektor pada sumbu y adalah 4. |
| 2. Kuadratkan masing-masing komponen vektor. | 32 = 9 dan 42 = 16. |
| 3. Jumlahkan hasil kuadrat dari komponen vektor. | 9 + 16 = 25. |
| 4. Akar kuadratkan hasil penjumlahan. | √25 = 5. |
| 5. Hasilnya adalah panjang vektor. | Panjang vektor v adalah 5. |
Ilustrasi Gambar Panjang Vektor 2 Dimensi
Bayangkan sebuah vektor v yang terletak di kuadran I bidang kartesius. Vektor v memiliki komponen horizontal (a) pada sumbu x dan komponen vertikal (b) pada sumbu y. Titik awal vektor berada di titik origin (0, 0) dan titik ujung vektor berada di titik (a, b). Dengan menghubungkan titik awal dan titik ujung vektor, kita membentuk sebuah segitiga siku-siku dengan sisi alas a, sisi tinggi b, dan sisi miring ||v|| yang merupakan panjang vektor v. Panjang vektor v dapat dihitung menggunakan teorema Pythagoras, yaitu ||v|| = √(a2 + b2).
Sudut Vektor 2 Dimensi
Sudut vektor 2 dimensi adalah sudut yang dibentuk oleh vektor tersebut dengan sumbu horizontal positif. Sudut ini dapat diukur dalam derajat atau radian.
Cara Menentukan Sudut Vektor 2 Dimensi
Untuk menentukan sudut vektor 2 dimensi, kita dapat menggunakan rumus trigonometri. Misalkan vektor v = (x, y) dengan x adalah komponen horizontal dan y adalah komponen vertikal. Sudut vektor v terhadap sumbu horizontal positif dapat dihitung dengan rumus:
θ = arctan (y/x)
Rumus ini didasarkan pada definisi tangen dalam trigonometri, yaitu perbandingan antara sisi depan dan sisi samping pada segitiga siku-siku. Dalam kasus ini, sisi depan adalah komponen vertikal (y) dan sisi samping adalah komponen horizontal (x).
Langkah-langkah Menghitung Sudut Vektor 2 Dimensi
Berikut adalah langkah-langkah yang dapat digunakan untuk menghitung sudut vektor 2 dimensi:
| Langkah | Contoh |
|---|---|
| 1. Tentukan komponen horizontal (x) dan komponen vertikal (y) dari vektor. | Misalkan vektor v = (3, 4) |
| 2. Hitung nilai tangen sudut dengan membagi komponen vertikal dengan komponen horizontal. | tan θ = y/x = 4/3 |
| 3. Gunakan fungsi arctangen (arctan) untuk mencari sudut θ. | θ = arctan (4/3) ≈ 53.13° |
Ilustrasi Gambar Sudut Vektor 2 Dimensi
Ilustrasi gambar berikut menunjukkan sudut vektor 2 dimensi v = (x, y) terhadap sumbu horizontal positif. Sudut θ dibentuk oleh vektor v dan sumbu horizontal positif.
[Gambar ilustrasi sudut vektor 2 dimensi]
Gambar tersebut menunjukkan bahwa sudut θ adalah sudut yang dibentuk oleh vektor v dengan sumbu horizontal positif. Sudut ini dapat dihitung dengan menggunakan rumus arctangen (arctan) dari perbandingan komponen vertikal (y) dan komponen horizontal (x) dari vektor v.
Vektor Satuan 2 Dimensi: Contoh Soal Vektor 2 Dimensi Dan Jawabannya
Vektor satuan 2 dimensi adalah vektor yang memiliki panjang 1 satuan dan arah yang sama dengan vektor aslinya. Vektor satuan penting karena dapat digunakan untuk merepresentasikan arah suatu vektor tanpa mempertimbangkan panjangnya. Vektor satuan juga berguna dalam berbagai aplikasi seperti geometri, fisika, dan pemrograman.
Cara Menentukan Vektor Satuan 2 Dimensi
Vektor satuan 2 dimensi dapat ditentukan dengan membagi vektor aslinya dengan besarnya. Rumus untuk menentukan vektor satuan adalah sebagai berikut:
Vektor Satuan (u) = Vektor Asli (v) / Besar Vektor (|v|)
Dimana:
* u adalah vektor satuan
* v adalah vektor aslinya
* |v| adalah besar vektor aslinya
Berikut adalah contoh menentukan vektor satuan 2 dimensi:
Misalkan kita memiliki vektor 2 dimensi v = (3, 4). Untuk menentukan vektor satuannya, kita perlu menghitung besar vektor v terlebih dahulu. Besar vektor v dapat dihitung dengan menggunakan teorema Pythagoras:
|v| = √(3² + 4²) = √25 = 5
Setelah kita mendapatkan besar vektor v, kita dapat menentukan vektor satuannya dengan membagi vektor v dengan besarnya:
u = v / |v| = (3, 4) / 5 = (3/5, 4/5)
Jadi, vektor satuan dari vektor v = (3, 4) adalah u = (3/5, 4/5).
Produk Skalar Vektor 2 Dimensi
Produk skalar vektor, juga dikenal sebagai perkalian dot, merupakan operasi matematika yang menghasilkan skalar (bilangan tunggal) dari dua vektor. Operasi ini memiliki aplikasi yang luas dalam berbagai bidang seperti fisika, geometri, dan ilmu komputer. Artikel ini akan membahas cara menentukan produk skalar vektor 2 dimensi, dengan disertai rumus, contoh, dan ilustrasi gambar.
Cara Menentukan Produk Skalar Vektor 2 Dimensi
Produk skalar vektor 2 dimensi dapat ditentukan dengan menggunakan rumus berikut:
a ⋅ b = (ax × bx) + (ay × by)
Dimana:
* a = vektor pertama
* b = vektor kedua
* ax = komponen x dari vektor a
* ay = komponen y dari vektor a
* bx = komponen x dari vektor b
* by = komponen y dari vektor b
Langkah-Langkah Menghitung Produk Skalar Vektor 2 Dimensi
Berikut adalah langkah-langkah yang dapat digunakan untuk menghitung produk skalar vektor 2 dimensi:
| Langkah | Contoh |
|---|---|
| Tentukan komponen x dan y dari kedua vektor. | Misalnya, vektor a = (2, 3) dan vektor b = (4, 1). Maka, ax = 2, ay = 3, bx = 4, dan by = 1. |
| Kalikan komponen x dari kedua vektor. | ax × bx = 2 × 4 = 8 |
| Kalikan komponen y dari kedua vektor. | ay × by = 3 × 1 = 3 |
| Jumlahkan hasil perkalian komponen x dan komponen y. | a ⋅ b = (ax × bx) + (ay × by) = 8 + 3 = 11 |
Ilustrasi Gambar Produk Skalar Vektor 2 Dimensi
Ilustrasi gambar produk skalar vektor 2 dimensi dapat digambarkan sebagai berikut:
* Dua vektor, a dan b, digambar pada bidang koordinat.
* Sudut θ antara kedua vektor tersebut ditunjukkan.
* Panjang proyeksi vektor a pada vektor b, yaitu ab, ditunjukkan.
* Produk skalar dari vektor a dan b sama dengan panjang proyeksi vektor a pada vektor b dikalikan dengan panjang vektor b.
a ⋅ b = |a| |b| cos θ = ab |b|
Ilustrasi ini menunjukkan bahwa produk skalar vektor dapat diinterpretasikan sebagai panjang proyeksi satu vektor pada vektor lainnya, dikalikan dengan panjang vektor kedua.
Aplikasi Vektor 2 Dimensi dalam Kehidupan Sehari-hari
Vektor 2 dimensi merupakan konsep matematika yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Vektor 2 dimensi dapat mewakili besaran yang memiliki arah dan besar, seperti kecepatan, percepatan, gaya, dan perpindahan. Dengan menggunakan vektor, kita dapat menyelesaikan berbagai masalah dalam bidang fisika, teknik, dan navigasi.
Aplikasi Vektor 2 Dimensi dalam Bidang Fisika
Dalam fisika, vektor 2 dimensi digunakan untuk menggambarkan besaran-besaran yang memiliki arah dan besar, seperti kecepatan dan percepatan. Contohnya, kecepatan mobil yang bergerak ke timur laut dapat diwakili oleh vektor yang memiliki arah ke timur laut dan besar yang sama dengan kecepatan mobil tersebut.
- Kecepatan: Kecepatan adalah perubahan posisi suatu objek dalam satuan waktu tertentu. Vektor kecepatan memiliki arah dan besar. Misalnya, sebuah mobil yang bergerak ke timur dengan kecepatan 60 km/jam dapat diwakili oleh vektor kecepatan dengan arah ke timur dan besar 60 km/jam.
- Percepatan: Percepatan adalah perubahan kecepatan suatu objek dalam satuan waktu tertentu. Vektor percepatan memiliki arah dan besar. Misalnya, sebuah mobil yang sedang melaju dan kemudian mengerem akan mengalami percepatan yang berlawanan arah dengan gerakan mobil.
Aplikasi Vektor 2 Dimensi dalam Bidang Teknik
Dalam teknik, vektor 2 dimensi digunakan untuk menggambarkan besaran-besaran yang memiliki arah dan besar, seperti gaya dan momen. Contohnya, gaya yang bekerja pada balok dapat diwakili oleh vektor yang memiliki arah yang sama dengan gaya dan besar yang sama dengan gaya tersebut.
- Gaya: Gaya adalah tarikan atau dorongan yang dapat menyebabkan perubahan gerak suatu benda. Vektor gaya memiliki arah dan besar. Misalnya, gaya gravitasi yang bekerja pada sebuah benda memiliki arah ke bawah dan besarnya sebanding dengan massa benda tersebut.
- Momen: Momen adalah kecenderungan suatu gaya untuk memutar suatu benda terhadap titik tertentu. Vektor momen memiliki arah yang tegak lurus terhadap bidang yang diputar dan besarnya sebanding dengan besar gaya dan jarak dari titik tumpu ke garis kerja gaya.
Aplikasi Vektor 2 Dimensi dalam Bidang Navigasi
Dalam navigasi, vektor 2 dimensi digunakan untuk menggambarkan arah dan jarak. Contohnya, arah dan jarak kapal yang bergerak dari satu titik ke titik lain dapat diwakili oleh vektor yang memiliki arah yang sama dengan arah perjalanan kapal dan besar yang sama dengan jarak yang ditempuh kapal.
- Arah: Arah menunjukkan ke mana suatu objek bergerak atau mengarah. Vektor arah memiliki besar 1 dan menunjukkan arah objek. Misalnya, arah utara dapat diwakili oleh vektor arah yang menunjuk ke utara.
- Jarak: Jarak menunjukkan seberapa jauh suatu objek bergerak atau berada dari titik awal. Vektor jarak memiliki besar yang sama dengan jarak yang ditempuh dan arah yang sama dengan arah gerakan objek. Misalnya, jika sebuah kapal bergerak 10 km ke timur, maka vektor jaraknya memiliki besar 10 km dan arah ke timur.
Soal Latihan Vektor 2 Dimensi
Vektor 2 dimensi adalah besaran yang memiliki nilai dan arah, yang dapat direpresentasikan dalam bidang datar. Operasi vektor 2 dimensi seperti penjumlahan, pengurangan, perkalian skalar, dan perkalian silang memiliki aplikasi luas dalam berbagai bidang seperti fisika, matematika, dan teknik.
Untuk memahami konsep vektor 2 dimensi dengan lebih baik, mari kita berlatih dengan beberapa contoh soal. Berikut adalah 5 soal latihan vektor 2 dimensi yang disertai dengan jawabannya, disusun dalam format tabel dengan kolom soal dan jawaban, dan dilengkapi ilustrasi gambar untuk setiap soal latihan.
Soal Latihan Vektor 2 Dimensi
Berikut adalah contoh soal latihan vektor 2 dimensi beserta jawabannya.
| Soal | Jawaban |
|---|---|
| Diketahui vektor a = (2, 3) dan vektor b = (1, -2). Tentukan vektor a + b! | a + b = (2, 3) + (1, -2) = (2 + 1, 3 – 2) = (3, 1) |
| Diketahui vektor a = (2, 3) dan vektor b = (1, -2). Tentukan vektor a – b! | a – b = (2, 3) – (1, -2) = (2 – 1, 3 + 2) = (1, 5) |
| Diketahui vektor a = (2, 3) dan skalar k = 2. Tentukan vektor ka! | ka = 2(2, 3) = (2 * 2, 2 * 3) = (4, 6) |
| Diketahui vektor a = (2, 3) dan vektor b = (1, -2). Tentukan hasil perkalian skalar antara vektor a dan b! | a . b = (2, 3) . (1, -2) = (2 * 1) + (3 * -2) = 2 – 6 = -4 |
| Diketahui vektor a = (2, 3) dan vektor b = (1, -2). Tentukan panjang vektor a! | |a| = √(2² + 3²) = √(4 + 9) = √13 |
Pembahasan Soal Latihan Vektor 2 Dimensi
Dalam pembahasan kali ini, kita akan membahas beberapa contoh soal latihan vektor 2 dimensi beserta langkah-langkah penyelesaiannya. Tujuannya adalah untuk membantu Anda memahami konsep vektor 2 dimensi dan mengasah kemampuan Anda dalam menyelesaikan soal-soal yang terkait dengannya.
Penjumlahan dan Pengurangan Vektor
Penjumlahan dan pengurangan vektor dapat dilakukan dengan menggunakan metode segitiga atau metode jajar genjang. Berikut adalah contoh soal dan pembahasannya:
- Diketahui vektor a = (2, 3) dan b = (-1, 4). Tentukan a + b dan a – b.
Untuk menyelesaikan soal ini, kita dapat menggunakan metode segitiga. Pertama, gambarlah vektor a dan b pada bidang kartesius. Kemudian, gambarlah vektor a + b dengan menghubungkan ujung vektor a dengan ujung vektor b. Vektor a – b dapat diperoleh dengan menghubungkan ujung vektor a dengan ujung vektor –b. Berikut ilustrasi gambarnya:
Gambar ilustrasi penjumlahan dan pengurangan vektor.
Dari gambar, kita dapat melihat bahwa:
- a + b = (2, 3) + (-1, 4) = (2 – 1, 3 + 4) = (1, 7)
- a – b = (2, 3) – (-1, 4) = (2 + 1, 3 – 4) = (3, -1)
Perkalian Vektor dengan Skalar
Perkalian vektor dengan skalar menghasilkan vektor baru yang memiliki arah yang sama atau berlawanan dengan vektor awal, tetapi dengan panjang yang berbeda. Berikut contoh soal dan pembahasannya:
- Diketahui vektor a = (3, -2) dan skalar k = 2. Tentukan 2a.
Perkalian vektor dengan skalar dapat dilakukan dengan mengalikan setiap komponen vektor dengan skalar tersebut. Dalam hal ini, 2a = 2(3, -2) = (2 * 3, 2 * -2) = (6, -4).
Hasil Kali Dot Vektor
Hasil kali dot vektor adalah operasi yang menghasilkan skalar. Hasil kali dot dua vektor dapat dihitung dengan mengalikan komponen-komponen yang sesuai dari kedua vektor dan menjumlahkannya. Berikut contoh soal dan pembahasannya:
- Diketahui vektor a = (1, 2) dan b = (3, -1). Tentukan a · b.
a · b = (1, 2) · (3, -1) = (1 * 3) + (2 * -1) = 3 – 2 = 1.
Sudut Antara Dua Vektor
Sudut antara dua vektor dapat dihitung dengan menggunakan rumus:
cos θ = (a · b) / (||a|| ||b||)
di mana θ adalah sudut antara vektor a dan b, ||a|| adalah panjang vektor a, dan ||b|| adalah panjang vektor b.
Berikut contoh soal dan pembahasannya:
- Diketahui vektor a = (2, 1) dan b = (-1, 2). Tentukan sudut antara vektor a dan b.
Pertama, kita hitung panjang vektor a dan b:
- ||a|| = √(2² + 1²) = √5
- ||b|| = √((-1)² + 2²) = √5
Kemudian, kita hitung hasil kali dot a · b:
- a · b = (2, 1) · (-1, 2) = (2 * -1) + (1 * 2) = 0
Sekarang, kita dapat menghitung sudut θ:
- cos θ = (a · b) / (||a|| ||b||) = 0 / (√5 * √5) = 0
- θ = arccos 0 = 90°
Jadi, sudut antara vektor a dan b adalah 90°.
Proyeksi Vektor
Proyeksi vektor a pada vektor b adalah vektor yang diperoleh dengan menjatuhkan garis tegak lurus dari ujung vektor a ke vektor b. Proyeksi vektor a pada vektor b dapat dihitung dengan menggunakan rumus:
projb a = ((a · b) / (||b||²)) b
Berikut contoh soal dan pembahasannya:
- Diketahui vektor a = (4, 3) dan b = (1, 2). Tentukan proyeksi vektor a pada vektor b.
Pertama, kita hitung hasil kali dot a · b dan panjang vektor b:
- a · b = (4, 3) · (1, 2) = (4 * 1) + (3 * 2) = 10
- ||b|| = √(1² + 2²) = √5
Kemudian, kita dapat menghitung proyeksi vektor a pada vektor b:
- projb a = ((a · b) / (||b||²)) b = (10 / (√5)²) (1, 2) = (2, 4)
Jadi, proyeksi vektor a pada vektor b adalah (2, 4).
Persamaan Garis
Persamaan garis dalam vektor dapat dinyatakan dalam bentuk:
r = a + tb
di mana a adalah vektor posisi titik pada garis, b adalah vektor arah garis, dan t adalah parameter skalar.
Berikut contoh soal dan pembahasannya:
- Tentukan persamaan garis yang melalui titik A(1, 2) dan sejajar dengan vektor b = (3, -1).
Vektor posisi titik A adalah a = (1, 2). Karena garis tersebut sejajar dengan vektor b, maka vektor arah garis tersebut adalah b = (3, -1). Dengan demikian, persamaan garis tersebut adalah:
- r = a + tb = (1, 2) + t(3, -1) = (1 + 3t, 2 – t)
Persamaan Bidang
Persamaan bidang dalam vektor dapat dinyatakan dalam bentuk:
r · n = a · n
di mana n adalah vektor normal bidang, a adalah vektor posisi titik pada bidang, dan r adalah vektor posisi titik sembarang pada bidang.
Berikut contoh soal dan pembahasannya:
- Tentukan persamaan bidang yang melalui titik A(2, 1, 3) dan tegak lurus dengan vektor n = (1, -2, 1).
Vektor posisi titik A adalah a = (2, 1, 3). Karena bidang tersebut tegak lurus dengan vektor n, maka vektor normal bidang tersebut adalah n = (1, -2, 1). Dengan demikian, persamaan bidang tersebut adalah:
- r · n = a · n
- (x, y, z) · (1, -2, 1) = (2, 1, 3) · (1, -2, 1)
- x – 2y + z = 2 – 2 + 3
- x – 2y + z = 3
Ringkasan Akhir
Memahami konsep vektor 2 dimensi akan membuka pintu menuju pemahaman yang lebih dalam tentang berbagai fenomena alam dan aplikasi praktisnya. Dari navigasi hingga fisika, vektor 2 dimensi berperan penting dalam berbagai bidang ilmu. Dengan latihan dan pemahaman yang baik, Anda akan siap menghadapi tantangan yang terkait dengan vektor 2 dimensi dalam dunia akademis dan kehidupan nyata.