Contoh soal x dan y – Pernahkah kamu menemukan soal matematika yang melibatkan dua variabel, x dan y, dan diminta untuk mencari nilai keduanya? Nah, itulah yang kita kenal sebagai “soal x dan y”. Soal-soal ini mungkin terlihat rumit, tapi sebenarnya memiliki konsep yang sederhana dan dapat dipahami dengan latihan yang cukup.
Dalam artikel ini, kita akan menjelajahi dunia soal x dan y, mulai dari pengertian dasar hingga berbagai jenis soal, metode penyelesaian, dan contoh soal lengkap dengan pembahasan. Kita juga akan membahas aplikasi soal x dan y dalam kehidupan sehari-hari, serta beberapa tips dan strategi untuk menguasai topik ini.
Pengertian Soal X dan Y
Dalam dunia matematika, terutama aljabar, kita sering kali menjumpai soal-soal yang melibatkan variabel “x” dan “y”. Variabel ini berfungsi sebagai representasi dari nilai yang belum diketahui, dan tujuannya adalah untuk menemukan nilai tersebut.
Definisi Soal X dan Y dalam Matematika
Soal x dan y, dalam konteks matematika, merujuk pada persamaan atau sistem persamaan yang mengandung variabel “x” dan “y”. Variabel ini mewakili besaran yang belum diketahui, dan tugas kita adalah mencari nilai-nilai “x” dan “y” yang memenuhi persamaan tersebut.
Contoh Soal X dan Y dalam Kehidupan Sehari-hari
Misalnya, kita ingin membeli 2 jenis buah, apel (x) dan jeruk (y). Harga apel Rp 5.000 per kg dan jeruk Rp 3.000 per kg. Jika kita membeli total 5 kg buah dengan harga Rp 19.000, kita dapat membentuk persamaan:
- x + y = 5 (total berat buah)
- 5000x + 3000y = 19000 (total harga buah)
Dengan menyelesaikan sistem persamaan ini, kita akan menemukan berapa kg apel (x) dan berapa kg jeruk (y) yang kita beli.
Perbedaan Soal X dan Y dengan Soal Aljabar Lainnya
Soal x dan y bukanlah satu-satunya jenis soal aljabar. Ada berbagai macam soal aljabar lainnya, seperti persamaan linear, persamaan kuadrat, dan sistem persamaan lainnya. Perbedaan utama antara soal x dan y dengan soal aljabar lainnya terletak pada jumlah variabel yang terlibat. Soal x dan y secara khusus melibatkan dua variabel, “x” dan “y”, sedangkan soal aljabar lainnya mungkin melibatkan satu variabel atau lebih dari dua variabel.
Jenis-Jenis Soal X dan Y
Soal X dan Y merupakan jenis soal yang sering dijumpai dalam berbagai bidang, mulai dari matematika hingga sains. Keduanya memiliki karakteristik dan bentuk persamaan yang berbeda, yang mempengaruhi cara penyelesaiannya. Memahami jenis-jenis soal X dan Y serta karakteristiknya dapat membantu kita dalam menyelesaikan soal dengan lebih mudah dan efektif.
Jenis Soal X
Soal X umumnya berkaitan dengan persamaan linear, yaitu persamaan yang melibatkan variabel dengan pangkat satu. Bentuk umum dari persamaan linear adalah ax + b = c, di mana a, b, dan c adalah konstanta dan x adalah variabel.
- Soal X dengan satu variabel: Jenis soal ini hanya melibatkan satu variabel, misalnya 2x + 5 = 11. Untuk menyelesaikannya, kita perlu mencari nilai x yang memenuhi persamaan tersebut.
- Soal X dengan dua variabel: Jenis soal ini melibatkan dua variabel, misalnya x + 2y = 7. Untuk menyelesaikannya, kita perlu mencari nilai x dan y yang memenuhi persamaan tersebut. Biasanya, soal ini dilengkapi dengan persamaan lain yang melibatkan variabel yang sama, sehingga kita dapat menggunakan metode eliminasi atau substitusi untuk mencari solusi.
Jenis Soal Y
Soal Y umumnya berkaitan dengan persamaan kuadrat, yaitu persamaan yang melibatkan variabel dengan pangkat dua. Bentuk umum dari persamaan kuadrat adalah ax2 + bx + c = 0, di mana a, b, dan c adalah konstanta dan x adalah variabel.
Contoh soal x dan y seringkali ditemui dalam matematika, biasanya melibatkan persamaan linear atau sistem persamaan. Nah, kalau kamu ingin mencoba soal yang lebih menantang, coba deh cari contoh soal HOTS Bahasa Inggris. Di contoh soal hots bahasa inggris kamu bisa menemukan berbagai soal yang menguji kemampuan berpikir kritis dan analisis, seperti interpretasi teks, inferensi, dan pemecahan masalah.
Setelah berlatih soal HOTS, kamu bisa kembali ke contoh soal x dan y dengan pemahaman yang lebih mendalam dan strategi yang lebih baik.
- Soal Y dengan faktorisasi: Jenis soal ini dapat diselesaikan dengan memfaktorkan persamaan kuadrat. Faktorisasi adalah proses mencari dua faktor yang jika dikalikan menghasilkan persamaan kuadrat awal. Misalnya, persamaan x2 – 4x + 3 = 0 dapat difaktorkan menjadi (x – 1)(x – 3) = 0. Dari sini, kita dapat menemukan nilai x yang memenuhi persamaan, yaitu x = 1 atau x = 3.
- Soal Y dengan rumus abc: Jenis soal ini dapat diselesaikan dengan menggunakan rumus abc, yaitu x = (-b ± √(b2 – 4ac)) / 2a. Rumus ini dapat digunakan untuk mencari nilai x yang memenuhi persamaan kuadrat, meskipun persamaan tersebut tidak dapat difaktorkan. Misalnya, persamaan 2x2 + 3x – 5 = 0 dapat diselesaikan dengan rumus abc, menghasilkan nilai x = 1 atau x = -5/2.
Metode Penyelesaian Soal X dan Y
Sistem persamaan linear dua variabel (SPLTV) merupakan persamaan yang memiliki dua variabel, biasanya dilambangkan dengan x dan y. Ada berbagai metode untuk menyelesaikan SPLTV, seperti metode substitusi, eliminasi, dan grafik. Ketiga metode ini memiliki cara kerja yang berbeda, tetapi tujuannya sama yaitu menemukan nilai x dan y yang memenuhi kedua persamaan dalam sistem tersebut.
Metode Substitusi
Metode substitusi adalah salah satu metode yang umum digunakan untuk menyelesaikan sistem persamaan linear dua variabel. Metode ini melibatkan penggantian salah satu variabel dalam salah satu persamaan dengan ekspresi yang setara dari persamaan lainnya.
- Selesaikan salah satu persamaan untuk salah satu variabel. Misalnya, selesaikan persamaan pertama untuk x.
- Substitusikan ekspresi x yang diperoleh pada langkah pertama ke dalam persamaan kedua.
- Selesaikan persamaan kedua untuk variabel y.
- Substitusikan nilai y yang diperoleh pada langkah ketiga ke dalam persamaan pertama (atau persamaan kedua) untuk menemukan nilai x.
Contoh:
x + y = 5
2x – y = 1
Langkah-langkah penyelesaian dengan metode substitusi:
- Selesaikan persamaan pertama untuk x: x = 5 – y.
- Substitusikan x = 5 – y ke dalam persamaan kedua: 2(5 – y) – y = 1.
- Selesaikan persamaan kedua untuk y: 10 – 2y – y = 1; -3y = -9; y = 3.
- Substitusikan y = 3 ke dalam persamaan pertama: x + 3 = 5; x = 2.
Jadi, solusi sistem persamaan tersebut adalah x = 2 dan y = 3.
Metode Eliminasi
Metode eliminasi adalah metode lain yang sering digunakan untuk menyelesaikan sistem persamaan linear dua variabel. Metode ini melibatkan penghapusan salah satu variabel dengan cara menjumlahkan atau mengurangkan kedua persamaan dalam sistem.
- Kalikan kedua persamaan dengan konstanta sehingga koefisien salah satu variabel sama, tetapi dengan tanda yang berlawanan.
- Jumlahkan kedua persamaan. Variabel yang memiliki koefisien sama dengan tanda berlawanan akan saling menghilangkan.
- Selesaikan persamaan yang dihasilkan untuk variabel yang tersisa.
- Substitusikan nilai variabel yang diperoleh pada langkah ketiga ke dalam salah satu persamaan awal untuk menemukan nilai variabel lainnya.
Contoh:
x + 2y = 8
3x – 2y = 4
Langkah-langkah penyelesaian dengan metode eliminasi:
- Koefisien y sudah sama tetapi dengan tanda yang berlawanan, jadi kita langsung bisa menjumlahkan kedua persamaan.
- Jumlahkan kedua persamaan: x + 2y + 3x – 2y = 8 + 4; 4x = 12.
- Selesaikan persamaan untuk x: x = 3.
- Substitusikan x = 3 ke dalam persamaan pertama: 3 + 2y = 8; 2y = 5; y = 2.5.
Jadi, solusi sistem persamaan tersebut adalah x = 3 dan y = 2.5.
Metode Grafik
Metode grafik adalah metode visual untuk menyelesaikan sistem persamaan linear dua variabel. Metode ini melibatkan menggambar grafik dari kedua persamaan dalam sistem dan mencari titik potong kedua grafik tersebut. Titik potong tersebut merupakan solusi sistem persamaan.
- Ubah kedua persamaan dalam bentuk y = mx + c, di mana m adalah gradien dan c adalah titik potong sumbu y.
- Gambar grafik dari kedua persamaan pada bidang koordinat.
- Tentukan titik potong kedua grafik. Titik potong tersebut merupakan solusi sistem persamaan.
Contoh:
x + y = 5
2x – y = 1
Langkah-langkah penyelesaian dengan metode grafik:
- Ubah kedua persamaan dalam bentuk y = mx + c: y = -x + 5 dan y = 2x – 1.
- Gambar grafik dari kedua persamaan pada bidang koordinat. Grafik pertama memiliki gradien -1 dan titik potong sumbu y 5, sedangkan grafik kedua memiliki gradien 2 dan titik potong sumbu y -1.
- Titik potong kedua grafik adalah (2, 3). Jadi, solusi sistem persamaan tersebut adalah x = 2 dan y = 3.
Metode grafik sangat membantu untuk memvisualisasikan solusi sistem persamaan. Namun, metode ini mungkin tidak selalu akurat, terutama jika titik potong kedua grafik sulit ditentukan.
Contoh Soal dan Pembahasan
Untuk memahami konsep x dan y dengan lebih baik, mari kita lihat beberapa contoh soal dan pembahasannya. Contoh soal ini akan membantu Anda untuk memahami bagaimana cara menyelesaikan persamaan linear dengan dua variabel.
Contoh Soal
Berikut adalah 3 contoh soal x dan y yang berbeda beserta pembahasannya.
| No | Soal | Langkah Penyelesaian | Jawaban |
|---|---|---|---|
| 1 | Tentukan nilai x dan y dari sistem persamaan berikut: x + 2y = 5 3x – y = 1 |
Untuk menyelesaikan sistem persamaan ini, kita dapat menggunakan metode eliminasi. Langkah pertama, kalikan persamaan pertama dengan 3 dan persamaan kedua dengan 2. 3(x + 2y) = 3(5) 2(3x – y) = 2(1) 3x + 6y = 15 Langkah kedua, eliminasi variabel y dengan menjumlahkan kedua persamaan. Langkah ketiga, selesaikan persamaan untuk x. Langkah keempat, substitusikan nilai x ke salah satu persamaan awal untuk menyelesaikan y. Langkah kelima, substitusikan nilai y ke persamaan x untuk mendapatkan nilai x. Jadi, nilai x = 1 dan y = 2. |
x = 1, y = 2 |
| 2 | Sebuah toko menjual 2 jenis kue, yaitu kue A dan kue B. Harga 1 kue A adalah Rp 10.000 dan harga 1 kue B adalah Rp 15.000. Pada suatu hari, toko tersebut menjual 50 kue dengan total pendapatan Rp 600.000. Tentukan banyaknya kue A dan kue B yang terjual. | Misalkan x adalah banyaknya kue A dan y adalah banyaknya kue B yang terjual. Diketahui: x + y = 50 (total kue terjual) 10.000x + 15.000y = 600.000 (total pendapatan) Selesaikan sistem persamaan ini dengan metode substitusi. Substitusikan nilai y ke persamaan x. Jadi, banyaknya kue A yang terjual adalah 30 dan banyaknya kue B yang terjual adalah 20. |
Kue A = 30, Kue B = 20 |
| 3 | Suatu persegi panjang memiliki panjang 5 cm lebih panjang dari lebarnya. Jika keliling persegi panjang tersebut adalah 38 cm, tentukan panjang dan lebar persegi panjang tersebut. | Misalkan lebar persegi panjang adalah x cm dan panjangnya adalah (x + 5) cm. Keliling persegi panjang adalah 2(panjang + lebar). 2(x + 5 + x) = 38 2(2x + 5) = 38 4x + 10 = 38 4x = 28 x = 7 Panjang persegi panjang adalah x + 5 = 7 + 5 = 12 cm. |
Lebar = 7 cm, Panjang = 12 cm |
Aplikasi Soal X dan Y dalam Kehidupan Sehari-hari
Soal X dan Y, yang sering dijumpai dalam pelajaran matematika, ternyata memiliki aplikasi luas dalam kehidupan sehari-hari. Kedua konsep ini menjadi alat penting dalam berbagai bidang, mulai dari ekonomi hingga fisika dan kimia.
Aplikasi dalam Bidang Ekonomi
Soal X dan Y berperan penting dalam memahami perilaku konsumen dan produsen dalam pasar. Contohnya, dalam analisis permintaan dan penawaran, soal X dan Y dapat digunakan untuk menentukan titik keseimbangan pasar, yaitu titik di mana jumlah barang yang ditawarkan sama dengan jumlah barang yang diminta.
- Soal X dapat merepresentasikan jumlah barang yang ditawarkan, sementara soal Y mewakili harga barang tersebut.
- Dengan menggunakan persamaan linear, kita dapat menentukan hubungan antara jumlah barang yang ditawarkan dan harga, serta menentukan titik keseimbangan pasar.
Aplikasi dalam Bidang Fisika
Dalam fisika, soal X dan Y sering digunakan untuk menggambarkan gerak benda, khususnya gerak lurus. Soal X dapat mewakili jarak tempuh, sementara soal Y mewakili waktu tempuh.
- Dengan menggunakan persamaan gerak, kita dapat menentukan kecepatan dan percepatan benda, serta menentukan posisi benda pada waktu tertentu.
- Contohnya, dalam kasus gerak jatuh bebas, soal X mewakili jarak jatuh, sementara soal Y mewakili waktu jatuh.
Aplikasi dalam Bidang Kimia
Soal X dan Y juga memiliki peran penting dalam kimia, khususnya dalam menentukan konsentrasi larutan. Soal X dapat mewakili jumlah zat terlarut, sementara soal Y mewakili volume larutan.
- Dengan menggunakan rumus konsentrasi, kita dapat menentukan jumlah zat terlarut dalam larutan dengan volume tertentu.
- Contohnya, dalam perhitungan molaritas larutan, soal X mewakili jumlah mol zat terlarut, sementara soal Y mewakili volume larutan dalam liter.
Soal Latihan
Setelah mempelajari tentang persamaan linear dua variabel, mari kita asah pemahaman dengan mengerjakan beberapa soal latihan berikut. Soal-soal ini dirancang dengan tingkat kesulitan yang bervariasi, mulai dari yang mudah hingga yang menantang, untuk membantu Anda menguji kemampuan dalam menyelesaikan masalah yang berkaitan dengan persamaan linear dua variabel.
Soal Latihan
Berikut adalah 5 soal latihan tentang persamaan linear dua variabel yang dapat Anda kerjakan:
- Tentukan nilai x dan y yang memenuhi sistem persamaan berikut:
2x + 3y = 7
x – y = 1 - Sebuah toko menjual dua jenis kue, yaitu kue A dan kue B. Harga satu kue A adalah Rp10.000 dan harga satu kue B adalah Rp15.000. Seorang pembeli membeli 3 kue A dan 2 kue B dengan total harga Rp60.000. Berapakah jumlah kue A dan kue B yang dibeli pembeli tersebut?
- Diketahui sistem persamaan linear berikut:
ax + by = c
dx + ey = fTentukan nilai x dan y dalam bentuk persamaan yang melibatkan a, b, c, d, e, dan f.
- Selesaikan sistem persamaan berikut dengan metode eliminasi:
3x + 2y = 11
x – 3y = -5 - Tentukan nilai x dan y yang memenuhi sistem persamaan berikut dengan metode substitusi:
x + 2y = 5
2x – y = 1
Kunci Jawaban
Berikut adalah kunci jawaban untuk soal latihan di atas:
- x = 2, y = 1
- Jumlah kue A yang dibeli adalah 2, dan jumlah kue B yang dibeli adalah 2.
-
x = (ce – bf) / (ae – bd)
y = (af – cd) / (ae – bd) - x = 2, y = 2.5
- x = 1, y = 2
Tips Mengerjakan Soal X dan Y
Pernah merasa bingung dengan soal X dan Y? Jangan khawatir, soal-soal ini sebenarnya tidak serumit yang dibayangkan. Dengan pemahaman yang tepat dan strategi yang jitu, kamu bisa menaklukkan soal X dan Y dengan mudah.
Memahami Konsep Soal X dan Y
Soal X dan Y biasanya menguji kemampuanmu dalam memecahkan masalah matematika yang melibatkan dua variabel, yaitu X dan Y. Untuk memahami konsep ini, kamu perlu memahami hubungan antara kedua variabel tersebut. Misalnya, bagaimana perubahan nilai X memengaruhi nilai Y, atau sebaliknya.
Mengidentifikasi Jenis Soal X dan Y
Ada beberapa jenis soal X dan Y, seperti persamaan linear, persamaan kuadrat, dan sistem persamaan. Untuk mengidentifikasi jenis soal dengan cepat, perhatikan bentuk persamaannya. Apakah persamaan tersebut hanya memiliki variabel X dan Y dengan pangkat satu? Jika ya, maka itu adalah persamaan linear. Jika persamaan tersebut melibatkan pangkat dua pada variabel X atau Y, maka itu adalah persamaan kuadrat. Sedangkan sistem persamaan melibatkan dua atau lebih persamaan yang memiliki variabel X dan Y.
Strategi Menyelesaikan Soal X dan Y
Berikut adalah beberapa strategi yang bisa kamu gunakan untuk menyelesaikan soal X dan Y:
- Substitusi: Cara ini melibatkan penggantian nilai satu variabel dengan nilai variabel lainnya. Misalnya, jika kamu punya persamaan X + Y = 5 dan X = 2, maka kamu bisa mengganti X dengan 2 dalam persamaan pertama, sehingga diperoleh 2 + Y = 5. Dengan demikian, nilai Y dapat dihitung yaitu 3.
- Eliminasi: Strategi ini melibatkan eliminasi satu variabel dengan cara menjumlahkan atau mengurangkan kedua persamaan. Misalnya, jika kamu punya persamaan X + Y = 5 dan X – Y = 1, maka dengan menjumlahkan kedua persamaan tersebut, kamu akan mendapatkan 2X = 6. Dengan demikian, nilai X dapat dihitung yaitu 3.
- Grafik: Cara ini melibatkan penggambaran kedua persamaan pada satu diagram. Titik potong antara kedua grafik tersebut merupakan solusi dari sistem persamaan.
- Rumus: Beberapa soal X dan Y dapat diselesaikan dengan menggunakan rumus tertentu. Misalnya, untuk menyelesaikan persamaan kuadrat, kamu bisa menggunakan rumus kuadrat.
Tips Tambahan
- Latihan: Semakin banyak kamu berlatih, semakin mahir kamu dalam menyelesaikan soal X dan Y.
- Memahami Konsep Dasar: Pastikan kamu memahami konsep dasar matematika yang berkaitan dengan soal X dan Y, seperti persamaan, variabel, dan sistem persamaan.
- Manfaatkan Sumber Belajar: Jangan ragu untuk memanfaatkan buku, website, atau tutor untuk mendapatkan bantuan dalam memahami konsep dan menyelesaikan soal X dan Y.
Kesalahan Umum dalam Menyelesaikan Soal X dan Y
Soal x dan y seringkali muncul dalam berbagai ujian, baik akademik maupun profesional. Meskipun terlihat sederhana, banyak orang yang melakukan kesalahan dalam menyelesaikannya. Kesalahan-kesalahan ini bisa disebabkan oleh kurangnya pemahaman konsep, kurangnya latihan, atau bahkan kecerobohan dalam membaca soal. Artikel ini akan membahas beberapa kesalahan umum yang sering dilakukan dalam menyelesaikan soal x dan y, beserta penyebab dan contoh soalnya.
Mencampuradukkan Konsep, Contoh soal x dan y
Salah satu kesalahan umum yang sering dilakukan adalah mencampuradukkan konsep. Misalnya, dalam menyelesaikan soal x dan y yang melibatkan persamaan linear, siswa mungkin salah menerapkan rumus atau konsep yang digunakan untuk persamaan kuadrat. Hal ini bisa terjadi karena kurangnya pemahaman konsep dasar atau kurangnya latihan dalam menyelesaikan soal serupa.
- Contoh Soal: Tentukan nilai x dan y yang memenuhi sistem persamaan berikut:
x + 2y = 5
2x – y = 1
Penyelesaian yang salah: Beberapa siswa mungkin mencoba menyelesaikan sistem persamaan ini dengan menggunakan rumus kuadrat, yang tidak tepat karena sistem persamaan ini merupakan persamaan linear.
Kesalahan dalam Operasi Aritmatika
Kesalahan dalam operasi aritmatika juga sering terjadi dalam menyelesaikan soal x dan y. Hal ini bisa disebabkan oleh kecerobohan dalam menghitung, kurangnya ketelitian, atau kurangnya pemahaman tentang aturan operasi matematika. Kesalahan ini bisa berakibat fatal, karena dapat menyebabkan hasil yang salah.
- Contoh Soal: Tentukan nilai x dan y yang memenuhi sistem persamaan berikut:
x + 3y = 7
2x – y = 1
Penyelesaian yang salah: Dalam menyelesaikan persamaan, siswa mungkin salah menghitung hasil operasi penjumlahan atau pengurangan, sehingga nilai x dan y yang diperoleh menjadi salah.
Kesalahan dalam Mengidentifikasi Variabel
Dalam menyelesaikan soal x dan y, penting untuk mengidentifikasi variabel dengan benar. Kesalahan dalam mengidentifikasi variabel bisa terjadi karena kurangnya pemahaman tentang konteks soal atau kurangnya ketelitian dalam membaca soal. Kesalahan ini dapat menyebabkan kesalahan dalam menyelesaikan persamaan.
- Contoh Soal: Sebuah toko menjual dua jenis kue, kue A dan kue B. Kue A dijual dengan harga Rp 10.000 per potong, sedangkan kue B dijual dengan harga Rp 15.000 per potong. Seorang pembeli membeli 3 potong kue A dan 2 potong kue B dengan total harga Rp 60.000. Tentukan banyaknya kue A dan kue B yang dibeli.
Penyelesaian yang salah: Siswa mungkin salah mengidentifikasi variabel x dan y. Misalnya, siswa mendefinisikan x sebagai banyaknya kue A dan y sebagai banyaknya kue B, tetapi kemudian salah menggunakan variabel tersebut dalam persamaan.
Kesalahan dalam Menginterpretasikan Hasil
Setelah menyelesaikan persamaan, penting untuk menginterpretasikan hasil dengan benar. Kesalahan dalam menginterpretasikan hasil bisa terjadi karena kurangnya pemahaman tentang konteks soal atau kurangnya ketelitian dalam memeriksa hasil. Kesalahan ini dapat menyebabkan kesimpulan yang salah.
- Contoh Soal: Tentukan nilai x dan y yang memenuhi sistem persamaan berikut:
x + y = 5
x – y = 1
Penyelesaian yang salah: Setelah menyelesaikan persamaan, siswa mungkin salah menginterpretasikan hasil. Misalnya, siswa memperoleh nilai x = 3 dan y = 2, tetapi kemudian salah menyimpulkan bahwa x mewakili banyaknya kue A dan y mewakili banyaknya kue B.
Tidak Memeriksa Kembali Hasil
Salah satu kesalahan umum yang sering dilakukan adalah tidak memeriksa kembali hasil. Hal ini bisa disebabkan oleh kurangnya waktu, kurangnya ketelitian, atau kurangnya kesadaran akan pentingnya memeriksa hasil. Memeriksa kembali hasil dapat membantu menemukan kesalahan yang mungkin terjadi dalam proses penyelesaian.
- Contoh Soal: Tentukan nilai x dan y yang memenuhi sistem persamaan berikut:
x + 2y = 5
2x – y = 1
Penyelesaian yang salah: Setelah menyelesaikan persamaan, siswa mungkin tidak memeriksa kembali hasil. Hal ini dapat menyebabkan kesalahan yang tidak terdeteksi, sehingga hasil yang diperoleh menjadi salah.
Sumber Belajar Soal X dan Y: Contoh Soal X Dan Y
Bagi yang sedang belajar tentang soal X dan Y, menemukan sumber belajar yang tepat sangat penting untuk memahami konsep dan mengasah kemampuan dalam menyelesaikan soal-soal. Berikut beberapa rekomendasi sumber belajar yang bisa membantu kamu:
Buku Teks
Buku teks merupakan sumber belajar yang terpercaya dan komprehensif. Berikut beberapa buku teks yang membahas soal X dan Y secara detail:
- “Judul Buku 1” oleh [Penulis 1] – Buku ini membahas konsep X dan Y dengan pendekatan yang mudah dipahami dan dilengkapi dengan contoh soal yang beragam.
- “Judul Buku 2” oleh [Penulis 2] – Buku ini menyajikan materi X dan Y secara sistematis dan dilengkapi dengan latihan soal yang menantang.
- “Judul Buku 3” oleh [Penulis 3] – Buku ini fokus pada aplikasi praktis X dan Y dalam kehidupan sehari-hari, dilengkapi dengan studi kasus dan contoh nyata.
Website dan Platform Online
Website dan platform online menyediakan akses mudah ke berbagai materi belajar, termasuk soal latihan dan pembahasan. Berikut beberapa platform online yang bisa kamu gunakan:
- [Nama Website 1] – Platform ini menyediakan latihan soal X dan Y dengan tingkat kesulitan yang beragam, dilengkapi dengan pembahasan yang lengkap.
- [Nama Website 2] – Platform ini menyediakan materi belajar X dan Y dalam bentuk video tutorial, artikel, dan kuis interaktif.
- [Nama Website 3] – Platform ini menawarkan forum diskusi yang memungkinkan kamu untuk berinteraksi dengan pengguna lain dan berbagi pengetahuan tentang X dan Y.
Video Tutorial
Video tutorial dapat membantu kamu memahami konsep X dan Y secara visual dan interaktif. Berikut beberapa channel YouTube yang membahas soal X dan Y secara detail:
- [Nama Channel YouTube 1] – Channel ini menyediakan video tutorial yang jelas dan mudah dipahami, dilengkapi dengan contoh soal dan pembahasan.
- [Nama Channel YouTube 2] – Channel ini menawarkan video tutorial yang kreatif dan menarik, dengan pendekatan yang interaktif dan menyenangkan.
- [Nama Channel YouTube 3] – Channel ini menyediakan video tutorial yang fokus pada aplikasi praktis X dan Y dalam berbagai bidang.
Tantangan dalam Menyelesaikan Soal X dan Y
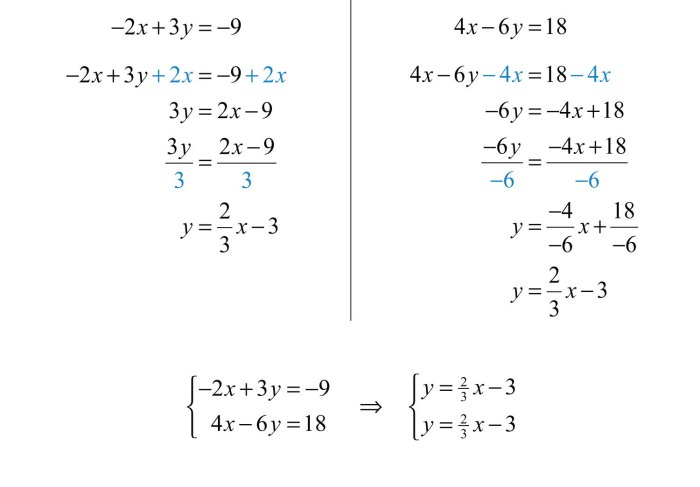
Menyelesaikan soal X dan Y, khususnya dalam konteks matematika dan fisika, seringkali menghadirkan tantangan tersendiri. Tantangan ini bisa muncul dari berbagai faktor, mulai dari pemahaman konsep yang kurang mendalam hingga kesulitan dalam mengaplikasikan rumus dan strategi penyelesaian yang tepat. Untuk membantu Anda menaklukkan tantangan ini, mari kita bahas beberapa poin penting yang perlu diperhatikan.
Memahami Konsep Dasar
Salah satu tantangan utama dalam menyelesaikan soal X dan Y adalah memahami konsep dasar yang mendasari soal tersebut. Tanpa pemahaman yang kuat, akan sulit untuk menentukan langkah penyelesaian yang tepat. Contohnya, dalam soal fisika, pemahaman tentang hukum Newton sangat penting untuk menyelesaikan soal yang melibatkan gerak benda.
- Pastikan Anda memahami definisi, rumus, dan prinsip-prinsip dasar yang terkait dengan topik yang dibahas dalam soal.
- Pelajari contoh-contoh soal yang serupa untuk mendapatkan pemahaman yang lebih baik tentang bagaimana konsep-konsep tersebut diterapkan.
- Jangan ragu untuk bertanya kepada guru atau teman sekelas jika Anda mengalami kesulitan dalam memahami konsep tertentu.
Mengidentifikasi Jenis Soal
Tantangan berikutnya adalah mengidentifikasi jenis soal yang Anda hadapi. Soal X dan Y bisa dibedakan berdasarkan beberapa kriteria, seperti tingkat kesulitan, jenis operasi yang terlibat, dan konsep yang diuji. Kemampuan untuk mengidentifikasi jenis soal dengan tepat akan membantu Anda memilih strategi penyelesaian yang paling efektif.
- Perhatikan kata kunci dan frasa yang digunakan dalam soal. Kata-kata seperti “hitung”, “tentukan”, “buktikan”, atau “jelaskan” dapat memberikan petunjuk tentang jenis soal yang Anda hadapi.
- Perhatikan struktur dan format soal. Apakah soal tersebut berbentuk persamaan, grafik, atau tabel?
- Perhatikan data yang diberikan dalam soal. Data apa yang relevan dengan konsep yang diuji?
Menentukan Strategi Penyelesaian
Setelah memahami konsep dasar dan mengidentifikasi jenis soal, langkah selanjutnya adalah menentukan strategi penyelesaian yang tepat. Strategi ini bisa berupa langkah-langkah yang sistematis, rumus-rumus yang relevan, atau teknik-teknik khusus yang berlaku untuk jenis soal tertentu.
- Buatlah kerangka penyelesaian yang sistematis. Misalnya, dalam soal fisika, Anda bisa menggunakan langkah-langkah berikut: (1) identifikasi konsep yang terlibat, (2) tuliskan rumus yang relevan, (3) masukkan data yang diberikan, (4) selesaikan persamaan, dan (5) tuliskan jawaban akhir.
- Perhatikan unit dan dimensi yang digunakan dalam soal. Kesalahan dalam penggunaan unit dapat menyebabkan kesalahan dalam jawaban akhir.
- Jika Anda menemukan kesulitan dalam menentukan strategi penyelesaian, coba konsultasikan dengan guru atau teman sekelas Anda.
Menghindari Kesalahan Umum
Terakhir, penting untuk menghindari kesalahan umum yang sering terjadi dalam menyelesaikan soal X dan Y. Kesalahan ini bisa berupa kesalahan hitung, kesalahan interpretasi, atau kesalahan dalam mengaplikasikan rumus.
- Periksa kembali jawaban Anda dengan teliti. Pastikan Anda tidak melakukan kesalahan hitung atau kesalahan dalam memasukkan data.
- Perhatikan unit dan dimensi yang digunakan dalam soal. Kesalahan dalam penggunaan unit dapat menyebabkan kesalahan dalam jawaban akhir.
- Jika Anda merasa ragu dengan jawaban Anda, coba selesaikan soal tersebut dengan cara yang berbeda. Jika Anda mendapatkan jawaban yang sama, maka kemungkinan besar jawaban Anda benar.
Contoh Soal
“Sebuah mobil bergerak dengan kecepatan 20 m/s. Jika mobil tersebut mengerem dengan perlambatan 5 m/s², berapa jarak yang ditempuh mobil hingga berhenti?”
Soal ini merupakan contoh soal yang melibatkan konsep gerak lurus berubah beraturan (GLBB). Untuk menyelesaikan soal ini, Anda perlu memahami konsep GLBB, rumus yang relevan, dan cara mengaplikasikannya.
Pentingnya Mempelajari Soal X dan Y
Dalam dunia pendidikan, mempelajari soal X dan Y memiliki peran yang penting dalam membentuk kemampuan berpikir logis dan analitis. Soal X dan Y, yang biasanya melibatkan konsep-konsep matematika dan logika, merupakan alat yang efektif untuk melatih otak dalam menyelesaikan masalah secara sistematis dan terstruktur.
Manfaat Mempelajari Soal X dan Y dalam Meningkatkan Kemampuan Berpikir Logis
Mempelajari soal X dan Y secara intensif dapat membantu dalam meningkatkan kemampuan berpikir logis dengan beberapa cara. Soal-soal ini memaksa kita untuk berpikir kritis, menganalisis informasi, dan mencari solusi yang tepat berdasarkan logika. Dengan berlatih memecahkan soal X dan Y, kita akan terbiasa dengan proses berpikir deduktif dan induktif, yang penting dalam menyelesaikan masalah kompleks.
- Melatih kemampuan analisis dan pemecahan masalah: Soal X dan Y seringkali melibatkan analisis data, identifikasi pola, dan penerapan logika untuk menemukan solusi. Proses ini melatih kemampuan berpikir analitis dan pemecahan masalah secara sistematis.
- Meningkatkan kemampuan berpikir kritis: Dalam menyelesaikan soal X dan Y, kita dituntut untuk mengevaluasi informasi, mengidentifikasi asumsi, dan merumuskan argumen yang logis. Hal ini membantu dalam mengembangkan kemampuan berpikir kritis yang penting dalam berbagai aspek kehidupan.
- Mengembangkan kemampuan abstraksi: Soal X dan Y seringkali melibatkan konsep-konsep abstrak yang memerlukan pemahaman dan kemampuan untuk berpikir secara umum. Melalui latihan, kita dapat mengembangkan kemampuan abstraksi yang membantu dalam memahami dan memecahkan masalah yang kompleks.
Peran Soal X dan Y dalam Memecahkan Masalah Sehari-hari
Kemampuan berpikir logis yang diasah melalui mempelajari soal X dan Y memiliki aplikasi praktis dalam kehidupan sehari-hari. Dalam berbagai situasi, kita seringkali dihadapkan pada masalah yang memerlukan pendekatan logis dan analitis untuk menemukan solusi yang tepat.
- Pengambilan keputusan: Dalam berbagai situasi, kita harus membuat keputusan yang tepat berdasarkan informasi yang tersedia. Kemampuan berpikir logis membantu dalam menganalisis pilihan, mempertimbangkan konsekuensi, dan membuat keputusan yang rasional.
- Memecahkan masalah teknis: Soal X dan Y seringkali melibatkan konsep-konsep matematika dan logika yang dapat diterapkan dalam memecahkan masalah teknis. Misalnya, dalam bidang teknik, ilmu komputer, atau keuangan, kemampuan berpikir logis dan analitis sangat diperlukan.
- Komunikasi yang efektif: Kemampuan berpikir logis membantu dalam merumuskan argumen yang jelas dan koheren, serta memahami sudut pandang orang lain. Hal ini penting dalam komunikasi yang efektif, baik dalam lingkungan profesional maupun personal.
Aplikasi Soal X dan Y dalam Bidang Pekerjaan
Kemampuan berpikir logis yang diasah melalui mempelajari soal X dan Y sangat dihargai dalam berbagai bidang pekerjaan. Dalam banyak profesi, kemampuan ini menjadi aset penting untuk menyelesaikan tugas, berkolaborasi dengan rekan kerja, dan mencapai tujuan organisasi.
- Bidang sains dan teknologi: Ilmuwan, teknisi, dan pengembang perangkat lunak membutuhkan kemampuan berpikir logis untuk merumuskan hipotesis, menganalisis data, dan memecahkan masalah teknis.
- Bidang bisnis dan keuangan: Analis keuangan, manajer, dan pengusaha membutuhkan kemampuan berpikir logis untuk membuat keputusan bisnis, menganalisis pasar, dan mengelola risiko.
- Bidang hukum dan pemerintahan: Pengacara, hakim, dan pejabat pemerintah membutuhkan kemampuan berpikir logis untuk menganalisis kasus, merumuskan argumen, dan membuat keputusan yang adil.
Pemungkas
Memahami soal x dan y tidak hanya penting untuk meraih nilai bagus dalam pelajaran matematika, tapi juga untuk mengembangkan kemampuan berpikir logis dan memecahkan masalah dalam berbagai situasi. Dengan memahami konsep dasar, menguasai metode penyelesaian, dan rajin berlatih, kamu akan dapat menaklukkan soal x dan y dengan mudah.