Fungsi eksponen dan logaritma contoh soal – Pernahkah Anda bertanya-tanya bagaimana pertumbuhan populasi, peluruhan radioaktif, atau bunga majemuk dihitung? Di balik fenomena-fenomena tersebut, terdapat konsep matematika yang menarik, yaitu fungsi eksponen dan logaritma. Fungsi eksponen dan logaritma merupakan dua konsep penting dalam matematika yang memiliki peran vital dalam berbagai bidang, mulai dari ilmu pengetahuan hingga kehidupan sehari-hari.
Dalam artikel ini, kita akan menjelajahi dunia fungsi eksponen dan logaritma, mempelajari definisinya, sifat-sifatnya, dan hubungan timbal balik di antara keduanya. Selain itu, kita akan melihat contoh-contoh soal yang akan membantu Anda memahami konsep ini dengan lebih baik. Siap untuk menjelajahi dunia fungsi eksponen dan logaritma? Mari kita mulai!
Pengertian Fungsi Logaritma
Fungsi logaritma merupakan fungsi invers dari fungsi eksponen. Fungsi logaritma menjawab pertanyaan: “Pangkat berapa yang harus diberikan pada suatu bilangan pokok agar hasilnya sama dengan suatu bilangan tertentu?”. Misalnya, logaritma dari 100 dengan basis 10 adalah 2, karena 10 pangkat 2 sama dengan 100. Secara umum, logaritma dari suatu bilangan y dengan basis b adalah x jika dan hanya jika b pangkat x sama dengan y.
Persamaan fungsi logaritma ditulis sebagai:
logby = x jika dan hanya jika bx = y
di mana:
- b adalah basis logaritma (b > 0 dan b ≠ 1)
- y adalah bilangan yang dicari logaritmanya (y > 0)
- x adalah logaritma dari y dengan basis b
Perbedaan Fungsi Logaritma dan Fungsi Eksponen
Berikut tabel yang berisi perbedaan antara fungsi logaritma dan fungsi eksponen:
| Aspek | Fungsi Logaritma | Fungsi Eksponen |
|---|---|---|
| Rumus | logby = x jika dan hanya jika bx = y | y = bx |
| Basis | b > 0 dan b ≠ 1 | b > 0 dan b ≠ 1 |
| Domain | y > 0 | x ∈ R |
| Range | x ∈ R | y > 0 |
| Grafik | Memotong sumbu x di titik (1, 0) dan memiliki asimtot vertikal di garis x = 0 | Memotong sumbu y di titik (0, 1) dan memiliki asimtot horizontal di garis y = 0 |
| Sifat | logb1 = 0, logbb = 1, logb(xy) = logbx + logby, logb(x/y) = logbx – logby, logbxn = n logbx | b0 = 1, b1 = b, bm * bn = bm+n, bm / bn = bm-n, (bm)n = bmn |
Karakteristik Grafik Fungsi Logaritma
Grafik fungsi logaritma memiliki karakteristik utama sebagai berikut:
- Memotong sumbu x di titik (1, 0): Artinya, untuk setiap basis logaritma, logaritma dari 1 selalu bernilai 0.
- Memiliki asimtot vertikal di garis x = 0: Artinya, grafik fungsi logaritma mendekati garis x = 0 tetapi tidak pernah menyentuhnya.
- Grafik fungsi logaritma selalu naik jika basisnya lebih besar dari 1: Ini berarti semakin besar nilai x, semakin besar nilai logaritma dari x.
- Grafik fungsi logaritma selalu turun jika basisnya lebih kecil dari 1: Ini berarti semakin besar nilai x, semakin kecil nilai logaritma dari x.
Sifat Fungsi Eksponen: Fungsi Eksponen Dan Logaritma Contoh Soal
Fungsi eksponen memiliki sifat-sifat khusus yang memudahkan kita dalam menyelesaikan persamaan dan masalah yang melibatkan fungsi ini. Sifat-sifat ini merupakan hasil dari definisi fungsi eksponen itu sendiri, yaitu perkalian berulang dari suatu bilangan dengan dirinya sendiri.
Sifat Perkalian
Sifat perkalian fungsi eksponen menyatakan bahwa perkalian dua fungsi eksponen dengan basis yang sama menghasilkan fungsi eksponen baru dengan basis yang sama dan pangkat yang merupakan penjumlahan dari kedua pangkat semula.
am * an = am+n
Contohnya, jika kita memiliki 23 * 24, maka kita dapat menggunakan sifat perkalian ini untuk menghitungnya:
23 * 24 = 23+4 = 27
Sifat Pembagian
Sifat pembagian fungsi eksponen menyatakan bahwa pembagian dua fungsi eksponen dengan basis yang sama menghasilkan fungsi eksponen baru dengan basis yang sama dan pangkat yang merupakan selisih dari kedua pangkat semula.
am / an = am-n
Contohnya, jika kita memiliki 35 / 32, maka kita dapat menggunakan sifat pembagian ini untuk menghitungnya:
35 / 32 = 35-2 = 33
Sifat Pangkat
Sifat pangkat fungsi eksponen menyatakan bahwa pangkat dari fungsi eksponen menghasilkan fungsi eksponen baru dengan basis yang sama dan pangkat yang merupakan hasil perkalian dari kedua pangkat semula.
(am)n = am*n
Contohnya, jika kita memiliki (52)3, maka kita dapat menggunakan sifat pangkat ini untuk menghitungnya:
(52)3 = 52*3 = 56
Penerapan Sifat Fungsi Eksponen dalam Penyelesaian Soal
Sifat-sifat fungsi eksponen yang telah kita bahas sangat berguna dalam menyelesaikan persamaan eksponen. Contohnya, perhatikan persamaan eksponen berikut:
2x * 2x+1 = 32
Kita dapat menggunakan sifat perkalian untuk menyederhanakan persamaan ini:
2x * 2x+1 = 2x + (x+1) = 22x+1
Kemudian, kita dapat mengubah 32 menjadi bentuk eksponen dengan basis 2:
32 = 25
Sekarang, persamaan kita menjadi:
22x+1 = 25
Karena basisnya sama, kita dapat menyamakan pangkatnya:
2x + 1 = 5
Selanjutnya, kita dapat menyelesaikan persamaan linear ini:
2x = 4
x = 2
Jadi, solusi dari persamaan eksponen 2x * 2x+1 = 32 adalah x = 2.
Langkah-Langkah dalam Menyelesaikan Persamaan Eksponen
Berikut adalah diagram alur yang menggambarkan langkah-langkah dalam menyelesaikan persamaan eksponen:
[Gambar diagram alur yang menggambarkan langkah-langkah dalam menyelesaikan persamaan eksponen. Diagram alur ini menunjukkan langkah-langkah mulai dari identifikasi persamaan eksponen, menyederhanakan persamaan menggunakan sifat-sifat fungsi eksponen, menyelesaikan persamaan, dan memverifikasi solusi.]
Diagram alur ini menunjukkan langkah-langkah umum dalam menyelesaikan persamaan eksponen. Namun, langkah-langkah spesifik dapat bervariasi tergantung pada bentuk persamaan eksponen yang diberikan.
Sifat Fungsi Logaritma
Fungsi logaritma merupakan fungsi invers dari fungsi eksponen. Artinya, jika kita memiliki persamaan eksponen y = a^x, maka fungsi logaritma yang bersesuaian adalah x = log_a y. Fungsi logaritma memiliki beberapa sifat yang penting untuk dipahami dalam menyelesaikan persamaan dan masalah yang melibatkan logaritma.
Sifat Perkalian
Sifat perkalian logaritma menyatakan bahwa logaritma dari hasil perkalian dua bilangan sama dengan jumlah logaritma kedua bilangan tersebut. Secara matematis, dapat ditulis sebagai:
log_a (x * y) = log_a x + log_a y
Contoh:
log_2 (8 * 16) = log_2 8 + log_2 16 = 3 + 4 = 7
Sifat Pembagian
Sifat pembagian logaritma menyatakan bahwa logaritma dari hasil pembagian dua bilangan sama dengan selisih logaritma kedua bilangan tersebut. Secara matematis, dapat ditulis sebagai:
log_a (x / y) = log_a x – log_a y
Contoh:
log_3 (27 / 9) = log_3 27 – log_3 9 = 3 – 2 = 1
Sifat Pangkat
Sifat pangkat logaritma menyatakan bahwa logaritma dari suatu bilangan yang dipangkatkan dengan suatu angka sama dengan hasil kali pangkat tersebut dengan logaritma bilangan tersebut. Secara matematis, dapat ditulis sebagai:
log_a (x^n) = n * log_a x
Contoh:
log_5 (25^3) = 3 * log_5 25 = 3 * 2 = 6
Contoh Penerapan Sifat Fungsi Logaritma
Misalnya, kita ingin menyelesaikan persamaan logaritma berikut:
log_2 (x^2 + 3x) = log_2 (2x + 6)
Untuk menyelesaikan persamaan ini, kita dapat menggunakan sifat perkalian logaritma:
log_2 (x^2 + 3x) = log_2 (2x + 6)
log_2 (x(x + 3)) = log_2 (2(x + 3))
Kemudian, kita dapat menyederhanakan persamaan tersebut:
x(x + 3) = 2(x + 3)
Selanjutnya, kita dapat menyelesaikan persamaan kuadrat tersebut:
x^2 + x – 6 = 0
(x + 3)(x – 2) = 0
Maka, solusi dari persamaan logaritma tersebut adalah x = -3 atau x = 2.
Langkah-langkah Menyelesaikan Persamaan Logaritma
Berikut adalah diagram alur yang menggambarkan langkah-langkah dalam menyelesaikan persamaan logaritma:
| Langkah | Keterangan |
|---|---|
| 1. Ubah persamaan logaritma menjadi bentuk eksponen. | Gunakan definisi logaritma untuk mengubah persamaan logaritma menjadi bentuk eksponen. |
| 2. Sederhanakan persamaan eksponen. | Sederhanakan persamaan eksponen dengan menggunakan sifat-sifat eksponen. |
| 3. Selesaikan persamaan eksponen. | Selesaikan persamaan eksponen dengan menggunakan metode aljabar yang sesuai. |
| 4. Verifikasi solusi. | Pastikan solusi yang diperoleh memenuhi persamaan logaritma awal. |
Dengan memahami sifat-sifat fungsi logaritma, kita dapat menyelesaikan persamaan dan masalah yang melibatkan logaritma dengan lebih mudah.
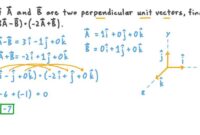
Hubungan Fungsi Eksponen dan Logaritma
Fungsi eksponen dan fungsi logaritma merupakan dua konsep matematika yang saling berhubungan erat. Keduanya memiliki peran penting dalam berbagai bidang, seperti ilmu komputer, fisika, dan ekonomi. Memahami hubungan timbal balik antara kedua fungsi ini akan memperkaya pemahaman kita tentang sifat dan aplikasi mereka.
Hubungan Timbal Balik Fungsi Eksponen dan Logaritma
Fungsi eksponen dan logaritma merupakan fungsi invers satu sama lain. Artinya, jika kita memiliki sebuah fungsi eksponen, maka fungsi logaritma dengan basis yang sama dapat “membalikkan” proses eksponen tersebut, dan sebaliknya. Hubungan ini dapat diilustrasikan dengan persamaan berikut:
Jika y = ax, maka x = logay
Persamaan ini menunjukkan bahwa jika kita memiliki nilai y yang diperoleh dari fungsi eksponen dengan basis a dan eksponen x, maka kita dapat memperoleh nilai x dengan menggunakan fungsi logaritma dengan basis a dan nilai y.
Contohnya, jika kita memiliki fungsi eksponen y = 23, maka nilai y adalah 8. Untuk mendapatkan nilai x, kita dapat menggunakan fungsi logaritma dengan basis 2: x = log28. Hasilnya adalah x = 3, yang sama dengan eksponen pada fungsi eksponen awal.
Contoh Soal
Berikut adalah contoh soal yang melibatkan hubungan antara fungsi eksponen dan logaritma:
Diketahui persamaan eksponen y = 5x. Tentukan nilai x jika y = 125.
Penyelesaian:
Kita dapat menyelesaikan soal ini dengan menggunakan fungsi logaritma dengan basis 5:
x = log5125
Karena 53 = 125, maka x = 3.
Ilustrasi Grafik
Ilustrasi grafik berikut menunjukkan hubungan antara fungsi eksponen dan logaritma:
[Gambar grafik fungsi eksponen dan logaritma dengan basis yang sama, menunjukkan bahwa kedua fungsi tersebut merupakan refleksi satu sama lain terhadap garis y = x]
Grafik fungsi eksponen dan logaritma dengan basis yang sama merupakan refleksi satu sama lain terhadap garis y = x. Hal ini menunjukkan bahwa kedua fungsi tersebut saling invers.
Penerapan Fungsi Eksponen dalam Kehidupan Sehari-hari
Fungsi eksponen memiliki peran penting dalam memahami berbagai fenomena alam dan kehidupan sehari-hari. Fungsi ini memungkinkan kita untuk memodelkan dan memprediksi pertumbuhan, peluruhan, dan perubahan yang terjadi secara eksponensial. Dalam artikel ini, kita akan menjelajahi beberapa contoh konkret penerapan fungsi eksponen dalam berbagai bidang kehidupan.
Fungsi eksponen dan logaritma memang sering dijumpai dalam berbagai aplikasi matematika, termasuk dalam soal-soal ekonomi. Misalnya, dalam menentukan harga keseimbangan pasar, fungsi eksponen dan logaritma dapat digunakan untuk memodelkan hubungan antara permintaan dan penawaran. Nah, untuk memahami lebih lanjut mengenai aplikasi fungsi eksponen dan logaritma dalam ekonomi, coba lihat contoh soal harga keseimbangan pasar yang dibahas di situs ini.
Dengan memahami konsep-konsep dasar fungsi eksponen dan logaritma, kamu akan lebih mudah menyelesaikan berbagai macam soal, termasuk soal-soal ekonomi yang melibatkan penentuan harga keseimbangan pasar.
Pertumbuhan Penduduk
Pertumbuhan penduduk merupakan salah satu contoh klasik penerapan fungsi eksponen. Seiring waktu, populasi manusia cenderung meningkat secara eksponensial, dengan laju pertumbuhan yang semakin cepat. Model pertumbuhan eksponensial dapat digunakan untuk memprediksi jumlah penduduk di masa depan, dengan mempertimbangkan faktor-faktor seperti tingkat kelahiran, kematian, dan migrasi.
- Misalnya, jika suatu negara memiliki tingkat pertumbuhan penduduk sebesar 2% per tahun, maka jumlah penduduknya akan meningkat dua kali lipat dalam waktu sekitar 35 tahun. Rumus yang digunakan untuk menghitung pertumbuhan penduduk adalah:
P(t) = P0(1 + r)t
di mana P(t) adalah jumlah penduduk setelah t tahun, P0 adalah jumlah penduduk awal, dan r adalah tingkat pertumbuhan penduduk.
Peluruhan Radioaktif
Peluruhan radioaktif adalah proses di mana inti atom yang tidak stabil melepaskan energi dan partikel subatomik, sehingga berubah menjadi atom yang lebih stabil. Proses peluruhan ini terjadi secara eksponensial, dengan waktu paruh yang konstan. Waktu paruh adalah waktu yang dibutuhkan untuk jumlah inti atom radioaktif berkurang menjadi setengahnya.
- Contohnya, waktu paruh karbon-14 adalah sekitar 5.730 tahun. Ini berarti bahwa setiap 5.730 tahun, jumlah karbon-14 dalam suatu sampel akan berkurang menjadi setengahnya. Rumus yang digunakan untuk menghitung peluruhan radioaktif adalah:
N(t) = N0(1/2)t/T
di mana N(t) adalah jumlah inti atom radioaktif setelah t tahun, N0 adalah jumlah inti atom radioaktif awal, dan T adalah waktu paruh.
Bunga Majemuk
Bunga majemuk adalah bunga yang dihitung tidak hanya pada pokok pinjaman atau investasi, tetapi juga pada bunga yang telah terkumpul sebelumnya. Bunga majemuk menghasilkan pertumbuhan eksponensial, karena bunga yang diperoleh setiap periode akan ditambahkan ke pokok, sehingga menghasilkan bunga yang lebih besar di periode berikutnya.
- Rumus yang digunakan untuk menghitung bunga majemuk adalah:
A = P(1 + r/n)nt
di mana A adalah jumlah total setelah t tahun, P adalah pokok, r adalah suku bunga tahunan, n adalah jumlah kali bunga dihitung per tahun, dan t adalah waktu dalam tahun.
Contoh Penerapan Fungsi Eksponen dalam Berbagai Bidang
| Bidang | Contoh Penerapan Fungsi Eksponen |
|---|---|
| Biologi | Pertumbuhan populasi bakteri, penyebaran penyakit menular |
| Kimia | Reaksi kimia, laju reaksi |
| Fisika | Peluruhan radioaktif, getaran harmonik |
| Ekonomi | Pertumbuhan ekonomi, inflasi |
| Teknik | Analisis sirkuit listrik, desain sistem kontrol |
Bagaimana Fungsi Eksponen Membantu Memahami Fenomena Pertumbuhan dan Peluruhan?
Fungsi eksponen memberikan cara yang tepat untuk memodelkan dan memprediksi fenomena pertumbuhan dan peluruhan yang terjadi secara eksponensial. Dengan menggunakan fungsi eksponen, kita dapat menentukan laju pertumbuhan atau peluruhan, waktu paruh, dan nilai akhir setelah periode tertentu.
Contohnya, dalam pertumbuhan penduduk, fungsi eksponen memungkinkan kita untuk memprediksi jumlah penduduk di masa depan, dengan mempertimbangkan tingkat pertumbuhan yang konstan. Dalam peluruhan radioaktif, fungsi eksponen memungkinkan kita untuk menghitung waktu yang dibutuhkan untuk jumlah inti atom radioaktif berkurang menjadi setengahnya. Dengan memahami fungsi eksponen, kita dapat memperoleh pemahaman yang lebih dalam tentang berbagai fenomena alam dan kehidupan sehari-hari.
Penerapan Fungsi Logaritma dalam Kehidupan Sehari-hari
Fungsi logaritma, meskipun tampak rumit, memiliki peran penting dalam kehidupan sehari-hari. Logaritma memungkinkan kita untuk memahami dan mengukur fenomena yang memiliki skala sangat luas, mulai dari intensitas suara hingga tingkat keasaman. Dalam berbagai bidang, logaritma memberikan cara yang efisien untuk mewakili dan menganalisis data yang memiliki rentang nilai yang sangat besar.
Skala pH
Skala pH digunakan untuk mengukur keasaman atau kebasaan suatu larutan. Skala ini berkisar dari 0 hingga 14, dengan nilai 7 menunjukkan larutan netral. Nilai pH yang lebih rendah dari 7 menunjukkan larutan asam, sedangkan nilai pH yang lebih tinggi dari 7 menunjukkan larutan basa. Skala pH didasarkan pada fungsi logaritma, di mana setiap perubahan satu satuan pH mewakili perubahan sepuluh kali lipat dalam konsentrasi ion hidrogen.
Contohnya, larutan dengan pH 4 memiliki konsentrasi ion hidrogen sepuluh kali lebih tinggi daripada larutan dengan pH 5. Penggunaan skala logaritma memungkinkan kita untuk mewakili rentang konsentrasi ion hidrogen yang sangat luas dengan skala yang lebih mudah dipahami.
Skala Richter
Skala Richter digunakan untuk mengukur kekuatan gempa bumi. Skala ini juga didasarkan pada fungsi logaritma, di mana setiap peningkatan satu satuan pada skala Richter mewakili peningkatan sepuluh kali lipat dalam amplitudo gelombang seismik.
Contohnya, gempa bumi dengan magnitudo 6 pada skala Richter memiliki amplitudo gelombang seismik sepuluh kali lebih besar daripada gempa bumi dengan magnitudo 5. Skala logaritma memungkinkan kita untuk membandingkan kekuatan gempa bumi yang sangat bervariasi dengan cara yang mudah dipahami.
Pengukuran Intensitas Suara
Intensitas suara diukur dalam desibel (dB). Skala desibel juga menggunakan fungsi logaritma, di mana setiap peningkatan 10 dB mewakili peningkatan sepuluh kali lipat dalam intensitas suara.
Contohnya, suara bisikan memiliki intensitas sekitar 30 dB, sedangkan suara mesin jet memiliki intensitas sekitar 120 dB. Penggunaan skala logaritma memungkinkan kita untuk mewakili rentang intensitas suara yang sangat luas dengan skala yang lebih mudah dipahami.
Tabel Penerapan Fungsi Logaritma
| Bidang | Penerapan | Contoh |
|---|---|---|
| Kimia | Skala pH | Larutan asam, basa, dan netral |
| Geofisika | Skala Richter | Kekuatan gempa bumi |
| Fisika | Pengukuran intensitas suara | Suara bisikan, suara mesin jet |
| Biologi | Pertumbuhan populasi | Model pertumbuhan eksponensial |
| Ekonomi | Pertumbuhan investasi | Perhitungan bunga majemuk |
Fungsi logaritma memainkan peran penting dalam memahami dan menganalisis berbagai fenomena skala dan intensitas. Dalam berbagai bidang seperti kimia, geofisika, fisika, biologi, dan ekonomi, logaritma memberikan cara yang efisien untuk mewakili dan menganalisis data yang memiliki rentang nilai yang sangat besar.
Contoh Soal Fungsi Eksponen
Fungsi eksponen adalah fungsi yang memiliki variabel di eksponennya. Fungsi eksponen memiliki berbagai macam aplikasi di berbagai bidang seperti matematika, fisika, ekonomi, dan biologi. Contohnya, pertumbuhan populasi, peluruhan radioaktif, dan bunga majemuk dapat dimodelkan menggunakan fungsi eksponen.
Contoh Soal 1: Operasi Dasar Fungsi Eksponen
Contoh soal pertama ini akan mengilustrasikan operasi dasar pada fungsi eksponen, seperti penjumlahan, pengurangan, perkalian, dan pembagian.
Misalkan kita memiliki dua fungsi eksponen, yaitu:
- f(x) = 2x
- g(x) = 3x
Tentukan nilai dari:
- f(2) + g(1)
- f(3) – g(2)
- f(1) * g(2)
- f(4) / g(3)
Berikut langkah-langkah penyelesaiannya:
- f(2) + g(1) = 22 + 31 = 4 + 3 = 7
- f(3) – g(2) = 23 – 32 = 8 – 9 = -1
- f(1) * g(2) = 21 * 32 = 2 * 9 = 18
- f(4) / g(3) = 24 / 33 = 16 / 27
Contoh Soal 2: Soal Menantang Fungsi Eksponen
Contoh soal kedua ini akan menguji pemahaman lebih dalam tentang fungsi eksponen dan melibatkan beberapa konsep penting, seperti persamaan eksponen dan sifat-sifat eksponen.
Misalkan kita memiliki persamaan eksponen berikut:
2x+1 + 2x = 12
Tentukan nilai x yang memenuhi persamaan tersebut.
Berikut langkah-langkah penyelesaiannya:
- Sederhanakan persamaan dengan memanipulasi eksponennya. Kita bisa menulis 2x+1 sebagai 2 * 2x. Sehingga persamaan menjadi: 2 * 2x + 2x = 12
- Gabungkan suku-suku yang memiliki basis yang sama: 3 * 2x = 12
- Bagi kedua ruas dengan 3: 2x = 4
- Tulis 4 sebagai 22: 2x = 22
- Karena basisnya sama, maka eksponennya juga harus sama: x = 2
Jadi, nilai x yang memenuhi persamaan tersebut adalah 2.
Contoh Soal Fungsi Logaritma
Fungsi logaritma merupakan fungsi invers dari fungsi eksponen. Fungsi logaritma digunakan untuk mencari eksponen yang diperlukan untuk mencapai suatu nilai tertentu dengan menggunakan basis tertentu.
Contoh Soal Fungsi Logaritma
Contoh soal berikut melibatkan berbagai operasi pada fungsi logaritma, seperti penjumlahan, pengurangan, perkalian, dan pembagian.
Misalnya, kita ingin mencari nilai dari
log2 16 + log2 8 – log2 4
Berikut langkah-langkah penyelesaiannya:
- Gunakan sifat logaritma:
loga b + loga c = loga (b * c)
dan
loga b – loga c = loga (b / c)
Maka, soal tersebut dapat diubah menjadi:
log2 (16 * 8) – log2 4 = log2 128 – log2 4
- Gunakan sifat logaritma:
loga bn = n * loga b
Maka, soal tersebut dapat diubah menjadi:
log2 128 – log2 4 = log2 27 – log2 22 = 7 * log2 2 – 2 * log2 2
- Gunakan sifat logaritma:
loga a = 1
Maka, soal tersebut dapat diselesaikan:
7 * log2 2 – 2 * log2 2 = 7 * 1 – 2 * 1 = 5
Jadi, nilai dari log2 16 + log2 8 – log2 4 adalah 5.
Contoh Soal Menantang Fungsi Logaritma, Fungsi eksponen dan logaritma contoh soal
Contoh soal ini membutuhkan pemahaman mendalam tentang fungsi logaritma dan sifat-sifatnya.
Selesaikan persamaan berikut:
log3 (x + 2) + log3 (x – 1) = 2
Berikut langkah-langkah penyelesaiannya:
- Gunakan sifat logaritma:
loga b + loga c = loga (b * c)
Maka, soal tersebut dapat diubah menjadi:
log3 [(x + 2) * (x – 1)] = 2
- Ubah persamaan logaritma menjadi persamaan eksponen:
loga b = c ⇔ ac = b
Maka, soal tersebut dapat diubah menjadi:
32 = (x + 2) * (x – 1)
- Selesaikan persamaan kuadrat:
9 = x2 + x – 2
x2 + x – 11 = 0
Gunakan rumus abc untuk menyelesaikan persamaan kuadrat:
x = (-b ± √(b2 – 4ac)) / 2a
Dengan a = 1, b = 1, dan c = -11, maka:
x = (-1 ± √(12 – 4 * 1 * -11)) / 2 * 1
x = (-1 ± √(45)) / 2
x = (-1 ± 3√5) / 2
Jadi, solusi dari persamaan tersebut adalah:
x = (-1 + 3√5) / 2
dan
x = (-1 – 3√5) / 2
Ringkasan Terakhir
Fungsi eksponen dan logaritma merupakan alat yang ampuh untuk memahami berbagai fenomena di sekitar kita. Dengan memahami konsep dasar dan sifat-sifatnya, kita dapat menyelesaikan berbagai masalah dan menganalisis berbagai situasi yang melibatkan pertumbuhan, peluruhan, dan skala. Jadi, jangan ragu untuk mempelajari lebih lanjut tentang fungsi eksponen dan logaritma, dan temukan keajaiban matematika yang tersembunyi di dalamnya!