Contoh soal barisan aritmatika dan geometri – Mempelajari barisan aritmatika dan geometri bisa terasa menyenangkan, lho! Bayangkan, kamu bisa memprediksi nilai suatu pola dengan mudah. Misalnya, jika kamu menabung dengan jumlah yang sama setiap bulan, kamu bisa mengetahui berapa total tabunganmu di akhir tahun. Atau, jika kamu ingin menghitung pertumbuhan bakteri yang membelah diri, kamu bisa menggunakan konsep barisan geometri.
Pada artikel ini, kita akan menjelajahi lebih dalam tentang barisan aritmatika dan geometri, mulai dari pengertian, rumus, contoh soal, hingga aplikasi dalam kehidupan sehari-hari. Siap untuk mengasah kemampuan matematika dan memahami konsep barisan yang menarik ini?
Pengertian Barisan Aritmatika dan Geometri
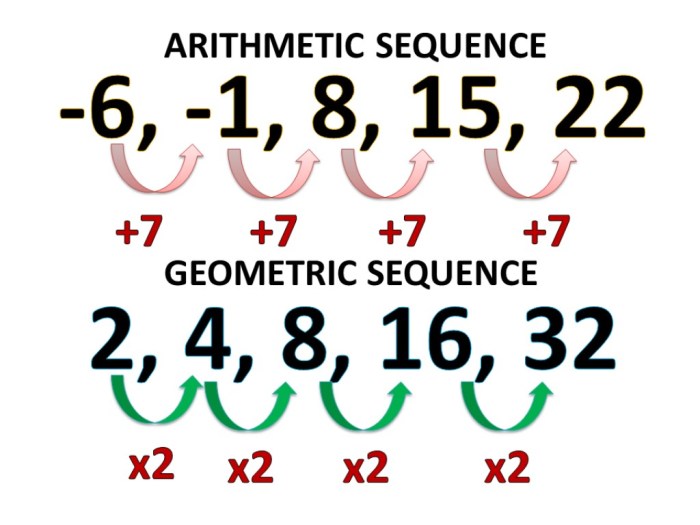
Dalam matematika, barisan adalah urutan angka yang tersusun menurut pola tertentu. Ada berbagai jenis barisan, dua di antaranya yang paling umum adalah barisan aritmetika dan barisan geometri. Kedua barisan ini memiliki karakteristik yang berbeda dan sering muncul dalam berbagai bidang seperti ilmu pengetahuan, teknologi, dan ekonomi.
Barisan Aritmetika
Barisan aritmetika adalah barisan bilangan yang memiliki selisih yang sama antara dua suku yang berurutan. Selisih ini disebut dengan beda.
Contoh sederhana dari barisan aritmetika adalah 2, 4, 6, 8, 10. Dalam barisan ini, bedanya adalah 2, karena setiap suku diperoleh dengan menambahkan 2 ke suku sebelumnya.
Barisan Geometri
Barisan geometri adalah barisan bilangan yang memiliki rasio yang sama antara dua suku yang berurutan. Rasio ini disebut dengan faktor pengali.
Contoh sederhana dari barisan geometri adalah 1, 2, 4, 8, 16. Dalam barisan ini, faktor pengalinya adalah 2, karena setiap suku diperoleh dengan mengalikan 2 ke suku sebelumnya.
Perbedaan Barisan Aritmetika dan Geometri
| Ciri | Barisan Aritmetika | Barisan Geometri |
|---|---|---|
| Selisih/Rasio | Selisih yang sama (beda) | Rasio yang sama (faktor pengali) |
| Rumus Umum | Un = a + (n-1)d | Un = a * r^(n-1) |
| Contoh | 2, 4, 6, 8, 10 | 1, 2, 4, 8, 16 |
Rumus Umum Barisan Aritmatika dan Geometri
Setelah memahami definisi dan ciri-ciri barisan aritmatika dan geometri, kita akan mempelajari rumus umum untuk menentukan suku ke-n pada kedua jenis barisan ini. Rumus umum ini sangat berguna untuk menentukan suku-suku selanjutnya dalam barisan tanpa harus menghitung secara manual dari suku awal.
Rumus Umum Suku ke-n Barisan Aritmatika
Rumus umum suku ke-n barisan aritmatika digunakan untuk menghitung nilai suku tertentu dalam barisan tanpa harus menghitung setiap suku sebelumnya. Rumus ini didasarkan pada pola penjumlahan yang konstan (beda) pada setiap suku.
Un = a + (n – 1)b
Contoh soal barisan aritmatika dan geometri sering kita temui dalam pembelajaran matematika. Selain itu, kamu juga bisa menemukan soal-soal menarik yang berkaitan dengan konsep kemiringan, seperti contoh soal kemiringan lereng yang bisa kamu pelajari di situs ini. Soal-soal tentang kemiringan lereng ini dapat dikaitkan dengan barisan aritmatika atau geometri, sehingga melatih kemampuanmu dalam memecahkan masalah matematika secara lebih kompleks.
Keterangan:
- Un = Suku ke-n
- a = Suku pertama
- n = Nomor urut suku
- b = Beda (selisih antara dua suku berurutan)
Contoh Penerapan Rumus Umum Barisan Aritmatika
Misalnya, kita memiliki barisan aritmatika: 2, 5, 8, 11, …
Tentukan suku ke-10 dari barisan tersebut.
Diketahui:
- a = 2
- b = 5 – 2 = 3
- n = 10
Maka, suku ke-10 (U10) dapat dihitung dengan rumus:
U10 = a + (n – 1)b
U10 = 2 + (10 – 1)3
U10 = 2 + 9 * 3
U10 = 2 + 27
U10 = 29
Jadi, suku ke-10 dari barisan aritmatika 2, 5, 8, 11, … adalah 29.
Rumus Umum Suku ke-n Barisan Geometri
Rumus umum suku ke-n barisan geometri digunakan untuk menghitung nilai suku tertentu dalam barisan tanpa harus menghitung setiap suku sebelumnya. Rumus ini didasarkan pada pola perkalian yang konstan (rasio) pada setiap suku.
Un = a * r^(n-1)
Keterangan:
- Un = Suku ke-n
- a = Suku pertama
- n = Nomor urut suku
- r = Rasio (perbandingan antara dua suku berurutan)
Contoh Penerapan Rumus Umum Barisan Geometri
Misalnya, kita memiliki barisan geometri: 3, 6, 12, 24, …
Tentukan suku ke-7 dari barisan tersebut.
Diketahui:
- a = 3
- r = 6 / 3 = 2
- n = 7
Maka, suku ke-7 (U7) dapat dihitung dengan rumus:
U7 = a * r^(n-1)
U7 = 3 * 2^(7-1)
U7 = 3 * 2^6
U7 = 3 * 64
U7 = 192
Jadi, suku ke-7 dari barisan geometri 3, 6, 12, 24, … adalah 192.
Menentukan Suku ke-n Barisan Aritmatika dan Geometri
Setelah memahami konsep dasar barisan aritmatika dan geometri, langkah selanjutnya adalah menentukan suku ke-n dari suatu barisan. Suku ke-n merujuk pada nilai suatu suku tertentu dalam barisan berdasarkan posisinya. Misalnya, suku ke-5 adalah nilai suku yang berada pada posisi kelima dalam barisan tersebut. Untuk menentukan suku ke-n, kita dapat menggunakan rumus umum yang telah dirumuskan berdasarkan pola yang ada dalam barisan tersebut.
Menentukan Suku ke-n Barisan Aritmatika
Rumus umum untuk menentukan suku ke-n (Un) pada barisan aritmatika adalah:
Un = a + (n – 1)b
Keterangan:
- Un = suku ke-n
- a = suku pertama
- b = beda
- n = posisi suku
Contoh soal:
Suatu barisan aritmatika memiliki suku pertama 3 dan beda 2. Tentukan suku ke-10 barisan tersebut!
Penyelesaian:
- Diketahui a = 3 dan b = 2.
- Tentukan suku ke-10 (n = 10).
- Gunakan rumus Un = a + (n – 1)b.
- U10 = 3 + (10 – 1)2 = 3 + 18 = 21.
- Jadi, suku ke-10 dari barisan aritmatika tersebut adalah 21.
Contoh Soal Menantang Barisan Aritmatika, Contoh soal barisan aritmatika dan geometri
Suatu barisan aritmatika memiliki suku ke-3 = 11 dan suku ke-7 = 23. Tentukan suku pertama dan beda dari barisan tersebut!
Penyelesaian:
- Diketahui U3 = 11 dan U7 = 23.
- Gunakan rumus Un = a + (n – 1)b untuk kedua suku yang diketahui.
- U3 = a + (3 – 1)b = a + 2b = 11
- U7 = a + (7 – 1)b = a + 6b = 23
- Kita peroleh dua persamaan dengan dua variabel. Selesaikan sistem persamaan tersebut.
- Dari persamaan U3, kita dapat memperoleh a = 11 – 2b.
- Substitusikan nilai a ke persamaan U7: (11 – 2b) + 6b = 23.
- Selesaikan persamaan tersebut: 4b = 12, sehingga b = 3.
- Substitusikan nilai b = 3 ke persamaan a = 11 – 2b: a = 11 – 2(3) = 5.
- Jadi, suku pertama (a) dari barisan aritmatika tersebut adalah 5 dan beda (b) adalah 3.
Menentukan Suku ke-n Barisan Geometri
Rumus umum untuk menentukan suku ke-n (Un) pada barisan geometri adalah:
Un = a * r^(n-1)
Keterangan:
- Un = suku ke-n
- a = suku pertama
- r = rasio
- n = posisi suku
Contoh soal:
Suatu barisan geometri memiliki suku pertama 2 dan rasio 3. Tentukan suku ke-6 barisan tersebut!
Penyelesaian:
- Diketahui a = 2 dan r = 3.
- Tentukan suku ke-6 (n = 6).
- Gunakan rumus Un = a * r^(n-1).
- U6 = 2 * 3^(6-1) = 2 * 3^5 = 2 * 243 = 486.
- Jadi, suku ke-6 dari barisan geometri tersebut adalah 486.
Contoh Soal Menantang Barisan Geometri
Suatu barisan geometri memiliki suku ke-2 = 12 dan suku ke-5 = 96. Tentukan suku pertama dan rasio dari barisan tersebut!
Penyelesaian:
- Diketahui U2 = 12 dan U5 = 96.
- Gunakan rumus Un = a * r^(n-1) untuk kedua suku yang diketahui.
- U2 = a * r^(2-1) = a * r = 12
- U5 = a * r^(5-1) = a * r^4 = 96
- Kita peroleh dua persamaan dengan dua variabel. Selesaikan sistem persamaan tersebut.
- Bagi persamaan U5 dengan persamaan U2: (a * r^4) / (a * r) = 96 / 12.
- Selesaikan persamaan tersebut: r^3 = 8, sehingga r = 2.
- Substitusikan nilai r = 2 ke persamaan a * r = 12: a * 2 = 12, sehingga a = 6.
- Jadi, suku pertama (a) dari barisan geometri tersebut adalah 6 dan rasio (r) adalah 2.
Penerapan Rumus Umum dalam Kehidupan Sehari-hari
Rumus umum untuk menentukan suku ke-n barisan aritmatika dan geometri dapat diterapkan dalam berbagai situasi kehidupan sehari-hari. Berikut beberapa contohnya:
- Menghitung jumlah tabungan: Jika Anda menabung dengan jumlah yang sama setiap bulan, maka jumlah tabungan Anda akan membentuk barisan aritmatika. Rumus umum dapat digunakan untuk menghitung total tabungan Anda setelah jangka waktu tertentu.
- Menghitung pertumbuhan populasi: Jika populasi suatu daerah meningkat dengan persentase yang sama setiap tahun, maka pertumbuhan populasi tersebut akan membentuk barisan geometri. Rumus umum dapat digunakan untuk memprediksi jumlah populasi di masa depan.
- Menghitung bunga majemuk: Bunga majemuk dihitung berdasarkan jumlah pokok dan bunga yang telah diperoleh sebelumnya. Proses ini membentuk barisan geometri. Rumus umum dapat digunakan untuk menghitung total bunga yang diperoleh setelah jangka waktu tertentu.
Menentukan Jumlah n Suku Pertama Barisan Aritmatika dan Geometri: Contoh Soal Barisan Aritmatika Dan Geometri
Dalam mempelajari barisan aritmatika dan geometri, kita tidak hanya perlu memahami pola suku-suku dalam barisan tersebut, tetapi juga dapat menghitung jumlah dari n suku pertama. Hal ini sangat berguna dalam berbagai aplikasi, seperti menghitung total keuntungan suatu bisnis selama beberapa tahun atau menghitung total jarak yang ditempuh oleh sebuah benda yang bergerak dengan kecepatan konstan.
Rumus Jumlah n Suku Pertama Barisan Aritmatika
Jumlah n suku pertama barisan aritmatika dapat dihitung dengan menggunakan rumus berikut:
Sn = n/2 (2a + (n-1)b)
Keterangan:
- Sn adalah jumlah n suku pertama
- a adalah suku pertama
- b adalah beda
- n adalah banyaknya suku
Rumus Jumlah n Suku Pertama Barisan Geometri
Rumus untuk menghitung jumlah n suku pertama barisan geometri adalah:
Sn = a(1-r^n) / (1-r)
Keterangan:
- Sn adalah jumlah n suku pertama
- a adalah suku pertama
- r adalah rasio
- n adalah banyaknya suku
Contoh Soal Menentukan Jumlah n Suku Pertama Barisan Aritmatika
Misalnya, kita ingin mencari jumlah 10 suku pertama dari barisan aritmatika 2, 5, 8, 11, … .
Langkah-langkah penyelesaiannya adalah:
- Tentukan suku pertama (a) = 2
- Tentukan beda (b) = 5 – 2 = 3
- Tentukan banyaknya suku (n) = 10
- Substitusikan nilai a, b, dan n ke dalam rumus Sn = n/2 (2a + (n-1)b)
- Maka, Sn = 10/2 (2(2) + (10-1)3) = 5 (4 + 27) = 5 (31) = 155
Jadi, jumlah 10 suku pertama dari barisan aritmatika 2, 5, 8, 11, … adalah 155.
Contoh Soal Menentukan Jumlah n Suku Pertama Barisan Geometri
Contohnya, kita ingin mencari jumlah 5 suku pertama dari barisan geometri 3, 6, 12, 24, … .
Langkah-langkah penyelesaiannya adalah:
- Tentukan suku pertama (a) = 3
- Tentukan rasio (r) = 6/3 = 2
- Tentukan banyaknya suku (n) = 5
- Substitusikan nilai a, r, dan n ke dalam rumus Sn = a(1-r^n) / (1-r)
- Maka, Sn = 3(1-2^5) / (1-2) = 3(-31) / (-1) = 93
Jadi, jumlah 5 suku pertama dari barisan geometri 3, 6, 12, 24, … adalah 93.
Ringkasan Terakhir
Setelah mempelajari contoh soal barisan aritmatika dan geometri, kamu pasti sudah lebih memahami bagaimana kedua konsep ini bekerja. Dengan memahami konsep dan rumus yang ada, kamu dapat menyelesaikan berbagai masalah yang berkaitan dengan pola bilangan. Barisan aritmatika dan geometri tidak hanya menarik secara teoritis, tetapi juga memiliki aplikasi praktis dalam berbagai bidang, seperti ekonomi, keuangan, dan ilmu pengetahuan. Selamat mencoba!





