Pernahkah Anda bertanya-tanya mengapa tinggi badan manusia, skor ujian, atau bahkan ukuran sepatu cenderung mengikuti pola tertentu? Itulah keajaiban distribusi normal, sebuah konsep statistik yang mendasari banyak fenomena di dunia nyata. Distribusi normal, yang juga dikenal sebagai kurva lonceng, menggambarkan bagaimana data terdistribusi secara merata di sekitar nilai tengahnya. Dalam artikel ini, kita akan menjelajahi contoh soal distribusi normal dan penyelesaiannya, serta mengungkap bagaimana konsep ini berperan penting dalam berbagai bidang seperti ilmu pengetahuan, teknik, dan bahkan kehidupan sehari-hari.
Distribusi normal adalah alat yang ampuh untuk memahami dan menganalisis data. Dengan mempelajari contoh soal distribusi normal dan penyelesaiannya, kita dapat memahami bagaimana data terdistribusi, menghitung probabilitas, dan membuat prediksi berdasarkan pola yang muncul. Artikel ini akan membahas berbagai aspek distribusi normal, mulai dari definisi dan sifat-sifatnya hingga penerapannya dalam berbagai bidang. Mari kita selami dunia distribusi normal dan temukan bagaimana konsep ini membantu kita memahami data dan membuat keputusan yang lebih baik.
Pengertian Distribusi Normal
Distribusi normal, juga dikenal sebagai kurva lonceng, merupakan salah satu distribusi probabilitas yang paling umum dan penting dalam statistika. Distribusi ini menggambarkan bagaimana data terdistribusi secara alami dalam berbagai fenomena, baik dalam ilmu pengetahuan, teknik, maupun sosial.
Contoh soal distribusi normal dan penyelesaiannya biasanya melibatkan perhitungan probabilitas suatu nilai berada dalam rentang tertentu. Misalnya, mencari probabilitas tinggi badan siswa dalam kelas tertentu berada di atas 170 cm. Nah, konsep ini juga bisa dikaitkan dengan materi lain, seperti contoh soal bulughul maram contoh soal bulughul maram yang membahas tentang usia baligh.
Dalam soal bulughul maram, kita bisa menggunakan distribusi normal untuk menghitung probabilitas seseorang mencapai baligh pada usia tertentu. Kembali ke soal distribusi normal, dalam penyelesaiannya, kita biasanya menggunakan tabel distribusi normal standar atau kalkulator statistik untuk mendapatkan hasil yang akurat.
Bayangkan sebuah grafik dengan bentuk lonceng yang simetris. Pada puncak lonceng, terdapat nilai yang paling sering muncul, sementara semakin menjauh dari puncak, semakin jarang nilai tersebut muncul. Distribusi normal ini memiliki sifat unik yang membuatnya sangat berguna dalam menganalisis data.
Karakteristik Distribusi Normal
Berikut adalah beberapa karakteristik utama distribusi normal:
- Simetris: Kurva distribusi normal simetris terhadap mean, sehingga separuh data berada di sisi kiri mean dan separuh lainnya di sisi kanan.
- Bentuk Lonceng: Kurva distribusi normal berbentuk lonceng, dengan puncak yang mewakili mean, median, dan modus.
- Variasi: Distribusi normal memiliki variasi yang dapat diukur dengan standar deviasi. Standar deviasi menunjukkan seberapa tersebar data dari mean.
Contoh Penerapan Distribusi Normal
Distribusi normal banyak diterapkan dalam berbagai bidang, seperti:
- Ilmu Pengetahuan: Mengukur tinggi badan, berat badan, dan tekanan darah manusia.
- Teknik: Mengontrol kualitas produk manufaktur dan mengukur tingkat keandalan sistem.
- Sosial: Menganalisis pendapatan, skor ujian, dan preferensi konsumen.
Perbandingan dengan Distribusi Lainnya
Berikut adalah tabel perbandingan antara distribusi normal dengan distribusi Poisson dan distribusi binomial:
| Karakteristik | Distribusi Normal | Distribusi Poisson | Distribusi Binomial |
|---|---|---|---|
| Jenis Data | Data kontinu | Data diskrit | Data diskrit |
| Parameter | Mean (μ) dan Standar Deviasi (σ) | Rata-rata (λ) | Probabilitas keberhasilan (p) dan jumlah percobaan (n) |
| Bentuk | Kurva lonceng simetris | Kurva asimetris | Kurva asimetris |
| Contoh | Tinggi badan, berat badan | Jumlah panggilan telepon dalam satu jam | Jumlah sisi kepala saat melempar koin 10 kali |
Sifat Distribusi Normal
Distribusi normal adalah salah satu konsep penting dalam statistika, yang menggambarkan pola distribusi data yang sering muncul di berbagai bidang seperti ilmu sosial, ilmu alam, dan rekayasa. Distribusi normal memiliki beberapa sifat unik yang membuatnya mudah dikenali dan dipahami.
Bentuk Lonceng
Distribusi normal dikenal dengan bentuknya yang menyerupai lonceng. Dalam kurva distribusi normal, titik puncak mewakili nilai rata-rata (mean) dari data. Semakin jauh dari titik puncak, semakin sedikit frekuensi data yang muncul. Bentuk lonceng ini menunjukkan bahwa sebagian besar data berkumpul di sekitar nilai rata-rata, sementara data yang jauh dari rata-rata semakin jarang.
Simetris
Kurva distribusi normal bersifat simetris, artinya bagian kiri dan kanan kurva identik. Jika Anda membagi kurva menjadi dua bagian yang sama di titik puncak, kedua bagian tersebut akan menjadi cerminan satu sama lain. Sifat simetris ini menunjukkan bahwa data terdistribusi secara merata di sekitar nilai rata-rata.
Mean, Median, dan Modus yang Sama
Dalam distribusi normal, nilai rata-rata (mean), median, dan modus sama. Mean adalah nilai rata-rata dari semua data, median adalah nilai tengah dari data yang telah diurutkan, dan modus adalah nilai yang paling sering muncul dalam data. Ketiga nilai ini berhimpun di titik puncak kurva distribusi normal.
Contoh Data
Contoh data yang mengikuti distribusi normal adalah tinggi badan manusia. Tinggi badan manusia cenderung terdistribusi secara normal, dengan sebagian besar orang memiliki tinggi badan yang mendekati nilai rata-rata, sementara orang dengan tinggi badan yang sangat pendek atau sangat tinggi relatif sedikit. Data tinggi badan manusia memenuhi ketiga sifat distribusi normal:
- Bentuk Lonceng: Jika Anda membuat histogram dari data tinggi badan manusia, Anda akan melihat bahwa histogram tersebut berbentuk lonceng, dengan sebagian besar data berkumpul di sekitar nilai rata-rata.
- Simetris: Jika Anda membagi histogram tinggi badan menjadi dua bagian yang sama, Anda akan melihat bahwa kedua bagian tersebut simetris.
- Mean, Median, dan Modus yang Sama: Nilai rata-rata, median, dan modus dari data tinggi badan manusia akan berada di sekitar titik puncak histogram.
Parameter Distribusi Normal: Contoh Soal Distribusi Normal Dan Penyelesaiannya
Distribusi normal merupakan salah satu distribusi probabilitas yang paling sering digunakan dalam statistika. Bentuk kurva distribusi normal ditentukan oleh dua parameter utama, yaitu mean (μ) dan standar deviasi (σ). Kedua parameter ini memiliki peran penting dalam menentukan bentuk dan posisi kurva distribusi normal.
Mean (μ)
Mean (μ) merupakan nilai rata-rata dari data dalam distribusi normal. Mean menentukan pusat kurva distribusi normal. Jika nilai mean meningkat, kurva distribusi normal akan bergeser ke kanan. Sebaliknya, jika nilai mean menurun, kurva distribusi normal akan bergeser ke kiri.
Standar Deviasi (σ)
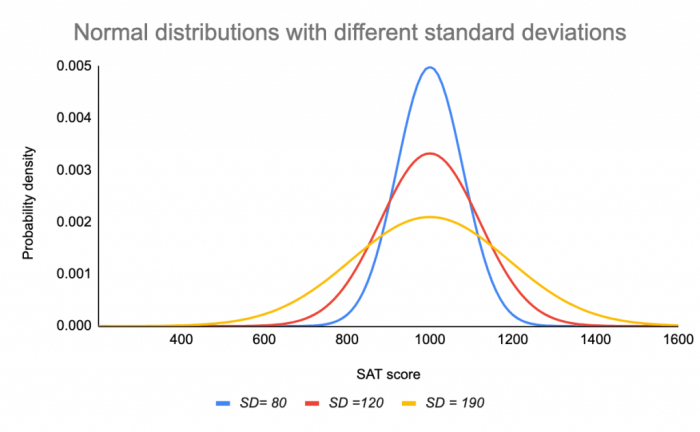
Standar deviasi (σ) mengukur penyebaran data di sekitar mean. Standar deviasi menentukan lebar atau kecuraman kurva distribusi normal. Semakin besar nilai standar deviasi, semakin lebar kurva distribusi normal. Sebaliknya, semakin kecil nilai standar deviasi, semakin sempit kurva distribusi normal.
Contoh Perubahan Nilai μ dan σ
- Jika nilai mean (μ) meningkat, kurva distribusi normal akan bergeser ke kanan. Misalnya, jika kita membandingkan distribusi tinggi badan pria dan wanita, distribusi tinggi badan pria cenderung memiliki mean yang lebih tinggi dibandingkan dengan distribusi tinggi badan wanita. Hal ini akan menyebabkan kurva distribusi tinggi badan pria bergeser ke kanan dibandingkan dengan kurva distribusi tinggi badan wanita.
- Jika nilai standar deviasi (σ) meningkat, kurva distribusi normal akan menjadi lebih lebar. Misalnya, jika kita membandingkan distribusi nilai ujian di dua kelas, kelas A memiliki standar deviasi yang lebih tinggi dibandingkan dengan kelas B. Hal ini akan menyebabkan kurva distribusi nilai ujian kelas A lebih lebar dibandingkan dengan kurva distribusi nilai ujian kelas B. Artinya, nilai ujian di kelas A lebih tersebar dibandingkan dengan nilai ujian di kelas B.
Menghitung Probabilitas, Contoh soal distribusi normal dan penyelesaiannya
Tabel distribusi normal standar digunakan untuk menghitung probabilitas berdasarkan nilai mean (μ) dan standar deviasi (σ). Tabel distribusi normal standar menunjukkan probabilitas untuk nilai z, yang merupakan nilai standar dari variabel acak. Nilai z dihitung dengan rumus:
z = (x – μ) / σ
Dimana:
- x adalah nilai variabel acak
- μ adalah mean
- σ adalah standar deviasi
Dengan menggunakan tabel distribusi normal standar, kita dapat mencari probabilitas untuk nilai z tertentu. Misalnya, jika kita ingin mencari probabilitas untuk nilai z kurang dari 1, kita dapat mencari nilai probabilitas yang sesuai dengan nilai z = 1 pada tabel distribusi normal standar. Probabilitas tersebut menunjukkan persentase data yang berada di bawah nilai z = 1.
Soal Distribusi Normal
Distribusi normal adalah salah satu distribusi probabilitas yang paling penting dalam statistika. Distribusi ini berbentuk seperti kurva lonceng, dengan sebagian besar data terpusat di sekitar nilai rata-rata. Distribusi normal banyak ditemukan di berbagai bidang, seperti ilmu sosial, ekonomi, dan kesehatan. Dalam artikel ini, kita akan membahas beberapa contoh soal distribusi normal dan penyelesaiannya.
Menghitung Probabilitas Suatu Nilai Berada dalam Rentang Tertentu
Salah satu aplikasi penting dari distribusi normal adalah untuk menghitung probabilitas suatu nilai berada dalam rentang tertentu. Misalnya, kita ingin mengetahui probabilitas tinggi badan siswa di suatu kelas berada di antara 160 cm dan 170 cm. Untuk menyelesaikan soal ini, kita perlu mengetahui rata-rata dan standar deviasi tinggi badan siswa tersebut.
- Misalkan rata-rata tinggi badan siswa adalah 165 cm dan standar deviasi adalah 5 cm.
- Kita dapat menggunakan tabel distribusi normal standar atau kalkulator online untuk menghitung probabilitas tersebut.
- Dengan menggunakan tabel atau kalkulator, kita dapat menemukan bahwa probabilitas tinggi badan siswa berada di antara 160 cm dan 170 cm adalah sekitar 68,27%.
Mencari Nilai Z-Score untuk Suatu Nilai Tertentu
Z-score adalah nilai yang menunjukkan berapa standar deviasi suatu nilai berada dari rata-rata. Z-score dapat digunakan untuk membandingkan nilai dari populasi yang berbeda, karena nilai z-score selalu memiliki rata-rata 0 dan standar deviasi 1.
- Misalkan kita ingin mengetahui nilai z-score untuk tinggi badan siswa yang berukuran 175 cm.
- Dengan menggunakan rumus z-score, yaitu z = (nilai – rata-rata) / standar deviasi, kita dapat menghitung z-score untuk tinggi badan 175 cm.
- Dalam kasus ini, z-score adalah (175 – 165) / 5 = 2. Ini berarti tinggi badan 175 cm berada 2 standar deviasi di atas rata-rata.
Mencari Nilai Data Berdasarkan Probabilitas yang Diberikan
Selain menghitung probabilitas, kita juga dapat menggunakan distribusi normal untuk mencari nilai data berdasarkan probabilitas yang diberikan. Misalnya, kita ingin mengetahui nilai tinggi badan siswa yang berada di persentil ke-90.
- Persentil ke-90 berarti bahwa 90% siswa memiliki tinggi badan di bawah nilai tersebut.
- Dengan menggunakan tabel distribusi normal standar atau kalkulator online, kita dapat menemukan nilai z-score yang sesuai dengan persentil ke-90.
- Nilai z-score untuk persentil ke-90 adalah sekitar 1,28.
- Dengan menggunakan rumus z-score, kita dapat mencari nilai tinggi badan siswa yang berada di persentil ke-90, yaitu 165 + (1,28 * 5) = 171,4 cm.
Penyelesaian Soal Distribusi Normal
Setelah memahami konsep distribusi normal dan sifat-sifatnya, kita dapat menerapkannya untuk menyelesaikan berbagai masalah. Dalam menyelesaikan soal distribusi normal, kita perlu mengidentifikasi variabel acak yang diukur, nilai mean dan standar deviasi, dan probabilitas yang ingin kita cari. Langkah-langkah umum dalam menyelesaikan soal distribusi normal adalah sebagai berikut:
Langkah-Langkah Umum dalam Menyelesaikan Soal Distribusi Normal
Langkah-langkah umum dalam menyelesaikan soal distribusi normal dapat diuraikan sebagai berikut:
- Tentukan variabel acak yang diukur dan pastikan bahwa variabel tersebut berdistribusi normal. Variabel acak merupakan variabel yang nilainya dapat berubah secara acak.
- Tentukan nilai mean (μ) dan standar deviasi (σ) dari distribusi normal. Mean merupakan nilai rata-rata dari variabel acak, sedangkan standar deviasi menunjukkan sebaran data dari mean.
- Tentukan probabilitas yang ingin dicari. Misalnya, kita ingin mencari probabilitas bahwa variabel acak berada di bawah atau di atas nilai tertentu, atau berada di antara dua nilai tertentu.
- Standarisasi variabel acak dengan menggunakan rumus:
Z = (X – μ) / σ
- Gunakan tabel distribusi normal standar atau kalkulator statistik untuk mencari probabilitas yang sesuai dengan nilai Z yang telah dihitung. Tabel distribusi normal standar menunjukkan probabilitas untuk berbagai nilai Z, sedangkan kalkulator statistik dapat digunakan untuk menghitung probabilitas secara langsung.
- Interpretasikan hasil yang diperoleh. Misalnya, jika kita mencari probabilitas bahwa variabel acak berada di bawah nilai tertentu, maka hasil yang diperoleh adalah probabilitas bahwa variabel acak akan mengambil nilai yang lebih kecil dari nilai tersebut.
Contoh Penyelesaian Soal Distribusi Normal dengan Tabel Distribusi Normal Standar
Misalnya, kita ingin mencari probabilitas bahwa tinggi badan siswa di suatu sekolah berada di bawah 170 cm. Diketahui bahwa tinggi badan siswa di sekolah tersebut berdistribusi normal dengan mean 175 cm dan standar deviasi 5 cm. Untuk menyelesaikan masalah ini, kita dapat menggunakan tabel distribusi normal standar sebagai berikut:
- Tentukan variabel acak yang diukur: Tinggi badan siswa (X)
- Tentukan nilai mean dan standar deviasi: μ = 175 cm, σ = 5 cm
- Tentukan probabilitas yang ingin dicari: P(X < 170 cm)
- Standarisasi variabel acak: Z = (170 – 175) / 5 = -1
- Gunakan tabel distribusi normal standar untuk mencari probabilitas yang sesuai dengan nilai Z = -1. Dari tabel distribusi normal standar, kita dapat menemukan bahwa P(Z < -1) = 0.1587.
- Interpretasikan hasil: Probabilitas bahwa tinggi badan siswa berada di bawah 170 cm adalah 0.1587 atau 15.87%.
Contoh Penyelesaian Soal Distribusi Normal dengan Kalkulator atau Software Statistik
Misalnya, kita ingin mencari probabilitas bahwa berat badan bayi baru lahir berada di antara 3 kg dan 4 kg. Diketahui bahwa berat badan bayi baru lahir berdistribusi normal dengan mean 3.5 kg dan standar deviasi 0.5 kg. Untuk menyelesaikan masalah ini, kita dapat menggunakan kalkulator statistik atau software statistik seperti SPSS atau R sebagai berikut:
- Tentukan variabel acak yang diukur: Berat badan bayi baru lahir (X)
- Tentukan nilai mean dan standar deviasi: μ = 3.5 kg, σ = 0.5 kg
- Tentukan probabilitas yang ingin dicari: P(3 kg < X < 4 kg)
- Gunakan fungsi distribusi normal pada kalkulator statistik atau software statistik untuk menghitung probabilitas yang sesuai. Misalnya, pada kalkulator statistik, kita dapat menggunakan fungsi “normalcdf” dengan parameter 3, 4, 3.5, dan 0.5 untuk menghitung probabilitas tersebut.
- Interpretasikan hasil: Hasil yang diperoleh adalah probabilitas bahwa berat badan bayi baru lahir berada di antara 3 kg dan 4 kg.
Penerapan Distribusi Normal
Distribusi normal, juga dikenal sebagai kurva lonceng, merupakan salah satu konsep paling penting dalam statistika dan memiliki aplikasi luas di berbagai bidang, termasuk ilmu pengetahuan, teknik, dan kehidupan sehari-hari. Distribusi normal menggambarkan bagaimana data cenderung tersebar di sekitar nilai rata-rata, dengan sebagian besar data berkumpul di sekitar nilai rata-rata dan semakin sedikit data yang terdapat di ujung-ujung distribusi.
Penerapan dalam Statistik, Ilmu Pengetahuan, dan Teknik
Distribusi normal memiliki peran penting dalam berbagai bidang karena kemampuannya untuk memodelkan berbagai fenomena secara akurat. Dalam statistika, distribusi normal digunakan untuk melakukan pengujian hipotesis, membangun interval kepercayaan, dan melakukan analisis regresi. Dalam ilmu pengetahuan, distribusi normal digunakan untuk memodelkan data eksperimen, seperti tinggi badan, berat badan, dan tekanan darah. Dalam teknik, distribusi normal digunakan untuk mengontrol kualitas, merancang proses, dan menganalisis data kegagalan.
Contoh Penerapan Distribusi Normal
Kesehatan
Distribusi normal digunakan dalam berbagai bidang kesehatan, seperti dalam studi epidemiologi, penelitian klinis, dan pemantauan kesehatan. Misalnya, distribusi normal dapat digunakan untuk memodelkan tekanan darah, kadar kolesterol, dan tinggi badan pada populasi. Informasi ini kemudian dapat digunakan untuk mengidentifikasi orang-orang yang berisiko terkena penyakit tertentu atau untuk memantau efektivitas pengobatan.
Ekonomi
Dalam ekonomi, distribusi normal digunakan untuk memodelkan berbagai variabel ekonomi, seperti pendapatan, harga saham, dan tingkat inflasi. Misalnya, distribusi normal dapat digunakan untuk memodelkan distribusi pendapatan dalam suatu negara. Informasi ini kemudian dapat digunakan untuk menganalisis ketidaksetaraan pendapatan dan merumuskan kebijakan ekonomi yang tepat.
Sosial
Distribusi normal juga memiliki aplikasi dalam bidang sosial, seperti dalam studi demografi, sosiologi, dan psikologi. Misalnya, distribusi normal dapat digunakan untuk memodelkan distribusi usia, tingkat pendidikan, dan kepuasan hidup dalam suatu populasi. Informasi ini kemudian dapat digunakan untuk memahami tren sosial, merumuskan kebijakan sosial, dan mengembangkan program intervensi.
Peran Distribusi Normal dalam Pengambilan Keputusan dan Analisis Data
Distribusi normal merupakan alat yang sangat berharga dalam pengambilan keputusan dan analisis data. Dengan memahami distribusi normal, kita dapat mengidentifikasi pola dalam data, menguji hipotesis, dan membuat prediksi yang akurat. Misalnya, dalam penelitian klinis, distribusi normal dapat digunakan untuk menentukan apakah pengobatan baru efektif dalam mengurangi gejala penyakit. Dalam bisnis, distribusi normal dapat digunakan untuk memprediksi permintaan produk, mengelola inventaris, dan membuat keputusan tentang penetapan harga.
Contoh Soal dan Penyelesaian
Distribusi normal adalah salah satu konsep penting dalam statistika. Dalam kehidupan sehari-hari, banyak data yang mengikuti distribusi normal, seperti tinggi badan, berat badan, dan skor ujian. Memahami distribusi normal memungkinkan kita untuk menganalisis data dan membuat prediksi yang akurat.
Untuk memahami distribusi normal lebih lanjut, mari kita lihat beberapa contoh soal dan penyelesaiannya.
Contoh Soal dan Penyelesaian Distribusi Normal
Berikut adalah beberapa contoh soal distribusi normal dan penyelesaiannya yang mencakup berbagai jenis soal, seperti menghitung probabilitas, mencari nilai z-score, dan mencari nilai data:
| No. | Soal | Penyelesaian |
|---|---|---|
| 1 | Misalkan tinggi badan mahasiswa di suatu universitas berdistribusi normal dengan rata-rata 170 cm dan standar deviasi 5 cm. Berapa probabilitas seorang mahasiswa memiliki tinggi badan di atas 175 cm? |
|
| 2 | Skor ujian matematika di suatu kelas berdistribusi normal dengan rata-rata 70 dan standar deviasi 10. Berapa skor yang dibutuhkan untuk berada di 90% teratas? |
|
| 3 | Berat badan bayi baru lahir di suatu rumah sakit berdistribusi normal dengan rata-rata 3,5 kg dan standar deviasi 0,5 kg. Berapa probabilitas bayi baru lahir memiliki berat badan antara 3 kg dan 4 kg? |
|
| 4 | Misalkan skor TOEFL berdistribusi normal dengan rata-rata 500 dan standar deviasi 100. Jika seorang mahasiswa memperoleh skor 650, berapa persentil skornya? |
|
| 5 | Suatu perusahaan memproduksi bohlam lampu dengan umur rata-rata 1000 jam dan standar deviasi 100 jam. Jika umur bohlam lampu berdistribusi normal, berapa persen bohlam lampu yang memiliki umur lebih dari 1150 jam? |
|
Distribusi Normal Standar
Distribusi normal standar merupakan bentuk khusus dari distribusi normal dengan rata-rata (mean) 0 dan deviasi standar 1. Distribusi normal standar sangat penting dalam statistika karena memungkinkan kita untuk menghitung probabilitas untuk berbagai nilai dalam distribusi normal. Dengan kata lain, distribusi normal standar adalah versi “standar” dari distribusi normal, yang memudahkan kita untuk membandingkan data dari distribusi normal yang berbeda.
Hubungan Distribusi Normal Standar dengan Distribusi Normal
Setiap distribusi normal dapat diubah menjadi distribusi normal standar dengan menggunakan transformasi Z. Transformasi Z adalah proses mengubah nilai variabel acak dari distribusi normal menjadi nilai setara dalam distribusi normal standar. Formula transformasi Z adalah:
Z = (X – μ) / σ
Dimana:
- Z adalah skor Z, yang merupakan nilai variabel acak dalam distribusi normal standar.
- X adalah nilai variabel acak dalam distribusi normal asli.
- μ adalah rata-rata (mean) distribusi normal asli.
- σ adalah deviasi standar distribusi normal asli.
Contoh Mengubah Distribusi Normal ke Distribusi Normal Standar
Misalnya, jika kita memiliki distribusi normal dengan rata-rata 10 dan deviasi standar 2, dan kita ingin mencari probabilitas bahwa nilai variabel acak berada di bawah 12. Kita dapat mengubah nilai 12 menjadi skor Z dengan menggunakan formula transformasi Z:
Z = (12 – 10) / 2 = 1
Ini berarti bahwa nilai 12 dalam distribusi normal asli setara dengan skor Z 1 dalam distribusi normal standar. Kita kemudian dapat menggunakan tabel distribusi normal standar untuk mencari probabilitas bahwa skor Z berada di bawah 1.
Menggunakan Tabel Distribusi Normal Standar untuk Mencari Probabilitas
Tabel distribusi normal standar menunjukkan probabilitas untuk berbagai nilai skor Z. Tabel ini menunjukkan area di bawah kurva distribusi normal standar, yang mewakili probabilitas bahwa variabel acak akan berada di bawah skor Z tertentu.
Untuk menggunakan tabel distribusi normal standar, kita perlu mencari skor Z yang sesuai dengan nilai variabel acak yang ingin kita cari probabilitasnya. Setelah menemukan skor Z, kita dapat melihat nilai probabilitas yang sesuai di tabel. Misalnya, jika kita ingin mencari probabilitas bahwa skor Z berada di bawah 1, kita akan menemukan nilai 1 di kolom pertama tabel dan nilai 0 di kolom kedua tabel. Nilai probabilitas yang sesuai adalah 0.8413, yang berarti bahwa probabilitas bahwa skor Z berada di bawah 1 adalah 84.13%.
Aplikasi Distribusi Normal
Distribusi normal, juga dikenal sebagai kurva lonceng, adalah salah satu distribusi probabilitas yang paling umum digunakan dalam statistik. Distribusi ini memodelkan banyak fenomena alam dan buatan manusia, seperti tinggi badan manusia, tekanan darah, skor tes, dan bahkan nilai saham.
Kontrol Kualitas
Distribusi normal digunakan dalam kontrol kualitas untuk menetapkan batas toleransi untuk produk atau proses. Batas toleransi ini menentukan rentang nilai yang dapat diterima untuk suatu karakteristik produk atau proses.
- Misalnya, dalam manufaktur suku cadang mobil, distribusi normal dapat digunakan untuk menentukan batas toleransi untuk diameter baut. Jika diameter baut berada di luar batas toleransi, baut tersebut dianggap cacat dan harus dibuang.
Pengujian Hipotesis
Distribusi normal digunakan dalam pengujian hipotesis untuk menguji signifikansi perbedaan antara dua kelompok data.
- Misalnya, sebuah perusahaan farmasi mungkin ingin menguji apakah obat baru lebih efektif daripada obat lama dalam mengobati suatu penyakit. Mereka dapat menggunakan distribusi normal untuk menguji signifikansi perbedaan antara kelompok yang menerima obat baru dan kelompok yang menerima obat lama.
Prediksi
Distribusi normal dapat digunakan untuk membuat prediksi tentang nilai variabel di masa depan.
- Misalnya, sebuah perusahaan asuransi dapat menggunakan distribusi normal untuk memprediksi jumlah klaim yang akan mereka terima dalam periode waktu tertentu. Mereka dapat menggunakan data historis tentang klaim untuk membangun model distribusi normal dan menggunakannya untuk memprediksi klaim di masa depan.
Aplikasi di Berbagai Bidang
Distribusi normal memiliki aplikasi yang luas di berbagai bidang, termasuk:
- Ilmu Komputer: Distribusi normal digunakan dalam pemrosesan sinyal, pengenalan pola, dan pembelajaran mesin.
- Keuangan: Distribusi normal digunakan dalam pemodelan portofolio, manajemen risiko, dan penilaian aset.
- Ilmu Sosial: Distribusi normal digunakan dalam penelitian sosial, seperti studi tentang kepuasan pelanggan, perilaku konsumen, dan pendapat publik.
Penutupan
Memahami distribusi normal adalah kunci untuk memahami pola data di sekitar kita. Dari tinggi badan manusia hingga skor ujian, konsep ini membantu kita menganalisis data, membuat prediksi, dan memahami berbagai fenomena. Dengan mempelajari contoh soal distribusi normal dan penyelesaiannya, kita dapat memperoleh pemahaman yang lebih dalam tentang dunia data dan memanfaatkannya untuk membuat keputusan yang lebih baik dalam berbagai bidang.






