Contoh soal distribusi normal dan penyelesaiannya pdf – Pernahkah Anda bertanya-tanya bagaimana data seperti tinggi badan, berat badan, atau skor ujian tersebar dalam suatu populasi? Distribusi normal, sebuah konsep penting dalam statistik, membantu kita memahami pola penyebaran data tersebut. Dalam artikel ini, kita akan menjelajahi contoh soal distribusi normal dan penyelesaiannya yang disajikan dalam format PDF, sehingga Anda dapat mempelajari dan mempraktikkan konsep ini dengan mudah.
Distribusi normal merupakan model matematika yang menggambarkan bagaimana data terdistribusi secara simetris di sekitar rata-rata. Kurva berbentuk lonceng yang khas dari distribusi normal menunjukkan bahwa sebagian besar data berkumpul di sekitar rata-rata, sementara semakin jauh dari rata-rata, semakin sedikit data yang ditemukan.
Pengertian Distribusi Normal
Distribusi normal adalah salah satu konsep penting dalam statistika yang menggambarkan pola distribusi data yang sering muncul dalam berbagai bidang, mulai dari ilmu sosial hingga ilmu alam. Dalam distribusi normal, data cenderung terpusat di sekitar nilai tengah (rata-rata) dan semakin menjauh dari nilai tengah, frekuensi kemunculan data semakin rendah.
Mempelajari contoh soal distribusi normal dan penyelesaiannya pdf memang penting, terutama jika kamu ingin memahami konsep probabilitas dan statistika dengan lebih baik. Nah, untuk mengasah kemampuanmu dalam memahami dan mengaplikasikan konsep tersebut, kamu juga bisa mencoba mengerjakan contoh soal interview accounting terbaru yang bisa kamu temukan di situs ini.
Soal-soal tersebut akan membantumu untuk menguji pemahamanmu tentang konsep akuntansi yang berkaitan dengan statistika, seperti analisis data keuangan dan perencanaan keuangan.
Contoh Penerapan Distribusi Normal dalam Kehidupan Nyata
Distribusi normal dapat ditemukan dalam berbagai aspek kehidupan, contohnya:
- Tinggi badan manusia: Jika kita mengukur tinggi badan dari banyak orang, maka data yang diperoleh akan cenderung terdistribusi normal, dengan sebagian besar orang memiliki tinggi badan yang mendekati nilai rata-rata dan semakin sedikit orang yang memiliki tinggi badan yang sangat pendek atau sangat tinggi.
- Skor ujian: Hasil ujian dari suatu kelas biasanya terdistribusi normal, dengan sebagian besar siswa mendapatkan skor yang mendekati nilai rata-rata, dan semakin sedikit siswa yang mendapatkan skor yang sangat rendah atau sangat tinggi.
- Tekanan darah: Tekanan darah manusia juga terdistribusi normal, dengan sebagian besar orang memiliki tekanan darah yang normal, dan semakin sedikit orang yang memiliki tekanan darah yang sangat rendah atau sangat tinggi.
Ciri-Ciri Distribusi Normal
Distribusi normal memiliki beberapa ciri khas, antara lain:
- Bentuknya simetris: Kurva distribusi normal berbentuk lonceng, simetris terhadap nilai rata-rata. Artinya, data di sebelah kiri rata-rata memiliki frekuensi yang sama dengan data di sebelah kanan rata-rata.
- Nilai rata-rata, median, dan modus sama: Pada distribusi normal, nilai rata-rata (mean), median, dan modus berada pada titik yang sama, yaitu puncak kurva.
- Area di bawah kurva sama dengan 1: Luas total di bawah kurva distribusi normal selalu sama dengan 1, yang menunjukkan bahwa semua data tercakup dalam kurva.
Ilustrasi Kurva Distribusi Normal
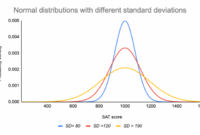
Kurva distribusi normal berbentuk lonceng, dengan puncak kurva berada di nilai rata-rata. Semakin jauh dari nilai rata-rata, frekuensi data semakin rendah. Berikut adalah ilustrasi kurva distribusi normal:
[Ilustrasi kurva distribusi normal dengan keterangan: sumbu x menunjukkan nilai data, sumbu y menunjukkan frekuensi, puncak kurva menunjukkan nilai rata-rata, dan area di bawah kurva menunjukkan persentase data pada setiap deviasi standar.]
Persentase Data pada Setiap Deviasi Standar
Deviasi standar adalah ukuran sebaran data dari nilai rata-rata. Pada distribusi normal, persentase data yang berada pada setiap deviasi standar dari rata-rata adalah sebagai berikut:
| Deviasi Standar | Persentase Data |
|---|---|
| ±1 deviasi standar | 68.27% |
| ±2 deviasi standar | 95.45% |
| ±3 deviasi standar | 99.73% |
Soal Distribusi Normal: Contoh Soal Distribusi Normal Dan Penyelesaiannya Pdf
Distribusi normal merupakan salah satu distribusi probabilitas yang paling penting dalam statistika. Distribusi ini sering digunakan untuk memodelkan data yang berdistribusi secara simetris, seperti tinggi badan, berat badan, dan nilai ujian. Dalam distribusi normal, data cenderung terpusat di sekitar nilai rata-rata, dengan probabilitas yang lebih rendah untuk nilai yang jauh dari rata-rata.
Untuk menyelesaikan soal distribusi normal, kita perlu menggunakan tabel distribusi normal standar atau kalkulator statistik. Tabel distribusi normal standar memberikan probabilitas untuk berbagai nilai z-score, yang merupakan ukuran jarak antara nilai data dan rata-rata dalam satuan deviasi standar.
Contoh Soal Distribusi Normal yang Melibatkan Perhitungan Probabilitas
Misalnya, kita ingin mengetahui probabilitas bahwa nilai ujian mahasiswa dalam suatu mata kuliah tertentu akan berada di atas 80, jika diketahui bahwa nilai ujian tersebut berdistribusi normal dengan rata-rata 75 dan deviasi standar 5. Untuk menyelesaikan soal ini, kita perlu menghitung z-score untuk nilai 80, kemudian menggunakan tabel distribusi normal standar untuk mencari probabilitas yang sesuai.
- Z-score untuk nilai 80 adalah (80 – 75) / 5 = 1.
- Dari tabel distribusi normal standar, kita dapat menemukan bahwa probabilitas untuk z-score lebih besar dari 1 adalah 0,1587.
- Jadi, probabilitas bahwa nilai ujian mahasiswa akan berada di atas 80 adalah 0,1587 atau 15,87%.
Contoh Soal Distribusi Normal yang Melibatkan Penentuan Nilai Z-score
Misalnya, kita ingin mengetahui nilai z-score yang sesuai dengan probabilitas 0,95 dalam distribusi normal standar. Untuk menyelesaikan soal ini, kita perlu menggunakan tabel distribusi normal standar atau kalkulator statistik untuk mencari nilai z-score yang sesuai dengan probabilitas 0,95.
- Dari tabel distribusi normal standar, kita dapat menemukan bahwa nilai z-score yang sesuai dengan probabilitas 0,95 adalah 1,645.
- Ini berarti bahwa 95% dari data dalam distribusi normal standar berada di bawah nilai z-score 1,645.
Contoh Soal Distribusi Normal yang Melibatkan Penentuan Nilai Kritis
Misalnya, kita ingin menentukan nilai kritis untuk uji hipotesis satu sisi kanan dengan tingkat signifikansi 0,05 dalam distribusi normal standar. Untuk menyelesaikan soal ini, kita perlu menggunakan tabel distribusi normal standar atau kalkulator statistik untuk mencari nilai z-score yang sesuai dengan probabilitas 0,05.
- Dari tabel distribusi normal standar, kita dapat menemukan bahwa nilai z-score yang sesuai dengan probabilitas 0,05 adalah 1,645.
- Jadi, nilai kritis untuk uji hipotesis satu sisi kanan dengan tingkat signifikansi 0,05 adalah 1,645.
- Jika nilai statistik uji lebih besar dari 1,645, maka kita menolak hipotesis nol.
Aplikasi Distribusi Normal
Distribusi normal, juga dikenal sebagai kurva lonceng, merupakan salah satu konsep penting dalam statistika dan ilmu probabilitas. Distribusi ini memiliki banyak aplikasi di berbagai bidang, termasuk statistika, ekonomi, dan kesehatan.
Aplikasi Distribusi Normal dalam Berbagai Bidang
Distribusi normal memiliki peran penting dalam berbagai bidang karena kemampuannya dalam memodelkan data yang terdistribusi secara simetris.
- Statistika: Distribusi normal digunakan untuk menguji hipotesis, membangun interval kepercayaan, dan menganalisis data. Banyak uji statistik, seperti uji t dan uji z, mengasumsikan bahwa data terdistribusi normal.
- Ekonomi: Distribusi normal digunakan untuk memodelkan variabel ekonomi seperti pendapatan, harga, dan tingkat inflasi. Dalam analisis keuangan, distribusi normal digunakan untuk menilai risiko investasi dan memodelkan pengembalian portofolio.
- Kesehatan: Distribusi normal digunakan untuk memodelkan variabel kesehatan seperti tekanan darah, tinggi badan, dan berat badan. Dalam penelitian medis, distribusi normal digunakan untuk menganalisis data klinis dan menguji efektivitas pengobatan.
Penjelasan Probabilitas pada Distribusi Normal

Distribusi normal adalah salah satu distribusi probabilitas yang paling penting dalam statistika. Distribusi ini sering digunakan untuk memodelkan data yang terdistribusi secara simetris, dengan banyak data terkonsentrasi di sekitar rata-rata. Distribusi normal memiliki sifat unik yang memungkinkan kita untuk menghitung probabilitas kejadian tertentu.
Konsep Probabilitas pada Distribusi Normal
Probabilitas pada distribusi normal mengacu pada kemungkinan suatu nilai acak yang diambil dari distribusi normal akan jatuh dalam rentang tertentu. Karena distribusi normal adalah distribusi kontinu, probabilitas dihitung sebagai luas di bawah kurva distribusi normal. Luas ini mewakili proporsi dari semua nilai yang mungkin yang jatuh dalam rentang tertentu.
Menentukan Probabilitas pada Distribusi Normal
Untuk menentukan probabilitas suatu kejadian pada distribusi normal, kita perlu mengetahui mean (μ) dan standar deviasi (σ) dari distribusi tersebut. Kemudian, kita dapat menggunakan tabel distribusi normal standar atau perangkat lunak statistika untuk menghitung probabilitas.
Misalnya, jika kita ingin mengetahui probabilitas bahwa nilai acak yang diambil dari distribusi normal dengan mean 100 dan standar deviasi 10 akan jatuh antara 90 dan 110, kita dapat menggunakan tabel distribusi normal standar atau perangkat lunak statistika untuk menghitung probabilitas.
Interpretasi Probabilitas
Probabilitas yang diperoleh dari distribusi normal dapat diinterpretasikan sebagai proporsi dari semua nilai yang mungkin yang jatuh dalam rentang tertentu. Misalnya, jika probabilitas bahwa nilai acak jatuh antara 90 dan 110 adalah 0.68, maka 68% dari semua nilai yang mungkin akan jatuh dalam rentang tersebut.
Probabilitas ini dapat digunakan untuk membuat keputusan berdasarkan data. Misalnya, jika kita tahu bahwa nilai acak memiliki probabilitas tinggi jatuh dalam rentang tertentu, kita dapat menganggap bahwa nilai tersebut berada dalam rentang tersebut.
Contoh Ilustrasi, Contoh soal distribusi normal dan penyelesaiannya pdf
Misalnya, kita ingin mengetahui probabilitas bahwa tinggi badan seorang pria dewasa akan berada antara 170 cm dan 180 cm. Asumsikan bahwa tinggi badan pria dewasa terdistribusi normal dengan mean 175 cm dan standar deviasi 5 cm.
Kita dapat menggunakan tabel distribusi normal standar atau perangkat lunak statistika untuk menghitung probabilitas. Hasilnya menunjukkan bahwa probabilitas bahwa tinggi badan pria dewasa akan berada antara 170 cm dan 180 cm adalah sekitar 0.68. Ini berarti bahwa sekitar 68% dari semua pria dewasa memiliki tinggi badan antara 170 cm dan 180 cm.
Kesimpulan
Distribusi normal adalah alat yang sangat berguna untuk memodelkan data yang terdistribusi secara simetris. Probabilitas pada distribusi normal dapat digunakan untuk membuat keputusan berdasarkan data dan memahami probabilitas suatu kejadian tertentu.
Penggunaan Tabel Distribusi Normal Standar
Tabel distribusi normal standar adalah alat yang sangat berguna untuk menghitung probabilitas dalam distribusi normal. Tabel ini menampilkan luas di bawah kurva distribusi normal standar untuk berbagai nilai z-score. Memahami cara membaca tabel ini dan menggunakannya untuk menghitung probabilitas dan nilai z-score sangat penting dalam analisis statistik.
Cara Membaca Tabel Distribusi Normal Standar
Tabel distribusi normal standar biasanya disusun dalam dua bagian. Bagian pertama menampilkan nilai z-score di kolom pertama dan baris pertama tabel. Bagian kedua menampilkan luas di bawah kurva distribusi normal standar yang sesuai dengan nilai z-score tersebut. Untuk membaca tabel, Anda perlu menemukan nilai z-score yang ingin Anda cari di kolom pertama dan baris pertama tabel. Kemudian, cari persimpangan dari kolom dan baris tersebut untuk menemukan luas di bawah kurva yang sesuai dengan nilai z-score tersebut.
Cara Menggunakan Tabel Distribusi Normal Standar untuk Menentukan Probabilitas
Tabel distribusi normal standar dapat digunakan untuk menentukan probabilitas bahwa suatu nilai acak akan jatuh di antara dua nilai tertentu. Misalnya, untuk menentukan probabilitas bahwa nilai acak akan jatuh di antara z-score 0 dan 1, Anda perlu menemukan luas di bawah kurva yang sesuai dengan z-score 1. Luas ini mewakili probabilitas bahwa nilai acak akan jatuh di antara 0 dan 1.
Cara Menggunakan Tabel Distribusi Normal Standar untuk Menentukan Nilai Z-Score
Tabel distribusi normal standar juga dapat digunakan untuk menentukan nilai z-score yang sesuai dengan probabilitas tertentu. Misalnya, untuk menentukan nilai z-score yang sesuai dengan probabilitas 0,95, Anda perlu menemukan luas di bawah kurva yang paling dekat dengan 0,95. Kemudian, cari nilai z-score yang sesuai dengan luas tersebut.
Pentingnya Distribusi Normal
Distribusi normal merupakan salah satu konsep fundamental dalam statistika. Keberadaannya yang mendominasi dalam berbagai fenomena alam dan sosial membuat distribusi normal menjadi alat yang sangat penting dalam analisis data dan pengambilan keputusan.
Penggunaan Distribusi Normal dalam Statistik
Distribusi normal memegang peran penting dalam statistik karena kemampuannya untuk menggambarkan berbagai macam data yang muncul secara alami. Banyak variabel, seperti tinggi badan, berat badan, tekanan darah, dan skor ujian, cenderung mengikuti distribusi normal. Dengan menggunakan distribusi normal, kita dapat:
- Menentukan probabilitas suatu nilai variabel tertentu akan terjadi.
- Membandingkan data dari berbagai kelompok.
- Membuat estimasi dan prediksi.
Penggunaan Distribusi Normal dalam Pengambilan Keputusan
Dalam pengambilan keputusan, distribusi normal digunakan untuk menganalisis data dan membuat keputusan yang tepat. Misalnya, dalam industri manufaktur, distribusi normal dapat digunakan untuk mengontrol kualitas produk. Dengan memahami distribusi normal dari ukuran produk, produsen dapat menentukan batas toleransi yang dapat diterima dan meminimalkan produksi produk yang cacat.
Penggunaan Distribusi Normal dalam Penelitian Ilmiah
Distribusi normal juga merupakan alat penting dalam penelitian ilmiah. Banyak penelitian menggunakan distribusi normal untuk menganalisis data dan menguji hipotesis. Misalnya, dalam penelitian klinis, distribusi normal digunakan untuk membandingkan efektivitas dua jenis obat. Dengan menggunakan distribusi normal, peneliti dapat menentukan apakah perbedaan efektivitas antara dua obat signifikan secara statistik.
Ringkasan Akhir
Memahami distribusi normal sangat penting dalam berbagai bidang, mulai dari penelitian ilmiah hingga pengambilan keputusan bisnis. Dengan mempelajari contoh soal dan penyelesaiannya, Anda dapat menguasai konsep ini dan menerapkannya dalam berbagai situasi.