Contoh soal ketaksamaan – Pernahkah kamu merasa penasaran dengan konsep “lebih besar dari” atau “kurang dari” dalam matematika? Nah, konsep inilah yang menjadi dasar dari ketaksamaan. Ketaksamaan merupakan bagian penting dalam matematika yang membantu kita untuk menyelesaikan berbagai masalah yang melibatkan perbandingan nilai. Mulai dari menentukan batas kecepatan kendaraan hingga menganalisis pertumbuhan ekonomi, ketaksamaan memiliki peran yang luas dalam kehidupan kita.
Dalam artikel ini, kita akan menjelajahi dunia ketaksamaan dengan membahas pengertian, cara menyelesaikan, dan penerapannya dalam berbagai bidang. Selain itu, kita juga akan mempelajari berbagai jenis ketaksamaan dan sifat-sifatnya. Mari kita mulai petualangan kita memahami konsep ketaksamaan!
Pengertian Ketaksamaan
Ketaksamaan dalam matematika merupakan suatu pernyataan yang menyatakan hubungan antara dua ekspresi matematika yang tidak sama. Ketaksamaan digunakan untuk menunjukkan bahwa satu ekspresi lebih besar, lebih kecil, lebih besar atau sama dengan, atau lebih kecil atau sama dengan ekspresi lainnya. Ketaksamaan memiliki peran penting dalam berbagai bidang matematika, seperti aljabar, kalkulus, dan geometri, serta dalam aplikasi praktis di bidang seperti ekonomi, fisika, dan teknik.
Jenis-jenis Ketaksamaan
Ketaksamaan dapat dibedakan berdasarkan jenis hubungan yang dinyatakannya. Berikut adalah beberapa jenis ketaksamaan yang umum:
- Ketaksamaan Linear: Ketaksamaan linear adalah ketaksamaan yang melibatkan variabel dengan pangkat tertinggi 1. Contoh: 2x + 3 > 5, 4 – y ≤ 10.
- Ketaksamaan Kuadrat: Ketaksamaan kuadrat adalah ketaksamaan yang melibatkan variabel dengan pangkat tertinggi 2. Contoh: x2 – 4x + 3 < 0, 2y2 + 5y – 3 ≥ 0.
- Ketaksamaan Absolut: Ketaksamaan absolut melibatkan nilai absolut dari ekspresi matematika. Contoh: |x – 2| < 3, |2y + 1| ≥ 5.
- Ketaksamaan Rasional: Ketaksamaan rasional melibatkan variabel dalam bentuk pecahan. Contoh: (x + 1) / (x – 2) > 0, (2y – 3) / (y + 1) ≤ 4.
Contoh Ketaksamaan
Berikut adalah beberapa contoh ketaksamaan dan interpretasinya:
| Jenis Ketaksamaan | Contoh | Interpretasi |
|---|---|---|
| Ketaksamaan Linear | 2x + 3 > 5 | Nilai x yang memenuhi ketaksamaan ini adalah semua nilai x yang lebih besar dari 1. |
| Ketaksamaan Kuadrat | x2 – 4x + 3 < 0 | Nilai x yang memenuhi ketaksamaan ini adalah semua nilai x yang berada di antara 1 dan 3. |
| Ketaksamaan Absolut | |x – 2| < 3 | Nilai x yang memenuhi ketaksamaan ini adalah semua nilai x yang berada di antara -1 dan 5. |
| Ketaksamaan Rasional | (x + 1) / (x – 2) > 0 | Nilai x yang memenuhi ketaksamaan ini adalah semua nilai x yang lebih kecil dari -1 atau lebih besar dari 2. |
Menyelesaikan Ketaksamaan: Contoh Soal Ketaksamaan
Ketaksamaan merupakan pernyataan matematis yang membandingkan dua ekspresi dengan menggunakan tanda “<", ">“, “≤”, atau “≥”. Ketaksamaan linear dan kuadrat merupakan jenis ketaksamaan yang umum dipelajari dalam matematika. Pada bagian ini, kita akan membahas cara menyelesaikan kedua jenis ketaksamaan ini.
Menyelesaikan Ketaksamaan Linear
Ketaksamaan linear adalah ketaksamaan yang melibatkan variabel dengan pangkat tertinggi 1. Untuk menyelesaikan ketaksamaan linear, kita dapat menggunakan langkah-langkah berikut:
- Sederhanakan kedua sisi ketaksamaan dengan menggabungkan suku-suku sejenis.
- Tambahkan atau kurangi bilangan yang sama pada kedua sisi ketaksamaan.
- Kalikan atau bagi kedua sisi ketaksamaan dengan bilangan yang sama. Perhatikan bahwa jika kita mengalikan atau membagi dengan bilangan negatif, tanda ketaksamaan harus dibalik.
- Tuliskan solusi dalam bentuk interval.
Contohnya, perhatikan ketaksamaan berikut:
2x + 3 < 7
Untuk menyelesaikan ketaksamaan ini, kita dapat melakukan langkah-langkah berikut:
- Kurangi 3 dari kedua sisi: 2x < 4
- Bagi kedua sisi dengan 2: x < 2
Solusi dari ketaksamaan ini adalah x < 2, yang dapat ditulis dalam bentuk interval sebagai (-∞, 2).
Menyelesaikan Ketaksamaan Kuadrat
Ketaksamaan kuadrat adalah ketaksamaan yang melibatkan variabel dengan pangkat tertinggi 2. Untuk menyelesaikan ketaksamaan kuadrat, kita dapat menggunakan langkah-langkah berikut:
- Pindahkan semua suku ke satu sisi ketaksamaan sehingga sisi kanan sama dengan 0.
- Faktorkan ekspresi kuadrat di sisi kiri.
- Tentukan nilai-nilai x yang membuat ekspresi kuadrat sama dengan 0.
- Buat tabel tanda untuk menentukan interval-interval di mana ekspresi kuadrat bernilai positif atau negatif.
- Tuliskan solusi dalam bentuk interval.
Contohnya, perhatikan ketaksamaan berikut:
x² – 4x + 3 > 0
Untuk menyelesaikan ketaksamaan ini, kita dapat melakukan langkah-langkah berikut:
- Faktorkan ekspresi kuadrat: (x – 1)(x – 3) > 0
- Tentukan nilai-nilai x yang membuat ekspresi kuadrat sama dengan 0: x = 1 atau x = 3.
- Buat tabel tanda:
- Solusi dari ketaksamaan ini adalah x < 1 atau x > 3, yang dapat ditulis dalam bentuk interval sebagai (-∞, 1) U (3, ∞).
| Interval | x – 1 | x – 3 | (x – 1)(x – 3) |
|---|---|---|---|
| x < 1 | – | – | + |
| 1 < x < 3 | + | – | – |
| x > 3 | + | + | + |
Menggambar Grafik Ketaksamaan
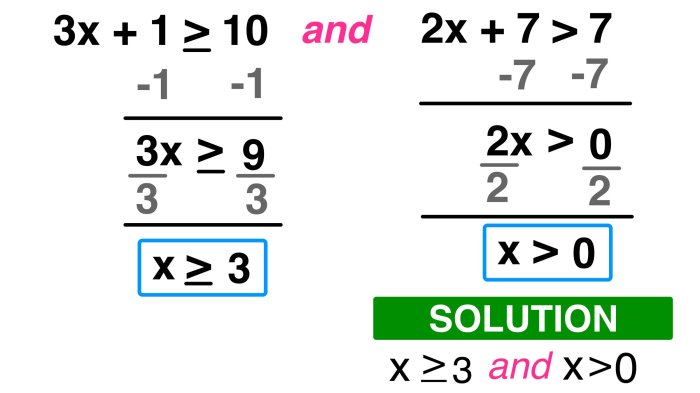
Menggambar grafik ketaksamaan adalah salah satu cara untuk memvisualisasikan solusi dari sebuah ketaksamaan. Grafik ketaksamaan menunjukkan daerah yang memuat semua titik yang memenuhi persamaan ketaksamaan.
Menggambar Grafik Ketaksamaan Linear
Menggambar grafik ketaksamaan linear memiliki langkah-langkah yang mirip dengan menggambar persamaan linear, dengan penambahan satu langkah untuk menentukan daerah penyelesaian.
Contoh soal ketaksamaan seringkali muncul dalam pelajaran matematika, biasanya melibatkan persamaan dengan tanda “lebih besar dari” atau “lebih kecil dari”. Nah, konsep ini mirip dengan kesebangunan dan kekongruenan, yang mempelajari tentang bentuk dan ukuran geometri. Kamu bisa menemukan berbagai contoh soal kesebangunan dan kekongruenan di contoh soal kesebangunan dan kekongruenan.
Contoh soal ketaksamaan pun bisa melibatkan konsep geometri, misalnya mencari luas atau keliling bangun datar yang memenuhi syarat tertentu.
- Ubah ketaksamaan menjadi persamaan linear.
- Tentukan dua titik yang terletak pada garis tersebut.
- Gambar garis yang menghubungkan kedua titik tersebut.
- Tentukan daerah penyelesaian dengan menguji titik (0, 0) atau titik lain yang tidak berada pada garis. Jika titik tersebut memenuhi ketaksamaan, maka daerah yang memuat titik tersebut adalah daerah penyelesaian. Jika tidak, maka daerah yang tidak memuat titik tersebut adalah daerah penyelesaian.
Contoh Soal Ketaksamaan Linear
Misalnya, kita ingin menggambar grafik ketaksamaan 2x + y > 4.
- Ubah ketaksamaan menjadi persamaan linear: 2x + y = 4.
- Tentukan dua titik yang terletak pada garis tersebut. Misalnya, jika x = 0, maka y = 4. Jika y = 0, maka x = 2. Sehingga, kita memiliki titik (0, 4) dan (2, 0).
- Gambar garis yang menghubungkan kedua titik tersebut. Garis tersebut adalah garis yang memiliki persamaan 2x + y = 4.
- Tentukan daerah penyelesaian dengan menguji titik (0, 0). Substitusikan titik (0, 0) ke dalam ketaksamaan 2x + y > 4. Kita peroleh 0 + 0 > 4, yang tidak benar. Sehingga, daerah yang tidak memuat titik (0, 0) adalah daerah penyelesaian.
Gambar grafik ketaksamaan linear 2x + y > 4 akan menunjukkan garis 2x + y = 4 dan daerah yang berada di atas garis tersebut.
Menggambar Grafik Ketaksamaan Kuadrat
Menggambar grafik ketaksamaan kuadrat mirip dengan menggambar grafik persamaan kuadrat, dengan penambahan satu langkah untuk menentukan daerah penyelesaian.
- Ubah ketaksamaan menjadi persamaan kuadrat.
- Tentukan titik potong dengan sumbu x dengan menyelesaikan persamaan kuadrat tersebut.
- Tentukan titik puncak parabola dengan menggunakan rumus x = -b/2a, dan substitusikan nilai x ke dalam persamaan kuadrat untuk memperoleh nilai y.
- Gambar parabola yang melewati titik potong dengan sumbu x dan titik puncak.
- Tentukan daerah penyelesaian dengan menguji titik (0, 0) atau titik lain yang tidak berada pada parabola. Jika titik tersebut memenuhi ketaksamaan, maka daerah yang memuat titik tersebut adalah daerah penyelesaian. Jika tidak, maka daerah yang tidak memuat titik tersebut adalah daerah penyelesaian.
Contoh Soal Ketaksamaan Kuadrat
Misalnya, kita ingin menggambar grafik ketaksamaan y ≤ x² – 4x + 3.
- Ubah ketaksamaan menjadi persamaan kuadrat: y = x² – 4x + 3.
- Tentukan titik potong dengan sumbu x dengan menyelesaikan persamaan kuadrat x² – 4x + 3 = 0. Kita peroleh (x – 1)(x – 3) = 0, sehingga x = 1 atau x = 3. Titik potong dengan sumbu x adalah (1, 0) dan (3, 0).
- Tentukan titik puncak parabola dengan menggunakan rumus x = -b/2a = -(-4)/(2*1) = 2. Substitusikan x = 2 ke dalam persamaan kuadrat, kita peroleh y = 2² – 4*2 + 3 = -1. Titik puncak parabola adalah (2, -1).
- Gambar parabola yang melewati titik potong dengan sumbu x (1, 0) dan (3, 0), serta titik puncak (2, -1). Parabola tersebut terbuka ke atas karena koefisien x² positif.
- Tentukan daerah penyelesaian dengan menguji titik (0, 0). Substitusikan titik (0, 0) ke dalam ketaksamaan y ≤ x² – 4x + 3. Kita peroleh 0 ≤ 0² – 4*0 + 3, yang benar. Sehingga, daerah yang memuat titik (0, 0) adalah daerah penyelesaian.
Gambar grafik ketaksamaan kuadrat y ≤ x² – 4x + 3 akan menunjukkan parabola yang terbuka ke atas dan daerah yang berada di bawah parabola tersebut.
Penerapan Ketaksamaan dalam Kehidupan Sehari-hari
Ketaksamaan merupakan konsep matematika yang sering kita temui dalam kehidupan sehari-hari. Ketaksamaan membantu kita dalam membandingkan dua nilai atau lebih, baik dalam bentuk angka maupun variabel. Dalam kehidupan sehari-hari, penerapan ketaksamaan dapat ditemukan dalam berbagai bidang, seperti ekonomi, sosial, dan sains.
Penerapan Ketaksamaan dalam Masalah Ekonomi
Ketaksamaan memiliki peran penting dalam memahami dinamika ekonomi. Contohnya, dalam analisis ekonomi, ketaksamaan digunakan untuk:
- Membandingkan tingkat pendapatan atau kekayaan antara berbagai kelompok masyarakat.
- Menganalisis distribusi pendapatan dan kekayaan dalam suatu negara.
- Memprediksi dampak kebijakan ekonomi terhadap ketimpangan pendapatan.
Contoh nyata, dalam menentukan tingkat kemiskinan, data statistik menggunakan ketaksamaan untuk membandingkan pendapatan rumah tangga dengan garis kemiskinan yang ditetapkan. Ketaksamaan juga berperan dalam menentukan kebijakan ekonomi, seperti kebijakan pajak progresif, yang bertujuan untuk mengurangi kesenjangan pendapatan.
Penerapan Ketaksamaan dalam Masalah Sosial
Ketaksamaan juga berperan penting dalam memahami dinamika sosial. Berikut beberapa contoh penerapannya:
- Membandingkan tingkat pendidikan, kesehatan, dan akses terhadap layanan publik antara berbagai kelompok masyarakat.
- Menganalisis dampak diskriminasi dan ketidaksetaraan terhadap kelompok minoritas.
- Memprediksi tingkat kesenjangan sosial dan dampaknya terhadap stabilitas masyarakat.
Contohnya, dalam bidang pendidikan, ketaksamaan dapat digunakan untuk membandingkan tingkat akses terhadap pendidikan berkualitas antara kelompok masyarakat yang kaya dan miskin. Ketaksamaan juga dapat digunakan untuk menganalisis dampak diskriminasi terhadap perempuan dalam akses terhadap pekerjaan dan kesempatan.
Penerapan Ketaksamaan dalam Masalah Sains
Ketaksamaan memiliki peran penting dalam berbagai bidang sains, seperti:
- Menentukan batas-batas toleransi dalam eksperimen ilmiah.
- Membandingkan hasil penelitian dan menentukan tingkat signifikansi.
- Membuat model matematika untuk memprediksi fenomena alam.
Contohnya, dalam bidang kimia, ketaksamaan digunakan untuk menentukan konsentrasi larutan yang aman untuk digunakan. Ketaksamaan juga digunakan dalam bidang fisika untuk menganalisis gerak benda dan menentukan batas-batas kecepatan.
Soal Latihan Ketaksamaan
Ketaksamaan merupakan konsep matematika yang penting untuk memahami hubungan antara nilai-nilai. Ketaksamaan digunakan untuk membandingkan nilai dua ekspresi, menentukan rentang nilai, dan memecahkan masalah dalam berbagai bidang, seperti ekonomi, fisika, dan ilmu komputer.
Soal Latihan Ketaksamaan Linear
Ketaksamaan linear adalah ketaksamaan yang melibatkan variabel dengan pangkat tertinggi 1. Berikut adalah beberapa contoh soal ketaksamaan linear:
- Tentukan himpunan penyelesaian dari ketaksamaan 2x + 3 > 7.
- Tentukan nilai x yang memenuhi ketaksamaan 5x – 2 ≤ 13.
- Selesaikan ketaksamaan 3x + 4 < 2x – 1.
- Tentukan himpunan penyelesaian dari ketaksamaan 4x + 5 ≥ 2x – 3.
- Tentukan nilai x yang memenuhi ketaksamaan 2x – 1 > 3x + 2.
Soal Latihan Ketaksamaan Kuadrat
Ketaksamaan kuadrat adalah ketaksamaan yang melibatkan variabel dengan pangkat tertinggi 2. Berikut adalah beberapa contoh soal ketaksamaan kuadrat:
- Tentukan himpunan penyelesaian dari ketaksamaan x² + 2x – 3 < 0.
- Tentukan nilai x yang memenuhi ketaksamaan 2x² – 5x + 3 ≥ 0.
- Selesaikan ketaksamaan x² – 4x + 4 > 0.
- Tentukan himpunan penyelesaian dari ketaksamaan 3x² + 7x + 2 ≤ 0.
- Tentukan nilai x yang memenuhi ketaksamaan -x² + 3x – 2 < 0.
Soal Penerapan Ketaksamaan dalam Kehidupan Sehari-hari
Ketaksamaan dapat diterapkan dalam berbagai situasi dalam kehidupan sehari-hari. Berikut adalah beberapa contoh soal yang menunjukkan penerapan ketaksamaan:
- Seorang tukang jahit memiliki 10 meter kain. Dia ingin membuat kemeja dan celana. Kemeja membutuhkan 1,5 meter kain dan celana membutuhkan 2 meter kain. Berapa banyak kemeja dan celana yang dapat dibuat oleh tukang jahit tersebut?
- Sebuah perusahaan menghasilkan produk A dan produk B. Produk A membutuhkan 3 jam untuk diproduksi dan produk B membutuhkan 2 jam untuk diproduksi. Perusahaan memiliki 120 jam kerja per minggu. Berapa banyak produk A dan produk B yang dapat diproduksi perusahaan tersebut per minggu?
- Seorang pedagang menjual dua jenis buah, yaitu apel dan jeruk. Apel dijual dengan harga Rp 10.000 per kg dan jeruk dijual dengan harga Rp 8.000 per kg. Pedagang tersebut ingin mendapatkan keuntungan minimal Rp 50.000. Berapa kg apel dan jeruk yang harus dijual pedagang tersebut?
- Sebuah perusahaan memiliki budget Rp 100.000.000 untuk membeli 2 jenis mesin, yaitu mesin A dan mesin B. Mesin A berharga Rp 30.000.000 per unit dan mesin B berharga Rp 20.000.000 per unit. Berapa banyak mesin A dan mesin B yang dapat dibeli perusahaan tersebut?
- Seorang siswa ingin mendapatkan nilai rata-rata minimal 80 dalam mata pelajaran matematika. Dia telah mendapatkan nilai 75 dan 85 dalam dua ujian sebelumnya. Berapa nilai minimal yang harus dia dapatkan dalam ujian ketiga agar mencapai target nilai rata-rata?
Tips Mengerjakan Soal Ketaksamaan
Ketaksamaan merupakan salah satu konsep penting dalam matematika yang sering muncul dalam berbagai soal. Memahami konsep ketaksamaan dan menguasai teknik penyelesaiannya akan sangat membantu dalam menyelesaikan soal-soal matematika, terutama dalam aljabar dan kalkulus. Artikel ini akan membahas beberapa tips untuk menyelesaikan soal ketaksamaan, baik linear maupun kuadrat, serta penerapannya dalam kehidupan sehari-hari.
Tips Mengerjakan Soal Ketaksamaan Linear
Ketaksamaan linear melibatkan variabel dengan pangkat tertinggi 1. Untuk menyelesaikan soal ketaksamaan linear, berikut beberapa tips yang dapat membantu:
- Tentukan tanda ketaksamaan. Perhatikan apakah tanda ketaksamaan adalah “lebih besar dari” (>), “lebih kecil dari” (<), "lebih besar dari atau sama dengan" (≥), atau "lebih kecil dari atau sama dengan" (≤).
- Selesaikan persamaan yang terkait. Cari solusi untuk persamaan yang terkait dengan ketaksamaan. Misalnya, jika ketaksamaan adalah x + 2 > 5, maka persamaan yang terkait adalah x + 2 = 5.
- Tentukan arah garis bilangan. Jika tanda ketaksamaan adalah “lebih besar dari” atau “lebih besar dari atau sama dengan”, maka garis bilangan akan diarahkan ke kanan. Jika tanda ketaksamaan adalah “lebih kecil dari” atau “lebih kecil dari atau sama dengan”, maka garis bilangan akan diarahkan ke kiri.
- Tuliskan solusi dalam bentuk interval. Solusi ketaksamaan dapat dituliskan dalam bentuk interval. Misalnya, solusi untuk x + 2 > 5 adalah x > 3, yang dapat dituliskan sebagai interval (3, ∞).
Tips Mengerjakan Soal Ketaksamaan Kuadrat
Ketaksamaan kuadrat melibatkan variabel dengan pangkat tertinggi 2. Berikut beberapa tips untuk menyelesaikan soal ketaksamaan kuadrat:
- Tentukan tanda ketaksamaan. Perhatikan apakah tanda ketaksamaan adalah “lebih besar dari” (>), “lebih kecil dari” (<), "lebih besar dari atau sama dengan" (≥), atau "lebih kecil dari atau sama dengan" (≤).
- Selesaikan persamaan kuadrat yang terkait. Cari solusi untuk persamaan kuadrat yang terkait dengan ketaksamaan. Misalnya, jika ketaksamaan adalah x2 – 4x + 3 > 0, maka persamaan kuadrat yang terkait adalah x2 – 4x + 3 = 0.
- Tentukan interval yang memenuhi ketaksamaan. Gunakan solusi persamaan kuadrat untuk membagi garis bilangan menjadi beberapa interval. Kemudian, uji setiap interval dengan memilih titik uji di setiap interval dan substitusikan ke dalam ketaksamaan awal. Jika titik uji memenuhi ketaksamaan, maka interval tersebut merupakan solusi.
- Tuliskan solusi dalam bentuk interval. Solusi ketaksamaan kuadrat dapat dituliskan dalam bentuk interval. Misalnya, solusi untuk x2 – 4x + 3 > 0 adalah x < 1 atau x > 3, yang dapat dituliskan sebagai interval (-∞, 1) U (3, ∞).
Tips Mengerjakan Soal Penerapan Ketaksamaan dalam Kehidupan Sehari-hari
Ketaksamaan memiliki banyak penerapan dalam kehidupan sehari-hari. Berikut beberapa tips untuk menyelesaikan soal penerapan ketaksamaan:
- Identifikasi variabel dan batasan. Tentukan variabel yang terlibat dalam masalah dan batasan yang diberikan.
- Tuliskan ketaksamaan yang sesuai. Terjemahkan batasan dan informasi dalam masalah ke dalam bentuk ketaksamaan matematika.
- Selesaikan ketaksamaan. Gunakan teknik penyelesaian ketaksamaan yang telah dipelajari untuk mencari solusi ketaksamaan.
- Interpretasikan solusi dalam konteks masalah. Jelaskan solusi dalam konteks masalah dan pastikan solusinya masuk akal.
Sifat-sifat Ketaksamaan
Ketaksamaan merupakan pernyataan matematis yang membandingkan dua nilai atau ekspresi yang tidak sama. Sifat-sifat ketaksamaan membantu kita dalam memahami dan menyelesaikan masalah yang melibatkan ketaksamaan. Sifat-sifat ini berlaku untuk berbagai jenis ketaksamaan, termasuk ketaksamaan linear, ketaksamaan mutlak, dan ketaksamaan dengan variabel di kedua sisi.
Sifat-sifat Dasar Ketaksamaan
Sifat-sifat dasar ketaksamaan merupakan dasar untuk memahami dan menyelesaikan ketaksamaan. Berikut adalah beberapa sifat dasar yang perlu dipahami:
- Jika a > b, maka a + c > b + c. Artinya, jika kita menambahkan nilai yang sama ke kedua sisi ketaksamaan, tanda ketaksamaan tetap sama.
- Jika a > b, maka a – c > b – c. Artinya, jika kita mengurangkan nilai yang sama dari kedua sisi ketaksamaan, tanda ketaksamaan tetap sama.
- Jika a > b dan c > 0, maka ac > bc. Artinya, jika kita mengalikan kedua sisi ketaksamaan dengan nilai positif, tanda ketaksamaan tetap sama.
- Jika a > b dan c < 0, maka ac < bc. Artinya, jika kita mengalikan kedua sisi ketaksamaan dengan nilai negatif, tanda ketaksamaan berbalik.
- Jika a > b dan b > c, maka a > c. Artinya, jika a lebih besar dari b dan b lebih besar dari c, maka a juga lebih besar dari c.
Sifat-sifat Ketaksamaan Mutlak
Ketaksamaan mutlak melibatkan nilai absolut, yang menyatakan jarak suatu nilai dari nol. Sifat-sifat ini membantu kita dalam menyelesaikan ketaksamaan yang melibatkan nilai absolut.
- Jika |a| < b, maka -b < a < b. Artinya, jika nilai absolut dari a lebih kecil dari b, maka a terletak di antara -b dan b.
- Jika |a| > b, maka a < -b atau a > b. Artinya, jika nilai absolut dari a lebih besar dari b, maka a lebih kecil dari -b atau lebih besar dari b.
Sifat-sifat Ketaksamaan Linear
Ketaksamaan linear merupakan ketaksamaan yang melibatkan variabel dengan pangkat tertinggi satu. Sifat-sifat ini membantu kita dalam menyelesaikan ketaksamaan linear dan menentukan solusi yang memenuhi ketaksamaan tersebut.
- Jika ax + b > 0 dan a > 0, maka x > -b/a. Artinya, jika koefisien variabel x positif, maka solusi ketaksamaan adalah x lebih besar dari -b/a.
- Jika ax + b > 0 dan a < 0, maka x < -b/a. Artinya, jika koefisien variabel x negatif, maka solusi ketaksamaan adalah x lebih kecil dari -b/a.
Penutupan
Melalui pemahaman tentang ketaksamaan, kita dapat menyelesaikan berbagai masalah yang kompleks dalam berbagai bidang. Kemampuan untuk menganalisis dan menyelesaikan ketaksamaan tidak hanya berguna dalam dunia akademis, tetapi juga dalam kehidupan sehari-hari. Dengan memahami konsep ini, kita dapat membuat keputusan yang lebih tepat dan efektif dalam berbagai situasi.






