Contoh soal matematika kelas 10 semester 1 – Matematika kelas 10 semester 1, sebuah petualangan seru di dunia angka dan rumus! Di semester ini, kamu akan menjelajahi berbagai konsep matematika yang penting untuk memahami ilmu pengetahuan lainnya. Mulai dari aljabar yang mengungkap rahasia persamaan hingga trigonometri yang mengupas misteri sudut dan segitiga, setiap bab menawarkan tantangan dan kesenangan tersendiri.
Untuk membantu kamu menaklukkan setiap rintangan dan meraih kesuksesan dalam ujian, kami telah merangkum contoh soal matematika kelas 10 semester 1 yang mencakup berbagai materi. Mulai dari pemahaman dasar hingga aplikasi matematika dalam kehidupan sehari-hari, contoh soal ini akan membantumu mengasah kemampuan dan meningkatkan pemahamanmu.
Pengertian dan Ruang Lingkup Matematika Kelas 10 Semester 1: Contoh Soal Matematika Kelas 10 Semester 1
Matematika kelas 10 semester 1 merupakan fondasi penting untuk memahami konsep matematika tingkat lanjut di masa mendatang. Materi-materi yang dipelajari di semester ini akan membantu siswa dalam mengembangkan kemampuan berpikir logis, analitis, dan pemecahan masalah. Pelajaran ini juga akan mempersiapkan siswa untuk menghadapi tantangan di bidang sains, teknologi, dan berbagai bidang lainnya.
Contoh soal matematika kelas 10 semester 1 bisa mencakup berbagai materi, seperti persamaan linear, sistem persamaan linear, dan fungsi. Nah, buat kamu yang ingin memahami alur penyelesaian suatu masalah secara sistematis, bisa banget belajar dari contoh soal flowchart.
Flowchart sendiri bisa membantu kamu memvisualisasikan langkah-langkah penyelesaian suatu masalah, termasuk soal matematika kelas 10. Dengan memahami konsep flowchart, kamu akan lebih mudah dalam menyelesaikan soal-soal matematika yang kompleks.
Materi Pokok Matematika Kelas 10 Semester 1
Berikut adalah beberapa materi pokok yang dipelajari dalam matematika kelas 10 semester 1:
- Logika Matematika: Materi ini membahas tentang konsep dasar logika, pernyataan, implikasi, konvers, invers, kontraposisi, tautologi, kontradiksi, dan kesetaraan logika. Siswa belajar untuk menganalisis dan menyusun argumen secara logis.
- Himpunan: Materi ini membahas tentang pengertian himpunan, jenis-jenis himpunan, operasi himpunan, dan diagram Venn. Siswa belajar untuk mengidentifikasi dan mengklasifikasikan himpunan, serta melakukan operasi himpunan.
- Relasi dan Fungsi: Materi ini membahas tentang pengertian relasi, jenis-jenis relasi, fungsi, jenis-jenis fungsi, dan sifat-sifat fungsi. Siswa belajar untuk menentukan relasi dan fungsi, serta mengidentifikasi sifat-sifatnya.
- Sistem Persamaan Linear Dua Variabel: Materi ini membahas tentang cara menyelesaikan sistem persamaan linear dua variabel dengan metode eliminasi, substitusi, dan grafik. Siswa belajar untuk menyelesaikan masalah yang berkaitan dengan sistem persamaan linear dua variabel.
- Matriks: Materi ini membahas tentang pengertian matriks, operasi matriks, determinan matriks, dan invers matriks. Siswa belajar untuk melakukan operasi matriks dan menyelesaikan masalah yang berkaitan dengan matriks.
- Vektor: Materi ini membahas tentang pengertian vektor, operasi vektor, perkalian dot, dan perkalian silang. Siswa belajar untuk memahami konsep vektor dan melakukan operasi vektor.
Contoh Soal Matematika Kelas 10 Semester 1
Berikut adalah contoh soal yang menguji pemahaman siswa tentang konsep dasar matematika kelas 10 semester 1:
Diketahui himpunan A = 1, 2, 3, 4 dan B = 2, 4, 6. Tentukan:
a. A ∪ B
b. A ∩ B
c. A – B
Soal ini menguji pemahaman siswa tentang operasi himpunan, yaitu gabungan, irisan, dan selisih himpunan. Siswa diharapkan mampu mengidentifikasi anggota himpunan A dan B, kemudian menentukan anggota himpunan yang diminta.
Tabel Materi Matematika Kelas 10 Semester 1
| Materi | Deskripsi Singkat | Contoh Soal |
|---|---|---|
| Logika Matematika | Mempelajari konsep dasar logika, pernyataan, implikasi, konvers, invers, kontraposisi, tautologi, kontradiksi, dan kesetaraan logika. | Tentukan nilai kebenaran dari pernyataan berikut: “Jika hari hujan, maka jalanan basah.” |
| Himpunan | Mempelajari pengertian himpunan, jenis-jenis himpunan, operasi himpunan, dan diagram Venn. | Diketahui himpunan A = 1, 2, 3, 4 dan B = 2, 4, 6. Tentukan A ∪ B. |
| Relasi dan Fungsi | Mempelajari pengertian relasi, jenis-jenis relasi, fungsi, jenis-jenis fungsi, dan sifat-sifat fungsi. | Tentukan apakah relasi (1, 2), (2, 3), (3, 4) merupakan fungsi. |
| Sistem Persamaan Linear Dua Variabel | Mempelajari cara menyelesaikan sistem persamaan linear dua variabel dengan metode eliminasi, substitusi, dan grafik. | Selesaikan sistem persamaan berikut: 2x + y = 5 dan x – 2y = 1. |
| Matriks | Mempelajari pengertian matriks, operasi matriks, determinan matriks, dan invers matriks. | Tentukan determinan dari matriks berikut: [[1, 2], [3, 4]]. |
| Vektor | Mempelajari pengertian vektor, operasi vektor, perkalian dot, dan perkalian silang. | Tentukan hasil dari penjumlahan vektor a = (2, 3) dan b = (1, -1). |
Aljabar
Aljabar adalah cabang matematika yang mempelajari simbol dan aturan untuk memanipulasi simbol tersebut. Simbol ini biasanya mewakili angka, tetapi juga dapat mewakili objek matematika lainnya seperti vektor, matriks, dan fungsi. Aljabar sangat penting dalam matematika karena memungkinkan kita untuk memecahkan masalah yang tidak dapat diselesaikan dengan aritmatika saja. Aljabar digunakan dalam berbagai bidang, seperti ilmu komputer, ekonomi, dan fisika.
Persamaan Linear dan Kuadrat
Persamaan linear dan kuadrat adalah dua jenis persamaan aljabar yang paling umum. Persamaan linear adalah persamaan yang memiliki variabel dengan pangkat tertinggi satu, sedangkan persamaan kuadrat adalah persamaan yang memiliki variabel dengan pangkat tertinggi dua.
Persamaan Linear
Persamaan linear dapat diselesaikan dengan menggunakan metode aljabar. Metode ini melibatkan manipulasi persamaan untuk mengisolasi variabel yang ingin kita cari. Berikut adalah langkah-langkah untuk menyelesaikan persamaan linear:
- Sederhanakan kedua sisi persamaan dengan menggabungkan suku-suku yang sejenis.
- Pindahkan semua suku yang mengandung variabel ke satu sisi persamaan dan semua suku konstan ke sisi lainnya.
- Bagilah kedua sisi persamaan dengan koefisien variabel untuk mengisolasi variabel.
Sebagai contoh, mari kita selesaikan persamaan linear berikut:
2x + 5 = 11
- Sederhanakan kedua sisi persamaan: 2x + 5 = 11
- Pindahkan semua suku yang mengandung variabel ke satu sisi persamaan dan semua suku konstan ke sisi lainnya: 2x = 11 – 5
- Bagilah kedua sisi persamaan dengan koefisien variabel untuk mengisolasi variabel: x = 6/2
- Selesaikan: x = 3
Persamaan Kuadrat
Persamaan kuadrat dapat diselesaikan dengan menggunakan berbagai metode, termasuk:
- Faktorisasi
- Rumus kuadrat
- Melengkapi kuadrat
Metode faktorisasi melibatkan pemfaktoran persamaan kuadrat menjadi dua faktor linear. Metode rumus kuadrat melibatkan penggunaan rumus khusus untuk menemukan akar persamaan kuadrat. Metode melengkapi kuadrat melibatkan manipulasi persamaan kuadrat untuk mengubahnya menjadi bentuk kuadrat sempurna.
Sebagai contoh, mari kita selesaikan persamaan kuadrat berikut dengan menggunakan rumus kuadrat:
x² + 2x – 3 = 0
Rumus kuadrat adalah:
x = (-b ± √(b² – 4ac)) / 2a
Di mana a, b, dan c adalah koefisien persamaan kuadrat.
Dalam contoh ini, a = 1, b = 2, dan c = -3. Dengan memasukkan nilai-nilai ini ke dalam rumus kuadrat, kita mendapatkan:
x = (-2 ± √(2² – 4 * 1 * -3)) / 2 * 1
x = (-2 ± √(16)) / 2
x = (-2 ± 4) / 2
Jadi, akar persamaan kuadrat adalah:
x = 1 atau x = -3
Perbandingan Metode Penyelesaian Persamaan Linear dan Kuadrat
Berikut adalah tabel yang membandingkan metode penyelesaian persamaan linear dan kuadrat:
| Metode | Persamaan Linear | Persamaan Kuadrat |
|---|---|---|
| Faktorisasi | Tidak berlaku | Ya |
| Rumus kuadrat | Tidak berlaku | Ya |
| Melengkapi kuadrat | Tidak berlaku | Ya |
| Metode aljabar | Ya | Ya |
Sistem Persamaan Linear Dua Variabel
Sistem persamaan linear dua variabel adalah sistem yang terdiri dari dua persamaan linear dengan dua variabel. Untuk menyelesaikan sistem persamaan linear dua variabel, kita dapat menggunakan metode substitusi atau eliminasi.
Metode Substitusi
Metode substitusi melibatkan penyelesaian salah satu persamaan untuk salah satu variabel dan kemudian mengganti variabel tersebut ke persamaan lainnya. Berikut adalah langkah-langkah untuk menyelesaikan sistem persamaan linear dua variabel dengan menggunakan metode substitusi:
- Selesaikan salah satu persamaan untuk salah satu variabel.
- Ganti variabel tersebut ke persamaan lainnya.
- Selesaikan persamaan yang dihasilkan untuk variabel lainnya.
- Ganti nilai variabel yang ditemukan ke salah satu persamaan awal untuk menemukan nilai variabel lainnya.
Sebagai contoh, mari kita selesaikan sistem persamaan linear dua variabel berikut dengan menggunakan metode substitusi:
x + y = 5
2x – y = 1
- Selesaikan persamaan pertama untuk x: x = 5 – y
- Ganti x ke persamaan kedua: 2(5 – y) – y = 1
- Selesaikan persamaan yang dihasilkan untuk y: 10 – 2y – y = 1; -3y = -9; y = 3
- Ganti nilai y ke persamaan pertama untuk menemukan nilai x: x + 3 = 5; x = 2
Jadi, solusi sistem persamaan linear dua variabel adalah x = 2 dan y = 3.
Metode Eliminasi
Metode eliminasi melibatkan penjumlahan atau pengurangan kedua persamaan dalam sistem untuk menghilangkan salah satu variabel. Berikut adalah langkah-langkah untuk menyelesaikan sistem persamaan linear dua variabel dengan menggunakan metode eliminasi:
- Kalikan kedua persamaan dengan konstanta sehingga koefisien salah satu variabel sama.
- Jumlahkan atau kurangkan kedua persamaan untuk menghilangkan variabel yang koefisiennya sama.
- Selesaikan persamaan yang dihasilkan untuk variabel lainnya.
- Ganti nilai variabel yang ditemukan ke salah satu persamaan awal untuk menemukan nilai variabel lainnya.
Sebagai contoh, mari kita selesaikan sistem persamaan linear dua variabel berikut dengan menggunakan metode eliminasi:
x + y = 5
2x – y = 1
- Kalikan persamaan pertama dengan 2: 2x + 2y = 10
- Jumlahkan kedua persamaan: 2x + 2y + 2x – y = 10 + 1; 4x + y = 11
- Selesaikan persamaan yang dihasilkan untuk x: 4x = 11 – y; x = (11 – y) / 4
- Ganti nilai x ke persamaan pertama untuk menemukan nilai y: (11 – y) / 4 + y = 5; 11 – y + 4y = 20; 3y = 9; y = 3
Jadi, solusi sistem persamaan linear dua variabel adalah x = 2 dan y = 3.
Trigonometri
Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi-sisi segitiga. Trigonometri memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, teknik, dan navigasi.
Definisi Sinus, Cosinus, dan Tangen
Sinus, cosinus, dan tangen adalah tiga fungsi trigonometri dasar yang didefinisikan berdasarkan perbandingan sisi-sisi segitiga siku-siku.
- Sinus (sin) adalah perbandingan panjang sisi di depan sudut terhadap panjang sisi miring.
- Cosinus (cos) adalah perbandingan panjang sisi di samping sudut terhadap panjang sisi miring.
- Tangen (tan) adalah perbandingan panjang sisi di depan sudut terhadap panjang sisi di samping sudut.
Contoh Soal Identitas Trigonometri
Identitas trigonometri adalah persamaan yang berlaku untuk semua nilai sudut. Berikut adalah contoh soal yang melibatkan penggunaan identitas trigonometri dasar:
Soal:
Buktikan bahwa sin² θ + cos² θ = 1
Penyelesaian:
Perhatikan segitiga siku-siku ABC dengan sudut siku-siku di C.
- Sisi di depan sudut θ adalah BC.
- Sisi di samping sudut θ adalah AC.
- Sisi miring adalah AB.
Berdasarkan definisi sinus dan cosinus:
sin θ = BC/AB
cos θ = AC/AB
Kuadratkan kedua ruas persamaan:
sin² θ = BC²/AB²
cos² θ = AC²/AB²
Jumlahkan kedua ruas persamaan:
sin² θ + cos² θ = BC²/AB² + AC²/AB²
Karena BC² + AC² = AB² (teorema Pythagoras), maka:
sin² θ + cos² θ = AB²/AB² = 1
Jadi, terbukti bahwa sin² θ + cos² θ = 1.
Rumus-rumus Trigonometri Dasar
Berikut adalah tabel yang merangkum rumus-rumus trigonometri dasar dan contoh penerapannya:
| Rumus | Contoh Penerapan |
|---|---|
| sin² θ + cos² θ = 1 | Dapat digunakan untuk mencari nilai sinus atau cosinus jika salah satunya diketahui. |
| tan θ = sin θ / cos θ | Dapat digunakan untuk mencari nilai tangen jika nilai sinus dan cosinus diketahui. |
| sin (α + β) = sin α cos β + cos α sin β | Dapat digunakan untuk mencari nilai sinus dari penjumlahan dua sudut. |
| cos (α + β) = cos α cos β – sin α sin β | Dapat digunakan untuk mencari nilai cosinus dari penjumlahan dua sudut. |
| tan (α + β) = (tan α + tan β) / (1 – tan α tan β) | Dapat digunakan untuk mencari nilai tangen dari penjumlahan dua sudut. |
Fungsi
Fungsi merupakan suatu aturan yang menghubungkan setiap anggota himpunan pertama (domain) dengan tepat satu anggota himpunan kedua (kodomain). Konsep fungsi sangat penting dalam matematika dan ilmu pengetahuan karena memungkinkan kita untuk memodelkan hubungan antara variabel-variabel dan memprediksi perilaku sistem.
Jenis-Jenis Fungsi
Fungsi dapat diklasifikasikan menjadi berbagai jenis berdasarkan sifat dan karakteristiknya. Berikut beberapa jenis fungsi yang umum dipelajari di kelas 10:
- Fungsi Linear: Fungsi linear memiliki bentuk umum y = mx + c, di mana m adalah gradien dan c adalah konstanta. Grafik fungsi linear adalah garis lurus.
- Fungsi Kuadrat: Fungsi kuadrat memiliki bentuk umum y = ax^2 + bx + c, di mana a, b, dan c adalah konstanta. Grafik fungsi kuadrat adalah parabola.
- Fungsi Eksponensial: Fungsi eksponensial memiliki bentuk umum y = a^x, di mana a adalah konstanta dan x adalah variabel. Grafik fungsi eksponensial berbentuk kurva yang semakin curam seiring dengan meningkatnya nilai x.
- Fungsi Trigonometri: Fungsi trigonometri melibatkan sudut dan sisi segitiga siku-siku. Contoh fungsi trigonometri adalah sin(x), cos(x), dan tan(x).
Menentukan Domain dan Range Fungsi
Domain suatu fungsi adalah himpunan semua nilai input yang diizinkan untuk fungsi tersebut. Range suatu fungsi adalah himpunan semua nilai output yang mungkin dihasilkan oleh fungsi tersebut. Berikut langkah-langkah menentukan domain dan range fungsi:
- Identifikasi jenis fungsi: Tentukan jenis fungsi yang ingin Anda cari domain dan range-nya. Misalnya, fungsi linear, kuadrat, atau eksponensial.
- Tentukan batasan input: Perhatikan batasan input yang mungkin ada dalam fungsi tersebut. Misalnya, untuk fungsi akar kuadrat, input harus tidak negatif. Untuk fungsi pecahan, input tidak boleh membuat penyebutnya bernilai nol.
- Tentukan batasan output: Perhatikan batasan output yang mungkin ada dalam fungsi tersebut. Misalnya, untuk fungsi eksponensial, output selalu positif. Untuk fungsi trigonometri, output berada dalam rentang tertentu.
Perbandingan Sifat-Sifat Fungsi Linear, Kuadrat, dan Eksponensial
| Sifat | Fungsi Linear | Fungsi Kuadrat | Fungsi Eksponensial |
|---|---|---|---|
| Bentuk Umum | y = mx + c | y = ax^2 + bx + c | y = a^x |
| Grafik | Garis lurus | Parabola | Kurva yang semakin curam |
| Domain | Semua bilangan real | Semua bilangan real | Semua bilangan real |
| Range | Semua bilangan real | Tergantung nilai a | Semua bilangan real positif |
| Gradien | Konstan | Berubah | Berubah |
| Titik potong sumbu y | (0, c) | (0, c) | (0, 1) |
Geometri
Geometri merupakan cabang matematika yang mempelajari tentang bentuk, ukuran, posisi, dan sifat ruang. Dalam geometri, kita akan mempelajari berbagai macam bangun datar, seperti segitiga, persegi panjang, dan lingkaran.
Segitiga
Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Berikut adalah ilustrasi segitiga:
[Gambar segitiga dengan sisi-sisi a, b, c dan sudut-sudut A, B, C]
- Sisi-sisi segitiga dapat memiliki panjang yang berbeda-beda.
- Jumlah ketiga sudut dalam segitiga selalu 180 derajat.
- Segitiga dapat diklasifikasikan berdasarkan panjang sisinya (sama sisi, sama kaki, atau sembarang) atau berdasarkan besar sudutnya (lancip, siku-siku, atau tumpul).
Persegi Panjang
Persegi panjang adalah bangun datar yang memiliki empat sisi dan empat sudut siku-siku. Sisi-sisi yang berhadapan memiliki panjang yang sama. Berikut adalah ilustrasi persegi panjang:
[Gambar persegi panjang dengan sisi-sisi a, b, c, d]
- Sisi-sisi yang berhadapan pada persegi panjang memiliki panjang yang sama.
- Keempat sudut dalam persegi panjang adalah sudut siku-siku (90 derajat).
Lingkaran
Lingkaran adalah bangun datar yang dibentuk oleh semua titik yang berjarak sama dari suatu titik tetap yang disebut pusat lingkaran. Berikut adalah ilustrasi lingkaran:
[Gambar lingkaran dengan titik pusat O dan jari-jari r]
- Jarak dari pusat lingkaran ke setiap titik pada lingkaran disebut jari-jari.
- Garis lurus yang melewati pusat lingkaran dan menghubungkan dua titik pada lingkaran disebut diameter. Diameter adalah dua kali panjang jari-jari.
- Keliling lingkaran adalah jarak total mengelilingi lingkaran. Keliling lingkaran dapat dihitung dengan rumus K = 2πr, di mana K adalah keliling dan r adalah jari-jari.
- Luas lingkaran adalah area yang dibatasi oleh lingkaran. Luas lingkaran dapat dihitung dengan rumus L = πr², di mana L adalah luas dan r adalah jari-jari.
Contoh Soal Geometri
Berikut adalah contoh soal yang melibatkan perhitungan luas dan keliling bangun datar:
Soal 1:
Sebuah segitiga siku-siku memiliki panjang sisi alas 6 cm dan tinggi 8 cm. Hitunglah luas dan keliling segitiga tersebut!
Soal 2:
Sebuah persegi panjang memiliki panjang 10 cm dan lebar 5 cm. Hitunglah luas dan keliling persegi panjang tersebut!
Soal 3:
Sebuah lingkaran memiliki jari-jari 7 cm. Hitunglah luas dan keliling lingkaran tersebut!
Rumus-Rumus Geometri Dasar
Berikut adalah tabel yang merangkum rumus-rumus geometri dasar dan contoh penerapannya:
| Bangun Datar | Rumus Luas | Rumus Keliling | Contoh Penerapan |
|---|---|---|---|
| Segitiga | L = 1/2 x a x t | K = a + b + c | Sebuah segitiga memiliki alas 10 cm dan tinggi 5 cm. Luas segitiga tersebut adalah L = 1/2 x 10 cm x 5 cm = 25 cm². |
| Persegi Panjang | L = p x l | K = 2(p + l) | Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Keliling persegi panjang tersebut adalah K = 2(12 cm + 8 cm) = 40 cm. |
| Lingkaran | L = πr² | K = 2πr | Sebuah lingkaran memiliki jari-jari 5 cm. Luas lingkaran tersebut adalah L = π(5 cm)² = 25π cm². |
Statistika
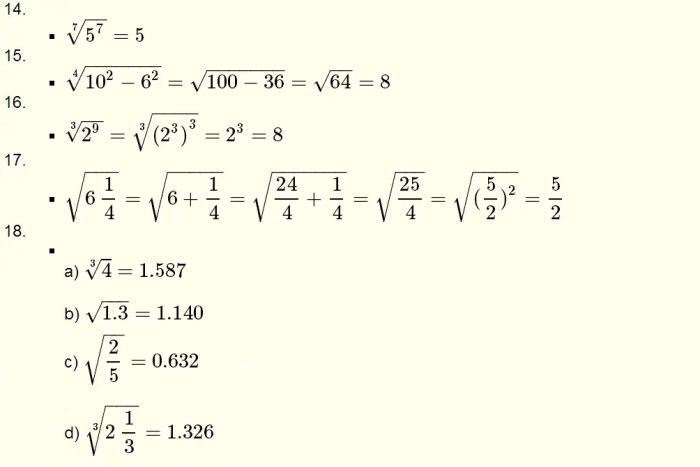
Statistika adalah cabang ilmu matematika yang mempelajari cara mengumpulkan, mengolah, menganalisis, menginterpretasi, dan menyajikan data. Dalam kehidupan sehari-hari, statistika banyak digunakan untuk berbagai keperluan, seperti dalam penelitian, bisnis, dan pemerintahan.
Data, Frekuensi, dan Mean
Data adalah kumpulan informasi yang dikumpulkan dari suatu objek atau kejadian. Data dapat berupa angka, kata, atau simbol. Frekuensi adalah jumlah kemunculan suatu data dalam suatu kumpulan data. Mean adalah nilai rata-rata dari suatu kumpulan data.
Contoh Soal
Misalnya, kita memiliki data nilai ujian matematika dari 5 siswa: 70, 80, 90, 80, dan 70.
- Data: 70, 80, 90, 80, 70
- Frekuensi: 70 muncul 2 kali, 80 muncul 2 kali, 90 muncul 1 kali.
- Mean: (70 + 80 + 90 + 80 + 70) / 5 = 78
Median dan Modus
Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan dari yang terkecil hingga yang terbesar. Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data.
Langkah-langkah Menghitung Median
- Urutkan data dari yang terkecil hingga yang terbesar.
- Jika jumlah data ganjil, maka median adalah nilai tengah.
- Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengah.
Langkah-langkah Menghitung Modus
- Hitung frekuensi kemunculan setiap nilai data.
- Nilai data dengan frekuensi tertinggi adalah modus.
Contoh Soal
Misalnya, kita memiliki data nilai ujian matematika dari 6 siswa: 70, 80, 90, 80, 70, dan 85.
- Data terurut: 70, 70, 80, 80, 85, 90
- Median: (80 + 80) / 2 = 80
- Modus: 80 (muncul 2 kali)
Tabel Perhitungan Mean, Median, dan Modus
| Data | Frekuensi |
|---|---|
| 70 | 2 |
| 80 | 2 |
| 85 | 1 |
| 90 | 1 |
- Mean: (70 * 2 + 80 * 2 + 85 * 1 + 90 * 1) / 6 = 79.17
- Median: (80 + 80) / 2 = 80
- Modus: 80
Peluang
Peluang merupakan konsep matematika yang digunakan untuk mengukur kemungkinan terjadinya suatu kejadian. Dalam kehidupan sehari-hari, kita seringkali menggunakan kata “peluang” untuk menyatakan seberapa besar kemungkinan suatu peristiwa akan terjadi. Misalnya, ketika kita melempar koin, kita memiliki peluang 50% untuk mendapatkan sisi kepala dan peluang 50% untuk mendapatkan sisi ekor.
Jenis-Jenis Peluang
Peluang dapat dibedakan menjadi beberapa jenis, yaitu:
- Peluang Klasik: Peluang klasik dihitung dengan membagi jumlah kejadian yang diinginkan dengan jumlah total kejadian yang mungkin. Misalnya, peluang mendapatkan sisi kepala saat melempar koin adalah 1/2 karena ada 1 sisi kepala dan 2 sisi yang mungkin (kepala atau ekor).
- Peluang Empiris: Peluang empiris dihitung berdasarkan frekuensi relatif suatu kejadian. Misalnya, jika kita melempar koin 100 kali dan mendapatkan sisi kepala sebanyak 55 kali, maka peluang empiris mendapatkan sisi kepala adalah 55/100 atau 0,55.
- Peluang Subjektif: Peluang subjektif didasarkan pada keyakinan atau opini seseorang. Misalnya, jika seseorang merasa yakin bahwa tim sepak bola kesayangannya akan menang, maka ia mungkin memberikan peluang subjektif yang tinggi untuk kemenangan tim tersebut.
Contoh Soal Peluang
Berikut ini adalah contoh soal yang melibatkan perhitungan peluang:
Sebuah kotak berisi 5 bola merah, 3 bola biru, dan 2 bola hijau. Jika diambil satu bola secara acak, berapakah peluang terambilnya bola berwarna merah?
Penyelesaian:
Jumlah total bola dalam kotak adalah 5 + 3 + 2 = 10 bola.
Jumlah bola merah adalah 5.
Oleh karena itu, peluang terambilnya bola merah adalah 5/10 = 1/2.
Peluang Kejadian Majemuk
Peluang kejadian majemuk adalah peluang terjadinya dua atau lebih kejadian secara bersamaan. Ada dua jenis peluang kejadian majemuk, yaitu:
- Peluang Kejadian Bebas: Dua kejadian dikatakan bebas jika terjadinya satu kejadian tidak mempengaruhi terjadinya kejadian lainnya. Misalnya, jika kita melempar koin dua kali, maka hasil lemparan pertama tidak akan mempengaruhi hasil lemparan kedua. Peluang kejadian bebas dihitung dengan mengalikan peluang masing-masing kejadian.
- Peluang Kejadian Tidak Bebas: Dua kejadian dikatakan tidak bebas jika terjadinya satu kejadian mempengaruhi terjadinya kejadian lainnya. Misalnya, jika kita mengambil dua kartu dari satu set kartu remi tanpa pengembalian, maka peluang terambilnya kartu As pada pengambilan kedua akan dipengaruhi oleh kartu yang diambil pada pengambilan pertama. Peluang kejadian tidak bebas dihitung dengan mengalikan peluang kejadian pertama dengan peluang kejadian kedua setelah kejadian pertama terjadi.
Contoh Soal Peluang Kejadian Majemuk
Berikut ini adalah contoh soal yang melibatkan perhitungan peluang kejadian majemuk:
Sebuah dadu dilempar dua kali. Berapakah peluang mendapatkan mata dadu 6 pada lemparan pertama dan mata dadu 4 pada lemparan kedua?
Penyelesaian:
Kejadian mendapatkan mata dadu 6 pada lemparan pertama dan mata dadu 4 pada lemparan kedua adalah kejadian bebas karena hasil lemparan pertama tidak mempengaruhi hasil lemparan kedua.
Peluang mendapatkan mata dadu 6 pada lemparan pertama adalah 1/6.
Peluang mendapatkan mata dadu 4 pada lemparan kedua adalah 1/6.
Oleh karena itu, peluang mendapatkan mata dadu 6 pada lemparan pertama dan mata dadu 4 pada lemparan kedua adalah (1/6) * (1/6) = 1/36.
Rumus-Rumus Peluang
Berikut ini adalah tabel yang merangkum rumus-rumus peluang dan contoh penerapannya:
| Rumus | Contoh Penerapan |
|---|---|
| P(A) = n(A) / n(S) | Peluang mendapatkan sisi kepala saat melempar koin: P(kepala) = 1 / 2 |
| P(A atau B) = P(A) + P(B) – P(A dan B) | Peluang mendapatkan sisi kepala atau sisi ekor saat melempar koin: P(kepala atau ekor) = 1/2 + 1/2 – 0 = 1 |
| P(A dan B) = P(A) * P(B) | Peluang mendapatkan sisi kepala pada lemparan pertama dan sisi ekor pada lemparan kedua saat melempar koin dua kali: P(kepala dan ekor) = 1/2 * 1/2 = 1/4 |
Logaritma
Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen. Logaritma suatu bilangan menyatakan pangkat yang harus diberikan pada basis tertentu untuk mendapatkan bilangan tersebut.
Definisi dan Sifat Logaritma
Logaritma dari suatu bilangan b terhadap basis a, ditulis sebagai logab, didefinisikan sebagai pangkat yang harus diberikan pada a untuk mendapatkan b. Dengan kata lain, jika ax = b, maka logab = x.
Contoh:
* log28 = 3 karena 23 = 8.
* log10100 = 2 karena 102 = 100.
Berikut adalah beberapa sifat penting dari logaritma:
* Sifat 1: loga1 = 0, karena a0 = 1.
* Sifat 2: logaa = 1, karena a1 = a.
* Sifat 3: loga(b × c) = logab + logac.
* Sifat 4: loga(b / c) = logab – logac.
* Sifat 5: logabn = n × logab.
* Sifat 6: logba × logab = 1.
Memecahkan Persamaan Logaritma
Persamaan logaritma adalah persamaan yang melibatkan logaritma. Untuk menyelesaikan persamaan logaritma, kita dapat menggunakan sifat-sifat logaritma untuk mengubah persamaan menjadi bentuk eksponen.
Berikut adalah langkah-langkah umum untuk menyelesaikan persamaan logaritma:
1. Ubah persamaan logaritma menjadi bentuk eksponen.
2. Sederhanakan persamaan.
3. Selesaikan persamaan untuk variabel yang tidak diketahui.
Contoh:
Selesaikan persamaan logaritma berikut:
log2(x + 1) = 3.
1. Ubah persamaan logaritma menjadi bentuk eksponen:
23 = x + 1.
2. Sederhanakan persamaan:
8 = x + 1.
3. Selesaikan persamaan untuk x:
x = 8 – 1 = 7.
Jadi, solusi dari persamaan logaritma log2(x + 1) = 3 adalah x = 7.
Hubungan antara Logaritma dan Eksponen
Logaritma dan eksponen adalah operasi yang saling berlawanan. Hubungan antara logaritma dan eksponen dapat diringkas dalam tabel berikut:
| Eksponen | Logaritma |
|---|---|
| ax = b | logab = x |
Contoh:
* 23 = 8 (eksponen)
* log28 = 3 (logaritma)
Dalam contoh ini, kita dapat melihat bahwa 3 adalah pangkat yang harus diberikan pada 2 untuk mendapatkan 8.
Barisan dan Deret
Barisan dan deret merupakan konsep matematika yang penting dalam aljabar. Barisan adalah urutan bilangan yang tersusun berdasarkan aturan tertentu, sedangkan deret adalah jumlah dari semua suku dalam barisan. Pada artikel ini, kita akan membahas tentang barisan dan deret aritmatika dan geometri, serta bagaimana menentukan suku ke-n dan jumlah n suku pertama dari kedua jenis barisan dan deret tersebut.
Barisan dan Deret Aritmatika
Barisan aritmatika adalah barisan bilangan yang memiliki selisih yang sama antara dua suku yang berurutan. Selisih ini disebut beda. Contoh barisan aritmatika adalah 2, 5, 8, 11, 14, … dengan beda 3.
Deret aritmatika adalah jumlah dari semua suku dalam barisan aritmatika. Contoh deret aritmatika adalah 2 + 5 + 8 + 11 + 14 + …
Menentukan Suku ke-n dan Jumlah n Suku Pertama Barisan Aritmatika
- Suku ke-n (Un)
- a adalah suku pertama
- d adalah beda
- n adalah nomor suku
- Jumlah n Suku Pertama (Sn)
Suku ke-n dari barisan aritmatika dapat ditentukan dengan rumus:
Un = a + (n-1)d
di mana:
Jumlah n suku pertama dari barisan aritmatika dapat ditentukan dengan rumus:
Sn = n/2 (2a + (n-1)d)
atau
Sn = n/2 (a + Un)
Contoh Soal Barisan dan Deret Aritmatika, Contoh soal matematika kelas 10 semester 1
Sebuah barisan aritmatika memiliki suku pertama 3 dan beda 5. Tentukan:
- Suku ke-10
- Jumlah 10 suku pertama
Penyelesaian:
- Suku ke-10 (U10) = a + (n-1)d = 3 + (10-1)5 = 3 + 45 = 48
- Jumlah 10 suku pertama (S10) = n/2 (2a + (n-1)d) = 10/2 (2(3) + (10-1)5) = 5 (6 + 45) = 255
Barisan dan Deret Geometri
Barisan geometri adalah barisan bilangan yang memiliki rasio yang sama antara dua suku yang berurutan. Rasio ini disebut rasio. Contoh barisan geometri adalah 2, 4, 8, 16, 32, … dengan rasio 2.
Deret geometri adalah jumlah dari semua suku dalam barisan geometri. Contoh deret geometri adalah 2 + 4 + 8 + 16 + 32 + …
Menentukan Suku ke-n dan Jumlah n Suku Pertama Barisan Geometri
- Suku ke-n (Un)
- a adalah suku pertama
- r adalah rasio
- n adalah nomor suku
- Jumlah n Suku Pertama (Sn)
- a adalah suku pertama
- r adalah rasio
- n adalah nomor suku
Suku ke-n dari barisan geometri dapat ditentukan dengan rumus:
Un = ar^(n-1)
di mana:
Jumlah n suku pertama dari barisan geometri dapat ditentukan dengan rumus:
Sn = a(1-r^n)/(1-r)
di mana:
Contoh Soal Barisan dan Deret Geometri
Sebuah barisan geometri memiliki suku pertama 2 dan rasio 3. Tentukan:
- Suku ke-5
- Jumlah 5 suku pertama
Penyelesaian:
- Suku ke-5 (U5) = ar^(n-1) = 2(3)^(5-1) = 2(3)^4 = 2(81) = 162
- Jumlah 5 suku pertama (S5) = a(1-r^n)/(1-r) = 2(1-3^5)/(1-3) = 2(-242)/(-2) = 242
Perbandingan Rumus Barisan dan Deret Aritmatika dan Geometri
| Konsep | Aritmatika | Geometri |
|---|---|---|
| Suku ke-n (Un) | Un = a + (n-1)d | Un = ar^(n-1) |
| Jumlah n Suku Pertama (Sn) | Sn = n/2 (2a + (n-1)d) | Sn = a(1-r^n)/(1-r) |
Aplikasi Matematika dalam Kehidupan Sehari-hari
Matematika, seringkali dipandang sebagai mata pelajaran yang kering dan abstrak, ternyata memiliki peran penting dalam kehidupan sehari-hari. Konsep matematika yang kita pelajari di sekolah, seperti aljabar, geometri, kalkulus, dan statistika, ternyata memiliki aplikasi yang luas dan mendalam dalam berbagai bidang kehidupan. Dari bidang ekonomi hingga teknologi, matematika menjadi alat yang ampuh untuk memecahkan masalah, membuat prediksi, dan mengembangkan inovasi.
Contoh Soal Aplikasi Matematika
Berikut adalah contoh soal yang menunjukkan penerapan matematika dalam bidang ekonomi, fisika, dan teknologi:
- Ekonomi: Seorang pengusaha ingin mengetahui keuntungan yang diperoleh dari penjualan produknya. Jika diketahui biaya produksi per unit produk adalah Rp10.000, harga jual per unit adalah Rp15.000, dan jumlah produk yang terjual adalah 100 unit, maka keuntungan yang diperoleh pengusaha tersebut dapat dihitung dengan rumus: Keuntungan = (Harga Jual – Biaya Produksi) x Jumlah Produk Terjual. Dalam hal ini, keuntungan = (Rp15.000 – Rp10.000) x 100 = Rp500.000.
- Fisika: Sebuah mobil melaju dengan kecepatan 72 km/jam. Berapakah jarak yang ditempuh mobil tersebut dalam waktu 2 jam? Untuk menyelesaikan masalah ini, kita dapat menggunakan rumus jarak = kecepatan x waktu. Dalam hal ini, jarak = 72 km/jam x 2 jam = 144 km.
- Teknologi: Seorang programmer ingin membuat program komputer yang dapat menghitung luas persegi panjang. Program tersebut membutuhkan input berupa panjang dan lebar persegi panjang, kemudian menghitung luasnya dengan rumus luas = panjang x lebar. Contohnya, jika panjang persegi panjang adalah 10 cm dan lebarnya 5 cm, maka luasnya adalah 10 cm x 5 cm = 50 cm2.
Langkah-langkah Menyelesaikan Masalah yang Melibatkan Konsep Matematika
Dalam menyelesaikan masalah yang melibatkan konsep matematika dalam kehidupan sehari-hari, kita dapat mengikuti langkah-langkah berikut:
- Memahami masalah: Langkah pertama adalah memahami dengan baik masalah yang ingin kita selesaikan. Apa yang diketahui? Apa yang ingin kita cari? Apa konsep matematika yang relevan dengan masalah tersebut?
- Membuat model matematika: Setelah memahami masalah, kita dapat membuat model matematika yang mewakili masalah tersebut. Model matematika ini dapat berupa persamaan, rumus, atau diagram.
- Memecahkan model matematika: Langkah selanjutnya adalah memecahkan model matematika yang telah dibuat. Kita dapat menggunakan berbagai metode matematika, seperti aljabar, geometri, kalkulus, atau statistika.
- Menginterpretasikan hasil: Setelah mendapatkan solusi dari model matematika, kita perlu menginterpretasikan hasilnya dalam konteks masalah yang kita selesaikan. Apakah hasilnya masuk akal? Apakah hasilnya sesuai dengan harapan kita?
Contoh Aplikasi Matematika dalam Berbagai Bidang Kehidupan
Matematika memiliki aplikasi yang luas dalam berbagai bidang kehidupan. Berikut adalah tabel yang menunjukkan contoh aplikasi matematika dalam berbagai bidang kehidupan:
| Bidang | Contoh Aplikasi |
|---|---|
| Ekonomi | Perhitungan keuntungan, biaya, dan investasi, analisis pasar, prediksi ekonomi |
| Fisika | Perhitungan kecepatan, percepatan, gaya, energi, dan momentum, analisis gerak benda |
| Teknologi | Pembuatan program komputer, pengembangan algoritma, desain sistem komputer, analisis data |
| Kedokteran | Analisis data medis, pengembangan obat, diagnosis penyakit, pemodelan organ tubuh |
| Arsitektur | Desain bangunan, perhitungan struktur, perencanaan tata ruang |
| Seni | Perspektif dalam lukisan, komposisi musik, desain grafis |
Ringkasan Terakhir
Dengan memahami konsep dasar dan berlatih mengerjakan contoh soal, kamu akan semakin siap menghadapi ujian matematika kelas 10 semester 1. Jangan lupa untuk selalu bertanya jika ada materi yang belum dipahami dan teruslah berlatih untuk meraih hasil terbaik! Ingat, matematika bukan hanya tentang rumus, tetapi juga tentang logika, pemecahan masalah, dan kemampuan berpikir kritis. Selamat belajar dan semoga sukses!







