Contoh soal nilai mutlak dan pembahasannya – Nilai mutlak, sebuah konsep matematika yang seringkali ditemui dalam berbagai bidang, mungkin terasa asing bagi sebagian orang. Namun, sebenarnya nilai mutlak merupakan konsep yang sederhana dan mudah dipahami. Dengan memahami definisi, sifat-sifat, dan penerapannya, Anda dapat dengan mudah menyelesaikan soal-soal yang melibatkan nilai mutlak. Artikel ini akan mengajak Anda untuk menjelajahi dunia nilai mutlak melalui contoh soal dan pembahasan yang menarik.
Perjalanan kita akan dimulai dengan memahami definisi nilai mutlak, lalu menjelajahi sifat-sifatnya yang unik. Selanjutnya, kita akan belajar menyelesaikan persamaan dan pertidaksamaan nilai mutlak dengan langkah-langkah yang jelas. Tak hanya itu, kita juga akan melihat bagaimana nilai mutlak berperan penting dalam kehidupan sehari-hari, mulai dari ilmu pengetahuan hingga pemrograman.
Pengertian Nilai Mutlak
Nilai mutlak adalah konsep matematika yang menggambarkan jarak suatu bilangan dari nol pada garis bilangan. Nilai mutlak selalu bernilai positif atau nol, tidak peduli apakah bilangan asalnya positif, negatif, atau nol.
Contoh Nilai Mutlak
Berikut adalah beberapa contoh nilai mutlak dari bilangan positif, negatif, dan nol:
- Nilai mutlak dari 5 adalah 5, karena jarak 5 dari nol pada garis bilangan adalah 5 satuan.
- Nilai mutlak dari -5 adalah 5, karena jarak -5 dari nol pada garis bilangan adalah 5 satuan.
- Nilai mutlak dari 0 adalah 0, karena jarak 0 dari nol pada garis bilangan adalah 0 satuan.
Tabel Nilai Mutlak
Berikut adalah tabel yang menunjukkan nilai mutlak dari beberapa bilangan:
| Bilangan | Nilai Mutlak |
|---|---|
| -5 | 5 |
| -3 | 3 |
| 0 | 0 |
| 2 | 2 |
| 7 | 7 |
Sifat-Sifat Nilai Mutlak
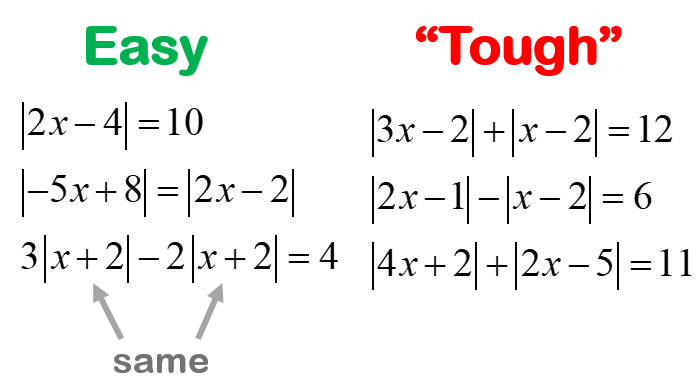
Nilai mutlak, yang dilambangkan dengan tanda garis vertikal (| |), merupakan konsep penting dalam matematika. Nilai mutlak suatu bilangan adalah jarak bilangan tersebut dari nol pada garis bilangan, tanpa memperhatikan arahnya. Sifat-sifat nilai mutlak memungkinkan kita untuk memanipulasi dan menyelesaikan persamaan yang melibatkan nilai mutlak dengan lebih mudah.
Sifat-Sifat Nilai Mutlak, Contoh soal nilai mutlak dan pembahasannya
Berikut adalah beberapa sifat penting dari nilai mutlak:
- Sifat 1: Nilai mutlak selalu non-negatif
Nilai mutlak dari suatu bilangan selalu bernilai nol atau positif. Ini karena jarak dari suatu titik ke nol pada garis bilangan tidak dapat negatif.
|x| ≥ 0 untuk semua x
- Sifat 2: Nilai mutlak dari nol adalah nol
Nilai mutlak dari nol adalah nol, karena jarak nol dari nol pada garis bilangan adalah nol.
|0| = 0
- Sifat 3: Nilai mutlak dari suatu bilangan sama dengan nilai mutlak dari negatifnya
Nilai mutlak dari suatu bilangan dan nilai mutlak dari negatifnya selalu sama. Ini karena jarak dari suatu titik ke nol pada garis bilangan sama dengan jarak dari titik yang berlawanan arah dari nol.
|x| = |-x| untuk semua x
- Sifat 4: Nilai mutlak dari perkalian dua bilangan sama dengan perkalian nilai mutlak dari kedua bilangan tersebut
Sifat ini menunjukkan bahwa nilai mutlak dapat didistribusikan pada perkalian.
|xy| = |x| |y| untuk semua x dan y
- Sifat 5: Nilai mutlak dari hasil bagi dua bilangan sama dengan hasil bagi nilai mutlak dari kedua bilangan tersebut, asalkan penyebutnya tidak nol
Sifat ini menunjukkan bahwa nilai mutlak dapat didistribusikan pada pembagian.
|x/y| = |x| / |y| untuk semua x dan y, dengan y ≠ 0
Penerapan Sifat Nilai Mutlak dalam Menyelesaikan Persamaan
Sifat-sifat nilai mutlak dapat digunakan untuk menyelesaikan persamaan yang melibatkan nilai mutlak. Berikut adalah contoh penerapannya:
Misalkan kita ingin menyelesaikan persamaan |x – 2| = 5. Kita dapat menggunakan sifat nilai mutlak untuk memecahkan persamaan ini.
Berdasarkan sifat 3, kita tahu bahwa |x – 2| = |-(x – 2)| = |2 – x|. Oleh karena itu, kita dapat menulis persamaan tersebut sebagai:
|x – 2| = 5
|2 – x| = 5
Sekarang, kita dapat menyelesaikan persamaan ini dengan menggunakan definisi nilai mutlak. Definisi nilai mutlak menyatakan bahwa:
Jika |x| = a, maka x = a atau x = -a
Berdasarkan definisi ini, kita dapat menuliskan dua kemungkinan solusi untuk persamaan |x – 2| = 5:
Kemungkinan 1: x – 2 = 5
Kemungkinan 2: x – 2 = -5
Dengan menyelesaikan kedua kemungkinan ini, kita mendapatkan solusi untuk persamaan |x – 2| = 5:
x = 7 atau x = -3
Oleh karena itu, solusi dari persamaan |x – 2| = 5 adalah x = 7 atau x = -3.
Menyelesaikan Persamaan Nilai Mutlak
Persamaan nilai mutlak adalah persamaan yang melibatkan nilai mutlak dari suatu ekspresi. Untuk menyelesaikan persamaan nilai mutlak, kita perlu memahami definisi nilai mutlak dan menerapkannya dalam penyelesaian persamaan.
Menyelesaikan Persamaan Nilai Mutlak Sederhana
Persamaan nilai mutlak sederhana adalah persamaan yang melibatkan nilai mutlak dari suatu variabel tunggal. Contoh soal persamaan nilai mutlak sederhana:
|x| = 5
Untuk menyelesaikan persamaan ini, kita perlu mengingat bahwa nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol. Dengan demikian, persamaan |x| = 5 berarti x berjarak 5 satuan dari nol. Oleh karena itu, solusi dari persamaan ini adalah x = 5 atau x = -5.
Langkah-langkah Menyelesaikan Persamaan Nilai Mutlak
Berikut adalah langkah-langkah umum untuk menyelesaikan persamaan nilai mutlak:
- Isolasi nilai mutlak pada satu sisi persamaan.
- Tulis dua persamaan, satu dengan ekspresi dalam nilai mutlak positif dan satu dengan ekspresi dalam nilai mutlak negatif.
- Selesaikan kedua persamaan.
- Verifikasi solusi dengan mensubstitusikan solusi ke dalam persamaan asli.
Contoh Penyelesaian Persamaan Nilai Mutlak
Sebagai contoh, mari kita selesaikan persamaan nilai mutlak berikut:
|2x – 1| = 3
- Nilai mutlak sudah terisolasi pada satu sisi persamaan.
- Kita tulis dua persamaan:
- 2x – 1 = 3
- 2x – 1 = -3
- Selesaikan kedua persamaan:
- 2x = 4 => x = 2
- 2x = -2 => x = -1
- Verifikasi solusi dengan mensubstitusikan solusi ke dalam persamaan asli:
- Untuk x = 2: |2(2) – 1| = |3| = 3 (benar)
- Untuk x = -1: |2(-1) – 1| = |-3| = 3 (benar)
Jadi, solusi dari persamaan |2x – 1| = 3 adalah x = 2 atau x = -1.
Menyelesaikan Persamaan Nilai Mutlak dengan Metode Grafik
Persamaan nilai mutlak dapat diselesaikan secara grafis dengan menggambar grafik fungsi nilai mutlak dan garis horizontal yang mewakili nilai konstan pada sisi kanan persamaan. Titik potong antara grafik fungsi nilai mutlak dan garis horizontal mewakili solusi persamaan.
Sebagai contoh, mari kita selesaikan persamaan |x| = 2 secara grafis. Grafik fungsi nilai mutlak |x| adalah berbentuk V dengan titik puncak di (0, 0). Garis horizontal y = 2 sejajar dengan sumbu x dan berpotongan dengan sumbu y di titik (0, 2). Titik potong antara grafik |x| dan garis y = 2 adalah (2, 2) dan (-2, 2). Jadi, solusi dari persamaan |x| = 2 adalah x = 2 atau x = -2.
Menyelesaikan Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak adalah pertidaksamaan yang melibatkan nilai mutlak suatu ekspresi aljabar. Menyelesaikan pertidaksamaan nilai mutlak melibatkan beberapa langkah yang perlu dipahami dengan baik.
Contoh Soal Pertidaksamaan Nilai Mutlak Sederhana
Sebagai contoh, perhatikan pertidaksamaan nilai mutlak berikut:
|x – 2| < 5
Langkah-langkah Menyelesaikan Pertidaksamaan Nilai Mutlak
Berikut adalah langkah-langkah umum untuk menyelesaikan pertidaksamaan nilai mutlak:
- Tentukan nilai mutlak yang terlibat dalam pertidaksamaan. Dalam contoh di atas, nilai mutlak yang terlibat adalah |x – 2|.
- Tentukan batas-batas nilai yang memenuhi pertidaksamaan. Untuk pertidaksamaan |x – 2| < 5, batas-batas nilai adalah -5 < x - 2 < 5.
- Selesaikan pertidaksamaan dengan memanipulasi batas-batas nilai yang diperoleh. Dalam contoh ini, kita tambahkan 2 ke setiap bagian pertidaksamaan sehingga diperoleh -3 < x < 7.
- Tuliskan solusi dalam bentuk interval. Solusi pertidaksamaan |x – 2| < 5 adalah x ∈ (-3, 7).
Metode Interval
Metode interval adalah salah satu cara untuk menyelesaikan pertidaksamaan nilai mutlak. Metode ini melibatkan pembagian garis bilangan menjadi beberapa interval berdasarkan titik-titik kritis, yaitu titik-titik yang membuat nilai mutlak sama dengan nol.
Contoh Penyelesaian Pertidaksamaan Nilai Mutlak dengan Metode Interval
Misalkan kita ingin menyelesaikan pertidaksamaan |x – 3| > 2 dengan metode interval.
- Tentukan titik kritis. Dalam kasus ini, titik kritis adalah x = 3, karena |x – 3| = 0 ketika x = 3.
- Bagilah garis bilangan menjadi interval-interval berdasarkan titik kritis. Garis bilangan akan terbagi menjadi dua interval: x < 3 dan x > 3.
- Pilih nilai uji dari setiap interval dan substitusikan ke dalam pertidaksamaan asli.
- Untuk interval x < 3, kita bisa memilih x = 0. Substitusikan x = 0 ke dalam pertidaksamaan |x - 3| > 2, kita dapatkan |0 – 3| > 2, yang benar. Jadi, interval x < 3 memenuhi pertidaksamaan.
- Untuk interval x > 3, kita bisa memilih x = 4. Substitusikan x = 4 ke dalam pertidaksamaan |x – 3| > 2, kita dapatkan |4 – 3| > 2, yang salah. Jadi, interval x > 3 tidak memenuhi pertidaksamaan.
- Tuliskan solusi dalam bentuk interval. Solusi pertidaksamaan |x – 3| > 2 adalah x ∈ (-∞, 3) ∪ (3, ∞).
Penerapan Nilai Mutlak dalam Kehidupan Sehari-hari
Nilai mutlak, yang dilambangkan dengan tanda garis vertikal (| |), merupakan konsep matematika yang penting dan memiliki aplikasi luas dalam berbagai bidang, mulai dari ilmu pengetahuan hingga kehidupan sehari-hari. Nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol pada garis bilangan, tanpa memperhatikan arah. Dengan kata lain, nilai mutlak selalu bernilai positif atau nol.
Penerapan Nilai Mutlak dalam Ilmu Pengetahuan
Nilai mutlak memiliki peran penting dalam berbagai bidang ilmu pengetahuan, terutama dalam ilmu fisika dan matematika. Dalam fisika, nilai mutlak digunakan untuk mengukur besaran yang tidak memiliki arah, seperti kecepatan, percepatan, dan gaya. Misalnya, kecepatan mobil yang bergerak ke arah timur dengan kecepatan 60 km/jam sama dengan kecepatan mobil yang bergerak ke arah barat dengan kecepatan 60 km/jam.
- Dalam fisika, nilai mutlak digunakan untuk mengukur besarnya gaya, kecepatan, dan percepatan, tanpa memperhatikan arahnya. Misalnya, nilai mutlak dari gaya gravitasi yang bekerja pada benda adalah sama, baik benda tersebut bergerak ke atas atau ke bawah.
- Dalam matematika, nilai mutlak digunakan untuk menentukan jarak antara dua titik pada garis bilangan atau dalam ruang. Misalnya, jarak antara titik -3 dan 3 pada garis bilangan adalah 6, yang merupakan nilai mutlak dari selisih kedua titik tersebut.
Penerapan Nilai Mutlak dalam Pengukuran dan Pemodelan
Nilai mutlak digunakan dalam berbagai macam pengukuran dan pemodelan. Dalam statistik, nilai mutlak digunakan untuk menghitung deviasi absolut, yaitu selisih antara nilai data dan nilai rata-rata. Dalam ilmu komputer, nilai mutlak digunakan dalam algoritma pencarian dan pengurutan data.
- Dalam pengukuran kesalahan, nilai mutlak digunakan untuk menentukan besarnya kesalahan pengukuran. Misalnya, jika seseorang mengukur panjang meja dengan hasil 1,5 meter, tetapi panjang sebenarnya adalah 1,52 meter, maka kesalahan pengukurannya adalah 0,02 meter, yang merupakan nilai mutlak dari selisih kedua hasil pengukuran tersebut.
- Dalam pemodelan matematika, nilai mutlak digunakan untuk menentukan besarnya selisih antara nilai model dan nilai sebenarnya. Misalnya, jika model matematika memprediksi harga saham tertentu pada hari tertentu adalah Rp10.000, tetapi harga sebenarnya adalah Rp10.200, maka selisih antara nilai model dan nilai sebenarnya adalah Rp200, yang merupakan nilai mutlak dari selisih kedua nilai tersebut.
Contoh Penerapan Nilai Mutlak dalam Berbagai Bidang
| Bidang | Contoh Penerapan Nilai Mutlak |
|---|---|
| Fisika | Mengukur kecepatan dan percepatan tanpa memperhatikan arahnya. |
| Matematika | Menentukan jarak antara dua titik pada garis bilangan atau dalam ruang. |
| Statistik | Menghitung deviasi absolut dalam analisis data. |
| Ilmu Komputer | Menggunakan nilai mutlak dalam algoritma pencarian dan pengurutan data. |
| Keuangan | Menghitung kerugian atau keuntungan dalam transaksi keuangan. |
| Teknik | Mengukur toleransi dalam desain dan manufaktur. |
Contoh Soal Nilai Mutlak dan Pembahasannya
Nilai mutlak merupakan konsep penting dalam matematika yang sering muncul dalam berbagai soal. Untuk menguasai konsep nilai mutlak, latihan soal sangatlah penting. Berikut ini beberapa contoh soal nilai mutlak dengan berbagai tingkat kesulitan dan pembahasannya.
Soal Latihan Nilai Mutlak
Berikut adalah 5 soal latihan tentang nilai mutlak dengan berbagai tingkat kesulitan:
- Tentukan nilai dari | -5 |.
- Selesaikan persamaan | x + 2 | = 5.
- Tentukan himpunan penyelesaian dari pertidaksamaan | 2x – 3 | < 7.
- Tentukan nilai minimum dari fungsi f(x) = | x – 2 | + | x + 3 |.
- Diberikan persamaan | x – 3 | = | 2x + 1 |. Tentukan nilai x yang memenuhi persamaan tersebut.
Kunci Jawaban Soal Latihan Nilai Mutlak
Berikut adalah kunci jawaban untuk setiap soal latihan:
- Nilai dari | -5 | adalah 5. Karena nilai mutlak dari suatu bilangan selalu positif.
- Persamaan | x + 2 | = 5 memiliki dua solusi: x = 3 dan x = -7. Karena nilai mutlak dari suatu bilangan adalah jaraknya dari nol, maka | x + 2 | = 5 berarti x + 2 = 5 atau x + 2 = -5.
- Himpunan penyelesaian dari pertidaksamaan | 2x – 3 | < 7 adalah -2 < x < 5. Karena nilai mutlak dari suatu bilangan selalu positif, maka | 2x - 3 | < 7 berarti -7 < 2x - 3 < 7. Dengan menyelesaikan pertidaksamaan tersebut, diperoleh -2 < x < 5.
- Nilai minimum dari fungsi f(x) = | x – 2 | + | x + 3 | adalah 5. Untuk mencari nilai minimum, kita bisa menggunakan sifat nilai mutlak bahwa | a | + | b | ≥ | a + b |. Dengan menggunakan sifat ini, diperoleh f(x) = | x – 2 | + | x + 3 | ≥ | (x – 2) + (x + 3) | = | 2x + 1 |. Nilai minimum dari | 2x + 1 | adalah 0, yang tercapai ketika x = -1/2. Oleh karena itu, nilai minimum dari f(x) adalah 5.
- Persamaan | x – 3 | = | 2x + 1 | memiliki dua solusi: x = 2/3 dan x = 4. Karena nilai mutlak dari suatu bilangan adalah jaraknya dari nol, maka | x – 3 | = | 2x + 1 | berarti x – 3 = 2x + 1 atau x – 3 = -(2x + 1). Dengan menyelesaikan persamaan tersebut, diperoleh x = 2/3 dan x = 4.
Tabel Contoh Soal Nilai Mutlak dan Pembahasannya
| No | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan nilai dari | -5 |. | Nilai dari | -5 | adalah 5. Karena nilai mutlak dari suatu bilangan selalu positif. |
| 2 | Selesaikan persamaan | x + 2 | = 5. | Persamaan | x + 2 | = 5 memiliki dua solusi: x = 3 dan x = -7. Karena nilai mutlak dari suatu bilangan adalah jaraknya dari nol, maka | x + 2 | = 5 berarti x + 2 = 5 atau x + 2 = -5. |
| 3 | Tentukan himpunan penyelesaian dari pertidaksamaan | 2x – 3 | < 7. | Himpunan penyelesaian dari pertidaksamaan | 2x – 3 | < 7 adalah -2 < x < 5. Karena nilai mutlak dari suatu bilangan selalu positif, maka | 2x - 3 | < 7 berarti -7 < 2x - 3 < 7. Dengan menyelesaikan pertidaksamaan tersebut, diperoleh -2 < x < 5. |
| 4 | Tentukan nilai minimum dari fungsi f(x) = | x – 2 | + | x + 3 |. | Nilai minimum dari fungsi f(x) = | x – 2 | + | x + 3 | adalah 5. Untuk mencari nilai minimum, kita bisa menggunakan sifat nilai mutlak bahwa | a | + | b | ≥ | a + b |. Dengan menggunakan sifat ini, diperoleh f(x) = | x – 2 | + | x + 3 | ≥ | (x – 2) + (x + 3) | = | 2x + 1 |. Nilai minimum dari | 2x + 1 | adalah 0, yang tercapai ketika x = -1/2. Oleh karena itu, nilai minimum dari f(x) adalah 5. |
| 5 | Diberikan persamaan | x – 3 | = | 2x + 1 |. Tentukan nilai x yang memenuhi persamaan tersebut. | Persamaan | x – 3 | = | 2x + 1 | memiliki dua solusi: x = 2/3 dan x = 4. Karena nilai mutlak dari suatu bilangan adalah jaraknya dari nol, maka | x – 3 | = | 2x + 1 | berarti x – 3 = 2x + 1 atau x – 3 = -(2x + 1). Dengan menyelesaikan persamaan tersebut, diperoleh x = 2/3 dan x = 4. |
Konsep Nilai Mutlak dalam Grafik
Nilai mutlak, yang dilambangkan dengan tanda garis vertikal (| |), mewakili jarak suatu bilangan dari nol pada garis bilangan. Konsep ini dapat divisualisasikan dengan mudah dalam grafik, memberikan pemahaman yang lebih intuitif tentang bagaimana nilai mutlak bekerja dan bagaimana ia memengaruhi bentuk fungsi.
Visualisasi Nilai Mutlak dalam Grafik
Ketika nilai mutlak diterapkan pada suatu fungsi, grafik fungsi tersebut akan mengalami transformasi. Transformasi ini dapat dijelaskan dengan dua cara:
- Refleksi terhadap sumbu x: Bagian grafik fungsi yang berada di bawah sumbu x akan direfleksikan ke atas sumbu x. Ini karena nilai mutlak selalu menghasilkan nilai non-negatif.
- Perubahan skala: Bagian grafik fungsi yang berada di atas sumbu x akan tetap sama, sedangkan bagian yang berada di bawah sumbu x akan dilipatgandakan terhadap sumbu x. Ini berarti bahwa nilai y yang negatif akan menjadi positif.
Contoh Grafik Fungsi Nilai Mutlak
Misalnya, perhatikan fungsi nilai mutlak y = |x|. Grafik fungsi ini berbentuk V dengan titik puncak di titik (0, 0). Bagian kiri grafik (x < 0) adalah refleksi dari bagian kanan grafik (x > 0) terhadap sumbu y.
Contoh soal nilai mutlak dan pembahasannya memang seru, tapi pernah nggak sih kamu mikirin soal biaya produksi? Kayak misal, gimana cara menghitung biaya variabel per unit? Nah, buat kamu yang penasaran, bisa banget nih cek contoh soal dan pembahasannya di contoh soal menghitung biaya variabel per unit.
Setelah paham soal biaya variabel, kamu bisa lebih gampang lagi ngerjain soal nilai mutlak, karena kamu udah punya bekal ilmu tambahan soal biaya produksi!
Gambar: Grafik fungsi y = |x| berbentuk V dengan titik puncak di titik (0, 0). Bagian kiri grafik (x < 0) adalah refleksi dari bagian kanan grafik (x > 0) terhadap sumbu y.
Jika kita menambahkan konstanta ke dalam fungsi nilai mutlak, misalnya y = |x| + 2, maka grafik fungsi akan bergeser ke atas sejauh 2 satuan. Sebaliknya, jika kita mengurangkan konstanta, misalnya y = |x| – 2, maka grafik fungsi akan bergeser ke bawah sejauh 2 satuan.
Gambar: Grafik fungsi y = |x| + 2 bergeser ke atas sejauh 2 satuan dari grafik fungsi y = |x|. Grafik fungsi y = |x| – 2 bergeser ke bawah sejauh 2 satuan dari grafik fungsi y = |x|.
Demikian pula, jika kita mengalikan fungsi nilai mutlak dengan konstanta, misalnya y = 2|x|, maka grafik fungsi akan diregangkan secara vertikal. Sebaliknya, jika kita membagi fungsi nilai mutlak dengan konstanta, misalnya y = |x|/2, maka grafik fungsi akan dimampatkan secara vertikal.
Gambar: Grafik fungsi y = 2|x| diregangkan secara vertikal dari grafik fungsi y = |x|. Grafik fungsi y = |x|/2 dimampatkan secara vertikal dari grafik fungsi y = |x|.
Hubungan Nilai Mutlak dan Grafik Fungsi
Secara umum, grafik fungsi nilai mutlak selalu simetris terhadap sumbu y. Titik puncak grafik fungsi nilai mutlak berada di titik (0, 0) atau bergeser dari titik tersebut tergantung pada konstanta yang ditambahkan atau dikurangkan dari fungsi. Grafik fungsi nilai mutlak juga selalu berada di atas sumbu x karena nilai mutlak selalu non-negatif.
Memahami hubungan antara nilai mutlak dan grafik fungsi sangat penting untuk menyelesaikan persamaan dan pertidaksamaan yang melibatkan nilai mutlak. Dengan menggunakan grafik, kita dapat dengan mudah menentukan solusi dari persamaan atau pertidaksamaan tersebut.
Soal Cerita Nilai Mutlak
Nilai mutlak merupakan konsep matematika yang penting dalam berbagai bidang, termasuk fisika, teknik, dan ekonomi. Dalam kehidupan sehari-hari, nilai mutlak sering digunakan untuk mengukur jarak, selisih, atau perbedaan. Berikut adalah contoh soal cerita yang melibatkan konsep nilai mutlak:
Soal Cerita Nilai Mutlak
Seorang petani memiliki kebun berbentuk persegi panjang dengan panjang 10 meter dan lebar 5 meter. Petani tersebut ingin membuat pagar di sekeliling kebunnya. Dia ingin membuat pagar yang memiliki jarak tertentu dari tepi kebun. Jarak pagar dari tepi kebun adalah x meter.
Petani tersebut ingin mengetahui panjang pagar yang dibutuhkan untuk membuat pagar di sekeliling kebun.
Bagaimana cara menentukan panjang pagar yang dibutuhkan?
Perbedaan Nilai Mutlak dan Nilai Absolut: Contoh Soal Nilai Mutlak Dan Pembahasannya
Dalam matematika, kita sering kali berhadapan dengan konsep nilai mutlak dan nilai absolut. Meskipun terdengar serupa, keduanya memiliki perbedaan yang penting. Mari kita bahas perbedaan keduanya dan bagaimana mereka digunakan dalam konteks yang berbeda.
Pengertian Nilai Mutlak dan Nilai Absolut
Nilai mutlak dan nilai absolut merupakan konsep yang sering dianggap sama. Namun, sebenarnya keduanya memiliki perbedaan yang penting. Nilai mutlak merujuk pada jarak suatu bilangan dari nol pada garis bilangan, tanpa memperhatikan arahnya. Sementara itu, nilai absolut adalah istilah yang lebih umum dan dapat merujuk pada berbagai konteks, termasuk jarak, besarnya suatu besaran, atau nilai suatu fungsi.
Contoh Penggunaan Nilai Mutlak dan Nilai Absolut
Untuk memahami perbedaan ini, mari kita lihat contoh berikut:
- Nilai mutlak dari -5 adalah 5, karena jarak -5 dari 0 adalah 5 unit.
- Nilai absolut dari kecepatan mobil adalah 60 km/jam, yang menunjukkan besarnya kecepatan mobil tanpa memperhatikan arahnya.
- Nilai absolut dari fungsi f(x) = x2 adalah |f(x)| = x2, yang menunjukkan nilai fungsi tanpa memperhatikan tanda.
Tabel Perbandingan Nilai Mutlak dan Nilai Absolut
| Aspek | Nilai Mutlak | Nilai Absolut |
|---|---|---|
| Pengertian | Jarak suatu bilangan dari nol pada garis bilangan | Istilah umum yang dapat merujuk pada berbagai konteks, termasuk jarak, besarnya suatu besaran, atau nilai suatu fungsi |
| Contoh | |5| = 5, |-5| = 5 | Kecepatan mobil, nilai fungsi, besarnya gaya |
| Simbol | | | | Tidak ada simbol khusus |
Aplikasi Nilai Mutlak dalam Pemrograman
Nilai mutlak, yang dilambangkan dengan tanda “| |”, merupakan konsep matematika yang menghitung jarak suatu bilangan dari nol, tanpa mempertimbangkan arahnya. Dalam pemrograman, nilai mutlak sering digunakan untuk menyelesaikan berbagai masalah yang melibatkan jarak, perbedaan, atau manipulasi data.
Fungsi Nilai Mutlak dalam Pemrograman
Fungsi nilai mutlak tersedia di berbagai bahasa pemrograman. Fungsi ini biasanya disebut sebagai “abs()” atau “math.abs()”. Fungsi ini menerima input berupa angka dan mengembalikan nilai mutlak dari angka tersebut. Misalnya, dalam bahasa Python, kode berikut akan mengembalikan nilai mutlak dari -5:
>>> abs(-5)
5
Contoh Penggunaan Nilai Mutlak dalam Program
Berikut adalah beberapa contoh penggunaan nilai mutlak dalam pemrograman:
- Perhitungan Jarak: Nilai mutlak dapat digunakan untuk menghitung jarak antara dua titik pada sumbu koordinat. Misalnya, untuk menghitung jarak antara titik (2, 3) dan (5, 7), kita dapat menggunakan rumus berikut:
jarak = abs(2 - 5) + abs(3 - 7) - Validasi Input: Nilai mutlak dapat digunakan untuk memvalidasi input pengguna. Misalnya, untuk memastikan bahwa input pengguna berada dalam rentang tertentu, kita dapat menggunakan nilai mutlak untuk memeriksa apakah input tersebut berada di luar rentang yang diizinkan.
- Algoritma Pencarian: Nilai mutlak digunakan dalam algoritma pencarian tertentu, seperti pencarian biner. Algoritma ini bekerja dengan membagi ruang pencarian menjadi dua bagian secara berulang, dan kemudian memilih bagian yang berisi target berdasarkan nilai mutlak perbedaan antara target dan titik tengah ruang pencarian.
Dalam algoritma pencarian biner, nilai mutlak digunakan untuk menentukan bagian ruang pencarian mana yang harus dipilih pada setiap iterasi. Algoritma ini bekerja dengan membagi ruang pencarian menjadi dua bagian secara berulang, dan kemudian memilih bagian yang berisi target berdasarkan nilai mutlak perbedaan antara target dan titik tengah ruang pencarian. Misalnya, jika target adalah 5 dan titik tengah ruang pencarian adalah 3, maka bagian yang berisi target adalah bagian yang berada di sebelah kanan titik tengah, karena nilai mutlak dari (5 – 3) adalah 2, yang lebih besar dari 0.
Ringkasan Terakhir
Dengan memahami nilai mutlak dan penerapannya, Anda dapat menguasai konsep matematika yang penting ini. Artikel ini telah menunjukkan langkah-langkah menyelesaikan soal-soal nilai mutlak, mulai dari persamaan hingga pertidaksamaan. Ingatlah, latihan adalah kunci untuk menguasai konsep. Jangan ragu untuk mencoba menyelesaikan soal-soal latihan yang telah disediakan dan berlatih secara konsisten. Selamat belajar dan semoga sukses!





