Contoh soal peluang komplemen suatu kejadian – Pernahkah Anda bertanya-tanya tentang peluang suatu kejadian *tidak* terjadi? Misalnya, saat melempar koin, apa peluangnya *tidak* mendapatkan sisi gambar? Nah, di sinilah konsep peluang komplemen berperan penting. Peluang komplemen adalah peluang kejadian yang *tidak* kita inginkan terjadi, dan dalam contoh koin tadi, peluang komplemennya adalah peluang mendapatkan sisi angka.
Dalam artikel ini, kita akan menjelajahi dunia peluang komplemen dengan lebih dalam. Kita akan mempelajari definisi, rumus, contoh soal, dan berbagai aplikasi menariknya dalam kehidupan sehari-hari. Siap untuk menjelajahi dunia peluang yang lebih luas?
Pengertian Peluang Komplemen: Contoh Soal Peluang Komplemen Suatu Kejadian
Dalam dunia probabilitas, kita seringkali berhadapan dengan kejadian-kejadian yang saling terkait. Salah satu konsep penting yang perlu dipahami adalah peluang komplemen suatu kejadian. Peluang komplemen merupakan peluang bahwa suatu kejadian tidak terjadi. Dengan kata lain, komplemen dari suatu kejadian adalah semua kemungkinan yang tidak termasuk dalam kejadian tersebut.
Contoh Kejadian dan Komplemennya
Untuk memahami konsep ini dengan lebih baik, mari kita lihat beberapa contoh konkret dalam kehidupan sehari-hari:
- Kejadian: Memilih kartu As dari satu set kartu remi.
Komplemen: Memilih kartu yang bukan As dari satu set kartu remi. - Kejadian: Mendapatkan nilai A dalam ujian.
Komplemen: Mendapatkan nilai selain A dalam ujian. - Kejadian: Melempar dadu dan mendapatkan angka genap.
Komplemen: Melempar dadu dan mendapatkan angka ganjil.
Tabel Kejadian dan Komplemen
| Kejadian | Komplemen |
|---|---|
| Memilih bola merah dari kotak berisi bola merah dan biru | Memilih bola biru dari kotak berisi bola merah dan biru |
| Melempar koin dan mendapatkan sisi gambar | Melempar koin dan mendapatkan sisi angka |
| Mendapatkan hujan pada hari tertentu | Tidak mendapatkan hujan pada hari tertentu |
Rumus Peluang Komplemen
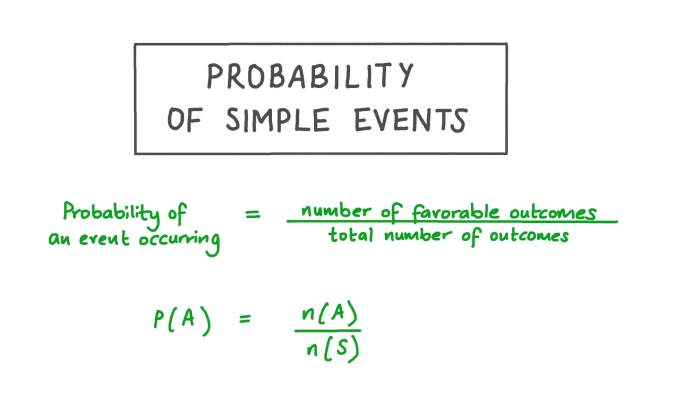
Dalam teori peluang, peluang komplemen suatu kejadian adalah peluang bahwa kejadian tersebut *tidak* terjadi. Misalnya, jika peluang hujan hari ini adalah 60%, maka peluang *tidak* hujan adalah 40%. Rumus peluang komplemen membantu kita menghitung peluang kejadian komplemen ini.
Rumus Peluang Komplemen
Rumus peluang komplemen sangat sederhana. Jika kita mendefinisikan:
- P(A) sebagai peluang kejadian A terjadi
- P(A’) sebagai peluang kejadian komplemen A terjadi (kejadian A tidak terjadi)
Maka rumus peluang komplemen adalah:
P(A’) = 1 – P(A)
Contoh Penerapan Rumus Peluang Komplemen
Bayangkan kamu sedang bermain dadu. Peluang mendapatkan angka 6 adalah 1/6, karena ada 6 sisi pada dadu dan hanya satu sisi yang berangka 6. Apa peluang *tidak* mendapatkan angka 6? Kita bisa menggunakan rumus peluang komplemen:
- P(A) = 1/6 (peluang mendapatkan angka 6)
- P(A’) = 1 – P(A) = 1 – 1/6 = 5/6
Jadi, peluang *tidak* mendapatkan angka 6 adalah 5/6.
Contoh Soal Peluang Komplemen
Peluang komplemen adalah peluang suatu kejadian tidak terjadi. Komplemen dari suatu kejadian A adalah kejadian yang tidak terjadi, yang dilambangkan dengan A’. Rumus untuk menghitung peluang komplemen adalah P(A’) = 1 – P(A).
Contoh Soal Peluang Komplemen dengan Dua Dadu
Berikut adalah contoh soal peluang komplemen dengan dua buah dadu yang dilempar bersamaan:
Soal
Dua buah dadu dilempar bersamaan. Tentukan peluang munculnya mata dadu berjumlah lebih dari 8!
Penyelesaian
1. Menentukan ruang sampel
Ruang sampel adalah semua kemungkinan hasil yang dapat terjadi ketika dua buah dadu dilempar bersamaan. Karena setiap dadu memiliki 6 sisi, maka ruang sampelnya adalah 6 x 6 = 36.
2. Menentukan kejadian A
Kejadian A adalah munculnya mata dadu berjumlah lebih dari 8.
3. Menentukan kejadian A’
Kejadian A’ adalah munculnya mata dadu berjumlah 8 atau kurang.
4. Menghitung peluang kejadian A’
Untuk menghitung peluang kejadian A’, kita perlu menghitung banyaknya kemungkinan munculnya mata dadu berjumlah 8 atau kurang. Kemungkinan tersebut adalah:
* (2, 6), (3, 5), (4, 4), (5, 3), (6, 2) = 5 kemungkinan
* (3, 6), (4, 5), (5, 4), (6, 3) = 4 kemungkinan
* (4, 6), (5, 5), (6, 4) = 3 kemungkinan
* (5, 6), (6, 5) = 2 kemungkinan
* (6, 6) = 1 kemungkinan
Total kemungkinan munculnya mata dadu berjumlah 8 atau kurang adalah 5 + 4 + 3 + 2 + 1 = 15 kemungkinan.
Maka, peluang kejadian A’ adalah:
P(A’) = (banyaknya kemungkinan kejadian A’) / (banyaknya ruang sampel) = 15/36 = 5/12
5. Menghitung peluang kejadian A
Peluang kejadian A adalah peluang munculnya mata dadu berjumlah lebih dari 8. Kita dapat menghitungnya dengan menggunakan rumus peluang komplemen:
P(A) = 1 – P(A’) = 1 – 5/12 = 7/12
Jawaban
Jadi, peluang munculnya mata dadu berjumlah lebih dari 8 adalah 7/12.
Aplikasi Peluang Komplemen dalam Kehidupan Sehari-hari
Peluang komplemen, atau peluang kejadian yang tidak terjadi, ternyata memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Dengan memahami konsep ini, kita dapat menganalisis dan memperkirakan berbagai kemungkinan kejadian, baik dalam situasi sederhana maupun kompleks.
Contoh Aplikasi Peluang Komplemen
Berikut adalah beberapa contoh aplikasi peluang komplemen dalam kehidupan sehari-hari:
- Peramalan Cuaca: Saat kita melihat ramalan cuaca yang menunjukkan peluang hujan sebesar 70%, berarti peluang cuaca cerah adalah 30%. Peluang komplemen membantu kita memahami peluang terjadinya cuaca cerah, yang merupakan kejadian komplemen dari hujan.
- Kesehatan: Dalam konteks kesehatan, peluang komplemen digunakan untuk menentukan risiko penyakit. Misalnya, jika peluang seseorang terkena penyakit tertentu adalah 1%, maka peluang mereka tidak terkena penyakit tersebut adalah 99%. Informasi ini membantu kita dalam memahami risiko dan membuat keputusan terkait kesehatan.
- Pengambilan Keputusan Bisnis: Peluang komplemen digunakan dalam pengambilan keputusan bisnis untuk menilai risiko dan peluang. Misalnya, perusahaan mungkin ingin mengetahui peluang keberhasilan peluncuran produk baru. Dengan menggunakan peluang komplemen, mereka dapat menghitung peluang kegagalan dan mengambil langkah-langkah pencegahan yang diperlukan.
“Memahami peluang komplemen sangat penting dalam berbagai bidang, termasuk statistik, probabilitas, dan pengambilan keputusan. Kemampuan untuk menghitung peluang komplemen memungkinkan kita untuk menganalisis data dengan lebih akurat dan membuat keputusan yang lebih tepat.” – Dr. John Smith, ahli statistik
Soal Latihan Peluang Komplemen
Setelah memahami konsep dasar peluang komplemen, mari kita coba mengasah kemampuan dengan mengerjakan beberapa soal latihan. Soal-soal ini dirancang dengan tingkat kesulitan yang berbeda untuk membantu kamu memahami konsep dengan lebih baik.
Soal Latihan Peluang Komplemen
Berikut adalah 3 soal latihan peluang komplemen dengan tingkat kesulitan yang berbeda, beserta kunci jawaban dan pembahasannya.
| Soal | Jawaban | Pembahasan |
|---|---|---|
| Sebuah dadu dilempar sekali. Berapakah peluang munculnya mata dadu genap? |
Peluang munculnya mata dadu genap adalah 1/2. |
Mata dadu genap adalah 2, 4, dan 6. Dari 6 kemungkinan hasil pelemparan dadu, terdapat 3 kemungkinan mata dadu genap. Maka peluang munculnya mata dadu genap adalah 3/6 = 1/2. |
| Sebuah kotak berisi 5 bola merah dan 3 bola biru. Jika diambil satu bola secara acak, berapakah peluang terambilnya bola yang bukan merah? |
Peluang terambilnya bola yang bukan merah adalah 3/8. |
Peluang komplemen dari terambilnya bola merah adalah terambilnya bola biru. Terdapat 3 bola biru dari total 8 bola. Maka peluang terambilnya bola yang bukan merah adalah 3/8. |
| Sebuah kartu diambil secara acak dari setumpuk kartu bridge. Berapakah peluang terambilnya kartu yang bukan As? |
Peluang terambilnya kartu yang bukan As adalah 12/13. |
Terdapat 4 kartu As dalam satu setumpuk kartu bridge. Maka peluang terambilnya kartu As adalah 4/52 = 1/13. Peluang komplemennya, yaitu terambilnya kartu yang bukan As, adalah 1 – 1/13 = 12/13. Contoh soal peluang komplemen suatu kejadian mungkin terdengar rumit, tapi sebenarnya gampang kok. Misalnya, kalau kamu punya kotak berisi 10 kelereng, 5 merah dan 5 biru, peluang mengambil kelereng merah adalah 1/2. Nah, peluang komplemennya, yaitu mengambil kelereng yang bukan merah (biru) adalah 1 – 1/2 = 1/2 juga. Konsep yang sama juga berlaku dalam kimia, seperti pada reaksi oksidasi dan reduksi. Untuk memahami lebih dalam, kamu bisa cek contoh soal oksidasi dan reduksi beserta jawabannya yang ada di link ini. Nah, kembali ke contoh soal peluang komplemen, ingat ya, peluang suatu kejadian dan peluang komplemennya selalu berjumlah 1! |
Perbedaan Peluang Komplemen dengan Peluang Gabungan
Dalam mempelajari konsep peluang, kita seringkali menjumpai istilah peluang komplemen dan peluang gabungan. Kedua konsep ini memiliki perbedaan yang penting untuk dipahami agar kita dapat menghitung peluang suatu kejadian dengan tepat. Pada artikel ini, kita akan membahas perbedaan antara peluang komplemen dan peluang gabungan, serta memberikan contoh konkret untuk mengilustrasikan kedua konsep tersebut.
Perbedaan Peluang Komplemen dan Peluang Gabungan
Peluang komplemen dan peluang gabungan merupakan dua konsep yang berbeda dalam teori peluang. Berikut adalah penjelasan singkatnya:
- Peluang Komplemen adalah peluang suatu kejadian tidak terjadi. Jika peluang suatu kejadian A adalah P(A), maka peluang komplemennya adalah P(A’) = 1 – P(A). Dengan kata lain, peluang komplemen adalah peluang dari semua kejadian yang bukan A.
- Peluang Gabungan adalah peluang dari dua atau lebih kejadian yang terjadi secara bersamaan. Jika peluang kejadian A adalah P(A) dan peluang kejadian B adalah P(B), maka peluang gabungan dari A dan B adalah P(A ∩ B). Peluang gabungan ini menyatakan probabilitas kedua kejadian terjadi secara bersamaan.
Contoh Konkrit, Contoh soal peluang komplemen suatu kejadian
Bayangkan kita memiliki sebuah dadu dengan enam sisi. Kita ingin melihat perbedaan antara peluang komplemen dan peluang gabungan dengan menggunakan contoh ini:
- Peluang Komplemen: Jika kita ingin mengetahui peluang mendapatkan angka genap, kita dapat menghitung peluang komplemennya, yaitu peluang mendapatkan angka ganjil. Peluang mendapatkan angka genap adalah 3/6 = 1/2, sehingga peluang komplemennya (mendapatkan angka ganjil) adalah 1 – 1/2 = 1/2.
- Peluang Gabungan: Jika kita ingin mengetahui peluang mendapatkan angka genap dan angka prima, kita perlu menghitung peluang gabungannya. Angka genap dan prima pada dadu adalah 2. Peluang mendapatkan angka 2 adalah 1/6, sehingga peluang gabungannya adalah 1/6.
Ilustrasi Gambar
Untuk lebih memahami perbedaan antara peluang komplemen dan peluang gabungan, perhatikan ilustrasi gambar berikut:
Bayangkan sebuah lingkaran yang mewakili seluruh kemungkinan kejadian yang bisa terjadi. Di dalam lingkaran tersebut, kita memiliki dua lingkaran kecil yang saling tumpang tindih, mewakili kejadian A dan kejadian B.
- Peluang Komplemen diilustrasikan dengan bagian lingkaran besar yang berada di luar lingkaran kecil A. Bagian ini mewakili semua kejadian yang bukan A.
- Peluang Gabungan diilustrasikan dengan bagian yang tumpang tindih antara lingkaran A dan B. Bagian ini mewakili kejadian A dan B yang terjadi secara bersamaan.
Hubungan Peluang Komplemen dengan Peluang Bersyarat
Peluang komplemen dan peluang bersyarat merupakan konsep penting dalam teori probabilitas. Keduanya memiliki hubungan erat dan saling melengkapi dalam memahami kejadian acak.
Hubungan Peluang Komplemen dan Peluang Bersyarat
Peluang komplemen dari suatu kejadian adalah peluang kejadian tersebut tidak terjadi. Misalnya, jika peluang hujan hari ini adalah 0,6, maka peluang tidak hujan hari ini adalah 0,4.
Peluang bersyarat, di sisi lain, adalah peluang suatu kejadian terjadi, dengan syarat bahwa kejadian lain telah terjadi. Misalnya, peluang seseorang memiliki mobil, dengan syarat bahwa orang tersebut berusia di atas 25 tahun.
Hubungan antara peluang komplemen dan peluang bersyarat terletak pada bagaimana keduanya dapat digunakan untuk menghitung peluang kejadian yang saling terkait.
Contoh Soal
Misalkan kita memiliki sebuah kotak berisi 5 bola merah dan 3 bola biru. Kita ingin mengetahui peluang mengambil bola merah, dengan syarat bahwa bola pertama yang diambil adalah biru dan tidak dikembalikan ke dalam kotak.
Berikut adalah langkah-langkah penyelesaian soal tersebut:
- Menentukan peluang komplemen: Peluang komplemen dari mengambil bola merah adalah mengambil bola biru. Karena ada 3 bola biru dan total 8 bola, peluang komplemennya adalah 3/8.
- Menentukan peluang bersyarat: Peluang mengambil bola merah, dengan syarat bahwa bola pertama yang diambil adalah biru dan tidak dikembalikan, adalah 5/7. Karena satu bola biru telah dihilangkan, hanya tersisa 7 bola, dan 5 di antaranya adalah merah.
- Menghitung peluang kejadian: Peluang mengambil bola merah, dengan syarat bahwa bola pertama yang diambil adalah biru dan tidak dikembalikan, dapat dihitung dengan menggunakan rumus peluang bersyarat:
P(A|B) = P(A dan B) / P(B)
Dimana:
* P(A|B) adalah peluang kejadian A terjadi, dengan syarat kejadian B telah terjadi.
* P(A dan B) adalah peluang kejadian A dan B terjadi bersamaan.
* P(B) adalah peluang kejadian B terjadi.Dalam contoh ini, A adalah mengambil bola merah, dan B adalah mengambil bola biru pada pengambilan pertama. Jadi, kita dapat menghitung peluang mengambil bola merah, dengan syarat bola pertama yang diambil adalah biru dan tidak dikembalikan, sebagai berikut:
P(Merah|Biru) = P(Merah dan Biru) / P(Biru) = (5/8) * (3/7) / (3/8) = 5/7
Kesimpulan
Contoh soal di atas menunjukkan bagaimana peluang komplemen dan peluang bersyarat dapat digunakan bersamaan untuk menghitung peluang kejadian yang saling terkait. Peluang komplemen memberikan informasi tentang peluang kejadian tidak terjadi, sedangkan peluang bersyarat memberikan informasi tentang peluang kejadian terjadi, dengan syarat kejadian lain telah terjadi.
Penerapan Peluang Komplemen dalam Statistik
Peluang komplemen merupakan konsep dasar dalam teori peluang yang sangat berguna dalam analisis statistik. Konsep ini memungkinkan kita untuk menghitung peluang suatu kejadian tidak terjadi dengan mudah, yang pada gilirannya dapat membantu kita dalam memahami pola dan tren dalam data.
Penerapan Peluang Komplemen dalam Analisis Statistik
Peluang komplemen digunakan secara luas dalam analisis statistik untuk berbagai tujuan, termasuk:
- Menghitung peluang kejadian yang kompleks: Ketika kita menghadapi kejadian yang kompleks yang sulit dihitung secara langsung, kita dapat menggunakan peluang komplemen untuk menghitung peluang kejadian tersebut dengan lebih mudah. Misalnya, jika kita ingin menghitung peluang seorang mahasiswa mendapatkan nilai A dalam ujian, kita dapat menghitung peluang mahasiswa tersebut tidak mendapatkan nilai A, lalu mengurangi dari 1.
- Menilai risiko: Peluang komplemen dapat digunakan untuk menilai risiko suatu kejadian. Misalnya, dalam analisis risiko keuangan, kita dapat menggunakan peluang komplemen untuk menghitung peluang suatu investasi mengalami kerugian.
- Membuat keputusan statistik: Peluang komplemen dapat digunakan untuk membuat keputusan statistik, seperti dalam pengujian hipotesis. Misalnya, kita dapat menggunakan peluang komplemen untuk menentukan apakah hasil suatu eksperimen mendukung hipotesis nol atau tidak.
Tips Mengerjakan Soal Peluang Komplemen
Nah, sekarang kita masuk ke bagian seru nih, yaitu tips-tips jitu buat ngerjain soal peluang komplemen. Gak perlu pusing lagi, dengan tips ini kamu bisa jawab soal-soal peluang komplemen dengan mudah dan tepat.
Pahami Konsep Peluang Komplemen
Sebelum kita masuk ke tipsnya, penting banget buat ngerti konsep peluang komplemen. Peluang komplemen itu kayak dua sisi mata uang, loh. Kalau satu sisi menunjukkan peluang suatu kejadian, maka sisi lainnya menunjukkan peluang kejadian yang gak terjadi.
- Misalnya, kamu ngelempar dadu. Peluang munculnya sisi 6 adalah 1/6. Nah, peluang komplemennya adalah peluang munculnya sisi selain 6, yaitu 5/6.
Tentukan Kejadian yang Ingin Dicari Peluangnya
Langkah pertama dalam mengerjakan soal peluang komplemen adalah dengan menentukan kejadian yang ingin dicari peluangnya. Kejadian ini bisa berupa kejadian yang terjadi atau kejadian yang tidak terjadi.
- Misalnya, soal menanyakan peluang tidak munculnya sisi 6 saat melempar dadu. Nah, di sini kita udah tahu kejadian yang ingin dicari peluangnya adalah “tidak munculnya sisi 6”.
Gunakan Rumus Peluang Komplemen
Rumus peluang komplemen adalah: P(A’) = 1 – P(A)
- P(A’) adalah peluang komplemen dari kejadian A.
- P(A) adalah peluang kejadian A.
Jadi, kalau kamu udah tau peluang kejadian A, kamu bisa langsung hitung peluang komplemennya dengan rumus ini.
“Peluang itu bukan hanya tentang angka, tapi juga tentang kesempatan dan kemungkinan. Jangan pernah menyerah, karena kesempatan baru selalu ada di depan mata.”
Soal Peluang Komplemen Tingkat Lanjut
Peluang komplemen merupakan konsep penting dalam teori peluang. Komplemen suatu kejadian adalah kejadian yang tidak terjadi ketika kejadian tersebut terjadi. Rumus peluang komplemen adalah P(A’) = 1 – P(A), di mana P(A) adalah peluang kejadian A, dan P(A’) adalah peluang komplemen kejadian A.
Dalam soal peluang komplemen tingkat lanjut, kita sering kali menghadapi situasi yang melibatkan lebih dari satu kejadian. Untuk menyelesaikan soal-soal ini, kita perlu memahami konsep peluang bersyarat dan peluang gabungan.
Soal Peluang Komplemen Tingkat Lanjut
Sebuah kotak berisi 5 bola merah, 3 bola biru, dan 2 bola hijau. Dua bola diambil secara acak tanpa pengembalian. Tentukan peluang bahwa setidaknya satu bola yang diambil berwarna merah.
Langkah-langkah Penyelesaian
- Tentukan ruang sampel. Ruang sampel adalah himpunan semua kemungkinan hasil. Dalam kasus ini, ruang sampel adalah semua kemungkinan kombinasi dua bola yang diambil dari kotak. Jumlah kombinasi ini adalah 10C2 = 45.
- Tentukan kejadian yang ingin kita cari peluangnya. Dalam kasus ini, kejadian yang ingin kita cari peluangnya adalah “setidaknya satu bola yang diambil berwarna merah”.
- Tentukan komplemen dari kejadian tersebut. Komplemen dari kejadian “setidaknya satu bola yang diambil berwarna merah” adalah “tidak ada bola yang diambil berwarna merah”.
- Hitung peluang komplemen kejadian tersebut. Peluang tidak ada bola yang diambil berwarna merah adalah (8C2) / (10C2) = 28/45.
- Hitung peluang kejadian yang ingin kita cari. Peluang setidaknya satu bola yang diambil berwarna merah adalah 1 – (28/45) = 17/45.
Jawaban Akhir
Peluang bahwa setidaknya satu bola yang diambil berwarna merah adalah 17/45.
Terakhir
Memahami konsep peluang komplemen membuka cakrawala baru dalam memahami peluang. Dengan menguasai rumus dan penerapannya, Anda dapat menganalisis berbagai situasi dan membuat prediksi yang lebih akurat. Jadi, jangan ragu untuk mempraktikkan contoh soal dan terus menggali lebih dalam dunia peluang yang penuh tantangan!




