Contoh soal substitusi dan eliminasi – Pernahkah Anda merasa kesulitan dalam menyelesaikan sistem persamaan linear dua variabel? Tenang, Anda tidak sendirian! Banyak orang yang merasa kebingungan dengan cara menyelesaikannya. Tapi jangan khawatir, ada dua metode jitu yang bisa membantu Anda, yaitu metode substitusi dan eliminasi.
Metode substitusi dan eliminasi merupakan teknik yang efektif untuk mencari solusi dari sistem persamaan linear dua variabel. Dengan memahami kedua metode ini, Anda akan mampu menyelesaikan berbagai macam soal matematika, baik itu soal cerita, soal ujian, maupun soal yang berkaitan dengan kehidupan sehari-hari.
Pengertian Substitusi dan Eliminasi: Contoh Soal Substitusi Dan Eliminasi
Sistem persamaan linear dua variabel merupakan kumpulan dari dua persamaan linear yang memiliki dua variabel. Untuk menyelesaikan sistem persamaan linear dua variabel, kita dapat menggunakan beberapa metode, salah satunya adalah metode substitusi dan eliminasi. Metode substitusi dan eliminasi merupakan metode yang umum digunakan dalam aljabar untuk mencari nilai variabel dalam sistem persamaan linear. Kedua metode ini memiliki perbedaan dan keunggulan masing-masing.
Metode Substitusi
Metode substitusi merupakan metode untuk menyelesaikan sistem persamaan linear dengan cara mengganti salah satu variabel dalam persamaan dengan nilai variabel lainnya yang diperoleh dari persamaan yang lain. Dengan kata lain, metode substitusi adalah metode yang memanfaatkan ekspresi variabel dalam satu persamaan untuk menggantikan variabel yang sama dalam persamaan lainnya.
Metode Eliminasi
Metode eliminasi merupakan metode untuk menyelesaikan sistem persamaan linear dengan cara menghilangkan salah satu variabel dari sistem persamaan tersebut. Caranya adalah dengan mengalikan kedua persamaan dengan suatu konstanta sehingga koefisien dari salah satu variabel menjadi sama tetapi tanda nya berlawanan, kemudian kedua persamaan dijumlahkan. Dengan demikian, salah satu variabel akan tereliminasi, dan kita dapat mencari nilai variabel yang lain.
Perbedaan Metode Substitusi dan Eliminasi
Metode substitusi dan eliminasi merupakan metode yang efektif untuk menyelesaikan sistem persamaan linear dua variabel. Namun, kedua metode ini memiliki perbedaan yang mendasar, seperti yang ditunjukkan pada ilustrasi berikut:
| Metode | Langkah | Ilustrasi |
|---|---|---|
| Substitusi |
|
Misalkan kita memiliki sistem persamaan:
x + y = 5 Kita dapat menyelesaikan persamaan pertama untuk x: x = 5 – y Kemudian, kita substitusikan nilai x ke dalam persamaan kedua: 2(5 – y) – y = 1 Setelah itu, kita selesaikan persamaan untuk y: y = 3 Terakhir, kita substitusikan nilai y kembali ke persamaan x = 5 – y untuk mendapatkan nilai x: x = 5 – 3 = 2 Jadi, solusi dari sistem persamaan tersebut adalah x = 2 dan y = 3. |
| Eliminasi |
|
Misalkan kita memiliki sistem persamaan:
x + y = 5 Kita dapat mengalikan persamaan pertama dengan -1 sehingga koefisien y menjadi sama tetapi tanda nya berlawanan: -x – y = -5 Kemudian, kita jumlahkan kedua persamaan: x = -4 Terakhir, kita substitusikan nilai x kembali ke persamaan x + y = 5 untuk mendapatkan nilai y: -4 + y = 5 y = 9 Jadi, solusi dari sistem persamaan tersebut adalah x = -4 dan y = 9. |
Metode Substitusi
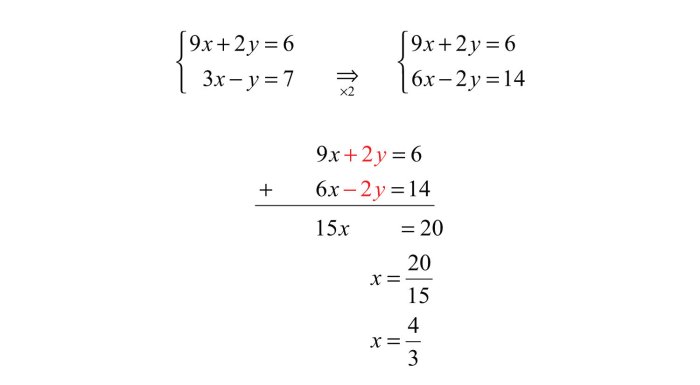
Metode substitusi adalah salah satu metode yang digunakan untuk menyelesaikan sistem persamaan linear dua variabel. Metode ini melibatkan penyelesaian salah satu persamaan terhadap salah satu variabelnya, kemudian substitusikan nilai variabel tersebut ke persamaan lainnya.
Langkah-langkah Metode Substitusi
Berikut adalah langkah-langkah menyelesaikan sistem persamaan linear dua variabel dengan metode substitusi:
| Langkah | Penjelasan |
|---|---|
| 1. Selesaikan salah satu persamaan terhadap salah satu variabelnya. | Misalnya, jika kita memiliki persamaan $x + y = 5$, kita dapat menyelesaikan persamaan tersebut terhadap $x$ dengan cara $x = 5 – y$. |
| 2. Substitusikan nilai variabel yang telah diubah ke persamaan lainnya. | Misalnya, jika kita memiliki persamaan $2x – y = 1$ dan kita telah mendapatkan $x = 5 – y$, kita dapat mensubstitusikan $x$ ke persamaan kedua: $2(5 – y) – y = 1$. |
| 3. Selesaikan persamaan yang baru. | Dalam contoh sebelumnya, kita akan mendapatkan persamaan $10 – 2y – y = 1$, yang dapat disederhanakan menjadi $3y = 9$ dan menghasilkan $y = 3$. |
| 4. Substitusikan nilai variabel yang telah ditemukan ke salah satu persamaan awal untuk mendapatkan nilai variabel lainnya. | Dalam contoh sebelumnya, kita dapat mensubstitusikan $y = 3$ ke persamaan $x + y = 5$ untuk mendapatkan $x + 3 = 5$, sehingga $x = 2$. |
Contoh Soal Sistem Persamaan Linear Dua Variabel yang Dapat Diselesaikan dengan Metode Substitusi
Misalnya, kita memiliki sistem persamaan linear dua variabel berikut:
$x + y = 5$
$2x – y = 1$
Kita dapat menyelesaikan sistem persamaan ini dengan metode substitusi sebagai berikut:
1. Selesaikan persamaan pertama terhadap $x$: $x = 5 – y$.
2. Substitusikan nilai $x$ ke persamaan kedua: $2(5 – y) – y = 1$.
3. Selesaikan persamaan yang baru: $10 – 2y – y = 1$, sehingga $3y = 9$ dan $y = 3$.
4. Substitusikan nilai $y$ ke persamaan pertama: $x + 3 = 5$, sehingga $x = 2$.
Jadi, solusi dari sistem persamaan linear dua variabel tersebut adalah $x = 2$ dan $y = 3$.
Contoh Soal Sistem Persamaan Linear Dua Variabel yang Tidak Dapat Diselesaikan dengan Metode Substitusi
Misalnya, kita memiliki sistem persamaan linear dua variabel berikut:
$x + y = 5$
$2x + 2y = 10$
Sistem persamaan ini tidak dapat diselesaikan dengan metode substitusi karena kedua persamaan tersebut sebenarnya adalah persamaan yang sama. Jika kita menyelesaikan persamaan pertama terhadap $x$, kita akan mendapatkan $x = 5 – y$. Jika kita mensubstitusikan nilai $x$ ke persamaan kedua, kita akan mendapatkan $2(5 – y) + 2y = 10$, yang akan menghasilkan persamaan $10 = 10$. Persamaan ini tidak memberikan informasi baru tentang nilai $x$ atau $y$, sehingga kita tidak dapat menyelesaikan sistem persamaan ini dengan metode substitusi.
Metode Eliminasi
Metode eliminasi merupakan salah satu cara untuk menyelesaikan sistem persamaan linear dua variabel. Metode ini dilakukan dengan cara menghilangkan salah satu variabel dengan cara menjumlahkan atau mengurangkan kedua persamaan yang ada. Tujuannya adalah untuk mendapatkan persamaan baru yang hanya mengandung satu variabel, sehingga nilai variabel tersebut dapat dicari.
Langkah-langkah Metode Eliminasi
Berikut langkah-langkah yang dapat digunakan untuk menyelesaikan sistem persamaan linear dua variabel dengan metode eliminasi:
| Langkah | Penjelasan | Contoh | Catatan |
|---|---|---|---|
| 1. Ubah koefisien salah satu variabel agar sama | Kalikan kedua persamaan dengan konstanta yang sesuai sehingga koefisien salah satu variabel menjadi sama. | Misalnya, jika persamaan pertama adalah 2x + 3y = 7 dan persamaan kedua adalah 4x – 5y = 11, maka koefisien x dapat disamakan dengan mengalikan persamaan pertama dengan 2. | Jika koefisien variabel sudah sama, langkah ini dapat dilewati. |
| 2. Jumlahkan atau kurangkan kedua persamaan | Jumlahkan atau kurangkan kedua persamaan yang sudah memiliki koefisien sama. Jika koefisien variabel yang sama memiliki tanda yang sama, maka kedua persamaan dikurangkan. Sebaliknya, jika koefisien variabel yang sama memiliki tanda yang berbeda, maka kedua persamaan dijumlahkan. | Jika persamaan pertama adalah 4x + 6y = 14 dan persamaan kedua adalah 4x – 5y = 11, maka kedua persamaan dapat dikurangkan untuk menghilangkan variabel x. | Pilih operasi yang akan digunakan (penjumlahan atau pengurangan) berdasarkan tanda koefisien variabel yang sama. |
| 3. Selesaikan persamaan baru untuk mencari nilai variabel | Persamaan baru yang diperoleh setelah penjumlahan atau pengurangan hanya mengandung satu variabel. Selesaikan persamaan tersebut untuk mencari nilai variabel tersebut. | Jika persamaan baru adalah 11y = 3, maka nilai y dapat dicari dengan membagi kedua ruas dengan 11, sehingga diperoleh y = 3/11. | Persamaan baru harus diselesaikan untuk mendapatkan nilai variabel yang tersisa. |
| 4. Substitusikan nilai variabel yang sudah diketahui ke salah satu persamaan awal | Substitusikan nilai variabel yang sudah diketahui ke salah satu persamaan awal untuk mencari nilai variabel yang lain. | Misalnya, jika nilai y = 3/11 dan persamaan awal adalah 2x + 3y = 7, maka nilai y dapat disubstitusikan ke persamaan tersebut untuk mencari nilai x. | Substitusikan nilai variabel yang sudah diketahui ke persamaan awal yang lebih sederhana. |
Contoh Soal Sistem Persamaan Linear Dua Variabel yang Dapat Diselesaikan dengan Metode Eliminasi, Contoh soal substitusi dan eliminasi
Misalnya, kita ingin menyelesaikan sistem persamaan linear dua variabel berikut:
2x + 3y = 7
4x – 5y = 11
Untuk menyelesaikan sistem persamaan ini dengan metode eliminasi, kita dapat melakukan langkah-langkah berikut:
- Kalikan persamaan pertama dengan 2 sehingga koefisien x menjadi sama, yaitu 4x:
- Kurangkan persamaan kedua dari persamaan pertama untuk menghilangkan variabel x:
- Selesaikan persamaan baru untuk mencari nilai y:
- Substitusikan nilai y = 3/11 ke persamaan pertama untuk mencari nilai x:
4x + 6y = 14
(4x + 6y) – (4x – 5y) = 14 – 11
11y = 3
y = 3/11
2x + 3(3/11) = 7
2x + 9/11 = 7
2x = 7 – 9/11
2x = 72/11
x = 36/11
Jadi, solusi dari sistem persamaan linear dua variabel tersebut adalah x = 36/11 dan y = 3/11.
Contoh Soal Sistem Persamaan Linear Dua Variabel yang Tidak Dapat Diselesaikan dengan Metode Eliminasi
Misalnya, kita ingin menyelesaikan sistem persamaan linear dua variabel berikut:
2x + 3y = 7
4x + 6y = 14
Jika kita coba menyelesaikan sistem persamaan ini dengan metode eliminasi, kita akan menemukan bahwa kedua persamaan tersebut merupakan persamaan yang sama. Hal ini terjadi karena persamaan kedua merupakan hasil perkalian persamaan pertama dengan 2. Dengan demikian, kedua persamaan tidak dapat dikurangkan atau dijumlahkan untuk menghilangkan salah satu variabel. Oleh karena itu, sistem persamaan linear dua variabel ini tidak dapat diselesaikan dengan metode eliminasi.
Penerapan Metode Substitusi dan Eliminasi dalam Kehidupan Sehari-hari
Metode substitusi dan eliminasi adalah dua metode penting dalam menyelesaikan sistem persamaan linear dua variabel. Kedua metode ini tidak hanya berguna dalam konteks matematika, tetapi juga memiliki aplikasi yang luas dalam berbagai bidang kehidupan sehari-hari.
Penerapan Metode Substitusi dan Eliminasi dalam Ekonomi
Metode substitusi dan eliminasi dapat digunakan untuk menyelesaikan masalah ekonomi seperti analisis pasar, penentuan harga optimal, dan perencanaan produksi. Sebagai contoh, dalam analisis pasar, metode substitusi dapat digunakan untuk menentukan titik keseimbangan pasar, yaitu titik di mana jumlah barang yang diminta sama dengan jumlah barang yang ditawarkan. Metode eliminasi dapat digunakan untuk menentukan harga optimal suatu produk dengan mempertimbangkan biaya produksi dan permintaan pasar.
Penerapan Metode Substitusi dan Eliminasi dalam Sains
Dalam bidang sains, metode substitusi dan eliminasi dapat digunakan untuk menyelesaikan masalah dalam fisika, kimia, dan biologi. Sebagai contoh, dalam fisika, metode substitusi dapat digunakan untuk menentukan kecepatan dan percepatan suatu objek yang bergerak. Metode eliminasi dapat digunakan untuk menentukan jumlah zat yang bereaksi dalam reaksi kimia.
Penerapan Metode Substitusi dan Eliminasi dalam Teknologi
Metode substitusi dan eliminasi juga memiliki aplikasi yang luas dalam teknologi, khususnya dalam bidang pemrograman, robotika, dan desain sistem. Sebagai contoh, dalam pemrograman, metode substitusi dapat digunakan untuk menentukan nilai variabel dalam program. Metode eliminasi dapat digunakan untuk menentukan nilai optimal parameter dalam sistem robotika.
Contoh Soal Cerita
Seorang tukang kebun ingin mencampur dua jenis pupuk untuk tanamannya. Pupuk A mengandung 10% nitrogen dan 5% fosfor, sedangkan pupuk B mengandung 5% nitrogen dan 10% fosfor. Tukang kebun ingin mendapatkan campuran pupuk yang mengandung 7% nitrogen dan 7% fosfor. Berapa banyak masing-masing pupuk yang harus dicampur?
Untuk menyelesaikan masalah ini, kita dapat menggunakan metode substitusi atau eliminasi. Misalkan x adalah jumlah pupuk A dan y adalah jumlah pupuk B yang dibutuhkan. Kita dapat membuat dua persamaan berdasarkan persentase nitrogen dan fosfor:
* Persamaan Nitrogen: 0.1x + 0.05y = 0.07(x + y)
* Persamaan Fosfor: 0.05x + 0.1y = 0.07(x + y)
Kita dapat menyelesaikan sistem persamaan ini dengan metode substitusi atau eliminasi untuk menentukan nilai x dan y, yang mewakili jumlah pupuk A dan B yang dibutuhkan untuk mendapatkan campuran pupuk yang diinginkan.
Perbedaan Metode Substitusi dan Eliminasi
Dalam matematika, sistem persamaan linear dua variabel sering kali muncul dalam berbagai bidang, mulai dari masalah sehari-hari hingga aplikasi yang lebih kompleks dalam ilmu pengetahuan dan teknik. Untuk menyelesaikan sistem persamaan ini, kita dapat menggunakan berbagai metode, salah satunya adalah metode substitusi dan eliminasi. Kedua metode ini memiliki prinsip yang berbeda, namun sama-sama efektif dalam mencari solusi sistem persamaan linear dua variabel.
Perbedaan Metode Substitusi dan Eliminasi
Metode substitusi dan eliminasi merupakan dua teknik yang berbeda dalam menyelesaikan sistem persamaan linear dua variabel. Perbedaan mendasar antara kedua metode ini terletak pada cara mereka memanipulasi persamaan untuk menemukan solusi.
- Metode substitusi bekerja dengan mengisolasi satu variabel dalam salah satu persamaan dan kemudian mengganti variabel tersebut ke persamaan lainnya.
- Metode eliminasi, di sisi lain, berusaha untuk menghilangkan salah satu variabel dengan menambahkan atau mengurangi kedua persamaan setelah dikalikan dengan faktor tertentu.
Contoh Soal yang Dapat Diselesaikan dengan Kedua Metode
Berikut contoh soal yang dapat diselesaikan dengan kedua metode:
Selesaikan sistem persamaan linear berikut:
x + 2y = 5
2x – y = 1
Metode Substitusi:
- Isolasi variabel x dari persamaan pertama: x = 5 – 2y
- Substitusikan nilai x ke persamaan kedua: 2(5 – 2y) – y = 1
- Selesaikan persamaan untuk y: 10 – 4y – y = 1, 9 = 5y, y = 9/5
- Substitusikan nilai y kembali ke persamaan pertama: x + 2(9/5) = 5, x = 5 – 18/5, x = 7/5
- Solusi sistem persamaan adalah (x, y) = (7/5, 9/5)
Metode Eliminasi:
- Kalikan persamaan pertama dengan 2: 2x + 4y = 10
- Tambahkan persamaan kedua ke persamaan yang telah dikalikan: 2x + 4y + 2x – y = 10 + 1, 4x + 3y = 11
- Kalikan persamaan kedua dengan 4: 8x – 4y = 4
- Tambahkan persamaan yang telah dikalikan dengan persamaan pertama: 8x – 4y + x + 2y = 4 + 5, 9x – 2y = 9
- Selesaikan sistem persamaan baru: 4x + 3y = 11 dan 9x – 2y = 9
- Kalikan persamaan pertama dengan 2 dan persamaan kedua dengan 3: 8x + 6y = 22 dan 27x – 6y = 27
- Tambahkan kedua persamaan: 8x + 6y + 27x – 6y = 22 + 27, 35x = 49, x = 7/5
- Substitusikan nilai x kembali ke persamaan pertama: 7/5 + 2y = 5, 2y = 18/5, y = 9/5
- Solusi sistem persamaan adalah (x, y) = (7/5, 9/5)
Dalam contoh ini, kedua metode memberikan solusi yang sama. Namun, metode substitusi mungkin lebih mudah dalam kasus ini karena kita dapat dengan mudah mengisolasi variabel x dalam persamaan pertama.
Contoh Soal yang Hanya Dapat Diselesaikan dengan Salah Satu Metode
Berikut contoh soal yang hanya dapat diselesaikan dengan metode eliminasi:
Selesaikan sistem persamaan linear berikut:
2x + 3y = 7
4x + 6y = 14
Metode substitusi tidak dapat digunakan dalam kasus ini karena tidak ada variabel yang dapat diisolasi dengan mudah. Namun, metode eliminasi dapat diterapkan dengan mengalikan persamaan pertama dengan -2 dan menambahkannya ke persamaan kedua. Hasilnya adalah 0 = 0, yang menunjukkan bahwa kedua persamaan adalah dependent dan memiliki solusi yang tak terhingga.
Kelebihan dan Kekurangan Metode Substitusi dan Eliminasi
Metode substitusi dan eliminasi adalah dua teknik yang umum digunakan dalam menyelesaikan sistem persamaan linear dua variabel. Masing-masing metode memiliki kelebihan dan kekurangan tersendiri, yang membuat pilihan metode yang tepat bergantung pada jenis soal dan kondisi yang dihadapi.
Kelebihan dan Kekurangan Metode Substitusi
Metode substitusi melibatkan penggantian salah satu variabel dalam persamaan dengan ekspresi yang diperoleh dari persamaan lainnya. Metode ini memiliki kelebihan dan kekurangan sebagai berikut:
- Kelebihan:
- Relatif mudah diterapkan, terutama jika salah satu variabel memiliki koefisien 1 atau -1, sehingga memudahkan isolasi variabel.
- Cocok untuk menyelesaikan sistem persamaan dengan variabel yang sudah diisolasi atau mudah diisolasi.
- Kekurangan:
- Dapat menjadi rumit jika persamaan melibatkan koefisien pecahan atau desimal, karena manipulasi aljabar yang diperlukan bisa lebih kompleks.
- Tidak selalu efektif jika kedua persamaan memiliki koefisien yang sama atau hampir sama, karena proses substitusi dapat menghasilkan persamaan yang kompleks.
Kelebihan dan Kekurangan Metode Eliminasi
Metode eliminasi berfokus pada eliminasi salah satu variabel dengan menggabungkan kedua persamaan. Metode ini juga memiliki kelebihan dan kekurangan:
- Kelebihan:
- Efisien dalam menyelesaikan sistem persamaan dengan koefisien yang sama atau hampir sama, karena eliminasi variabel dapat dilakukan dengan mudah.
- Meminimalkan manipulasi aljabar yang kompleks, sehingga lebih mudah diterapkan untuk persamaan dengan koefisien pecahan atau desimal.
- Kekurangan:
- Membutuhkan penyesuaian koefisien variabel yang akan dieliminasi, yang dapat melibatkan perkalian persamaan dengan konstanta.
- Dapat menjadi rumit jika koefisien variabel tidak mudah disamakan atau melibatkan pecahan dan desimal yang kompleks.
Memilih Metode yang Tepat
Pilihan metode yang tepat untuk menyelesaikan sistem persamaan linear dua variabel tergantung pada jenis soal dan kondisi yang ada. Berikut beberapa pertimbangan:
- Jika salah satu variabel memiliki koefisien 1 atau -1, metode substitusi umumnya lebih mudah diterapkan.
- Jika koefisien variabel sama atau hampir sama, metode eliminasi lebih efisien.
- Jika persamaan melibatkan pecahan atau desimal yang kompleks, metode eliminasi mungkin lebih mudah untuk diimplementasikan.
- Jika salah satu variabel sudah diisolasi, metode substitusi adalah pilihan yang paling langsung.
Soal Latihan Substitusi dan Eliminasi
Metode substitusi dan eliminasi merupakan teknik yang umum digunakan untuk menyelesaikan sistem persamaan linear dua variabel. Kedua metode ini memiliki keunggulan dan kekurangan masing-masing, dan pemilihan metode yang tepat tergantung pada bentuk persamaan yang diberikan.
Soal Latihan Substitusi
Berikut adalah 5 soal latihan tentang sistem persamaan linear dua variabel yang dapat diselesaikan dengan metode substitusi.
Contoh soal substitusi dan eliminasi pada umumnya membahas sistem persamaan linear. Misalnya, mencari nilai x dan y dalam persamaan 2x + y = 5 dan x – y = 1. Nah, setelah mempelajari metode substitusi dan eliminasi, kamu bisa lanjut ke materi statistika seperti menghitung simpangan baku.
Ingin belajar lebih lanjut tentang cara menghitung simpangan baku? Kamu bisa cek contoh soal simpangan baku di link ini. Setelah memahami simpangan baku, kamu bisa kembali ke contoh soal substitusi dan eliminasi dan coba selesaikan dengan lebih mudah!
-
x + 2y = 5
3x – y = 1Penyelesaian:
Dari persamaan pertama, kita peroleh x = 5 – 2y. Substitusikan nilai x ini ke persamaan kedua, sehingga diperoleh:
3(5 – 2y) – y = 1
15 – 6y – y = 1
-7y = -14
y = 2
Substitusikan nilai y = 2 ke persamaan pertama, sehingga diperoleh:
x + 2(2) = 5
x + 4 = 5
x = 1
Jadi, solusi dari sistem persamaan tersebut adalah x = 1 dan y = 2.
-
2x – 3y = 7
x + 4y = 1 -
5x + y = 11
2x – 3y = -5 -
4x – 2y = 10
x + 3y = 1 -
3x + 5y = 2
x – 2y = 1
Soal Latihan Eliminasi
Berikut adalah 5 soal latihan tentang sistem persamaan linear dua variabel yang dapat diselesaikan dengan metode eliminasi.
-
2x + 3y = 11
x – 2y = -1Penyelesaian:
Kalikan persamaan kedua dengan 2, sehingga diperoleh:
2x – 4y = -2
Kurangkan persamaan ini dengan persamaan pertama, sehingga diperoleh:
7y = 13
y = 13/7
Substitusikan nilai y = 13/7 ke persamaan pertama, sehingga diperoleh:
2x + 3(13/7) = 11
2x + 39/7 = 11
2x = 48/7
x = 24/7
Jadi, solusi dari sistem persamaan tersebut adalah x = 24/7 dan y = 13/7.
-
3x + 4y = 10
2x – y = 5 -
5x – 2y = 1
3x + 4y = 17 -
x + 5y = 12
2x – 3y = -1 -
4x + 3y = 19
2x – y = 5
Pembahasan Soal Latihan
Pada bagian ini, kita akan membahas secara detail langkah-langkah penyelesaian untuk setiap soal latihan yang telah diberikan sebelumnya. Pembahasan ini bertujuan untuk memperkuat pemahaman Anda tentang metode substitusi dan eliminasi dalam menyelesaikan sistem persamaan linear.
Soal 1
Soal pertama membahas tentang menentukan nilai x dan y dari sistem persamaan linear berikut:
x + 2y = 5
2x – y = 1
Untuk menyelesaikan soal ini, kita dapat menggunakan metode substitusi. Langkah-langkahnya adalah sebagai berikut:
- Pilih salah satu persamaan dan ubah menjadi bentuk y = … atau x = … . Misalnya, kita pilih persamaan pertama (x + 2y = 5) dan ubah menjadi x = 5 – 2y.
- Substitusikan nilai x yang diperoleh ke persamaan kedua (2x – y = 1). Maka, kita dapatkan 2(5 – 2y) – y = 1.
- Selesaikan persamaan tersebut untuk mencari nilai y. 10 – 4y – y = 1, sehingga -5y = -9 dan y = 9/5.
- Substitusikan nilai y = 9/5 ke persamaan x = 5 – 2y untuk mendapatkan nilai x. x = 5 – 2(9/5) = 11/5.
Jadi, solusi dari sistem persamaan linear tersebut adalah x = 11/5 dan y = 9/5.
Ilustrasi gambar:
Gambar menunjukkan dua garis yang saling berpotongan. Titik potong kedua garis tersebut merupakan solusi dari sistem persamaan linear. Titik potong tersebut terletak pada koordinat (11/5, 9/5).
Soal 2
Soal kedua membahas tentang menentukan nilai x dan y dari sistem persamaan linear berikut:
3x + 4y = 10
2x – 3y = -1
Untuk menyelesaikan soal ini, kita dapat menggunakan metode eliminasi. Langkah-langkahnya adalah sebagai berikut:
- Kalikan kedua persamaan dengan faktor yang tepat sehingga koefisien salah satu variabel sama. Misalnya, kita kalikan persamaan pertama dengan 3 dan persamaan kedua dengan 4. Maka, kita dapatkan:
- 9x + 12y = 30
- 8x – 12y = -4
- Eliminasi variabel y dengan menjumlahkan kedua persamaan. 9x + 8x = 30 – 4, sehingga 17x = 26 dan x = 26/17.
- Substitusikan nilai x = 26/17 ke salah satu persamaan awal untuk mendapatkan nilai y. Misalnya, kita substitusikan ke persamaan pertama (3x + 4y = 10). 3(26/17) + 4y = 10, sehingga 4y = 10 – 78/17 = 92/17 dan y = 23/17.
Jadi, solusi dari sistem persamaan linear tersebut adalah x = 26/17 dan y = 23/17.
Ilustrasi gambar:
Gambar menunjukkan dua garis yang saling berpotongan. Titik potong kedua garis tersebut merupakan solusi dari sistem persamaan linear. Titik potong tersebut terletak pada koordinat (26/17, 23/17).
Soal 3
Soal ketiga membahas tentang menentukan nilai x dan y dari sistem persamaan linear berikut:
x – 3y = 7
2x + y = 1
Untuk menyelesaikan soal ini, kita dapat menggunakan metode eliminasi. Langkah-langkahnya adalah sebagai berikut:
- Kalikan persamaan kedua dengan 3. Maka, kita dapatkan:
- x – 3y = 7
- 6x + 3y = 3
- Eliminasi variabel y dengan menjumlahkan kedua persamaan. x + 6x = 7 + 3, sehingga 7x = 10 dan x = 10/7.
- Substitusikan nilai x = 10/7 ke salah satu persamaan awal untuk mendapatkan nilai y. Misalnya, kita substitusikan ke persamaan pertama (x – 3y = 7). 10/7 – 3y = 7, sehingga -3y = 7 – 10/7 = 39/7 dan y = -13/7.
Jadi, solusi dari sistem persamaan linear tersebut adalah x = 10/7 dan y = -13/7.
Ilustrasi gambar:
Gambar menunjukkan dua garis yang saling berpotongan. Titik potong kedua garis tersebut merupakan solusi dari sistem persamaan linear. Titik potong tersebut terletak pada koordinat (10/7, -13/7).
Referensi dan Sumber Pembelajaran
Metode substitusi dan eliminasi adalah teknik yang penting dalam menyelesaikan sistem persamaan linear. Untuk mempelajari lebih lanjut tentang metode ini, terdapat berbagai sumber pembelajaran yang dapat diakses.
Buku Teks Matematika
Buku teks matematika yang membahas aljabar linear atau persamaan linear biasanya mencakup metode substitusi dan eliminasi. Buku-buku ini menyediakan penjelasan yang komprehensif, contoh soal, dan latihan yang dapat membantu dalam memahami dan menguasai metode ini.
- “Algebra and Trigonometry” oleh Ron Larson dan Robert Hostetler: Buku ini mencakup materi aljabar linear, termasuk metode substitusi dan eliminasi, dengan penjelasan yang mudah dipahami dan banyak contoh soal.
- “Elementary Linear Algebra” oleh Howard Anton dan Chris Rorres: Buku ini memberikan pendekatan yang lebih mendalam pada aljabar linear, dengan fokus pada metode substitusi dan eliminasi dalam menyelesaikan sistem persamaan linear.
Sumber Online
Sumber online seperti situs web dan video pembelajaran dapat memberikan akses mudah dan fleksibel untuk mempelajari metode substitusi dan eliminasi.
- Khan Academy: Platform pembelajaran online ini menyediakan video pembelajaran dan latihan soal yang komprehensif untuk metode substitusi dan eliminasi, dengan penjelasan yang jelas dan mudah dipahami.
- MathPapa: Situs web ini menawarkan kalkulator online yang dapat membantu dalam menyelesaikan sistem persamaan linear menggunakan metode substitusi dan eliminasi, serta menyediakan langkah-langkah penyelesaian yang terperinci.
Sumber Lainnya
Selain buku teks dan sumber online, sumber pembelajaran lainnya seperti tutorial, artikel, dan forum online dapat membantu dalam mempelajari metode substitusi dan eliminasi.
- Tutorial Matematika: Banyak situs web dan blog menyediakan tutorial yang membahas metode substitusi dan eliminasi secara detail, dengan contoh soal dan langkah-langkah penyelesaian yang mudah diikuti.
- Forum Matematika: Forum online seperti Math Stack Exchange dapat memberikan kesempatan untuk bertanya dan berdiskusi dengan ahli matematika dan siswa lain tentang metode substitusi dan eliminasi.
Penutupan Akhir
Dengan memahami metode substitusi dan eliminasi, Anda akan memiliki senjata ampuh untuk menaklukkan berbagai soal sistem persamaan linear dua variabel. Metode ini bukan hanya sekadar rumus, tetapi juga alat berpikir yang dapat membantu Anda dalam menyelesaikan berbagai masalah matematika dan bahkan masalah di kehidupan nyata.