Contoh soal teorema pythagoras segitiga siku siku – Pernahkah kamu penasaran bagaimana cara menghitung panjang sisi-sisi segitiga siku-siku? Teorema Pythagoras adalah kunci untuk mengungkap rahasia ini! Teorema ini menyatakan bahwa kuadrat sisi miring pada segitiga siku-siku sama dengan jumlah kuadrat sisi-sisi lainnya. Sederhana, bukan? Namun, penerapannya sangat luas, mulai dari menghitung jarak hingga membangun gedung tinggi.
Dalam artikel ini, kita akan menjelajahi dunia Teorema Pythagoras dengan berbagai contoh soal, pembahasan, dan latihan. Kamu akan belajar bagaimana menerapkan rumus ini untuk menyelesaikan masalah-masalah menarik yang melibatkan segitiga siku-siku. Siap untuk melangkah lebih jauh dalam memahami konsep geometri ini?
Pengertian Teorema Pythagoras
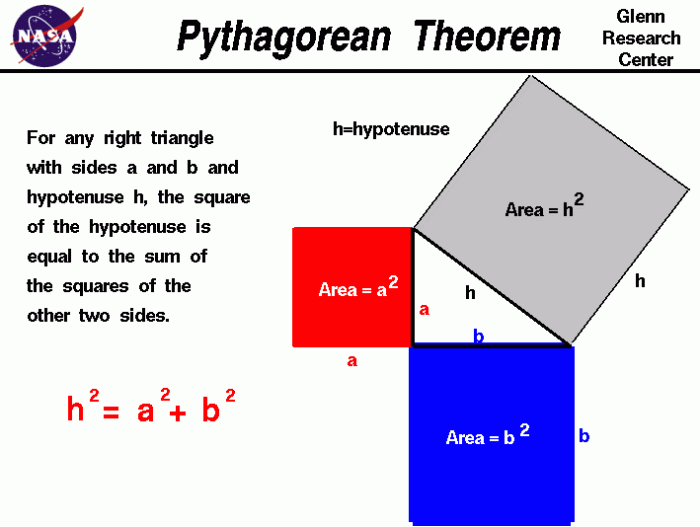
Teorema Pythagoras adalah konsep dasar dalam geometri yang menjelaskan hubungan khusus antara sisi-sisi segitiga siku-siku. Teorema ini menyatakan bahwa kuadrat sisi miring (hipotenusa) sama dengan jumlah kuadrat dari kedua sisi lainnya (sisi tegak).
Ilustrasi Segitiga Siku-Siku
Perhatikan ilustrasi segitiga siku-siku berikut:
Segitiga siku-siku memiliki tiga sisi, yaitu:
- Sisi miring (hipotenusa): Sisi terpanjang dalam segitiga siku-siku, yang berhadapan dengan sudut siku-siku. Dalam ilustrasi, sisi miring dilambangkan dengan huruf c.
- Sisi tegak (alas): Sisi yang berdekatan dengan sudut siku-siku. Dalam ilustrasi, sisi tegak dilambangkan dengan huruf a.
- Sisi tegak (tinggi): Sisi yang berdekatan dengan sudut siku-siku, yang tegak lurus terhadap sisi alas. Dalam ilustrasi, sisi tegak dilambangkan dengan huruf b.
Teorema Pythagoras menyatakan bahwa:
c2 = a2 + b2
Hubungan Sisi-Sisi Segitiga Siku-Siku dan Teorema Pythagoras
Teorema Pythagoras menyatakan bahwa kuadrat sisi miring (c2) sama dengan jumlah kuadrat dari kedua sisi lainnya (a2 + b2). Dengan kata lain, jika Anda mengetahui panjang dua sisi dari segitiga siku-siku, Anda dapat menghitung panjang sisi ketiga menggunakan teorema ini.
Contohnya, jika Anda mengetahui panjang sisi alas (a) dan sisi tinggi (b) dari segitiga siku-siku, Anda dapat menghitung panjang sisi miring (c) dengan menggunakan rumus:
c = √(a2 + b2)
Begitu pula, jika Anda mengetahui panjang sisi miring (c) dan salah satu sisi lainnya (a atau b), Anda dapat menghitung panjang sisi yang belum diketahui dengan menggunakan rumus yang sama.
Rumus Teorema Pythagoras
Teorema Pythagoras merupakan salah satu teorema penting dalam geometri yang berhubungan dengan segitiga siku-siku. Teorema ini menyatakan hubungan antara panjang sisi-sisi segitiga siku-siku. Teorema ini sangat berguna dalam berbagai bidang, seperti arsitektur, teknik, dan fisika.
Rumus Teorema Pythagoras
Rumus Teorema Pythagoras menyatakan bahwa kuadrat sisi miring (hipotenusa) dari sebuah segitiga siku-siku sama dengan jumlah kuadrat dari kedua sisi lainnya (sisi tegak).
a2 + b2 = c2
di mana:
- a adalah panjang sisi tegak pertama
- b adalah panjang sisi tegak kedua
- c adalah panjang sisi miring (hipotenusa)
Contoh Penerapan Rumus Teorema Pythagoras
Misalkan kita memiliki segitiga siku-siku dengan panjang sisi tegak pertama 3 cm dan sisi tegak kedua 4 cm. Kita ingin menghitung panjang sisi miring (hipotenusa).
Dengan menggunakan rumus Teorema Pythagoras, kita dapat menghitung panjang sisi miring:
c2 = a2 + b2
c2 = 32 + 42
c2 = 9 + 16
c2 = 25
c = √25
c = 5 cm
Jadi, panjang sisi miring segitiga siku-siku tersebut adalah 5 cm.
Penerapan Teorema Pythagoras
Teorema Pythagoras memiliki banyak sekali aplikasi dalam kehidupan sehari-hari. Teorema ini memungkinkan kita untuk menghitung panjang sisi-sisi suatu segitiga siku-siku, yang sangat berguna dalam berbagai bidang, mulai dari konstruksi bangunan hingga navigasi.
Contoh Soal Cerita
Misalnya, bayangkan seorang tukang sedang membangun sebuah tangga untuk mencapai atap rumah. Dia ingin mengetahui panjang tangga yang dibutuhkan agar tangga tersebut dapat menjangkau atap dengan aman. Dia tahu bahwa tinggi rumah adalah 5 meter dan jarak kaki tangga ke dinding rumah adalah 12 meter. Dengan menggunakan Teorema Pythagoras, dia dapat menghitung panjang tangga yang dibutuhkan.
Dalam kasus ini, tinggi rumah dan jarak kaki tangga ke dinding rumah merupakan sisi-sisi siku-siku segitiga siku-siku, dan panjang tangga adalah sisi miringnya. Dengan menggunakan rumus Teorema Pythagoras, yaitu a² + b² = c², kita dapat menghitung panjang tangga (c):
c² = 5² + 12²
c² = 25 + 144
c² = 169
c = √169
c = 13 meter
Jadi, panjang tangga yang dibutuhkan adalah 13 meter.
Aplikasi dalam Kehidupan Sehari-hari
- Konstruksi Bangunan: Teorema Pythagoras digunakan dalam berbagai aspek konstruksi bangunan, seperti menghitung panjang diagonal atap, menentukan ukuran balok penyangga, dan memastikan kestabilan struktur bangunan.
- Navigasi: Dalam navigasi, Teorema Pythagoras digunakan untuk menghitung jarak antara dua titik, menentukan arah perjalanan, dan menentukan posisi kapal atau pesawat.
- Seni dan Desain: Teorema Pythagoras juga digunakan dalam seni dan desain, seperti dalam proporsi lukisan, desain furnitur, dan arsitektur bangunan.
Jenis-jenis Soal Teorema Pythagoras: Contoh Soal Teorema Pythagoras Segitiga Siku Siku
Teorema Pythagoras merupakan konsep dasar dalam geometri yang sangat berguna dalam menyelesaikan berbagai masalah yang melibatkan segitiga siku-siku. Teorema ini menyatakan bahwa kuadrat sisi miring (hipotenusa) sama dengan jumlah kuadrat dari kedua sisi lainnya (sisi tegak dan sisi alas). Penerapan teorema ini dapat dijumpai dalam berbagai jenis soal, dan setiap jenis memiliki karakteristik dan pendekatan penyelesaiannya sendiri.
Mencari Panjang Sisi Miring
Salah satu jenis soal Teorema Pythagoras adalah mencari panjang sisi miring (hipotenusa) dari segitiga siku-siku. Dalam kasus ini, kita sudah mengetahui panjang sisi tegak dan sisi alas, dan kita ingin mencari panjang sisi miring. Untuk menyelesaikan soal jenis ini, kita dapat menggunakan rumus Teorema Pythagoras:
c2 = a2 + b2
Dimana:
- c adalah panjang sisi miring (hipotenusa)
- a adalah panjang sisi tegak
- b adalah panjang sisi alas
Untuk menemukan panjang sisi miring, kita dapat mengakar kuadratkan kedua ruas persamaan:
c = √(a2 + b2)
Contoh Soal:
Sebuah segitiga siku-siku memiliki sisi tegak sepanjang 3 cm dan sisi alas sepanjang 4 cm. Berapakah panjang sisi miringnya?
Penyelesaian:
c = √(a2 + b2)
c = √(32 + 42)
c = √(9 + 16)
c = √25
c = 5 cm
Jadi, panjang sisi miring segitiga siku-siku tersebut adalah 5 cm.
Mencari Panjang Sisi Tegak
Jenis soal Teorema Pythagoras lainnya adalah mencari panjang sisi tegak dari segitiga siku-siku. Dalam kasus ini, kita sudah mengetahui panjang sisi miring dan sisi alas, dan kita ingin mencari panjang sisi tegak. Untuk menyelesaikan soal jenis ini, kita dapat menggunakan rumus Teorema Pythagoras yang dimodifikasi:
a2 = c2 – b2
Dimana:
- a adalah panjang sisi tegak
- c adalah panjang sisi miring (hipotenusa)
- b adalah panjang sisi alas
Untuk menemukan panjang sisi tegak, kita dapat mengakar kuadratkan kedua ruas persamaan:
a = √(c2 – b2)
Contoh Soal:
Sebuah segitiga siku-siku memiliki sisi miring sepanjang 10 cm dan sisi alas sepanjang 6 cm. Berapakah panjang sisi tegaknya?
Penyelesaian:
a = √(c2 – b2)
a = √(102 – 62)
a = √(100 – 36)
Contoh soal teorema Pythagoras segitiga siku-siku seringkali melibatkan mencari panjang sisi miring atau salah satu sisi tegak. Misalnya, “Sebuah tangga dengan panjang 5 meter disandarkan ke tembok. Jika jarak kaki tangga ke tembok 3 meter, berapakah tinggi tembok yang dicapai tangga?” Konsep ini juga bisa diterapkan dalam kasus lain, seperti menghitung jarak tempuh pesawat terbang.
Jika ingin mempelajari lebih lanjut mengenai penerapan teorema Pythagoras dalam dunia nyata, kamu bisa melihat contoh soal tabung pitot yang membahas tentang pengukuran kecepatan aliran fluida. Mempelajari berbagai contoh soal seperti ini akan membantu kamu memahami konsep matematika dan penerapannya dalam kehidupan sehari-hari.
a = √64
a = 8 cm
Jadi, panjang sisi tegak segitiga siku-siku tersebut adalah 8 cm.
Mencari Panjang Sisi Alas
Jenis soal Teorema Pythagoras terakhir adalah mencari panjang sisi alas dari segitiga siku-siku. Dalam kasus ini, kita sudah mengetahui panjang sisi miring dan sisi tegak, dan kita ingin mencari panjang sisi alas. Untuk menyelesaikan soal jenis ini, kita dapat menggunakan rumus Teorema Pythagoras yang dimodifikasi:
b2 = c2 – a2
Dimana:
- b adalah panjang sisi alas
- c adalah panjang sisi miring (hipotenusa)
- a adalah panjang sisi tegak
Untuk menemukan panjang sisi alas, kita dapat mengakar kuadratkan kedua ruas persamaan:
b = √(c2 – a2)
Contoh Soal:
Sebuah segitiga siku-siku memiliki sisi miring sepanjang 13 cm dan sisi tegak sepanjang 5 cm. Berapakah panjang sisi alasnya?
Penyelesaian:
b = √(c2 – a2)
b = √(132 – 52)
b = √(169 – 25)
b = √144
b = 12 cm
Jadi, panjang sisi alas segitiga siku-siku tersebut adalah 12 cm.
Contoh Soal dan Pembahasan
Teorema Pythagoras adalah konsep penting dalam geometri yang membantu kita memahami hubungan antara sisi-sisi segitiga siku-siku. Untuk memahami konsep ini lebih dalam, mari kita lihat beberapa contoh soal dan pembahasannya.
Contoh Soal Teorema Pythagoras, Contoh soal teorema pythagoras segitiga siku siku
Berikut adalah beberapa contoh soal Teorema Pythagoras dengan tingkat kesulitan yang berbeda. Setiap soal disertai pembahasan lengkap untuk membantu Anda memahami penerapan rumus Teorema Pythagoras.
| No | Soal | Pembahasan |
|---|---|---|
| 1 | Sebuah segitiga siku-siku memiliki sisi miring sepanjang 10 cm dan salah satu sisi siku-sikunya sepanjang 6 cm. Tentukan panjang sisi siku-siku yang lain! |
Diketahui:
Ditanyakan:
Rumus Teorema Pythagoras:
Substitusikan nilai yang diketahui ke dalam rumus:
Sederhanakan persamaan:
Pindahkan 36 ke ruas kiri:
Hitung selisihnya:
Akar kuadratkan kedua ruas:
Maka, panjang sisi siku-siku yang lain (b) adalah:
|
| 2 | Sebuah tangga bersandar pada tembok dengan sudut 90 derajat. Panjang tangga 5 meter dan jarak kaki tangga ke tembok 3 meter. Tentukan tinggi tembok yang dicapai oleh tangga! |
Diketahui:
Ditanyakan:
Rumus Teorema Pythagoras:
Substitusikan nilai yang diketahui ke dalam rumus:
Sederhanakan persamaan:
Pindahkan 9 ke ruas kiri:
Hitung selisihnya:
Akar kuadratkan kedua ruas:
Maka, tinggi tembok yang dicapai oleh tangga (b) adalah:
|
| 3 | Sebuah taman berbentuk segitiga siku-siku dengan panjang sisi siku-sikunya 12 meter dan 16 meter. Tentukan panjang diagonal taman tersebut! |
Diketahui:
Ditanyakan:
Rumus Teorema Pythagoras:
Substitusikan nilai yang diketahui ke dalam rumus:
Sederhanakan persamaan:
Hitung jumlahnya:
Akar kuadratkan kedua ruas:
Maka, panjang diagonal taman (c) adalah:
|
Latihan Soal
Setelah memahami konsep Teorema Pythagoras, mari kita uji pemahamanmu dengan beberapa soal latihan. Soal-soal ini dirancang dengan berbagai tingkat kesulitan untuk mengasah kemampuanmu dalam menerapkan teorema ini dalam berbagai situasi.
Soal Latihan
Berikut ini adalah 5 soal latihan Teorema Pythagoras dengan berbagai tingkat kesulitan. Soal-soal ini disertai ilustrasi dan petunjuk untuk membantumu dalam menyelesaikannya.
-
Sebuah tangga dengan panjang 10 meter disandarkan ke dinding. Jarak kaki tangga dari dinding adalah 6 meter. Berapakah tinggi dinding yang dicapai tangga?
Petunjuk: Gunakan Teorema Pythagoras untuk mencari tinggi dinding, dengan tangga sebagai sisi miring, jarak kaki tangga dari dinding sebagai alas, dan tinggi dinding sebagai tinggi segitiga siku-siku.
Ilustrasi:
Gambarlah sebuah segitiga siku-siku dengan tangga sebagai sisi miring, jarak kaki tangga dari dinding sebagai alas, dan tinggi dinding sebagai tinggi segitiga.
Kunci Jawaban: Tinggi dinding yang dicapai tangga adalah 8 meter.
-
Sebuah layar televisi memiliki ukuran diagonal 50 inci. Jika lebar layar adalah 40 inci, berapakah tinggi layar tersebut?
Petunjuk: Layar televisi berbentuk persegi panjang, sehingga diagonalnya membagi layar menjadi dua segitiga siku-siku. Gunakan Teorema Pythagoras untuk mencari tinggi layar, dengan diagonal sebagai sisi miring, lebar layar sebagai alas, dan tinggi layar sebagai tinggi segitiga.
Ilustrasi:
Gambarlah sebuah segitiga siku-siku dengan diagonal layar sebagai sisi miring, lebar layar sebagai alas, dan tinggi layar sebagai tinggi segitiga.
Kunci Jawaban: Tinggi layar televisi adalah 30 inci.
-
Sebuah taman berbentuk persegi panjang memiliki panjang 12 meter dan lebar 5 meter. Berapakah panjang diagonal taman tersebut?
Petunjuk: Diagonal taman membagi taman menjadi dua segitiga siku-siku. Gunakan Teorema Pythagoras untuk mencari panjang diagonal, dengan panjang taman sebagai alas, lebar taman sebagai tinggi, dan diagonal sebagai sisi miring.
Ilustrasi:
Gambarlah sebuah segitiga siku-siku dengan panjang taman sebagai alas, lebar taman sebagai tinggi, dan diagonal taman sebagai sisi miring.
Kunci Jawaban: Panjang diagonal taman adalah 13 meter.
-
Sebuah kapal berlayar sejauh 15 km ke arah timur, kemudian berbelok ke arah utara dan berlayar sejauh 20 km. Berapakah jarak terpendek yang harus ditempuh kapal untuk kembali ke titik awal?
Petunjuk: Perjalanan kapal membentuk segitiga siku-siku, dengan jarak ke timur sebagai alas, jarak ke utara sebagai tinggi, dan jarak terpendek untuk kembali ke titik awal sebagai sisi miring. Gunakan Teorema Pythagoras untuk mencari jarak terpendek tersebut.
Ilustrasi:
Gambarlah sebuah segitiga siku-siku dengan jarak ke timur sebagai alas, jarak ke utara sebagai tinggi, dan jarak terpendek untuk kembali ke titik awal sebagai sisi miring.
Kunci Jawaban: Jarak terpendek yang harus ditempuh kapal untuk kembali ke titik awal adalah 25 km.
-
Sebuah layang-layang memiliki panjang diagonal 16 cm dan 12 cm. Berapakah luas layang-layang tersebut?
Petunjuk: Diagonal layang-layang saling tegak lurus dan membagi layang-layang menjadi empat segitiga siku-siku yang kongruen. Gunakan Teorema Pythagoras untuk mencari panjang sisi layang-layang, kemudian hitung luas layang-layang dengan rumus luas layang-layang (1/2 x diagonal 1 x diagonal 2).
Ilustrasi:
Gambarlah sebuah layang-layang dengan kedua diagonalnya. Perhatikan bahwa diagonal layang-layang saling tegak lurus dan membagi layang-layang menjadi empat segitiga siku-siku yang kongruen.
Kunci Jawaban: Luas layang-layang adalah 96 cm2.
Aplikasi Teorema Pythagoras dalam Segitiga Siku-siku
Teorema Pythagoras adalah teorema penting dalam geometri yang menghubungkan sisi-sisi segitiga siku-siku. Teorema ini menyatakan bahwa kuadrat sisi miring (hipotenusa) sama dengan jumlah kuadrat dari kedua sisi lainnya (sisi tegak). Teorema ini memiliki berbagai aplikasi dalam kehidupan nyata, mulai dari konstruksi bangunan hingga navigasi. Dalam konteks segitiga siku-siku, Teorema Pythagoras dapat digunakan untuk berbagai tujuan, seperti menentukan jenis segitiga siku-siku, menghitung panjang sisi, dan menentukan luas segitiga.
Mengenali Jenis Segitiga Siku-siku
Teorema Pythagoras dapat digunakan untuk mengidentifikasi apakah suatu segitiga merupakan segitiga siku-siku atau bukan. Jika kuadrat sisi miring sama dengan jumlah kuadrat kedua sisi lainnya, maka segitiga tersebut adalah segitiga siku-siku. Sebaliknya, jika kuadrat sisi miring tidak sama dengan jumlah kuadrat kedua sisi lainnya, maka segitiga tersebut bukan segitiga siku-siku.
Contoh Soal Identifikasi Segitiga Siku-siku
Misalnya, kita memiliki segitiga dengan panjang sisi 3 cm, 4 cm, dan 5 cm. Untuk menentukan apakah segitiga ini siku-siku, kita dapat menggunakan Teorema Pythagoras. Sisi terpanjang (5 cm) adalah sisi miring, dan dua sisi lainnya (3 cm dan 4 cm) adalah sisi tegak. Kita dapat menghitung kuadrat sisi miring (52 = 25) dan jumlah kuadrat kedua sisi lainnya (32 + 42 = 9 + 16 = 25). Karena kuadrat sisi miring sama dengan jumlah kuadrat kedua sisi lainnya, maka segitiga tersebut adalah segitiga siku-siku.
Menghitung Luas Segitiga Siku-siku
Teorema Pythagoras juga dapat digunakan untuk menghitung luas segitiga siku-siku. Luas segitiga siku-siku dapat dihitung dengan rumus: 1/2 x alas x tinggi. Dalam segitiga siku-siku, alas dan tinggi adalah kedua sisi tegak. Dengan menggunakan Teorema Pythagoras, kita dapat menghitung panjang sisi tegak jika kita mengetahui panjang sisi miring dan salah satu sisi tegak. Dengan mengetahui panjang kedua sisi tegak, kita dapat menghitung luas segitiga siku-siku.
Hubungan Teorema Pythagoras dengan Konsep Geometri Lainnya
Teorema Pythagoras, yang menyatakan bahwa kuadrat sisi miring segitiga siku-siku sama dengan jumlah kuadrat sisi-sisi lainnya, memiliki hubungan erat dengan berbagai konsep geometri lainnya, terutama luas dan keliling segitiga siku-siku serta konsep trigonometri.
Hubungan Teorema Pythagoras dengan Luas dan Keliling Segitiga Siku-Siku
Teorema Pythagoras dapat digunakan untuk menghitung luas dan keliling segitiga siku-siku. Luas segitiga siku-siku dihitung dengan rumus ½ x alas x tinggi, di mana alas dan tinggi adalah sisi-sisi yang membentuk sudut siku-siku. Dengan menggunakan Teorema Pythagoras, kita dapat menghitung panjang alas atau tinggi jika salah satu sisi dan sisi miring diketahui. Keliling segitiga siku-siku adalah jumlah panjang ketiga sisinya. Dengan Teorema Pythagoras, kita dapat menghitung panjang sisi miring jika panjang alas dan tinggi diketahui.
Contoh Soal
Misalnya, sebuah segitiga siku-siku memiliki alas sepanjang 6 cm dan tinggi 8 cm. Untuk menghitung luasnya, kita dapat menggunakan rumus ½ x alas x tinggi, yaitu ½ x 6 cm x 8 cm = 24 cm2. Untuk menghitung kelilingnya, kita perlu menghitung panjang sisi miring terlebih dahulu menggunakan Teorema Pythagoras:
sisi miring2 = alas2 + tinggi2
sisi miring2 = 62 + 82
sisi miring2 = 36 + 64
sisi miring2 = 100
sisi miring = √100 = 10 cm
Keliling segitiga siku-siku adalah 6 cm + 8 cm + 10 cm = 24 cm.
Hubungan Teorema Pythagoras dengan Konsep Trigonometri
Teorema Pythagoras juga memiliki hubungan erat dengan konsep trigonometri. Trigonometri mempelajari hubungan antara sudut dan sisi-sisi segitiga. Dalam segitiga siku-siku, rasio antara panjang sisi-sisi yang berhadapan dengan sudut tertentu disebut dengan fungsi trigonometri, seperti sinus, cosinus, dan tangen. Teorema Pythagoras dapat digunakan untuk menentukan nilai fungsi trigonometri dalam segitiga siku-siku.
Misalnya, jika diketahui panjang sisi miring dan salah satu sisi lainnya, kita dapat menggunakan Teorema Pythagoras untuk menghitung panjang sisi yang tersisa. Dengan mengetahui panjang ketiga sisi, kita dapat menghitung nilai sinus, cosinus, dan tangen dari sudut-sudut dalam segitiga siku-siku.
Kesulitan dalam Mengerjakan Soal Teorema Pythagoras
Teorema Pythagoras adalah konsep fundamental dalam geometri yang menjelaskan hubungan antara sisi-sisi segitiga siku-siku. Meskipun konsepnya sederhana, banyak siswa menghadapi kesulitan dalam mengerjakan soal-soal yang melibatkan Teorema Pythagoras. Kesulitan ini bisa muncul dari berbagai faktor, seperti kurang memahami konsep dasar, kesulitan dalam mengidentifikasi sisi-sisi segitiga, atau kesalahan dalam menghitung.
Kesulitan Umum dalam Mengerjakan Soal Teorema Pythagoras
Berikut adalah beberapa kesulitan umum yang dihadapi siswa dalam mengerjakan soal Teorema Pythagoras:
- Kesulitan dalam mengidentifikasi sisi miring (hipotenusa) dari segitiga siku-siku.
- Kesulitan dalam menentukan sisi yang berhadapan dengan sudut siku-siku.
- Kesulitan dalam menerapkan rumus Teorema Pythagoras dengan benar.
- Kesulitan dalam menyelesaikan persamaan kuadrat yang dihasilkan dari penerapan rumus Teorema Pythagoras.
Contoh Soal yang Sering Menimbulkan Kesulitan
Misalnya, perhatikan soal berikut:
Sebuah tangga dengan panjang 10 meter disandarkan ke dinding. Jika jarak kaki tangga dari dinding adalah 6 meter, berapakah tinggi dinding yang dicapai tangga?
Soal ini seringkali menimbulkan kesulitan karena siswa harus mampu mengidentifikasi sisi-sisi segitiga siku-siku yang terbentuk, yaitu tangga sebagai sisi miring, jarak kaki tangga dari dinding sebagai salah satu sisi tegak, dan tinggi dinding sebagai sisi tegak lainnya. Setelah itu, mereka harus menerapkan rumus Teorema Pythagoras dengan benar untuk menghitung tinggi dinding.
Cara Mengatasi Kesulitan
Untuk mengatasi kesulitan dalam mengerjakan soal Teorema Pythagoras, berikut beberapa tips yang bisa dicoba:
- Pahami konsep dasar Teorema Pythagoras dengan baik. Rumus Teorema Pythagoras menyatakan bahwa kuadrat sisi miring (hipotenusa) sama dengan jumlah kuadrat sisi-sisi lainnya. Pastikan Anda memahami hubungan antara sisi-sisi segitiga siku-siku dan bagaimana rumus ini bekerja.
- Latih mengidentifikasi sisi-sisi segitiga siku-siku. Dalam soal, perhatikan dengan cermat sisi mana yang merupakan sisi miring (hipotenusa), sisi yang berhadapan dengan sudut siku-siku, dan sisi lainnya.
- Berlatih mengerjakan soal-soal yang melibatkan Teorema Pythagoras. Semakin banyak Anda berlatih, semakin mahir Anda dalam menerapkan rumus dan menyelesaikan soal-soal yang kompleks.
- Jika Anda kesulitan dalam menyelesaikan persamaan kuadrat yang dihasilkan dari penerapan rumus Teorema Pythagoras, carilah bantuan dari guru atau teman sekelas Anda.
Penerapan Teorema Pythagoras dalam Bidang Lain
Teorema Pythagoras, yang menyatakan bahwa kuadrat sisi miring segitiga siku-siku sama dengan jumlah kuadrat kedua sisi lainnya, memiliki aplikasi luas dalam berbagai bidang. Penerapannya tidak hanya terbatas pada geometri, tetapi juga meluas ke bidang teknik sipil, arsitektur, ilmu komputer, dan banyak lagi.
Teknik Sipil
Teorema Pythagoras sangat penting dalam teknik sipil, terutama dalam perencanaan dan konstruksi bangunan, jembatan, dan infrastruktur lainnya.
- Perhitungan Panjang Diagonal: Dalam konstruksi, teorema Pythagoras digunakan untuk menghitung panjang diagonal struktur, seperti balok atau kolom, yang membantu menentukan kekuatan dan stabilitas struktur.
- Perencanaan Jalan dan Jembatan: Dalam perencanaan jalan dan jembatan, teorema Pythagoras digunakan untuk menghitung jarak dan kemiringan jalan, serta panjang dan lebar jembatan, yang memastikan keamanan dan efisiensi konstruksi.
- Perhitungan Sudut dan Jarak: Teorema Pythagoras juga digunakan dalam perhitungan sudut dan jarak antara titik-titik dalam proyek konstruksi, yang membantu dalam menentukan lokasi dan orientasi struktur.
Arsitektur
Dalam arsitektur, teorema Pythagoras digunakan dalam perencanaan dan desain bangunan, khususnya dalam hal proporsi, bentuk, dan ruang.
- Desain Atap: Teorema Pythagoras digunakan untuk menghitung panjang lereng atap, yang menentukan sudut dan kemiringan atap, serta kekuatan dan stabilitas struktur.
- Desain Tangga: Teorema Pythagoras digunakan untuk menghitung panjang tangga, yang memastikan keamanan dan kenyamanan pengguna, serta memastikan proporsi yang tepat dengan ruangan.
- Desain Interior: Teorema Pythagoras digunakan dalam desain interior untuk menentukan ukuran dan posisi furnitur, serta untuk menghitung jarak dan sudut antara objek-objek dalam ruangan.
Ilmu Komputer
Teorema Pythagoras juga memiliki aplikasi dalam ilmu komputer, khususnya dalam bidang grafis komputer dan pemrosesan gambar.
- Grafis Komputer: Teorema Pythagoras digunakan untuk menghitung jarak antara titik-titik dalam ruang tiga dimensi, yang membantu dalam rendering objek dan adegan 3D.
- Pemrosesan Gambar: Teorema Pythagoras digunakan dalam algoritma pemrosesan gambar untuk menentukan jarak antara piksel, yang membantu dalam pengenalan pola dan segmentasi gambar.
- Kecerdasan Buatan: Teorema Pythagoras digunakan dalam algoritma pembelajaran mesin untuk menghitung jarak antara titik-titik data, yang membantu dalam klasifikasi dan pengelompokan data.
Akhir Kata
Memahami Teorema Pythagoras bukan hanya tentang menghafal rumus, tetapi juga tentang memahami hubungan antara sisi-sisi segitiga siku-siku. Dengan pemahaman yang kuat, kamu dapat mengaplikasikannya dalam berbagai bidang, mulai dari matematika hingga dunia nyata. Jadi, jangan ragu untuk terus berlatih dan mengeksplorasi Teorema Pythagoras lebih dalam!





