Contoh soal tiga dimensi – Bayangkan sebuah kubus, sebuah bola, atau sebuah piramida. Objek-objek tersebut adalah contoh benda-benda tiga dimensi yang kita temui dalam kehidupan sehari-hari. Dalam dunia matematika, kita mempelajari geometri tiga dimensi untuk memahami bentuk, ukuran, dan posisi benda-benda tersebut.
Contoh soal tiga dimensi hadir untuk membantu kita memahami konsep-konsep penting dalam geometri tiga dimensi, seperti volume, luas permukaan, jarak, dan sudut. Soal-soal ini menguji kemampuan kita dalam memvisualisasikan objek tiga dimensi dan menerapkan rumus-rumus yang tepat untuk menyelesaikan masalah.
Pengertian Soal Tiga Dimensi
Soal tiga dimensi merupakan soal matematika yang melibatkan objek-objek yang memiliki tiga dimensi, yaitu panjang, lebar, dan tinggi. Soal-soal ini umumnya melibatkan konsep-konsep geometri ruang, seperti kubus, balok, limas, kerucut, bola, dan bangun ruang lainnya.
Contoh Soal Tiga Dimensi
Berikut ini adalah contoh soal tiga dimensi yang mudah dipahami:
Sebuah kubus memiliki panjang rusuk 5 cm. Berapakah volume kubus tersebut?
Untuk menyelesaikan soal ini, kita dapat menggunakan rumus volume kubus, yaitu:
Volume kubus = rusuk x rusuk x rusuk
Maka, volume kubus tersebut adalah:
Volume kubus = 5 cm x 5 cm x 5 cm = 125 cm3
Perbedaan Soal Dua Dimensi dan Tiga Dimensi
Soal dua dimensi dan tiga dimensi memiliki perbedaan yang mendasar, yaitu:
| Aspek | Soal Dua Dimensi | Soal Tiga Dimensi |
|---|---|---|
| Dimensi | Hanya memiliki panjang dan lebar | Memiliki panjang, lebar, dan tinggi |
| Contoh Objek | Persegi, lingkaran, segitiga | Kubus, balok, limas, kerucut, bola |
| Contoh Soal | Hitung luas persegi dengan sisi 5 cm | Hitung volume kubus dengan rusuk 5 cm |
Rumus dan Konsep dalam Soal Tiga Dimensi
Soal-soal tiga dimensi (3D) dalam matematika seringkali melibatkan rumus-rumus dan konsep-konsep yang penting untuk memahami bentuk, ukuran, dan posisi objek dalam ruang. Untuk menyelesaikan soal-soal ini, perlu pemahaman yang kuat tentang rumus dasar dan konsep-konsep yang terkait dengan geometri tiga dimensi.
Rumus Dasar dalam Soal Tiga Dimensi
Beberapa rumus dasar yang sering digunakan dalam soal tiga dimensi meliputi:
- Volume Kubus: V = s3, dengan s adalah panjang sisi kubus.
- Luas Permukaan Kubus: L = 6s2, dengan s adalah panjang sisi kubus.
- Volume Balok: V = p x l x t, dengan p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
- Luas Permukaan Balok: L = 2(pl + pt + lt), dengan p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
- Volume Prisma: V = Aalas x t, dengan Aalas adalah luas alas prisma dan t adalah tinggi prisma.
- Luas Permukaan Prisma: L = 2Aalas + Aselimut, dengan Aalas adalah luas alas prisma dan Aselimut adalah luas selimut prisma.
- Volume Limas: V = 1/3 x Aalas x t, dengan Aalas adalah luas alas limas dan t adalah tinggi limas.
- Luas Permukaan Limas: L = Aalas + Aselimut, dengan Aalas adalah luas alas limas dan Aselimut adalah luas selimut limas.
- Volume Bola: V = 4/3πr3, dengan r adalah jari-jari bola.
- Luas Permukaan Bola: L = 4πr2, dengan r adalah jari-jari bola.
- Volume Kerucut: V = 1/3πr2t, dengan r adalah jari-jari alas kerucut dan t adalah tinggi kerucut.
- Luas Permukaan Kerucut: L = πr2 + πrs, dengan r adalah jari-jari alas kerucut, t adalah tinggi kerucut, dan s adalah garis pelukis kerucut.
- Volume Tabung: V = πr2t, dengan r adalah jari-jari alas tabung dan t adalah tinggi tabung.
- Luas Permukaan Tabung: L = 2πr2 + 2πrt, dengan r adalah jari-jari alas tabung dan t adalah tinggi tabung.
Konsep Penting dalam Soal Tiga Dimensi
Selain rumus dasar, beberapa konsep penting dalam soal tiga dimensi meliputi:
- Jarak: Konsep jarak dalam tiga dimensi melibatkan penentuan jarak antara dua titik, garis, atau bidang. Rumus jarak antara dua titik dalam ruang adalah:
- Volume: Volume adalah ukuran ruang yang ditempati oleh suatu objek tiga dimensi. Rumus volume bervariasi tergantung pada bentuk objek, seperti kubus, balok, prisma, limas, bola, kerucut, dan tabung.
- Luas Permukaan: Luas permukaan adalah jumlah luas semua permukaan yang membatasi suatu objek tiga dimensi. Rumus luas permukaan bervariasi tergantung pada bentuk objek, seperti kubus, balok, prisma, limas, bola, kerucut, dan tabung.
- Sudut: Sudut dalam tiga dimensi dapat diukur dalam derajat atau radian. Konsep sudut penting dalam menentukan hubungan antara garis, bidang, dan objek dalam ruang.
d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2)
Langkah-Langkah Menyelesaikan Soal Tiga Dimensi
Berikut adalah langkah-langkah umum dalam menyelesaikan soal tiga dimensi:
- Memahami soal: Baca soal dengan cermat dan pahami apa yang ditanyakan. Identifikasi bentuk objek yang terlibat, data yang diberikan, dan apa yang perlu dicari.
- Menggambar diagram: Gambar diagram yang jelas dari objek tiga dimensi yang terlibat dalam soal. Ini membantu untuk memvisualisasikan bentuk, posisi, dan hubungan antar bagian objek.
- Menerapkan rumus yang tepat: Pilih rumus yang sesuai dengan bentuk objek dan konsep yang terlibat dalam soal.
- Mensubstitusikan nilai: Substitusikan nilai-nilai yang diberikan dalam soal ke dalam rumus yang dipilih.
- Menghitung hasil: Hitung hasil dengan menggunakan operasi matematika yang benar.
- Menulis jawaban: Tulis jawaban akhir dengan satuan yang tepat.
Contoh Soal Tiga Dimensi dan Penyelesaiannya
Soal-soal geometri tiga dimensi seringkali melibatkan konsep-konsep seperti jarak, volume, luas permukaan, dan sudut. Pemahaman yang kuat tentang rumus dan prinsip-prinsip geometri tiga dimensi sangat penting untuk menyelesaikan soal-soal ini. Artikel ini akan membahas beberapa contoh soal tiga dimensi yang umum dijumpai, bersama dengan langkah-langkah penyelesaiannya yang sistematis.
Mencari Volume Kubus
Kubus merupakan bangun ruang dengan enam sisi persegi yang kongruen. Untuk mencari volume kubus, kita dapat menggunakan rumus V = s3, di mana s adalah panjang rusuk kubus.
Contoh soal tiga dimensi bisa dijumpai di berbagai bidang, mulai dari matematika hingga kimia. Soal-soal ini seringkali melibatkan visualisasi dan pemahaman tentang bentuk dan posisi objek di ruang tiga dimensi. Salah satu contohnya adalah soal tentang menghitung volume suatu bangun ruang.
Nah, selain soal tiga dimensi, kamu juga bisa menemukan contoh soal polimeri yang menarik, seperti menghitung derajat polimerisasi suatu polimer. Untuk mempelajari lebih lanjut tentang contoh soal polimeri, kamu bisa mengunjungi contoh soal polimeri. Setelah mempelajari contoh soal polimeri, kamu akan lebih mudah memahami konsep polimerisasi dan penerapannya dalam kehidupan sehari-hari.
Kembali ke soal tiga dimensi, mengerti konsep dasar tiga dimensi akan membantumu dalam memahami materi yang lebih kompleks, seperti geometri ruang dan kalkulus.
Sebagai contoh, misalkan kita memiliki sebuah kubus dengan panjang rusuk 5 cm. Untuk mencari volume kubus tersebut, kita dapat menggunakan rumus di atas:
| Langkah | Rumus | Hasil |
|---|---|---|
| 1. Tentukan panjang rusuk kubus. | s = 5 cm | – |
| 2. Substitusikan nilai s ke dalam rumus V = s3. | V = 53 | – |
| 3. Hitung volume kubus. | V = 125 cm3 | V = 125 cm3 |
Menghitung Luas Permukaan Prisma Segitiga
Prisma segitiga adalah bangun ruang yang memiliki dua sisi sejajar berbentuk segitiga dan tiga sisi tegak berbentuk persegi panjang. Untuk mencari luas permukaan prisma segitiga, kita perlu menghitung luas alas dan luas selimutnya.
Misalkan kita memiliki sebuah prisma segitiga dengan alas berbentuk segitiga siku-siku dengan panjang sisi alas 4 cm, tinggi alas 3 cm, dan panjang sisi miring 5 cm. Panjang sisi tegak prisma adalah 6 cm. Berikut langkah-langkah untuk mencari luas permukaan prisma segitiga:
| Langkah | Rumus | Hasil |
|---|---|---|
| 1. Hitung luas alas prisma. | Lalas = 1/2 x alas x tinggi | Lalas = 1/2 x 4 cm x 3 cm = 6 cm2 |
| 2. Hitung luas selimut prisma. | Lselimut = keliling alas x tinggi prisma | Lselimut = (4 cm + 3 cm + 5 cm) x 6 cm = 72 cm2 |
| 3. Hitung luas permukaan prisma. | Lpermukaan = 2 x Lalas + Lselimut | Lpermukaan = 2 x 6 cm2 + 72 cm2 = 84 cm2 |
Menentukan Jarak Dua Titik dalam Ruang Tiga Dimensi
Jarak dua titik dalam ruang tiga dimensi dapat ditentukan menggunakan rumus jarak, yaitu:
d = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
Misalnya, kita ingin menentukan jarak antara titik A (2, 1, 3) dan titik B (5, 4, 1). Berikut langkah-langkahnya:
| Langkah | Rumus | Hasil |
|---|---|---|
| 1. Tentukan koordinat titik A dan titik B. | A (2, 1, 3) dan B (5, 4, 1) | – |
| 2. Substitusikan nilai koordinat ke dalam rumus jarak. | d = √[(5 – 2)2 + (4 – 1)2 + (1 – 3)2] | – |
| 3. Hitung jarak antara titik A dan titik B. | d = √(9 + 9 + 4) = √22 | d = √22 satuan |
Soal Tiga Dimensi dalam Ujian
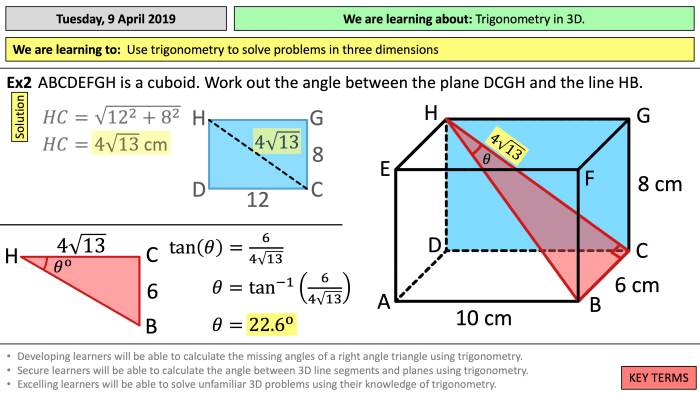
Soal tiga dimensi sering muncul dalam ujian, baik itu ujian nasional maupun ujian masuk perguruan tinggi. Soal ini bertujuan untuk menguji kemampuanmu dalam memahami dan menerapkan konsep geometri ruang, seperti jarak, sudut, volume, dan luas permukaan. Soal-soal ini biasanya disajikan dalam bentuk gambar, diagram, atau model tiga dimensi, yang mengharuskanmu untuk menganalisis dan menginterpretasikan informasi yang diberikan.
Contoh Soal Tiga Dimensi
Berikut adalah beberapa contoh soal tiga dimensi yang sering muncul dalam ujian:
- Hitunglah volume sebuah kubus dengan panjang rusuk 5 cm.
- Sebuah limas segitiga memiliki alas segitiga siku-siku dengan panjang sisi alas 6 cm, 8 cm, dan 10 cm. Jika tinggi limas 12 cm, hitunglah volume limas tersebut.
- Sebuah kerucut memiliki jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah luas permukaan kerucut tersebut.
- Sebuah bola memiliki diameter 14 cm. Hitunglah luas permukaan bola tersebut.
Tips dan Strategi Menyelesaikan Soal Tiga Dimensi
Untuk menyelesaikan soal tiga dimensi dengan baik, berikut beberapa tips dan strategi yang dapat kamu gunakan:
- Pahami Konsep Dasar Geometri Ruang: Sebelum mengerjakan soal, pastikan kamu memahami konsep dasar geometri ruang, seperti rumus volume, luas permukaan, jarak, dan sudut.
- Visualisasikan Soal: Visualisasikan soal dengan baik. Jika soal disajikan dalam bentuk gambar atau diagram, pelajari dengan cermat dan bayangkan bentuk objek yang dimaksud. Jika tidak ada gambar, cobalah untuk menggambar sendiri.
- Identifikasi Informasi yang Diberikan: Identifikasi informasi yang diberikan dalam soal, seperti panjang sisi, jari-jari, tinggi, dan sebagainya. Tuliskan informasi tersebut agar lebih mudah diingat dan dianalisis.
- Gunakan Rumus yang Tepat: Pilih rumus yang tepat untuk menyelesaikan soal. Pastikan kamu memahami rumus yang digunakan dan bagaimana cara mengaplikasikannya.
- Perhatikan Satuan: Perhatikan satuan yang digunakan dalam soal. Pastikan semua satuan sama agar perhitunganmu akurat.
- Latihan Soal Secara Teratur: Latihan soal secara teratur dapat membantumu memahami konsep tiga dimensi dengan lebih baik dan meningkatkan kemampuanmu dalam menyelesaikan soal.
Simpulan Akhir: Contoh Soal Tiga Dimensi
Memahami soal tiga dimensi tidak hanya penting dalam konteks matematika, tetapi juga dalam berbagai bidang seperti arsitektur, teknik, dan desain. Kemampuan kita dalam memvisualisasikan dan menyelesaikan masalah tiga dimensi akan membantu kita dalam memahami dan membangun dunia di sekitar kita.





