Contoh soal transpose matriks beserta jawabannya – Pernahkah kamu mendengar istilah transpose matriks? Transpose matriks adalah konsep dasar dalam aljabar linear yang berperan penting dalam berbagai bidang, seperti analisis data, pemrosesan gambar, dan kriptografi. Dalam artikel ini, kita akan menjelajahi dunia transpose matriks dengan contoh soal dan jawabannya yang mudah dipahami.
Kamu akan mempelajari definisi transpose matriks, cara menentukannya, sifat-sifatnya, dan contoh penerapannya dalam kehidupan nyata. Siap untuk menjelajahi dunia matriks yang menarik? Mari kita mulai!
Cara Menentukan Transpose Matriks
Transpose matriks adalah operasi yang mengubah baris menjadi kolom dan kolom menjadi baris pada matriks. Operasi ini menghasilkan matriks baru yang disebut matriks transpose. Transpose matriks memiliki banyak aplikasi dalam aljabar linear, termasuk dalam penyelesaian sistem persamaan linear dan operasi matriks lainnya.
Langkah-Langkah Menentukan Transpose Matriks
Menentukan transpose matriks cukup mudah, berikut langkah-langkahnya:
- Tukar baris dan kolom pada matriks awal.
- Elemen pada baris ke-i dan kolom ke-j pada matriks awal akan menjadi elemen pada kolom ke-i dan baris ke-j pada matriks transpose.
Contoh Soal Transpose Matriks
Misalnya, kita memiliki matriks 2×2 berikut:
A =
[1 2]
[3 4]
Langkah-langkah menentukan transpose matriks A adalah:
- Tentukan dimensi matriks A. Matriks A memiliki 2 baris dan 2 kolom, sehingga dimensi matriks A adalah 2×2.
- Buat matriks transpose A dengan dimensi yang terbalik, yaitu 2×2.
- Tukar baris dan kolom matriks A. Elemen pada baris pertama kolom pertama (1) menjadi elemen pada kolom pertama baris pertama, elemen pada baris pertama kolom kedua (2) menjadi elemen pada kolom kedua baris pertama, dan seterusnya.
Hasil transpose matriks A adalah:
AT =
[1 3]
[2 4]
Tabel Langkah Menentukan Transpose Matriks
Berikut tabel yang menunjukkan langkah-langkah menentukan transpose matriks:
| Langkah | Penjelasan |
|---|---|
| 1. Tentukan dimensi matriks awal. | Tentukan jumlah baris dan kolom pada matriks awal. |
| 2. Buat matriks transpose dengan dimensi terbalik. | Jika matriks awal berdimensi mxn, maka matriks transpose berdimensi nxm. |
| 3. Tukar baris dan kolom pada matriks awal. | Elemen pada baris ke-i dan kolom ke-j pada matriks awal akan menjadi elemen pada kolom ke-i dan baris ke-j pada matriks transpose. |
Sifat-sifat Transpose Matriks
Setelah mempelajari cara menentukan transpose matriks, sekarang saatnya kita bahas sifat-sifat menarik yang dimiliki operasi transpose ini. Sifat-sifat ini akan membantu kita dalam memahami dan menyelesaikan berbagai operasi matriks yang melibatkan transpose.
Transpose dari Transpose Matriks
Sifat pertama yang akan kita bahas adalah transpose dari transpose matriks. Singkatnya, jika kita mentransposekan sebuah matriks dua kali, hasilnya adalah matriks awal itu sendiri.
(AT)T = A
Contohnya, jika kita memiliki matriks A:
A =
[1 2]
[3 4]
Transpose dari A adalah:
AT =
[1 3]
[2 4]
Dan transpose dari AT adalah:
(AT)T =
[1 2]
[3 4]
Ngomongin soal matriks, pasti kamu pernah denger transpose kan? Nah, buat ngelatih pemahaman tentang transpose matriks, banyak banget contoh soal beserta jawabannya yang bisa kamu temuin di internet. Tapi, selain transpose matriks, kamu juga perlu belajar tentang statistik deskriptif, yang bisa kamu pelajari lebih lanjut dengan klik contoh soal statistik deskriptif ini.
Nah, setelah memahami konsep transpose matriks dan statistik deskriptif, kamu bisa mencoba menjawab soal-soal latihan untuk menguji kemampuanmu.
Seperti yang kita lihat, hasil transpose dari transpose matriks A adalah matriks A itu sendiri.
Transpose dari Penjumlahan Matriks
Sifat selanjutnya adalah transpose dari penjumlahan matriks. Transpose dari penjumlahan dua matriks sama dengan penjumlahan dari transpose masing-masing matriks.
(A + B)T = AT + BT
Misalnya, jika kita memiliki matriks A dan B:
A =
[1 2]
[3 4]
B =
[5 6]
[7 8]
Penjumlahan A dan B adalah:
A + B =
[6 8]
[10 12]
Transpose dari (A + B) adalah:
(A + B)T =
[6 10]
[8 12]
Transpose dari A dan B adalah:
AT =
[1 3]
[2 4]
BT =
[5 7]
[6 8]
Penjumlahan AT dan BT adalah:
AT + BT =
[6 10]
[8 12]
Terbukti bahwa transpose dari penjumlahan A dan B sama dengan penjumlahan dari transpose masing-masing matriks.
Transpose dari Perkalian Matriks
Sifat terakhir yang akan kita bahas adalah transpose dari perkalian matriks. Transpose dari perkalian dua matriks sama dengan perkalian dari transpose masing-masing matriks, tetapi dengan urutan yang dibalik.
(AB)T = BTAT
Contohnya, jika kita memiliki matriks A dan B:
A =
[1 2]
[3 4]
B =
[5 6]
[7 8]
Perkalian A dan B adalah:
AB =
[19 22]
[43 50]
Transpose dari (AB) adalah:
(AB)T =
[19 43]
[22 50]
Transpose dari A dan B adalah:
AT =
[1 3]
[2 4]
BT =
[5 7]
[6 8]
Perkalian BT dan AT adalah:
BTAT =
[19 43]
[22 50]
Terbukti bahwa transpose dari perkalian A dan B sama dengan perkalian dari transpose masing-masing matriks, tetapi dengan urutan yang dibalik.
Tabel Sifat Transpose Matriks
| Sifat | Contoh |
|---|---|
| Transpose dari transpose matriks | (AT)T = A |
| Transpose dari penjumlahan matriks | (A + B)T = AT + BT |
| Transpose dari perkalian matriks | (AB)T = BTAT |
Contoh Soal Transpose Matriks: Contoh Soal Transpose Matriks Beserta Jawabannya
Transpose matriks merupakan operasi matematika yang mengubah baris menjadi kolom dan kolom menjadi baris dalam matriks. Untuk lebih memahami konsep transpose matriks, mari kita lihat beberapa contoh soal berikut.
Contoh Soal 1: Matriks Berordo 2×2
Contoh soal pertama ini menggunakan matriks berordo 2×2. Matriks ini memiliki dua baris dan dua kolom.
Misalkan kita memiliki matriks A:
A =
1 2 3 4
Untuk mendapatkan transpose matriks A, kita perlu menukar posisi baris dan kolomnya.
AT =
1 3 2 4
Jadi, transpose matriks A adalah:
AT =
1 3 2 4
Contoh Soal 2: Matriks Berordo 3×3, Contoh soal transpose matriks beserta jawabannya
Contoh soal kedua ini menggunakan matriks berordo 3×3. Matriks ini memiliki tiga baris dan tiga kolom.
Misalkan kita memiliki matriks B:
B =
1 2 3 4 5 6 7 8 9
Untuk mendapatkan transpose matriks B, kita perlu menukar posisi baris dan kolomnya.
BT =
1 4 7 2 5 8 3 6 9
Jadi, transpose matriks B adalah:
BT =
1 4 7 2 5 8 3 6 9
Contoh Soal 3: Matriks Berordo 2×3
Contoh soal ketiga ini menggunakan matriks berordo 2×3. Matriks ini memiliki dua baris dan tiga kolom.
Misalkan kita memiliki matriks C:
C =
1 2 3 4 5 6
Untuk mendapatkan transpose matriks C, kita perlu menukar posisi baris dan kolomnya.
CT =
1 4 2 5 3 6
Jadi, transpose matriks C adalah:
CT =
1 4 2 5 3 6
Penerapan Transpose Matriks
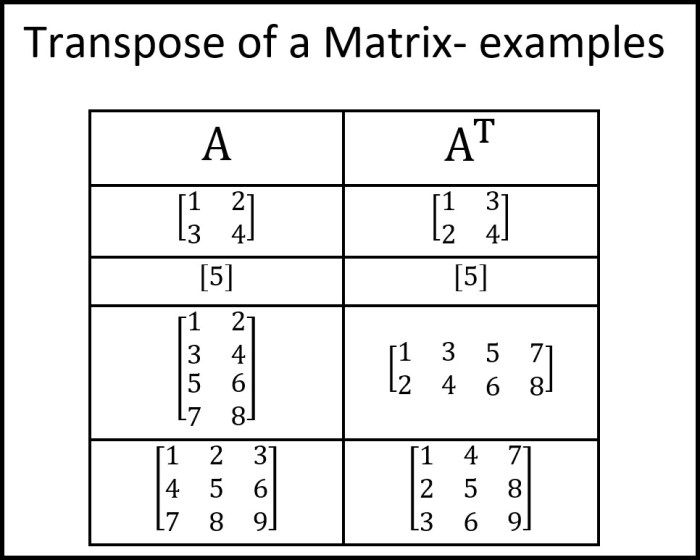
Transpose matriks, selain sebagai operasi matematika dasar, memiliki peran penting dalam berbagai bidang. Penerapannya tidak terbatas pada dunia akademis, tetapi juga merambah ke berbagai aspek kehidupan nyata.
Analisis Data Statistik
Transpose matriks berperan penting dalam analisis data statistik. Data statistik sering kali disusun dalam bentuk tabel atau matriks, di mana baris mewakili variabel dan kolom mewakili observasi. Transpose matriks memungkinkan kita untuk mengubah orientasi data, sehingga memudahkan analisis. Misalnya, dalam tabel yang berisi data penjualan produk di berbagai toko, transpose matriks dapat digunakan untuk mengubah orientasi data sehingga kita dapat melihat penjualan setiap toko untuk semua produk.
Pemrosesan Gambar
Dalam pemrosesan gambar, transpose matriks digunakan untuk mengubah orientasi gambar. Gambar digital disimpan dalam bentuk matriks, di mana setiap elemen matriks mewakili intensitas warna piksel. Transpose matriks dapat digunakan untuk memutar gambar 90 derajat, sehingga mengubah orientasi gambar dari lanskap menjadi potret atau sebaliknya. Misalnya, dalam program pengeditan gambar, transpose matriks digunakan untuk memutar gambar secara vertikal atau horizontal.
Kriptografi
Transpose matriks juga memiliki aplikasi dalam kriptografi, khususnya dalam teknik enkripsi yang dikenal sebagai enkripsi transposisi. Teknik ini bekerja dengan mengacak urutan karakter dalam pesan dengan menggunakan transpose matriks. Misalnya, pesan “RAHASIA” dapat dienkripsi dengan menggunakan matriks transpose untuk mengubah urutan karakter menjadi “ARHSAI”. Penerima pesan kemudian dapat menggunakan matriks transpose yang sama untuk mendekripsi pesan tersebut.
Latihan Soal Transpose Matriks
Transpose matriks merupakan operasi dasar dalam aljabar linear yang mengubah baris menjadi kolom dan kolom menjadi baris. Operasi ini memiliki berbagai aplikasi dalam matematika, statistika, dan ilmu komputer. Untuk memahami konsep transpose matriks dengan lebih baik, mari kita selesaikan beberapa latihan soal.
Latihan Soal Transpose Matriks
Berikut ini adalah 5 soal transpose matriks dengan tingkat kesulitan yang bervariasi, beserta jawabannya:
| Soal | Jawaban |
|---|---|
| Transpose matriks A = [ 1 2 3 ] [ 4 5 6 ] [ 7 8 9 ] |
AT = [ 1 4 7 ] [ 2 5 8 ] [ 3 6 9 ] |
| Transpose matriks B = [ 2 -1 ] [ 3 4 ] |
BT = [ 2 3 ] [ -1 4 ] |
| Transpose matriks C = [ 1 0 -2 ] |
CT = [ 1 ] [ 0 ] [ -2 ] |
| Transpose matriks D = [ 1 ] [ 2 ] [ 3 ] |
DT = [ 1 2 3 ] |
| Transpose matriks E = [ 1 2 3 4 ] [ 5 6 7 8 ] [ 9 10 11 12 ] |
ET = [ 1 5 9 ] [ 2 6 10 ] [ 3 7 11 ] [ 4 8 12 ] |
Ulasan Penutup
Dengan memahami konsep transpose matriks, kamu telah membuka pintu menuju pemahaman yang lebih dalam tentang aljabar linear. Kemampuan untuk menentukan transpose matriks dan memahami sifat-sifatnya akan sangat berguna dalam menyelesaikan berbagai masalah matematika dan aplikasi nyata. Ingatlah bahwa latihan adalah kunci untuk menguasai konsep ini, jadi jangan ragu untuk mencoba berbagai contoh soal transpose matriks dan membangun pemahaman yang kuat.





