Pernahkah Anda bertanya-tanya bagaimana aplikasi navigasi menemukan rute tercepat, atau bagaimana mesin pencari menampilkan hasil yang paling relevan? Di balik keajaiban teknologi ini terdapat algoritma yang cerdas, salah satunya adalah algoritma greedy. Contoh Soal Algoritma Greedy akan mengajak Anda untuk menyelami dunia pemrograman yang menarik ini, dan mempelajari bagaimana algoritma greedy dapat diterapkan dalam berbagai masalah optimasi.
Algoritma greedy merupakan pendekatan yang sederhana namun efektif dalam menyelesaikan masalah dengan memilih pilihan terbaik pada setiap langkah. Dalam konteks pemrograman, algoritma ini bekerja dengan mencari solusi optimal secara bertahap, tanpa perlu melihat kembali keputusan yang telah diambil sebelumnya. Bayangkan Anda sedang memilih buah di pasar, algoritma greedy akan memilih buah yang paling matang dan segar di setiap kesempatan, tanpa mempertimbangkan kemungkinan buah yang lebih baik di kemudian hari.
Pengertian Algoritma Greedy
Algoritma greedy merupakan salah satu strategi dalam pemrograman yang bertujuan untuk menemukan solusi optimal untuk suatu masalah dengan melakukan serangkaian pilihan yang terbaik pada setiap langkahnya, tanpa mempertimbangkan konsekuensi jangka panjang dari pilihan tersebut. Dalam konteks pemrograman, algoritma greedy sering digunakan untuk memecahkan masalah optimasi, di mana tujuannya adalah untuk menemukan solusi terbaik yang memenuhi batasan tertentu.
Contoh Sederhana Algoritma Greedy
Bayangkan kamu sedang berbelanja di supermarket dan ingin membeli sebanyak mungkin barang dengan uang yang terbatas. Kamu akan cenderung memilih barang-barang yang memiliki harga paling murah per unit, karena dengan cara ini kamu bisa mendapatkan lebih banyak barang dengan uang yang sama. Strategi ini, memilih barang termurah per unit pada setiap langkah, merupakan contoh sederhana dari algoritma greedy.
Karakteristik Algoritma Greedy
Algoritma greedy memiliki beberapa karakteristik utama yang membedakannya dari algoritma lainnya. Berikut adalah beberapa karakteristik tersebut:
- Membuat keputusan optimal secara lokal: Algoritma greedy memilih pilihan terbaik pada setiap langkah, tanpa mempertimbangkan dampaknya terhadap langkah-langkah selanjutnya. Ini berarti algoritma greedy dapat menghasilkan solusi yang suboptimal secara global, meskipun optimal secara lokal.
- Serakah: Algoritma greedy selalu memilih pilihan yang paling menguntungkan pada saat itu, tanpa mempertimbangkan konsekuensi jangka panjang. Ini dapat menyebabkan algoritma greedy terjebak dalam solusi lokal yang bukan solusi global terbaik.
- Tidak selalu optimal: Algoritma greedy tidak selalu menghasilkan solusi optimal untuk setiap masalah. Ada banyak kasus di mana algoritma greedy menghasilkan solusi yang suboptimal, terutama untuk masalah yang kompleks.
- Efisien: Algoritma greedy biasanya mudah diterapkan dan efisien secara komputasi, karena tidak perlu mempertimbangkan semua kemungkinan solusi. Ini menjadikannya pilihan yang baik untuk masalah yang membutuhkan solusi cepat.
Prinsip Kerja Algoritma Greedy
Algoritma greedy adalah pendekatan yang bertujuan untuk menemukan solusi optimal dengan memilih pilihan terbaik pada setiap langkah, tanpa melihat dampak jangka panjang dari pilihan tersebut. Dalam konteks ini, “terbaik” biasanya didefinisikan berdasarkan beberapa metrik yang telah ditentukan sebelumnya, seperti memaksimalkan keuntungan atau meminimalkan biaya. Meskipun algoritma greedy tidak selalu menghasilkan solusi optimal global, mereka sering memberikan solusi yang cukup baik dalam waktu yang relatif singkat, terutama untuk masalah yang kompleks.
Contoh soal algoritma greedy seringkali muncul dalam konteks optimasi, seperti mencari solusi terbaik untuk suatu masalah dengan langkah-langkah yang serakah. Salah satu contohnya adalah masalah penjadwalan tugas. Nah, kalau kamu ingin memahami lebih dalam tentang contoh soal geometri, khususnya persegi panjang, bisa cek di contoh soal persegi panjang beserta jawabannya.
Memahami konsep dasar geometri seperti persegi panjang dapat membantu kamu dalam menyelesaikan berbagai macam masalah algoritma, termasuk algoritma greedy.
Cara Algoritma Greedy Membuat Keputusan
Algoritma greedy membuat keputusan berdasarkan prinsip memilih pilihan yang tampak paling menguntungkan pada saat itu, tanpa mempertimbangkan efek jangka panjang dari pilihan tersebut. Pendekatan ini dapat diilustrasikan dengan analogi seorang pendaki gunung yang ingin mencapai puncak gunung dengan cepat. Pada setiap titik, pendaki akan memilih jalur yang tampak paling curam dan mudah diakses, meskipun jalur tersebut mungkin tidak mengarah langsung ke puncak. Meskipun strategi ini mungkin tidak selalu optimal, tetapi seringkali menghasilkan hasil yang cukup baik dalam waktu singkat.
Langkah-Langkah Umum Penerapan Algoritma Greedy
- Tentukan Fungsi Tujuan: Tentukan metrik yang akan dioptimalkan (maksimalkan keuntungan, minimalkan biaya, dll.).
- Definisikan Kriteria Greedy: Tentukan aturan yang digunakan untuk memilih pilihan terbaik pada setiap langkah.
- Inisialisasi Solusi: Mulailah dengan solusi awal yang kosong.
- Iterasi: Secara berulang, pilih pilihan terbaik yang tersedia berdasarkan kriteria greedy dan tambahkan ke solusi.
- Hentikan Iterasi: Hentikan iterasi ketika semua pilihan telah dipertimbangkan atau kriteria berhenti terpenuhi.
Contoh Penerapan Algoritma Greedy: Masalah Penukaran Uang
Bayangkan Anda memiliki mesin penjual otomatis yang hanya menerima uang logam. Anda ingin memberikan kembalian kepada pelanggan dengan jumlah tertentu menggunakan jumlah uang logam yang seminimal mungkin. Algoritma greedy dapat digunakan untuk menyelesaikan masalah ini.
Fungsi Tujuan: Minimalkan jumlah uang logam yang digunakan untuk memberikan kembalian.
Kriteria Greedy: Pilih uang logam dengan nilai terbesar yang tidak melebihi jumlah kembalian yang tersisa.
Contoh: Misalkan Anda perlu memberikan kembalian sebesar Rp. 1.250. Berikut langkah-langkah penerapan algoritma greedy:
- Inisialisasi: Solusi awal kosong.
- Iterasi 1: Nilai uang logam terbesar yang tidak melebihi Rp. 1.250 adalah Rp. 1.000. Tambahkan satu uang logam Rp. 1.000 ke solusi. Sisa kembalian Rp. 250.
- Iterasi 2: Nilai uang logam terbesar yang tidak melebihi Rp. 250 adalah Rp. 200. Tambahkan satu uang logam Rp. 200 ke solusi. Sisa kembalian Rp. 50.
- Iterasi 3: Nilai uang logam terbesar yang tidak melebihi Rp. 50 adalah Rp. 50. Tambahkan satu uang logam Rp. 50 ke solusi. Sisa kembalian Rp. 0.
- Hentikan Iterasi: Sisa kembalian Rp. 0, jadi iterasi berhenti.
Dengan demikian, solusi optimal untuk masalah ini adalah satu uang logam Rp. 1.000, satu uang logam Rp. 200, dan satu uang logam Rp. 50.
Keuntungan dan Kerugian Algoritma Greedy
Setelah mempelajari dasar-dasar algoritma greedy, penting untuk memahami kekuatan dan keterbatasannya. Algoritma greedy, dengan fokusnya pada pilihan optimal di setiap langkah, memiliki beberapa keuntungan dan kerugian yang perlu dipertimbangkan dalam konteks penerapannya.
Keuntungan Algoritma Greedy
Algoritma greedy menawarkan beberapa keuntungan yang membuatnya menarik untuk berbagai aplikasi:
- Kemudahan Implementasi: Algoritma greedy biasanya mudah dipahami dan diimplementasikan. Logika “ambil pilihan terbaik di setiap langkah” membuatnya relatif mudah diterjemahkan ke dalam kode.
- Efisiensi Waktu: Karena algoritma greedy membuat keputusan lokal tanpa mempertimbangkan solusi masa depan, mereka biasanya memiliki kompleksitas waktu yang rendah, menjadikannya pilihan yang baik untuk masalah dengan batasan waktu yang ketat.
- Solusi Praktis: Dalam banyak kasus, algoritma greedy memberikan solusi yang “cukup baik” yang dapat diterima dalam praktik. Meskipun mungkin tidak selalu menghasilkan solusi optimal, mereka seringkali menghasilkan solusi yang cukup dekat dengan optimal.
Kerugian Algoritma Greedy
Meskipun memiliki keuntungan, algoritma greedy juga memiliki kelemahan yang perlu dipertimbangkan:
- Tidak Selalu Optimal: Algoritma greedy tidak selalu menghasilkan solusi optimal. Karena mereka membuat keputusan berdasarkan informasi lokal, mereka dapat kehilangan solusi global yang lebih baik yang mungkin ditemukan dengan mempertimbangkan semua kemungkinan.
- Ketergantungan pada Masalah: Efektivitas algoritma greedy sangat bergantung pada masalah yang sedang dipecahkan. Ada kasus di mana algoritma greedy dapat memberikan solusi yang sangat buruk, sedangkan di kasus lain mereka dapat menghasilkan solusi yang sangat baik.
- Tidak Cocok untuk Semua Masalah: Algoritma greedy tidak cocok untuk semua jenis masalah. Mereka biasanya bekerja dengan baik untuk masalah dengan struktur sederhana dan pilihan lokal yang independen. Namun, untuk masalah yang lebih kompleks dengan interaksi yang kompleks antara pilihan, algoritma greedy mungkin tidak memberikan solusi yang memuaskan.
Perbandingan Algoritma Greedy dengan Algoritma Lainnya
| Karakteristik | Algoritma Greedy | Algoritma Dinamis | Algoritma Divide and Conquer |
|---|---|---|---|
| Kompleksitas Waktu | Biasanya rendah | Bergantung pada masalah, dapat tinggi | Biasanya rendah |
| Optimalitas | Tidak selalu optimal | Biasanya optimal | Biasanya optimal |
| Kemudahan Implementasi | Mudah | Lebih kompleks | Lebih kompleks |
| Fleksibilitas | Kurang fleksibel | Lebih fleksibel | Lebih fleksibel |
| Contoh Aplikasi | Perencanaan rute, algoritma Huffman | Perhitungan jarak terpendek, pengisian ransel | Pencarian biner, pengurutan merge |
Penerapan Algoritma Greedy dalam Masalah Klasik
Algoritma greedy adalah pendekatan yang sederhana dan efektif untuk memecahkan berbagai masalah optimasi. Prinsip utamanya adalah membuat pilihan terbaik di setiap langkah, dengan harapan bahwa serangkaian pilihan terbaik ini akan mengarah pada solusi optimal secara keseluruhan. Meskipun tidak selalu menjamin solusi optimal, algoritma greedy sering kali memberikan hasil yang baik dan dapat diterapkan pada berbagai masalah praktis.
Penerapan Algoritma Greedy dalam Masalah Penjadwalan
Salah satu penerapan algoritma greedy yang umum adalah dalam masalah penjadwalan. Dalam masalah ini, kita memiliki serangkaian tugas dengan durasi tertentu dan batasan waktu, dan tujuannya adalah untuk menjadwalkan tugas-tugas tersebut sedemikian rupa sehingga semua tugas selesai dalam waktu sesingkat mungkin. Misalnya, kita mungkin ingin menjadwalkan presentasi di sebuah konferensi, dengan setiap presentasi memiliki durasi tertentu dan waktu mulai yang diinginkan. Algoritma greedy dapat digunakan untuk menentukan urutan presentasi yang meminimalkan total waktu yang dibutuhkan untuk menyelesaikan semua presentasi.
Salah satu algoritma greedy yang umum digunakan untuk masalah penjadwalan adalah algoritma Shortest Job First (SJF). Algoritma ini memilih tugas dengan durasi terpendek untuk dijadwalkan terlebih dahulu. Ide di balik algoritma ini adalah dengan menyelesaikan tugas-tugas yang lebih pendek terlebih dahulu, kita dapat meminimalkan waktu tunggu untuk tugas-tugas yang lebih panjang. Namun, algoritma SJF tidak selalu menjamin solusi optimal, terutama jika ada batasan waktu yang ketat. Dalam beberapa kasus, mungkin lebih baik untuk menjadwalkan tugas yang memiliki batasan waktu yang ketat terlebih dahulu, meskipun durasinya lebih panjang.
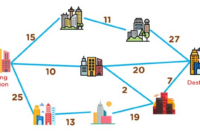
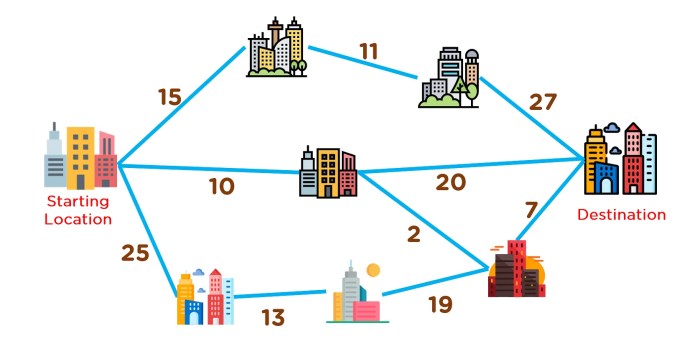
Contoh Soal Algoritma Greedy untuk Masalah Pencarian Jalur Terpendek
Misalnya, kita ingin menemukan jalur terpendek dari titik A ke titik B pada sebuah peta. Kita dapat menggunakan algoritma greedy untuk memilih jalur yang paling pendek di setiap persimpangan. Misalnya, jika kita berada di titik A dan memiliki tiga pilihan jalur, kita akan memilih jalur yang paling pendek ke persimpangan berikutnya. Kita akan terus memilih jalur terpendek di setiap persimpangan sampai mencapai titik B.
Namun, algoritma greedy tidak selalu menjamin jalur terpendek secara keseluruhan. Misalnya, jika kita memiliki dua jalur dari titik A ke titik B, dengan jalur pertama memiliki bagian awal yang lebih panjang tetapi bagian akhir yang lebih pendek, dan jalur kedua memiliki bagian awal yang lebih pendek tetapi bagian akhir yang lebih panjang, algoritma greedy mungkin memilih jalur kedua karena bagian awal yang lebih pendek. Namun, jalur pertama mungkin merupakan jalur terpendek secara keseluruhan. Oleh karena itu, penting untuk mempertimbangkan batasan dan kompleksitas masalah saat menggunakan algoritma greedy.
Masalah Klasik yang Dapat Diselesaikan dengan Algoritma Greedy
| Masalah | Penerapan Algoritma Greedy |
|---|---|
| Pencarian Jalur Terpendek | Algoritma Dijkstra, Algoritma A* |
| Penjadwalan Tugas | Algoritma Shortest Job First (SJF), Algoritma Earliest Deadline First (EDF) |
| Pemilihan Koin | Algoritma Greedy Coin Change |
| Pemilihan Set | Algoritma Greedy Set Cover |
| Huffman Coding | Algoritma Greedy Huffman Coding |
Contoh Soal Algoritma Greedy
Algoritma greedy merupakan strategi yang sering digunakan dalam pemecahan masalah optimasi. Dalam algoritma ini, kita membuat serangkaian keputusan yang tampaknya optimal pada setiap langkah, tanpa mempertimbangkan konsekuensi jangka panjang. Dalam contoh soal berikut, kita akan melihat bagaimana algoritma greedy dapat digunakan untuk menyelesaikan masalah klasik dalam teori graf, yaitu masalah pencarian pohon rentang minimum (Minimum Spanning Tree).
Masalah Pencarian Pohon Rentang Minimum
Bayangkan Anda memiliki sebuah peta yang menunjukkan jaringan jalan di sebuah kota. Anda ingin menemukan cara termudah untuk menghubungkan semua titik penting di kota tersebut dengan jalan terpendek. Masalah ini dapat dimodelkan sebagai graf, di mana titik-titik penting adalah simpul dan jalan adalah sisi. Masalah pencarian pohon rentang minimum adalah menemukan subset dari sisi-sisi graf yang menghubungkan semua simpul dengan total panjang sisi terpendek.
Algoritma Kruskal
Salah satu algoritma greedy yang populer untuk menyelesaikan masalah pencarian pohon rentang minimum adalah algoritma Kruskal. Algoritma ini bekerja dengan memilih sisi terpendek yang tersedia di setiap langkah, dengan syarat sisi tersebut tidak menciptakan siklus. Berikut adalah langkah-langkahnya:
- Urutkan semua sisi dalam graf berdasarkan panjangnya, dari yang terpendek ke yang terpanjang.
- Mulailah dengan set sisi kosong.
- Untuk setiap sisi dalam urutan yang diurutkan:
- Jika sisi tersebut tidak menciptakan siklus dalam set sisi yang ada, tambahkan sisi tersebut ke set sisi.
- Ulangi langkah 3 sampai semua simpul terhubung.
Contoh Penerapan
Mari kita lihat contoh penerapan algoritma Kruskal. Misalkan kita memiliki graf berikut:
| Sisi | Panjang |
|---|---|
| AB | 1 |
| AC | 2 |
| AD | 3 |
| BC | 4 |
| BD | 5 |
| CD | 6 |
Berikut adalah langkah-langkah penerapan algoritma Kruskal:
- Urutkan sisi berdasarkan panjangnya: AB, AC, AD, BC, BD, CD.
- Mulailah dengan set sisi kosong.
- Tambahkan sisi AB ke set sisi. Set sisi sekarang AB.
- Tambahkan sisi AC ke set sisi. Set sisi sekarang AB, AC.
- Tambahkan sisi AD ke set sisi. Set sisi sekarang AB, AC, AD.
- Sisi BC akan menciptakan siklus, jadi sisi ini tidak ditambahkan.
- Sisi BD akan menciptakan siklus, jadi sisi ini tidak ditambahkan.
- Sisi CD akan menciptakan siklus, jadi sisi ini tidak ditambahkan.
Pohon rentang minimum yang dihasilkan adalah AB, AC, AD, dengan total panjang sisi 6.
Algoritma Greedy dalam Pemrograman: Contoh Soal Algoritma Greedy
Algoritma greedy adalah pendekatan untuk memecahkan masalah optimisasi dengan membuat serangkaian pilihan terbaik yang tampaknya optimal pada saat itu, tanpa mempertimbangkan konsekuensi jangka panjang. Strategi ini berusaha mencapai solusi optimal global dengan memilih pilihan terbaik lokal di setiap langkah. Algoritma greedy sering digunakan dalam situasi di mana solusi optimal global sulit ditemukan, dan pendekatan praktis diperlukan.
Contoh Kode Program Sederhana
Berikut adalah contoh kode program sederhana yang menerapkan algoritma greedy untuk menyelesaikan masalah penukaran uang:
Misalnya, kita memiliki uang kertas dengan nilai tertentu, dan kita ingin menukar uang kertas tersebut dengan jumlah uang kertas yang seminimal mungkin. Algoritma greedy akan memilih uang kertas dengan nilai tertinggi yang masih kurang dari atau sama dengan jumlah uang yang ingin ditukar. Proses ini akan berulang sampai jumlah uang yang ingin ditukar habis.
Berikut adalah contoh kode program dalam Python:
def tukar_uang(jumlah_uang, nilai_uang_kertas):
"""
Fungsi untuk menukar uang dengan algoritma greedy.
Args:
jumlah_uang: Jumlah uang yang ingin ditukar.
nilai_uang_kertas: Daftar nilai uang kertas yang tersedia.
Returns:
Kamus yang berisi jumlah setiap uang kertas yang digunakan.
"""
jumlah_uang_kertas =
for nilai in nilai_uang_kertas:
jumlah_uang_kertas[nilai] = 0
for nilai in sorted(nilai_uang_kertas, reverse=True):
while jumlah_uang >= nilai:
jumlah_uang_kertas[nilai] += 1
jumlah_uang -= nilai
return jumlah_uang_kertas
# Contoh penggunaan
jumlah_uang = 1234
nilai_uang_kertas = [1000, 500, 100, 50, 20, 10, 5, 1]
jumlah_uang_kertas = tukar_uang(jumlah_uang, nilai_uang_kertas)
print("Jumlah uang kertas yang digunakan:")
for nilai, jumlah in jumlah_uang_kertas.items():
print(f"nilai: jumlah")
Kode program di atas mendefinisikan fungsi tukar_uang() yang menerima jumlah uang yang ingin ditukar dan daftar nilai uang kertas yang tersedia. Fungsi ini kemudian menggunakan algoritma greedy untuk menentukan jumlah setiap uang kertas yang digunakan.
Implementasi Algoritma Greedy
Implementasi algoritma greedy dapat bervariasi tergantung pada bahasa pemrograman yang digunakan. Namun, secara umum, algoritma greedy melibatkan langkah-langkah berikut:
- Mendeklarasikan variabel untuk menyimpan solusi.
- Mengurutkan pilihan yang tersedia berdasarkan beberapa kriteria.
- Memilih pilihan terbaik yang tersedia pada saat itu dan menambahkannya ke solusi.
- Mengulangi langkah 3 sampai solusi lengkap tercapai.
Diagram Alir Algoritma Greedy
Diagram alir berikut menunjukkan alur logika algoritma greedy dalam kode program untuk masalah penukaran uang:
[Gambar diagram alir yang menunjukkan alur logika algoritma greedy dalam kode program untuk masalah penukaran uang. Diagram alir harus menyertakan langkah-langkah berikut:
1. Mulai
2. Inisialisasi variabel untuk menyimpan solusi.
3. Urutkan pilihan yang tersedia berdasarkan nilai.
4. Pilih pilihan terbaik yang tersedia dan tambahkan ke solusi.
5. Perbarui jumlah uang yang tersisa.
6. Ulangi langkah 4 dan 5 sampai jumlah uang yang tersisa habis.
7. Selesai
]
Diagram alir di atas menunjukkan alur logika algoritma greedy dalam kode program untuk masalah penukaran uang. Algoritma dimulai dengan menginisialisasi variabel untuk menyimpan solusi. Kemudian, pilihan yang tersedia diurutkan berdasarkan nilai. Algoritma kemudian memilih pilihan terbaik yang tersedia dan menambahkannya ke solusi. Proses ini berulang sampai jumlah uang yang tersisa habis.
Aplikasi Algoritma Greedy dalam Kehidupan Nyata
Algoritma greedy, dengan pendekatannya yang sederhana dan efisien, ternyata memiliki aplikasi yang luas dalam kehidupan sehari-hari. Algoritma ini membantu menyelesaikan berbagai masalah kompleks dengan cara memilih solusi terbaik pada setiap langkah, tanpa mempertimbangkan konsekuensi jangka panjang. Mari kita telusuri beberapa contoh aplikasi algoritma greedy yang mungkin tidak disadari, namun telah menjadi bagian integral dari kehidupan kita.
Sistem Navigasi
Algoritma greedy memainkan peran penting dalam sistem navigasi, seperti Google Maps atau Waze. Saat kita mencari rute tercepat dari titik A ke titik B, algoritma ini bekerja dengan memilih jalan terpendek pada setiap persimpangan, dengan asumsi bahwa pilihan tersebut akan mengarah pada rute tercepat secara keseluruhan. Meskipun tidak selalu menghasilkan rute terpendek secara absolut, algoritma greedy umumnya memberikan solusi yang cepat dan efisien, terutama di kota-kota besar dengan banyak persimpangan.
Sistem Pencarian Informasi
Algoritma greedy juga diterapkan dalam sistem pencarian informasi, seperti mesin pencari Google. Saat kita mengetik kata kunci di kotak pencarian, algoritma ini akan secara bertahap menyaring hasil pencarian berdasarkan relevansi, dengan memilih dokumen yang paling relevan dengan kata kunci yang telah diketik. Misalnya, jika kita mengetik “restoran pizza”, algoritma greedy akan menampilkan restoran pizza yang paling dekat dengan lokasi kita, kemudian menyaring berdasarkan rating dan ulasan, hingga akhirnya menampilkan daftar restoran pizza yang paling sesuai dengan kriteria kita.
Ekonomi dan Bisnis
Dalam bidang ekonomi dan bisnis, algoritma greedy digunakan dalam berbagai aplikasi, seperti:
- Manajemen Inventaris: Algoritma greedy dapat digunakan untuk menentukan jumlah optimal produk yang harus dipesan untuk meminimalkan biaya penyimpanan dan kekurangan stok. Algoritma ini akan memilih jumlah produk yang paling menguntungkan pada setiap periode, dengan mempertimbangkan permintaan dan biaya penyimpanan.
- Penjadwalan: Dalam penjadwalan tugas, algoritma greedy dapat digunakan untuk memilih tugas yang paling penting atau mendesak untuk diselesaikan terlebih dahulu, dengan tujuan memaksimalkan efisiensi dan produktivitas.
- Pemilihan Portofolio: Dalam investasi, algoritma greedy dapat digunakan untuk memilih aset yang paling menguntungkan untuk dimasukkan dalam portofolio, dengan tujuan memaksimalkan pengembalian investasi.
Kriteria Evaluasi Algoritma Greedy
Setelah mempelajari konsep dasar algoritma greedy, penting untuk memahami bagaimana mengukur efektivitasnya. Algoritma greedy dirancang untuk memberikan solusi optimal dalam waktu yang singkat, tetapi tidak selalu menjamin hasil yang terbaik. Untuk menilai performa algoritma greedy, kita perlu menggunakan metrik yang tepat untuk mengukur efisiensi dan kualitas solusinya.
Metrik Evaluasi Algoritma Greedy
Beberapa metrik yang umum digunakan untuk mengevaluasi kinerja algoritma greedy meliputi:
- Optimalitas: Apakah algoritma greedy selalu menghasilkan solusi optimal untuk setiap kasus? Metrik ini mengukur seberapa dekat solusi yang dihasilkan dengan solusi optimal yang sebenarnya. Algoritma greedy yang optimal akan menghasilkan solusi yang sama baiknya dengan solusi optimal yang dapat dicapai dengan algoritma lain yang lebih kompleks.
- Kompleksitas Waktu: Berapa lama waktu yang dibutuhkan algoritma greedy untuk menyelesaikan masalah? Kompleksitas waktu mengukur efisiensi algoritma dalam hal jumlah operasi yang dibutuhkan untuk menyelesaikan masalah. Algoritma greedy yang efisien akan memiliki kompleksitas waktu yang rendah, artinya membutuhkan waktu yang lebih sedikit untuk menyelesaikan masalah.
- Kompleksitas Ruang: Berapa banyak ruang memori yang dibutuhkan algoritma greedy untuk beroperasi? Kompleksitas ruang mengukur efisiensi algoritma dalam hal jumlah memori yang dibutuhkan untuk menyimpan data dan melakukan perhitungan. Algoritma greedy yang efisien akan memiliki kompleksitas ruang yang rendah, artinya membutuhkan lebih sedikit memori untuk beroperasi.
- Kejelasan: Apakah algoritma greedy mudah dipahami dan diimplementasikan? Kejelasan mengukur kemudahan algoritma untuk dipahami dan diterapkan. Algoritma greedy yang jelas akan mudah dipahami dan diimplementasikan, sehingga lebih mudah untuk diuji dan dimodifikasi.
- Fleksibilitas: Apakah algoritma greedy dapat diadaptasi untuk menyelesaikan berbagai masalah? Fleksibilitas mengukur seberapa mudah algoritma dapat diadaptasi untuk menyelesaikan masalah yang berbeda. Algoritma greedy yang fleksibel dapat digunakan untuk menyelesaikan berbagai masalah dengan modifikasi minimal.
Tabel Metrik Evaluasi Algoritma Greedy
| Metrik | Definisi | Contoh |
|---|---|---|
| Optimalitas | Seberapa dekat solusi yang dihasilkan dengan solusi optimal yang sebenarnya. | Jika algoritma greedy selalu menghasilkan solusi optimal untuk masalah tertentu, maka optimalitasnya adalah 100%. |
| Kompleksitas Waktu | Jumlah operasi yang dibutuhkan untuk menyelesaikan masalah. | Algoritma greedy dengan kompleksitas waktu O(n) membutuhkan waktu yang sebanding dengan jumlah input (n). |
| Kompleksitas Ruang | Jumlah memori yang dibutuhkan untuk menyimpan data dan melakukan perhitungan. | Algoritma greedy dengan kompleksitas ruang O(1) membutuhkan ruang memori yang konstan, tidak bergantung pada ukuran input. |
| Kejelasan | Kemudahan algoritma untuk dipahami dan diterapkan. | Algoritma greedy yang jelas akan mudah dipahami dan diimplementasikan dengan kode yang sederhana dan mudah dibaca. |
| Fleksibilitas | Seberapa mudah algoritma dapat diadaptasi untuk menyelesaikan masalah yang berbeda. | Algoritma greedy yang fleksibel dapat digunakan untuk menyelesaikan berbagai masalah dengan modifikasi minimal pada kode. |
Pembahasan Lebih Lanjut tentang Algoritma Greedy
Algoritma greedy merupakan salah satu strategi pemecahan masalah yang sangat populer dalam ilmu komputer. Prinsip utamanya adalah memilih solusi terbaik secara lokal di setiap langkah, dengan harapan akan mengarah pada solusi global yang optimal. Meskipun sederhana dan mudah diimplementasikan, algoritma greedy tidak selalu menghasilkan solusi yang optimal. Namun, dalam banyak kasus, algoritma greedy dapat memberikan solusi yang cukup baik dan efisien.
Konsep Algoritma Greedy
Algoritma greedy bekerja dengan membuat serangkaian pilihan optimal secara lokal di setiap langkah. Pilihan optimal ini biasanya didefinisikan berdasarkan fungsi objektif yang ingin dioptimalkan. Tujuan utama algoritma greedy adalah untuk menemukan solusi yang optimal secara global dengan membuat serangkaian pilihan terbaik secara lokal.
Salah satu contoh klasik algoritma greedy adalah masalah penukaran koin. Misalnya, kita ingin menukarkan uang sebesar Rp10.000 dengan jumlah koin yang seminimal mungkin. Algoritma greedy akan memilih koin terbesar terlebih dahulu, yaitu koin Rp5.000, kemudian koin Rp2.000, dan seterusnya, hingga mencapai jumlah yang diinginkan.
Teknik Optimasi pada Algoritma Greedy, Contoh soal algoritma greedy
Meskipun algoritma greedy tidak selalu menghasilkan solusi optimal, ada beberapa teknik optimasi yang dapat diterapkan untuk meningkatkan kualitas solusi yang dihasilkan.
- Teknik Heuristik: Teknik heuristik adalah pendekatan yang tidak menjamin solusi optimal, tetapi seringkali menghasilkan solusi yang cukup baik dalam waktu yang relatif singkat. Teknik ini biasanya digunakan untuk menemukan solusi yang “cukup baik” ketika solusi optimal sulit ditemukan atau terlalu mahal untuk dihitung. Contohnya adalah teknik simulated annealing dan genetic algorithm.
- Teknik Branch and Bound: Teknik ini digunakan untuk mencari solusi optimal dengan mengeksplorasi semua kemungkinan solusi secara sistematis. Teknik ini bekerja dengan membagi ruang solusi menjadi beberapa sub-ruang, dan kemudian mengeliminasi sub-ruang yang tidak mungkin menghasilkan solusi optimal. Teknik ini lebih kompleks daripada teknik heuristik, tetapi dapat menghasilkan solusi optimal.
- Teknik Dynamic Programming: Teknik ini digunakan untuk memecahkan masalah dengan memecahnya menjadi sub-masalah yang lebih kecil. Solusi untuk sub-masalah kemudian digabungkan untuk menghasilkan solusi untuk masalah utama. Teknik ini dapat digunakan untuk mengoptimalkan algoritma greedy dengan menyimpan solusi untuk sub-masalah yang sudah dihitung sebelumnya, sehingga mengurangi waktu komputasi.
Keterbatasan dan Tantangan Algoritma Greedy
Meskipun algoritma greedy memiliki keunggulan dalam kesederhanaan dan efisiensi, algoritma ini memiliki keterbatasan dan tantangan yang perlu dipertimbangkan.
- Tidak Selalu Optimal: Algoritma greedy tidak selalu menghasilkan solusi optimal. Dalam beberapa kasus, pilihan optimal secara lokal tidak selalu mengarah pada solusi optimal secara global. Contohnya, dalam masalah pemilihan aktivitas, memilih aktivitas dengan durasi terpendek di setiap langkah tidak selalu menghasilkan solusi optimal untuk memaksimalkan jumlah aktivitas yang dapat dilakukan.
- Sulit untuk Memilih Fungsi Objektif: Memilih fungsi objektif yang tepat untuk mengukur kualitas solusi adalah hal yang penting dalam algoritma greedy. Fungsi objektif yang tidak tepat dapat menyebabkan algoritma greedy menghasilkan solusi yang buruk.
- Sulit untuk Memilih Strategi Greedy: Memilih strategi greedy yang tepat juga merupakan hal yang penting dalam algoritma greedy. Strategi greedy yang tidak tepat dapat menyebabkan algoritma greedy menghasilkan solusi yang buruk.
Ringkasan Akhir
Memahami contoh soal algoritma greedy membuka pintu menuju dunia pemrograman yang lebih luas. Algoritma ini bukan hanya sekadar teori, tetapi memiliki aplikasi nyata dalam berbagai bidang, mulai dari sistem navigasi hingga sistem pencarian informasi. Dengan mempelajari prinsip kerja dan penerapannya, Anda dapat mengembangkan solusi yang lebih cerdas dan efisien untuk berbagai masalah.