Mempelajari bangun ruang memang menantang, namun dengan latihan yang tepat, Anda akan menguasainya dengan mudah. Contoh Soal Bangun Ruang dan Jawabannya akan menjadi panduan yang membantu Anda memahami konsep-konsep dasar dan mengasah kemampuan dalam menyelesaikan soal-soal.
Artikel ini akan membahas berbagai jenis bangun ruang seperti kubus, balok, tabung, kerucut, dan bola. Anda akan menemukan contoh soal dan jawaban lengkap, disertai penjelasan langkah demi langkah untuk memudahkan pemahaman. Selain itu, artikel ini juga membahas penerapan bangun ruang dalam kehidupan sehari-hari, sehingga Anda dapat melihat langsung manfaatnya.
Jenis-jenis Bangun Ruang
Bangun ruang merupakan bentuk tiga dimensi yang memiliki volume dan luas permukaan. Dalam mempelajari bangun ruang, kita akan mempelajari berbagai jenis bangun ruang, rumus untuk menghitung volume dan luas permukaannya, serta bagaimana menerapkannya dalam kehidupan sehari-hari. Berikut adalah beberapa jenis bangun ruang yang umum dipelajari:
Kubus
Kubus adalah bangun ruang yang memiliki enam sisi berbentuk persegi yang sama besar dan sejajar. Semua rusuk kubus memiliki panjang yang sama. Untuk menghitung volume kubus, kita dapat menggunakan rumus:
Volume kubus = s3
di mana s adalah panjang rusuk kubus.
Lagi pusing ngerjain soal bangun ruang? Tenang, banyak contoh soal dan jawabannya yang bisa kamu temukan di internet. Tapi, jangan lupa juga latihan soal bahasa Inggris buat kelas 12 semester 1, lho! Kamu bisa cek contoh soalnya di situs ini.
Setelah itu, kamu bisa kembali fokus belajar soal bangun ruang dan menguasai materi tersebut dengan lebih mudah.
Contoh Soal
Hitunglah volume kubus dengan panjang rusuk 5 cm.
Penyelesaian:
Volume kubus = s3 = 53 = 125 cm3
Jadi, volume kubus dengan panjang rusuk 5 cm adalah 125 cm3.
Balok
Balok adalah bangun ruang yang memiliki enam sisi berbentuk persegi panjang. Sisi-sisi balok yang berhadapan memiliki ukuran yang sama. Untuk menghitung volume balok, kita dapat menggunakan rumus:
Volume balok = p x l x t
di mana p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
Untuk menghitung luas permukaan balok, kita dapat menggunakan rumus:
Luas permukaan balok = 2(p x l + p x t + l x t)
Contoh Soal
Hitunglah luas permukaan balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 8 cm.
Penyelesaian:
Luas permukaan balok = 2(p x l + p x t + l x t) = 2(10 x 5 + 10 x 8 + 5 x 8) = 2(50 + 80 + 40) = 2(170) = 340 cm2
Jadi, luas permukaan balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 8 cm adalah 340 cm2.
Tabung
Tabung adalah bangun ruang yang memiliki dua sisi berbentuk lingkaran yang sejajar dan kongruen, serta sebuah sisi lengkung yang menghubungkan kedua lingkaran tersebut. Untuk menghitung volume tabung, kita dapat menggunakan rumus:
Volume tabung = πr2t
di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung.
Contoh Soal
Hitunglah volume tabung dengan jari-jari alas 7 cm dan tinggi 12 cm.
Penyelesaian:
Volume tabung = πr2t = π(7)2(12) = π(49)(12) = 588π cm3
Jadi, volume tabung dengan jari-jari alas 7 cm dan tinggi 12 cm adalah 588π cm3.
Kerucut
Kerucut adalah bangun ruang yang memiliki alas berbentuk lingkaran dan sebuah sisi lengkung yang menghubungkan lingkaran alas dengan titik puncak. Untuk menghitung volume kerucut, kita dapat menggunakan rumus:
Volume kerucut = 1/3πr2t
di mana r adalah jari-jari alas kerucut dan t adalah tinggi kerucut.
Untuk menghitung luas permukaan kerucut, kita dapat menggunakan rumus:
Luas permukaan kerucut = πr(r + s)
di mana r adalah jari-jari alas kerucut dan s adalah garis pelukis kerucut.
Contoh Soal
Hitunglah luas permukaan kerucut dengan jari-jari alas 6 cm dan tinggi 8 cm.
Penyelesaian:
Pertama, kita perlu menghitung garis pelukis kerucut (s) dengan menggunakan teorema Pythagoras:
s2 = r2 + t2 = 62 + 82 = 36 + 64 = 100
s = √100 = 10 cm
Kemudian, kita dapat menghitung luas permukaan kerucut:
Luas permukaan kerucut = πr(r + s) = π(6)(6 + 10) = π(6)(16) = 96π cm2
Jadi, luas permukaan kerucut dengan jari-jari alas 6 cm dan tinggi 8 cm adalah 96π cm2.
Bola
Bola adalah bangun ruang yang memiliki semua titik pada permukaannya berjarak sama dari titik pusatnya. Untuk menghitung volume bola, kita dapat menggunakan rumus:
Volume bola = 4/3πr3
di mana r adalah jari-jari bola.
Contoh Soal
Hitunglah volume bola dengan jari-jari 5 cm.
Penyelesaian:
Volume bola = 4/3πr3 = 4/3π(5)3 = 4/3π(125) = 500/3π cm3
Jadi, volume bola dengan jari-jari 5 cm adalah 500/3π cm3.
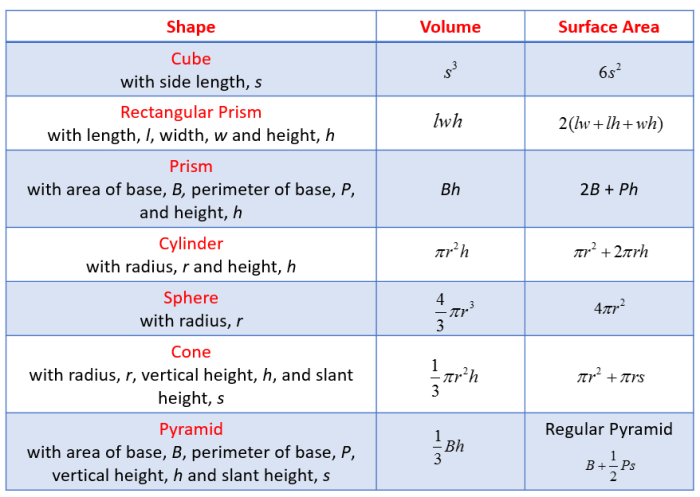
Rumus Bangun Ruang
Bangun ruang merupakan bangun tiga dimensi yang memiliki volume dan luas permukaan. Untuk menghitung volume dan luas permukaan bangun ruang, diperlukan rumus yang tepat. Rumus ini didapatkan berdasarkan bentuk dan sifat dari bangun ruang tersebut. Berikut ini adalah tabel yang berisi jenis bangun ruang, rumus volume, dan rumus luas permukaan:
Rumus Bangun Ruang
| Bangun Ruang | Rumus Volume | Rumus Luas Permukaan |
|---|---|---|
| Kubus | V = s3 | L = 6s2 |
| Balok | V = p x l x t | L = 2(p x l + p x t + l x t) |
| Tabung | V = πr2t | L = 2πr(r + t) |
| Kerucut | V = 1/3πr2t | L = πr(r + s) |
| Limas Segi Empat | V = 1/3 x luas alas x tinggi | L = luas alas + luas keempat sisi tegak |
| Bola | V = 4/3πr3 | L = 4πr2 |
Keterangan:
- s = panjang sisi kubus
- p = panjang balok
- l = lebar balok
- t = tinggi balok
- r = jari-jari lingkaran alas tabung
- t = tinggi tabung
- s = garis pelukis kerucut
Menghitung Volume Kubus
Untuk menghitung volume kubus, kita dapat menggunakan rumus V = s3. Misalnya, jika panjang sisi kubus adalah 5 cm, maka volume kubus adalah:
V = s3 = 53 = 125 cm3
Menghitung Luas Permukaan Balok
Untuk menghitung luas permukaan balok, kita dapat menggunakan rumus L = 2(p x l + p x t + l x t). Misalnya, jika panjang balok adalah 10 cm, lebar balok adalah 5 cm, dan tinggi balok adalah 3 cm, maka luas permukaan balok adalah:
L = 2(p x l + p x t + l x t) = 2(10 x 5 + 10 x 3 + 5 x 3) = 2(50 + 30 + 15) = 2(95) = 190 cm2
Menghitung Volume Tabung, Contoh soal bangun ruang dan jawabannya
Untuk menghitung volume tabung, kita dapat menggunakan rumus V = πr2t. Misalnya, jika jari-jari lingkaran alas tabung adalah 7 cm dan tinggi tabung adalah 10 cm, maka volume tabung adalah:
V = πr2t = π x 72 x 10 = π x 49 x 10 = 490π cm3
Menghitung Luas Permukaan Kerucut
Untuk menghitung luas permukaan kerucut, kita dapat menggunakan rumus L = πr(r + s). Misalnya, jika jari-jari lingkaran alas kerucut adalah 5 cm dan garis pelukis kerucut adalah 13 cm, maka luas permukaan kerucut adalah:
L = πr(r + s) = π x 5(5 + 13) = π x 5 x 18 = 90π cm2
Penerapan Bangun Ruang dalam Kehidupan Sehari-hari
Bangun ruang merupakan bentuk tiga dimensi yang memiliki volume dan luas permukaan. Dalam kehidupan sehari-hari, kita sering menjumpai berbagai macam bangun ruang, mulai dari yang sederhana seperti kubus dan balok hingga yang lebih kompleks seperti tabung dan kerucut. Bangun ruang ini memiliki peran penting dalam berbagai aspek kehidupan, mulai dari konstruksi bangunan hingga desain produk.
Kubus
Kubus merupakan bangun ruang yang memiliki enam sisi persegi yang sama besar dan semua sudutnya siku-siku. Kubus memiliki banyak sekali aplikasi dalam kehidupan sehari-hari, seperti:
- Kotak penyimpanan: Kotak penyimpanan seperti kotak sepatu, kotak mainan, dan kotak perhiasan biasanya berbentuk kubus. Bentuk ini efisien dalam menyimpan barang-barang dengan ukuran yang sama.
- Dadu: Dadu merupakan contoh kubus yang digunakan dalam permainan. Setiap sisi dadu memiliki angka yang berbeda, dan hasil lemparan dadu ditentukan oleh sisi yang menghadap ke atas.
- Rubik’s Cube: Rubik’s Cube merupakan mainan teka-teki yang berbentuk kubus. Setiap sisi kubus terdiri dari 9 kotak kecil yang dapat diputar. Tujuannya adalah untuk menyusun kembali kotak-kotak kecil sehingga setiap sisi kubus memiliki warna yang sama.
Balok
Balok merupakan bangun ruang yang memiliki enam sisi persegi panjang. Sisi-sisi yang berhadapan memiliki ukuran yang sama. Balok memiliki banyak sekali aplikasi dalam kehidupan sehari-hari, seperti:
- Bangunan: Bangunan seperti rumah, gedung, dan jembatan seringkali menggunakan balok sebagai struktur dasarnya. Balok beton digunakan untuk membangun pondasi, kolom, dan balok penyangga.
- Kotak: Kotak-kotak yang digunakan untuk mengemas berbagai produk, seperti kotak sepatu, kotak makanan, dan kotak elektronik, umumnya berbentuk balok. Bentuk ini memungkinkan pengemasan yang efisien dan melindungi produk di dalamnya.
- Batu bata: Batu bata yang digunakan untuk membangun tembok umumnya berbentuk balok. Bentuk ini memungkinkan batu bata disusun secara teratur dan kuat.
Tabung
Tabung merupakan bangun ruang yang memiliki dua sisi lingkaran yang sejajar dan sebuah sisi lengkung yang menghubungkan kedua lingkaran tersebut. Tabung memiliki banyak sekali aplikasi dalam kehidupan sehari-hari, seperti:
- Kaleng minuman: Kaleng minuman seperti kaleng susu, kaleng minuman ringan, dan kaleng minuman energi umumnya berbentuk tabung. Bentuk ini memungkinkan penyimpanan yang efisien dan mudah dibawa.
- Pipa: Pipa yang digunakan untuk mengalirkan air, gas, dan minyak umumnya berbentuk tabung. Bentuk ini memungkinkan aliran fluida yang lancar dan efisien.
- Silinder mesin: Silinder mesin merupakan bagian mesin yang berbentuk tabung. Di dalam silinder, piston bergerak naik turun untuk menghasilkan tenaga.
Kerucut
Kerucut merupakan bangun ruang yang memiliki satu sisi lingkaran dan satu sisi lengkung yang bertemu di sebuah titik puncak. Kerucut memiliki banyak sekali aplikasi dalam kehidupan sehari-hari, seperti:
- Es krim: Es krim cone yang biasa kita makan umumnya berbentuk kerucut. Bentuk ini memungkinkan es krim disimpan dan dimakan dengan mudah.
- Payung: Payung yang biasa kita gunakan untuk melindungi diri dari hujan umumnya berbentuk kerucut. Bentuk ini memungkinkan payung menahan air hujan dengan baik.
- Corong: Corong yang biasa kita gunakan untuk menuangkan cairan ke dalam wadah sempit umumnya berbentuk kerucut. Bentuk ini memungkinkan cairan dituangkan dengan mudah dan terarah.
Bola
Bola merupakan bangun ruang yang berbentuk bulat sempurna. Bola memiliki banyak sekali aplikasi dalam kehidupan sehari-hari, seperti:
- Bola sepak: Bola sepak yang biasa kita mainkan umumnya berbentuk bola. Bentuk ini memungkinkan bola digerakkan dengan mudah dan terarah.
- Bola basket: Bola basket yang biasa kita mainkan umumnya berbentuk bola. Bentuk ini memungkinkan bola digerakkan dengan mudah dan terarah.
- Bumi: Bumi yang kita huni umumnya berbentuk bola. Bentuk ini disebabkan oleh gaya gravitasi yang menarik semua massa ke pusat bumi.
Soal-soal Latihan: Contoh Soal Bangun Ruang Dan Jawabannya
Setelah mempelajari berbagai macam bangun ruang dan rumus-rumus yang terkait, sekarang saatnya kita menguji pemahaman dengan mengerjakan beberapa soal latihan. Soal-soal ini dirancang untuk membantu kamu mengasah kemampuan dalam menghitung volume dan luas permukaan bangun ruang, serta menerapkan konsep bangun ruang dalam kehidupan sehari-hari. Selain itu, kita juga akan mempelajari bagaimana menggabungkan beberapa bangun ruang untuk menghitung volume dan luas permukaannya.
Menghitung Volume dan Luas Permukaan Bangun Ruang
Berikut adalah 5 contoh soal latihan tentang menghitung volume dan luas permukaan bangun ruang:
- Sebuah kubus memiliki panjang rusuk 5 cm. Hitunglah volume dan luas permukaan kubus tersebut.
- Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 8 cm. Hitunglah volume dan luas permukaan balok tersebut.
- Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 12 cm. Hitunglah volume dan luas permukaan tabung tersebut.
- Sebuah kerucut memiliki jari-jari alas 5 cm dan tinggi 12 cm. Hitunglah volume dan luas permukaan kerucut tersebut.
- Sebuah bola memiliki jari-jari 6 cm. Hitunglah volume dan luas permukaan bola tersebut.
Penerapan Bangun Ruang dalam Kehidupan Sehari-hari
Konsep bangun ruang sangat erat kaitannya dengan kehidupan sehari-hari. Berikut adalah 5 contoh soal latihan tentang penerapan bangun ruang dalam kehidupan sehari-hari:
- Sebuah kotak kado berbentuk kubus dengan panjang rusuk 15 cm. Berapa luas kertas kado yang dibutuhkan untuk membungkus kotak kado tersebut?
- Sebuah kolam renang berbentuk balok dengan panjang 10 meter, lebar 5 meter, dan tinggi 2 meter. Berapa liter air yang dibutuhkan untuk mengisi kolam renang tersebut hingga penuh?
- Sebuah kaleng susu berbentuk tabung dengan jari-jari alas 5 cm dan tinggi 12 cm. Berapa volume susu yang dapat ditampung dalam kaleng tersebut?
- Sebuah topi berbentuk kerucut dengan jari-jari alas 10 cm dan tinggi 15 cm. Berapa luas kain yang dibutuhkan untuk membuat topi tersebut?
- Sebuah balon udara berbentuk bola dengan jari-jari 5 meter. Berapa volume udara yang dapat ditampung dalam balon udara tersebut?
Menggabungkan Beberapa Bangun Ruang
Dalam kehidupan sehari-hari, kita seringkali menemukan benda yang merupakan gabungan dari beberapa bangun ruang. Untuk menghitung volume dan luas permukaan benda gabungan, kita perlu memahami cara menggabungkan rumus dari masing-masing bangun ruang penyusunnya.
- Sebuah kotak mainan berbentuk balok dengan panjang 20 cm, lebar 15 cm, dan tinggi 10 cm. Di atas kotak tersebut terdapat sebuah atap berbentuk limas segiempat dengan alas persegi yang memiliki sisi 10 cm dan tinggi 8 cm. Hitunglah volume dan luas permukaan kotak mainan tersebut.
- Sebuah tangki air berbentuk tabung dengan jari-jari alas 1 meter dan tinggi 2 meter. Di atas tangki tersebut terdapat sebuah kerucut dengan jari-jari alas 1 meter dan tinggi 0,5 meter. Hitunglah volume dan luas permukaan tangki air tersebut.
- Sebuah rumah berbentuk balok dengan panjang 10 meter, lebar 6 meter, dan tinggi 4 meter. Di atas rumah tersebut terdapat sebuah atap berbentuk limas segiempat dengan alas persegi yang memiliki sisi 6 meter dan tinggi 3 meter. Hitunglah volume dan luas permukaan rumah tersebut.
- Sebuah tempat pensil berbentuk tabung dengan jari-jari alas 5 cm dan tinggi 15 cm. Di dalam tempat pensil tersebut terdapat sebuah pensil berbentuk silinder dengan jari-jari alas 0,5 cm dan tinggi 10 cm. Hitunglah volume dan luas permukaan tempat pensil tersebut.
- Sebuah vas bunga berbentuk kerucut dengan jari-jari alas 10 cm dan tinggi 20 cm. Di dalam vas tersebut terdapat sebuah bunga berbentuk bola dengan jari-jari 3 cm. Hitunglah volume dan luas permukaan vas bunga tersebut.
Contoh Soal Menghitung Volume Bangun Ruang Gabungan
Berikut adalah contoh soal tentang menghitung volume bangun ruang gabungan:
Sebuah kotak kado berbentuk balok dengan panjang 15 cm, lebar 10 cm, dan tinggi 8 cm. Di atas kotak tersebut terdapat sebuah pita berbentuk setengah bola dengan jari-jari 5 cm. Hitunglah volume kotak kado tersebut!
Untuk menghitung volume kotak kado tersebut, kita perlu menghitung volume balok dan volume setengah bola, kemudian menjumlahkannya. Berikut adalah langkah-langkahnya:
- Hitung volume balok: Volume balok = panjang x lebar x tinggi = 15 cm x 10 cm x 8 cm = 1200 cm3
- Hitung volume setengah bola: Volume setengah bola = (1/2) x (4/3) x π x r3 = (1/2) x (4/3) x 3,14 x 53 = 261,67 cm3
- Jumlahkan volume balok dan volume setengah bola: Volume kotak kado = Volume balok + Volume setengah bola = 1200 cm3 + 261,67 cm3 = 1461,67 cm3
Jadi, volume kotak kado tersebut adalah 1461,67 cm3.
Contoh Soal Menghitung Luas Permukaan Bangun Ruang Gabungan
Berikut adalah contoh soal tentang menghitung luas permukaan bangun ruang gabungan:
Sebuah kaleng susu berbentuk tabung dengan jari-jari alas 7 cm dan tinggi 12 cm. Di atas kaleng tersebut terdapat sebuah tutup berbentuk lingkaran dengan jari-jari 7 cm. Hitunglah luas permukaan kaleng susu tersebut!
Untuk menghitung luas permukaan kaleng susu tersebut, kita perlu menghitung luas permukaan tabung dan luas lingkaran, kemudian menjumlahkannya. Berikut adalah langkah-langkahnya:
- Hitung luas permukaan tabung: Luas permukaan tabung = 2 x π x r x (r + t) = 2 x 3,14 x 7 cm x (7 cm + 12 cm) = 659,4 cm2
- Hitung luas lingkaran: Luas lingkaran = π x r2 = 3,14 x 72 = 153,86 cm2
- Jumlahkan luas permukaan tabung dan luas lingkaran: Luas permukaan kaleng susu = Luas permukaan tabung + Luas lingkaran = 659,4 cm2 + 153,86 cm2 = 813,26 cm2
Jadi, luas permukaan kaleng susu tersebut adalah 813,26 cm2.
Kunci Jawaban
Berikut adalah kunci jawaban untuk soal-soal latihan yang telah dibuat sebelumnya. Setiap jawaban disertai dengan penjelasan langkah-langkah penyelesaian untuk membantu kamu memahami konsep menghitung volume dan luas permukaan bangun ruang gabungan.
Dalam menghitung volume dan luas permukaan bangun ruang gabungan, kita perlu memahami bentuk-bentuk dasar yang menyusun bangun ruang tersebut. Selanjutnya, kita perlu mengidentifikasi rumus yang tepat untuk setiap bentuk dasar dan menerapkannya dengan cermat. Dengan begitu, kita dapat menghitung volume dan luas permukaan bangun ruang gabungan secara akurat.
Soal Latihan dan Jawaban
| No | Soal | Jawaban | Penjelasan |
|---|---|---|---|
| 1 | Hitunglah volume dan luas permukaan bangun ruang gabungan yang terdiri dari kubus dengan panjang rusuk 5 cm dan limas segiempat beraturan dengan panjang rusuk alas 5 cm dan tinggi 4 cm! | Volume: 162,5 cm3 Luas Permukaan: 175 cm2 |
|
| 2 | Sebuah bangun ruang gabungan terdiri dari tabung dengan diameter alas 10 cm dan tinggi 12 cm, serta kerucut dengan diameter alas 10 cm dan tinggi 8 cm. Hitunglah volume dan luas permukaan bangun ruang gabungan tersebut! | Volume: 1.256,64 cm3 Luas Permukaan: 628,32 cm2 |
|
| 3 | Sebuah bangun ruang gabungan terdiri dari balok dengan panjang 8 cm, lebar 6 cm, dan tinggi 5 cm, serta prisma segitiga siku-siku dengan panjang alas 4 cm, tinggi alas 3 cm, dan tinggi prisma 7 cm. Hitunglah volume dan luas permukaan bangun ruang gabungan tersebut! | Volume: 304 cm3 Luas Permukaan: 286 cm2 |
|
Simpulan Akhir
Dengan latihan yang konsisten dan pemahaman yang mendalam, Anda akan semakin mahir dalam menghitung volume dan luas permukaan bangun ruang. Jangan ragu untuk mencoba soal-soal latihan yang telah disediakan dan menguji kemampuan Anda. Selamat belajar dan semoga sukses!





