Contoh soal matriks dalam kehidupan sehari hari – Pernahkah Anda membayangkan bahwa matriks, konsep matematika yang mungkin terasa rumit, ternyata memiliki peran penting dalam kehidupan sehari-hari? Matriks, yang tampak seperti kumpulan angka dalam kotak, menyertai kita dalam berbagai aktivitas, mulai dari mengelola keuangan hingga merencanakan perjalanan.
Bayangkan Anda sedang berbelanja bulanan, mencatat pengeluaran, atau merencanakan perjalanan liburan. Di balik semua itu, matriks dapat membantu Anda mengatur data, menganalisis informasi, dan membuat keputusan yang lebih efektif. Dalam artikel ini, kita akan menjelajahi berbagai contoh soal matriks yang menunjukkan bagaimana konsep ini hadir dalam kehidupan nyata dan membantu kita dalam berbagai bidang.
Contoh Soal Matriks dalam Kehidupan Sehari-hari
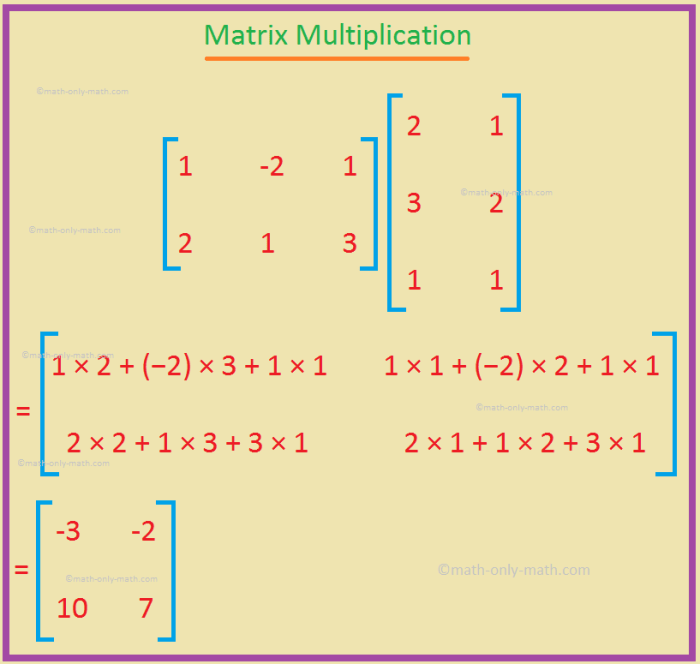

Matriks merupakan alat yang ampuh dalam memodelkan dan menyelesaikan berbagai masalah dalam kehidupan sehari-hari. Matriks dapat membantu dalam mengorganisir data, menyelesaikan sistem persamaan, dan bahkan melakukan perencanaan.
Pengelolaan Keuangan Rumah Tangga
Matriks dapat membantu dalam mencatat pengeluaran bulanan, menganalisis tren pengeluaran, dan membuat anggaran yang lebih efektif.
- Misalnya, Anda dapat membuat matriks untuk mencatat pengeluaran bulanan Anda, dengan kolom untuk kategori pengeluaran (misalnya, makanan, transportasi, hiburan) dan baris untuk setiap minggu dalam bulan tersebut.
- Dengan menggunakan matriks, Anda dapat dengan mudah melihat ke mana uang Anda pergi dan mengidentifikasi area di mana Anda dapat memangkas pengeluaran.
Perencanaan Perjalanan
Matriks dapat digunakan untuk menentukan rute tercepat, menghitung jarak tempuh, dan mengoptimalkan waktu perjalanan.
- Misalnya, Anda dapat membuat matriks jarak antara kota-kota yang ingin Anda kunjungi, dengan kolom dan baris yang mewakili setiap kota.
- Dengan menggunakan matriks, Anda dapat dengan mudah menentukan rute tercepat dan paling efisien untuk perjalanan Anda.
Penjadwalan Kegiatan
Matriks dapat membantu dalam mengatur jadwal kuliah atau kerja, memastikan bahwa semua tugas terselesaikan tepat waktu dan menghindari konflik jadwal.
- Misalnya, Anda dapat membuat matriks dengan kolom untuk hari dalam seminggu dan baris untuk jam dalam hari tersebut.
- Anda kemudian dapat mengisi matriks dengan kegiatan Anda, seperti kuliah, kerja, dan janji temu, untuk memastikan bahwa jadwal Anda teratur dan efisien.
Operasi Matriks dalam Kehidupan Sehari-hari: Contoh Soal Matriks Dalam Kehidupan Sehari Hari
Matriks, yang merupakan susunan bilangan dalam baris dan kolom, ternyata bukan hanya materi pelajaran matematika yang membingungkan. Matriks memiliki aplikasi luas dalam berbagai bidang kehidupan, termasuk ekonomi, teknik, dan bahkan seni.
Contoh soal matriks dalam kehidupan sehari-hari bisa kita temui dalam berbagai bidang, seperti pengaturan jadwal, penjadwalan produksi, hingga perhitungan keuangan. Nah, kalau kamu ingin mempelajari lebih dalam tentang deret angka dan cara menyelesaikannya, kamu bisa cek contoh soal deret angka beserta jawabannya di sini.
Pengetahuan tentang deret angka juga bisa membantu kita memahami dan menyelesaikan soal matriks yang lebih kompleks, lho!
Penjumlahan dan Pengurangan Matriks
Operasi penjumlahan dan pengurangan matriks sangat berguna dalam berbagai situasi sehari-hari. Bayangkan Anda memiliki dua toko yang menjual produk yang sama. Matriks dapat digunakan untuk mencatat jumlah penjualan setiap produk di setiap toko. Dengan menjumlahkan kedua matriks tersebut, Anda dapat mengetahui total penjualan untuk setiap produk di kedua toko.
- Contohnya, jika toko A menjual 10 kaos, 5 celana, dan 3 topi, dan toko B menjual 8 kaos, 7 celana, dan 4 topi, maka total penjualan dapat dihitung dengan menjumlahkan kedua matriks tersebut.
Perkalian Matriks
Perkalian matriks memiliki aplikasi yang lebih luas, khususnya dalam kalkulasi keuangan dan perhitungan jarak.
- Dalam kalkulasi keuangan, perkalian matriks dapat digunakan untuk menghitung total biaya suatu proyek. Misalnya, Anda memiliki matriks yang menunjukkan jumlah jam kerja untuk setiap jenis pekerjaan, dan matriks lain yang menunjukkan biaya per jam untuk setiap jenis pekerjaan. Dengan mengalikan kedua matriks tersebut, Anda dapat memperoleh matriks yang menunjukkan total biaya untuk setiap jenis pekerjaan.
- Perkalian matriks juga dapat digunakan untuk menghitung jarak antara dua titik. Anda dapat merepresentasikan titik-titik tersebut sebagai vektor, dan kemudian mengalikan vektor-vektor tersebut dengan matriks transformasi yang sesuai. Hasilnya akan menjadi vektor yang menunjukkan jarak antara kedua titik tersebut.
Determinan Matriks
Determinan matriks merupakan nilai skalar yang terkait dengan matriks persegi. Determinan memiliki banyak aplikasi, salah satunya adalah dalam menentukan solusi sistem persamaan linear.
- Sistem persamaan linear dapat direpresentasikan dalam bentuk matriks. Jika determinan matriks koefisien sistem persamaan linear tidak sama dengan nol, maka sistem persamaan linear tersebut memiliki solusi unik. Jika determinan matriks koefisien sama dengan nol, maka sistem persamaan linear tersebut mungkin memiliki solusi tak hingga atau tidak memiliki solusi sama sekali.
Contoh Soal Matriks dalam Bidang Ilmu Komputer
Matriks memiliki peran penting dalam berbagai bidang ilmu komputer, termasuk pemrosesan gambar, algoritma pencarian, dan keamanan data. Mari kita bahas contoh soal yang menggambarkan penerapan matriks dalam konteks tersebut.
Pemrosesan Gambar, Contoh soal matriks dalam kehidupan sehari hari
Matriks dapat digunakan untuk merepresentasikan gambar digital. Setiap elemen dalam matriks mewakili nilai intensitas piksel pada gambar. Contoh soal:
- Perubahan warna pada gambar dapat dilakukan dengan mengalikan matriks gambar dengan matriks transformasi warna. Misalkan, untuk mengubah gambar menjadi skala abu-abu, matriks transformasi warna akan memiliki elemen-elemen yang mengubah nilai RGB (Red, Green, Blue) menjadi nilai grayscale.
- Meningkatkan kontras gambar dapat dilakukan dengan mengalikan matriks gambar dengan matriks kontras. Matriks kontras akan memiliki elemen-elemen yang meningkatkan atau mengurangi nilai intensitas piksel, sehingga meningkatkan perbedaan antara area terang dan gelap pada gambar.
Algoritma Pencarian
Matriks dapat digunakan untuk merepresentasikan data dalam database yang besar. Setiap baris dalam matriks mewakili satu data, dan setiap kolom mewakili satu atribut data. Contoh soal:
- Pencarian data dalam database dapat dilakukan dengan menggunakan matriks dan operasi matriks. Misalnya, mencari data yang memenuhi kriteria tertentu dapat dilakukan dengan mengalikan matriks database dengan matriks kriteria. Elemen-elemen dalam matriks kriteria akan mendefinisikan kriteria pencarian.
- Algoritma pencarian seperti pencarian terurut (sorting) dan pencarian biner (binary search) dapat diimplementasikan dengan menggunakan matriks. Matriks dapat digunakan untuk merepresentasikan data yang akan diurutkan atau dicari.
Keamanan Data
Matriks dapat digunakan dalam algoritma enkripsi dan dekripsi data. Enkripsi menggunakan matriks untuk mengubah data asli menjadi bentuk yang tidak dapat dibaca, sedangkan dekripsi menggunakan matriks yang sama untuk mengubah data terenkripsi kembali ke bentuk aslinya. Contoh soal:
- Algoritma enkripsi matriks dapat digunakan untuk mengenkripsi pesan rahasia. Pesan dapat direpresentasikan sebagai matriks, dan matriks enkripsi dapat digunakan untuk mengalikan matriks pesan, sehingga menghasilkan matriks terenkripsi.
- Algoritma dekripsi matriks menggunakan matriks dekripsi yang merupakan invers dari matriks enkripsi. Matriks dekripsi dapat digunakan untuk mengalikan matriks terenkripsi, sehingga menghasilkan matriks pesan asli.
Contoh Soal Matriks dalam Kehidupan Sehari-hari


Matriks merupakan salah satu konsep matematika yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Matriks dapat digunakan untuk menyelesaikan berbagai macam masalah, mulai dari yang sederhana seperti menghitung biaya belanja hingga yang kompleks seperti merancang sistem jaringan komputer.
Untuk memahami bagaimana matriks dapat diterapkan dalam kehidupan sehari-hari, berikut ini beberapa contoh soal yang dapat dipelajari:
Tabel Contoh Soal Matriks dalam Berbagai Bidang
Tabel berikut ini berisi contoh soal matriks dalam berbagai bidang kehidupan sehari-hari. Tabel ini terdiri dari 4 kolom: Bidang, Soal, Penyelesaian, dan Pembahasan. Setiap kolom berisi informasi yang relevan dengan contoh soal yang diberikan.
| Bidang | Soal | Penyelesaian | Pembahasan |
|---|---|---|---|
| Ekonometri | Sebuah perusahaan memiliki 3 pabrik yang memproduksi 2 jenis produk. Pabrik A memproduksi 100 unit produk A dan 50 unit produk B, pabrik B memproduksi 75 unit produk A dan 100 unit produk B, dan pabrik C memproduksi 50 unit produk A dan 75 unit produk B. Jika harga jual produk A adalah Rp 10.000,- dan harga jual produk B adalah Rp 15.000,-, berapa total pendapatan dari ketiga pabrik tersebut? | Dapat diselesaikan dengan menggunakan matriks. Matriks produksi dapat ditulis sebagai berikut:
$$ Matriks harga jual dapat ditulis sebagai berikut: $$ Total pendapatan dari ketiga pabrik dapat dihitung dengan mengalikan matriks produksi dengan matriks harga jual. $$ Jadi, total pendapatan dari pabrik A adalah Rp 1.750.000,-, pabrik B adalah Rp 2.250.000,-, dan pabrik C adalah Rp 1.625.000,-. |
Soal ini menunjukkan bagaimana matriks dapat digunakan untuk menghitung total pendapatan dari beberapa pabrik yang memproduksi berbagai jenis produk. Dengan menggunakan matriks, kita dapat menyelesaikan masalah ini dengan lebih mudah dan efisien. |
| Komputer Grafis | Sebuah gambar 2 dimensi dapat direpresentasikan sebagai matriks. Setiap elemen matriks mewakili warna piksel pada gambar. Misalkan kita ingin memutar gambar 90 derajat searah jarum jam. Bagaimana kita dapat merepresentasikan rotasi ini dengan menggunakan matriks? | Rotasi 90 derajat searah jarum jam dapat direpresentasikan dengan matriks rotasi berikut:
$$ Untuk memutar gambar, kita perlu mengalikan matriks rotasi dengan matriks yang merepresentasikan gambar tersebut. |
Soal ini menunjukkan bagaimana matriks dapat digunakan untuk melakukan transformasi geometri pada gambar 2 dimensi. Dengan menggunakan matriks rotasi, kita dapat memutar gambar tanpa mengubah ukuran atau bentuknya. |
| Jaringan Komputer | Sebuah jaringan komputer dapat direpresentasikan sebagai graf, di mana setiap simpul mewakili sebuah komputer dan setiap sisi mewakili koneksi antara dua komputer. Bagaimana kita dapat menggunakan matriks untuk merepresentasikan jaringan komputer? | Jaringan komputer dapat direpresentasikan dengan matriks adjacency. Matriks adjacency adalah matriks persegi yang berisi informasi tentang koneksi antara simpul-simpul dalam graf. Setiap elemen dalam matriks adjacency merepresentasikan apakah ada koneksi antara dua simpul. Jika ada koneksi, elemen tersebut bernilai 1, jika tidak ada koneksi, elemen tersebut bernilai 0. | Soal ini menunjukkan bagaimana matriks dapat digunakan untuk merepresentasikan jaringan komputer. Dengan menggunakan matriks adjacency, kita dapat menganalisis struktur jaringan komputer dan mencari jalur terpendek antara dua komputer. |
| Kriptografi | Kriptografi adalah ilmu tentang menyembunyikan informasi. Salah satu metode kriptografi yang populer adalah enkripsi matriks. Bagaimana enkripsi matriks bekerja? | Enkripsi matriks bekerja dengan mengalikan matriks kunci dengan matriks teks yang akan dienkripsi. Matriks kunci adalah matriks yang berisi informasi rahasia yang digunakan untuk mengenkripsi dan dekripsi pesan. Matriks teks adalah matriks yang berisi pesan yang akan dienkripsi. | Soal ini menunjukkan bagaimana matriks dapat digunakan untuk mengenkripsi dan dekripsi pesan. Dengan menggunakan enkripsi matriks, kita dapat melindungi informasi rahasia dari pihak yang tidak berwenang. |
Ringkasan Penutup
Memahami konsep matriks dan penerapannya dalam kehidupan sehari-hari membuka perspektif baru tentang bagaimana matematika berperan dalam berbagai aspek kehidupan kita. Dari mengatur keuangan hingga merancang desain grafis, matriks memberikan alat yang kuat untuk mengorganisir, menganalisis, dan menyelesaikan berbagai permasalahan. Semoga contoh-contoh soal yang telah dibahas memberikan gambaran yang lebih jelas tentang bagaimana matriks hadir dalam dunia nyata dan membantu kita dalam berbagai bidang.




