Artikel matematika tentang bangun ruang – Pernahkah Anda memperhatikan bentuk-bentuk benda di sekitar kita? Dari kotak sepatu hingga bola basket, semua benda tersebut memiliki bentuk yang unik dan menarik. Di dunia matematika, bentuk-bentuk tersebut dikenal sebagai bangun ruang. Bangun ruang merupakan objek tiga dimensi yang memiliki panjang, lebar, dan tinggi. Dunia bangun ruang tidak hanya sebatas teori, tetapi juga memiliki aplikasi yang luas dalam kehidupan sehari-hari.
Dalam artikel ini, kita akan menjelajahi dunia bangun ruang dengan lebih dalam. Mulai dari definisi dasar hingga jenis-jenis bangun ruang yang beragam, kita akan mempelajari sifat-sifat, rumus, dan aplikasi praktisnya. Mari kita pelajari bagaimana bentuk-bentuk geometri ini dapat membantu kita memahami dan menyelesaikan berbagai permasalahan di sekitar kita.
Pengenalan Bangun Ruang
Bangun ruang adalah objek tiga dimensi yang memiliki volume dan permukaan. Berbeda dengan bangun datar yang hanya memiliki panjang dan lebar, bangun ruang memiliki panjang, lebar, dan tinggi. Bangun ruang merupakan objek yang kita temui setiap hari dalam kehidupan kita.
Bayangkan sebuah kotak sepatu, bola basket, atau bahkan ruangan tempat kamu berada. Semua itu adalah contoh bangun ruang. Bangun ruang memiliki bentuk yang beragam dan memiliki sifat-sifat yang unik, yang membedakannya dari bangun datar.
Perbedaan Bangun Ruang dan Bangun Datar
Untuk memahami lebih dalam tentang bangun ruang, mari kita bandingkan ciri-ciri bangun ruang dengan bangun datar.
| Ciri | Bangun Ruang | Bangun Datar |
|---|---|---|
| Dimensi | Tiga dimensi (panjang, lebar, tinggi) | Dua dimensi (panjang, lebar) |
| Bentuk | Memiliki volume dan permukaan | Hanya memiliki luas permukaan |
| Contoh | Kubus, balok, bola, tabung, kerucut, limas | Persegi, segitiga, lingkaran, persegi panjang |
Jenis-Jenis Bangun Ruang
Bangun ruang merupakan objek tiga dimensi yang memiliki volume dan luas permukaan. Bangun ruang dapat diklasifikasikan berdasarkan bentuk dan sifatnya. Ada berbagai macam bangun ruang yang kita temui dalam kehidupan sehari-hari, mulai dari yang sederhana seperti kubus dan balok hingga yang lebih kompleks seperti kerucut dan bola.
Klasifikasi Bangun Ruang
Bangun ruang dapat diklasifikasikan berdasarkan bentuk dan sifatnya. Berikut adalah beberapa klasifikasi bangun ruang:
- Berdasarkan bentuk alasnya, bangun ruang dapat dibedakan menjadi prisma, limas, dan bangun ruang sisi lengkung.
- Berdasarkan jumlah sisi, bangun ruang dapat dibedakan menjadi bangun ruang sisi datar dan bangun ruang sisi lengkung.
- Berdasarkan jumlah rusuknya, bangun ruang dapat dibedakan menjadi bangun ruang beraturan dan bangun ruang tidak beraturan.
Kubus, Artikel matematika tentang bangun ruang
Kubus adalah bangun ruang sisi datar yang memiliki enam sisi berbentuk persegi yang kongruen. Semua sudutnya siku-siku dan semua rusuknya sama panjang. Kubus memiliki 12 rusuk, 6 sisi, dan 8 titik sudut.
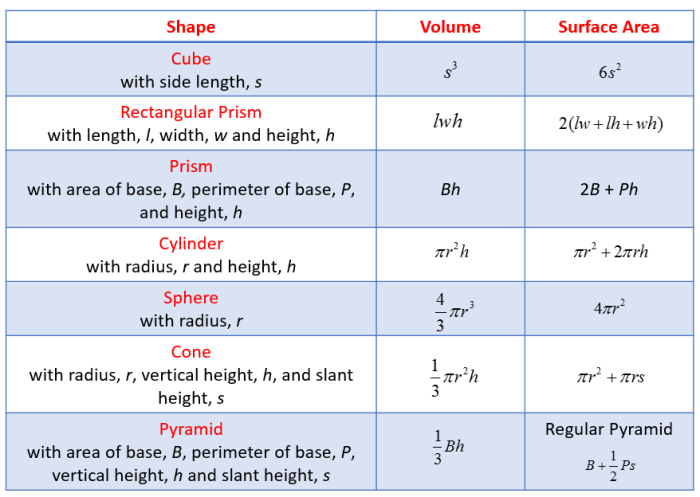
Rumus luas permukaan kubus: 6s2, di mana s adalah panjang sisi kubus.
Rumus volume kubus: s3, di mana s adalah panjang sisi kubus.
Balok
Balok adalah bangun ruang sisi datar yang memiliki enam sisi berbentuk persegi panjang. Semua sudutnya siku-siku dan memiliki tiga pasang sisi yang kongruen. Balok memiliki 12 rusuk, 6 sisi, dan 8 titik sudut.
Rumus luas permukaan balok: 2(pl + pt + lt), di mana p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
Rumus volume balok: p x l x t, di mana p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
Prisma
Prisma adalah bangun ruang sisi datar yang memiliki dua sisi sejajar dan kongruen yang disebut alas dan tutup, serta sisi-sisi tegak yang berbentuk persegi panjang. Sisi tegak prisma tegak lurus terhadap alas dan tutup. Prisma dapat dibedakan menjadi prisma segitiga, prisma segi empat, prisma segi lima, dan seterusnya, tergantung bentuk alasnya.
Rumus luas permukaan prisma: 2 x luas alas + luas sisi tegak.
Rumus volume prisma: luas alas x tinggi prisma.
Limas
Limas adalah bangun ruang sisi datar yang memiliki alas berbentuk segi banyak dan sisi tegak berbentuk segitiga yang bertemu pada satu titik puncak. Limas dapat dibedakan menjadi limas segitiga, limas segi empat, limas segi lima, dan seterusnya, tergantung bentuk alasnya.
Rumus luas permukaan limas: luas alas + luas sisi tegak.
Rumus volume limas: 1/3 x luas alas x tinggi limas.
Tabung
Tabung adalah bangun ruang sisi lengkung yang memiliki dua sisi berbentuk lingkaran yang sejajar dan kongruen yang disebut alas dan tutup, serta sisi lengkung yang menghubungkan alas dan tutup. Sisi lengkung tabung tegak lurus terhadap alas dan tutup.
Rumus luas permukaan tabung: 2 x luas alas + luas sisi lengkung.
Rumus volume tabung: luas alas x tinggi tabung.
Kerucut
Kerucut adalah bangun ruang sisi lengkung yang memiliki alas berbentuk lingkaran dan sisi lengkung yang berbentuk segitiga yang bertemu pada satu titik puncak. Titik puncak kerucut tegak lurus terhadap alas.
Rumus luas permukaan kerucut: luas alas + luas sisi lengkung.
Rumus volume kerucut: 1/3 x luas alas x tinggi kerucut.
Bola
Bola adalah bangun ruang sisi lengkung yang semua titik pada permukaannya berjarak sama dari titik pusat bola. Bola tidak memiliki sisi, rusuk, atau titik sudut.
Rumus luas permukaan bola: 4πr2, di mana r adalah jari-jari bola.
Rumus volume bola: 4/3πr3, di mana r adalah jari-jari bola.
Tabel Rumus Bangun Ruang
| Bangun Ruang | Luas Permukaan | Volume |
|---|---|---|
| Kubus | 6s2 | s3 |
| Balok | 2(pl + pt + lt) | p x l x t |
| Prisma | 2 x luas alas + luas sisi tegak | luas alas x tinggi prisma |
| Limas | luas alas + luas sisi tegak | 1/3 x luas alas x tinggi limas |
| Tabung | 2 x luas alas + luas sisi lengkung | luas alas x tinggi tabung |
| Kerucut | luas alas + luas sisi lengkung | 1/3 x luas alas x tinggi kerucut |
| Bola | 4πr2 | 4/3πr3 |
Rumus dan Aplikasi Bangun Ruang

Setelah mempelajari berbagai jenis bangun ruang, langkah selanjutnya adalah memahami rumus-rumus yang digunakan untuk menghitung luas permukaan dan volume bangun ruang tersebut. Pemahaman ini penting karena memungkinkan kita untuk menghitung ukuran dan kapasitas bangun ruang yang kita temui dalam kehidupan sehari-hari.
Luas Permukaan dan Volume Bangun Ruang
Luas permukaan suatu bangun ruang adalah jumlah luas semua sisi atau permukaan bangun ruang tersebut. Sedangkan volume bangun ruang adalah ukuran ruang yang ditempati oleh bangun ruang tersebut. Rumus untuk menghitung luas permukaan dan volume bangun ruang bervariasi tergantung pada jenis bangun ruangnya.
Contoh Soal dan Penyelesaian
Untuk lebih memahami konsep luas permukaan dan volume bangun ruang, mari kita bahas beberapa contoh soal dan penyelesaiannya.
- Soal 1: Sebuah kubus memiliki panjang rusuk 5 cm. Hitunglah luas permukaan dan volume kubus tersebut.
- Penyelesaian:
- Luas permukaan kubus = 6 x (sisi x sisi) = 6 x (5 cm x 5 cm) = 150 cm2
- Volume kubus = sisi x sisi x sisi = 5 cm x 5 cm x 5 cm = 125 cm3
- Soal 2: Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 4 cm. Hitunglah luas permukaan dan volume balok tersebut.
- Penyelesaian:
- Luas permukaan balok = 2 x (panjang x lebar) + 2 x (panjang x tinggi) + 2 x (lebar x tinggi) = 2 x (10 cm x 6 cm) + 2 x (10 cm x 4 cm) + 2 x (6 cm x 4 cm) = 208 cm2
- Volume balok = panjang x lebar x tinggi = 10 cm x 6 cm x 4 cm = 240 cm3
Aplikasi Bangun Ruang dalam Kehidupan Nyata
Bangun ruang memiliki banyak aplikasi dalam kehidupan nyata, di berbagai bidang seperti arsitektur, teknik, dan desain. Berikut adalah beberapa contohnya:
- Arsitektur: Bangun ruang digunakan dalam perencanaan dan pembangunan gedung, rumah, jembatan, dan struktur lainnya. Misalnya, arsitek menggunakan kubus, balok, dan prisma untuk mendesain ruang interior dan eksterior bangunan.
- Teknik: Bangun ruang digunakan dalam berbagai bidang teknik, seperti teknik sipil, teknik mesin, dan teknik elektro. Misalnya, insinyur sipil menggunakan kubus dan balok untuk mendesain fondasi bangunan, sedangkan insinyur mesin menggunakan silinder dan kerucut untuk mendesain mesin dan peralatan.
- Desain: Bangun ruang digunakan dalam desain produk, seperti mobil, pesawat terbang, dan perabotan rumah tangga. Misalnya, desainer mobil menggunakan silinder dan kerucut untuk mendesain bodi mobil, sedangkan desainer perabotan rumah tangga menggunakan kubus dan balok untuk mendesain meja, kursi, dan lemari.
Konsep Jaring-Jaring Bangun Ruang
Dalam mempelajari bangun ruang, kita seringkali menemukan istilah “jaring-jaring”. Jaring-jaring bangun ruang adalah suatu bentuk datar yang terdiri dari beberapa sisi bangun ruang yang dipotong dan dibentangkan sehingga dapat dilipat kembali menjadi bangun ruang semula. Konsep jaring-jaring ini sangat penting karena membantu kita memahami bagaimana bangun ruang tersusun dan bagaimana cara membuatnya.
Pengertian Jaring-Jaring Bangun Ruang
Jaring-jaring bangun ruang adalah suatu pola yang terbentuk dari sisi-sisi bangun ruang yang dibentangkan sehingga menjadi bangun datar. Dengan kata lain, jaring-jaring merupakan bentuk datar yang dapat dilipat kembali menjadi bangun ruang aslinya. Setiap bangun ruang memiliki jaring-jaring yang unik, tergantung pada bentuk dan jumlah sisi bangun ruang tersebut.
Contoh Jaring-Jaring Bangun Ruang
Berikut adalah contoh jaring-jaring dari beberapa jenis bangun ruang:
- Kubus: Kubus memiliki 6 sisi yang berbentuk persegi. Jaring-jaring kubus terdiri dari 6 persegi yang disusun sedemikian rupa sehingga ketika dilipat, keenam persegi tersebut akan membentuk kubus.
- Balok: Balok memiliki 6 sisi yang berbentuk persegi panjang. Jaring-jaring balok terdiri dari 6 persegi panjang yang disusun sedemikian rupa sehingga ketika dilipat, keenam persegi panjang tersebut akan membentuk balok.
- Limas: Limas memiliki alas berbentuk segi-n dan sisi tegak berbentuk segitiga. Jaring-jaring limas terdiri dari alas dan sisi tegak yang disusun sedemikian rupa sehingga ketika dilipat, alas dan sisi tegak tersebut akan membentuk limas.
- Prisma: Prisma memiliki alas dan tutup berbentuk segi-n dan sisi tegak berbentuk persegi panjang. Jaring-jaring prisma terdiri dari alas, tutup, dan sisi tegak yang disusun sedemikian rupa sehingga ketika dilipat, alas, tutup, dan sisi tegak tersebut akan membentuk prisma.
Ilustrasi Jaring-Jaring Bangun Ruang Kubus dan Balok
Berikut adalah ilustrasi jaring-jaring bangun ruang kubus dan balok yang detail, lengkap dengan keterangan setiap sisi:
Jaring-Jaring Kubus
|
Ilustrasi jaring-jaring kubus adalah seperti ini. Bayangkan enam persegi yang disusun berdampingan, di mana empat persegi membentuk persegi panjang di tengah, dan dua persegi lainnya diposisikan di atas dan di bawah persegi panjang tengah. Ketika dilipat, empat persegi di tengah akan membentuk sisi-sisi kubus, dan dua persegi di atas dan di bawah akan menjadi sisi atas dan bawah kubus. |
Jaring-Jaring Balok
|
Jaring-jaring balok memiliki enam persegi panjang. Bayangkan empat persegi panjang disusun membentuk persegi panjang besar di tengah. Di atas dan di bawah persegi panjang besar, letakkan dua persegi panjang lainnya. Ketika dilipat, keempat persegi panjang di tengah akan membentuk sisi-sisi balok, dan dua persegi panjang di atas dan di bawah akan menjadi sisi atas dan bawah balok. |
Sifat-Sifat Bangun Ruang: Artikel Matematika Tentang Bangun Ruang
Bangun ruang merupakan objek tiga dimensi yang memiliki volume dan permukaan. Bangun ruang memiliki sifat-sifat khusus yang membedakannya dari bangun datar. Sifat-sifat ini meliputi jumlah sisi, rusuk, dan titik sudut, serta konsep diagonal ruang dan diagonal sisi.
Sifat-Sifat Khusus Bangun Ruang
Setiap jenis bangun ruang memiliki sifat-sifat khusus yang membedakannya dari bangun ruang lainnya. Sifat-sifat ini dapat digunakan untuk mengklasifikasikan dan mengidentifikasi jenis bangun ruang.
- Kubus: Kubus memiliki 6 sisi persegi yang sama besar, 12 rusuk yang sama panjang, dan 8 titik sudut.
- Balok: Balok memiliki 6 sisi persegi panjang, 12 rusuk, dan 8 titik sudut.
- Prisma: Prisma memiliki dua sisi yang sejajar dan kongruen (sisi alas dan sisi atas), dan sisi-sisi lainnya berbentuk persegi panjang. Jumlah sisi, rusuk, dan titik sudut prisma tergantung pada bentuk alasnya. Misalnya, prisma segitiga memiliki 5 sisi, 9 rusuk, dan 6 titik sudut.
- Limas: Limas memiliki satu sisi alas dan sisi-sisi lainnya berbentuk segitiga yang bertemu pada satu titik puncak. Jumlah sisi, rusuk, dan titik sudut limas tergantung pada bentuk alasnya. Misalnya, limas segitiga memiliki 4 sisi, 6 rusuk, dan 4 titik sudut.
- Kerucut: Kerucut memiliki satu sisi alas berbentuk lingkaran dan satu sisi lengkung yang bertemu pada satu titik puncak.
- Tabung: Tabung memiliki dua sisi alas berbentuk lingkaran yang sejajar dan kongruen, dan satu sisi lengkung yang menghubungkan kedua alas.
- Bola: Bola merupakan bangun ruang yang semua titik pada permukaannya berjarak sama terhadap satu titik pusat.
Diagonal Ruang dan Diagonal Sisi
Diagonal ruang adalah garis lurus yang menghubungkan dua titik sudut yang tidak terletak pada sisi yang sama. Diagonal sisi adalah garis lurus yang menghubungkan dua titik sudut yang terletak pada sisi yang sama.
Contoh: Pada kubus, terdapat 4 diagonal ruang dan 12 diagonal sisi.
Menentukan Jumlah Diagonal Ruang dan Diagonal Sisi
Untuk menentukan jumlah diagonal ruang dan diagonal sisi pada bangun ruang, kita dapat menggunakan rumus berikut:
- Diagonal ruang: n(n-3)/2, dengan n adalah jumlah titik sudut bangun ruang.
- Diagonal sisi: n(n-1)/2 – s, dengan n adalah jumlah titik sudut bangun ruang dan s adalah jumlah sisi bangun ruang.
Contoh soal: Tentukan jumlah diagonal ruang dan diagonal sisi pada limas segiempat!
Penyelesaian: Limas segiempat memiliki 5 titik sudut. Berdasarkan rumus di atas, jumlah diagonal ruang limas segiempat adalah 5(5-3)/2 = 5. Jumlah diagonal sisi limas segiempat adalah 5(5-1)/2 – 5 = 5.
Kesimpulan
Mempelajari bangun ruang tidak hanya tentang rumus dan teori, tetapi juga tentang memahami bagaimana bentuk-bentuk geometri ini bekerja dalam dunia nyata. Dari desain bangunan hingga pengembangan teknologi, pemahaman tentang bangun ruang menjadi kunci dalam menyelesaikan berbagai tantangan dan menciptakan solusi inovatif. Semoga artikel ini dapat memberikan wawasan baru tentang dunia bangun ruang yang menarik dan penuh manfaat.






