Mempelajari matematika integral bisa terasa rumit, tapi jangan khawatir! Bank soal matematika integral hadir sebagai teman setia dalam perjalanan memahami konsep dan menguasai teknik penyelesaian soal integral. Dari pengertian dasar hingga aplikasi praktis, bank soal ini akan membimbing Anda melalui berbagai jenis soal yang menantang dan mempersiapkan Anda untuk menghadapi ujian dengan percaya diri.
Bank soal ini tidak hanya menyediakan kumpulan soal, tetapi juga dilengkapi dengan pembahasan yang lengkap dan detail. Dengan demikian, Anda dapat memahami konsep integral secara mendalam, mengasah kemampuan menyelesaikan soal, dan menemukan cara terbaik untuk mengaplikasikan integral dalam berbagai bidang seperti fisika, ekonomi, dan teknik.
Pengertian Integral
Integral merupakan salah satu konsep penting dalam matematika yang berhubungan dengan penjumlahan nilai-nilai fungsi dalam suatu interval tertentu. Integral dapat diartikan sebagai kebalikan dari proses diferensial. Dalam diferensial, kita mencari turunan dari suatu fungsi, sedangkan dalam integral, kita mencari fungsi asli dari turunan yang diberikan. Integral memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, teknik, ekonomi, dan ilmu komputer.
Contoh Penerapan Integral dalam Kehidupan Sehari-hari
Integral memiliki banyak aplikasi dalam kehidupan sehari-hari, beberapa contohnya adalah:
- Menghitung luas daerah: Integral dapat digunakan untuk menghitung luas daerah yang dibatasi oleh kurva, garis, dan sumbu koordinat. Contohnya, untuk menghitung luas tanah yang berbentuk kurva, kita dapat menggunakan integral.
- Menghitung volume benda: Integral dapat digunakan untuk menghitung volume benda yang berbentuk tiga dimensi, seperti tabung, kerucut, dan bola. Contohnya, untuk menghitung volume air dalam bak mandi yang berbentuk kerucut, kita dapat menggunakan integral.
- Menghitung jarak tempuh: Integral dapat digunakan untuk menghitung jarak tempuh suatu benda yang bergerak dengan kecepatan tertentu. Contohnya, untuk menghitung jarak tempuh mobil yang bergerak dengan kecepatan tertentu selama waktu tertentu, kita dapat menggunakan integral.
- Menghitung kerja: Integral dapat digunakan untuk menghitung kerja yang dilakukan oleh suatu gaya. Contohnya, untuk menghitung kerja yang dilakukan untuk mengangkat beban ke atas, kita dapat menggunakan integral.
Perbedaan Integral Tentu dan Integral Tak Tentu
Integral dibedakan menjadi dua jenis, yaitu integral tentu dan integral tak tentu. Perbedaan utama antara keduanya terletak pada batasan integrasi. Integral tentu memiliki batasan integrasi yang jelas, sedangkan integral tak tentu tidak memiliki batasan integrasi.
Tabel Perbandingan Integral Tentu dan Integral Tak Tentu
| Fitur | Integral Tentu | Integral Tak Tentu |
|---|---|---|
| Batasan Integrasi | Ada | Tidak ada |
| Hasil | Nilai tunggal | Fungsi |
| Aplikasi | Menghitung luas, volume, kerja | Mencari fungsi asli dari turunan |
Jenis-Jenis Soal Integral
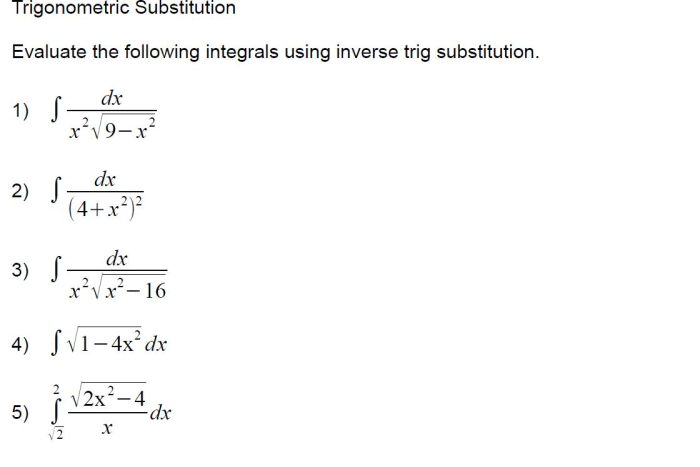
Integral merupakan konsep penting dalam kalkulus yang memiliki berbagai aplikasi dalam berbagai bidang, seperti fisika, teknik, dan ekonomi. Memahami jenis-jenis soal integral dan bagaimana menyelesaikannya merupakan langkah penting dalam menguasai kalkulus.
Integral Tak Tentu
Integral tak tentu adalah operasi kebalikan dari diferensial. Jika turunan dari suatu fungsi f(x) adalah F'(x), maka integral tak tentu dari F'(x) adalah F(x) + C, di mana C adalah konstanta integrasi. Integral tak tentu sering disebut sebagai antiturunan.
- Contoh soal: Tentukan integral tak tentu dari f(x) = 2x + 1.
- Langkah penyelesaian:
- Tentukan antiturunan dari 2x, yaitu x2.
- Tentukan antiturunan dari 1, yaitu x.
- Tambahkan konstanta integrasi C.
Jadi, integral tak tentu dari f(x) = 2x + 1 adalah x2 + x + C.
Integral Tertentu
Integral tertentu adalah integral yang memiliki batas atas dan batas bawah. Integral tertentu menyatakan luas daerah yang dibatasi oleh kurva fungsi, sumbu x, dan dua garis vertikal yang mewakili batas atas dan batas bawah.
- Contoh soal: Tentukan integral tertentu dari f(x) = x2 dari x = 0 hingga x = 2.
- Langkah penyelesaian:
- Tentukan antiturunan dari x2, yaitu (1/3)x3.
- Evaluasi antiturunan pada batas atas dan batas bawah, yaitu (1/3)(2)3 – (1/3)(0)3.
- Hitung selisih kedua hasil evaluasi, yaitu (8/3) – 0 = 8/3.
Jadi, integral tertentu dari f(x) = x2 dari x = 0 hingga x = 2 adalah 8/3.
Integral Substitusi
Integral substitusi adalah teknik untuk menyelesaikan integral yang melibatkan fungsi komposit. Teknik ini melibatkan substitusi variabel baru untuk menyederhanakan integral dan membuatnya lebih mudah diselesaikan.
- Contoh soal: Tentukan integral dari f(x) = (2x + 1)2 dx.
- Langkah penyelesaian:
- Misalkan u = 2x + 1.
- Tentukan du/dx = 2, sehingga dx = du/2.
- Substitusikan u dan dx ke dalam integral, sehingga integral menjadi ∫u2(du/2).
- Selesaikan integral u2(du/2) = (1/6)u3 + C.
- Substitusikan kembali u = 2x + 1, sehingga integral menjadi (1/6)(2x + 1)3 + C.
Jadi, integral dari f(x) = (2x + 1)2 dx adalah (1/6)(2x + 1)3 + C.
Integral Parsial, Bank soal matematika integral
Integral parsial adalah teknik untuk menyelesaikan integral yang melibatkan perkalian dua fungsi. Teknik ini menggunakan rumus integral parsial, yaitu ∫u dv = uv – ∫v du, di mana u dan v adalah fungsi-fungsi yang dapat diturunkan.
- Contoh soal: Tentukan integral dari f(x) = x sin(x) dx.
- Langkah penyelesaian:
- Misalkan u = x dan dv = sin(x) dx.
- Tentukan du = dx dan v = -cos(x).
- Substitusikan u, v, du, dan dv ke dalam rumus integral parsial, sehingga integral menjadi -x cos(x) + ∫cos(x) dx.
- Selesaikan integral cos(x) dx = sin(x) + C.
- Substitusikan kembali hasil integral cos(x) dx, sehingga integral menjadi -x cos(x) + sin(x) + C.
Jadi, integral dari f(x) = x sin(x) dx adalah -x cos(x) + sin(x) + C.
Integral Trigonometri
Integral trigonometri adalah integral yang melibatkan fungsi-fungsi trigonometri, seperti sin(x), cos(x), tan(x), cot(x), sec(x), dan csc(x). Untuk menyelesaikan integral trigonometri, kita perlu menggunakan identitas trigonometri dan teknik-teknik integrasi lainnya.
- Contoh soal: Tentukan integral dari f(x) = sin2(x) dx.
- Langkah penyelesaian:
- Gunakan identitas trigonometri sin2(x) = (1/2)(1 – cos(2x)).
- Substitusikan identitas trigonometri ke dalam integral, sehingga integral menjadi ∫(1/2)(1 – cos(2x)) dx.
- Selesaikan integral (1/2)(1 – cos(2x)) dx = (1/2)(x – (1/2)sin(2x)) + C.
Jadi, integral dari f(x) = sin2(x) dx adalah (1/2)(x – (1/2)sin(2x)) + C.
Integral Pecahan
Integral pecahan adalah integral yang melibatkan fungsi pecahan, seperti 1/(x2 + 1) atau 1/(x2 – 1). Untuk menyelesaikan integral pecahan, kita perlu menggunakan teknik-teknik integrasi yang khusus, seperti dekomposisi pecahan parsial.
- Contoh soal: Tentukan integral dari f(x) = 1/(x2 + 1) dx.
- Langkah penyelesaian:
- Gunakan substitusi u = x, sehingga du = dx.
- Substitusikan u dan du ke dalam integral, sehingga integral menjadi ∫1/(u2 + 1) du.
- Selesaikan integral ∫1/(u2 + 1) du = arctan(u) + C.
- Substitusikan kembali u = x, sehingga integral menjadi arctan(x) + C.
Jadi, integral dari f(x) = 1/(x2 + 1) dx adalah arctan(x) + C.
Integral Fungsi Eksponensial
Integral fungsi eksponensial adalah integral yang melibatkan fungsi eksponensial, seperti ex atau ax. Untuk menyelesaikan integral fungsi eksponensial, kita perlu menggunakan sifat-sifat fungsi eksponensial dan teknik-teknik integrasi lainnya.
- Contoh soal: Tentukan integral dari f(x) = e2x dx.
- Langkah penyelesaian:
- Gunakan substitusi u = 2x, sehingga du = 2 dx.
- Substitusikan u dan du ke dalam integral, sehingga integral menjadi ∫(1/2)eu du.
- Selesaikan integral (1/2)eu du = (1/2)eu + C.
- Substitusikan kembali u = 2x, sehingga integral menjadi (1/2)e2x + C.
Jadi, integral dari f(x) = e2x dx adalah (1/2)e2x + C.
Integral Fungsi Logaritma
Integral fungsi logaritma adalah integral yang melibatkan fungsi logaritma, seperti ln(x). Untuk menyelesaikan integral fungsi logaritma, kita perlu menggunakan teknik-teknik integrasi yang khusus, seperti integral parsial.
- Contoh soal: Tentukan integral dari f(x) = ln(x) dx.
- Langkah penyelesaian:
- Misalkan u = ln(x) dan dv = dx.
- Tentukan du = (1/x) dx dan v = x.
- Substitusikan u, v, du, dan dv ke dalam rumus integral parsial, sehingga integral menjadi x ln(x) – ∫x (1/x) dx.
- Selesaikan integral ∫x (1/x) dx = ∫1 dx = x + C.
- Substitusikan kembali hasil integral ∫x (1/x) dx, sehingga integral menjadi x ln(x) – x + C.
Jadi, integral dari f(x) = ln(x) dx adalah x ln(x) – x + C.
| Jenis Soal Integral | Contoh Soal | Langkah Penyelesaian |
|---|---|---|
| Integral Tak Tentu | Tentukan integral tak tentu dari f(x) = 2x + 1. |
Jadi, integral tak tentu dari f(x) = 2x + 1 adalah x2 + x + C. |
| Integral Tertentu | Tentukan integral tertentu dari f(x) = x2 dari x = 0 hingga x = 2. |
Jadi, integral tertentu dari f(x) = x2 dari x = 0 hingga x = 2 adalah 8/3. |
| Integral Substitusi | Tentukan integral dari f(x) = (2x + 1)2 dx. |
Jadi, integral dari f(x) = (2x + 1)2 dx adalah (1/6)(2x + 1)3 + C. |
| Integral Parsial | Tentukan integral dari f(x) = x sin(x) dx. |
Jadi, integral dari f(x) = x sin(x) dx adalah -x cos(x) + sin(x) + C. |
| Integral Trigonometri | Tentukan integral dari f(x) = sin2(x) dx. |
Jadi, integral dari f(x) = sin2(x) dx adalah (1/2)(x – (1/2)sin(2x)) + C. |
| Integral Pecahan | Tentukan integral dari f(x) = 1/(x2 + 1) dx. |
Jadi, integral dari f(x) = 1/(x2 + 1) dx adalah arctan(x) + C. |
| Integral Fungsi Eksponensial | Tentukan integral dari f(x) = e2x dx. |
Jadi, integral dari f(x) = e2x dx adalah (1/2)e2x + C. |
| Integral Fungsi Logaritma | Tentukan integral dari f(x) = ln(x) dx. |
Jadi, integral dari f(x) = ln(x) dx adalah x ln(x) – x + C. |
Teknik Integrasi
Integrasi merupakan operasi matematika yang merupakan kebalikan dari diferensiasi. Dalam kalkulus, integrasi digunakan untuk mencari luas area di bawah kurva, volume benda putar, dan banyak aplikasi lainnya. Ada berbagai teknik integrasi yang dapat digunakan untuk menyelesaikan integral, dan pemilihan teknik yang tepat tergantung pada bentuk fungsi yang diintegralkan.
Teknik Integrasi Dasar
Teknik integrasi dasar meliputi:
- Integrasi Langsung: Teknik ini digunakan untuk mencari integral fungsi yang sudah diketahui antiturunannya. Contohnya, integral dari x2 adalah (1/3)x3 + C, di mana C adalah konstanta integrasi.
- Integrasi Substitusi: Teknik ini digunakan untuk mengubah variabel integral sehingga integral menjadi lebih mudah diselesaikan. Contohnya, integral dari sin(x)cos(x) dx dapat diselesaikan dengan substitusi u = sin(x).
- Integrasi Per Bagian: Teknik ini digunakan untuk mengintegrasikan hasil kali dua fungsi. Contohnya, integral dari x*sin(x) dx dapat diselesaikan dengan integrasi per bagian.
Teknik Integrasi Lanjutan
Teknik integrasi lanjutan meliputi:
- Integrasi Trigonometri: Teknik ini digunakan untuk mengintegrasikan fungsi trigonometri. Contohnya, integral dari tan(x) dx dapat diselesaikan dengan menggunakan identitas trigonometri.
- Integrasi Parsial: Teknik ini digunakan untuk mengintegrasikan fungsi yang melibatkan turunan dan integral. Contohnya, integral dari x*ex dx dapat diselesaikan dengan integrasi parsial.
- Integrasi Numerik: Teknik ini digunakan untuk mencari aproksimasi integral dengan menggunakan metode numerik. Contohnya, metode trapesium dan metode Simpson.
Contoh Penerapan Teknik Integrasi
| Teknik Integrasi | Contoh Soal | Langkah Penyelesaian |
|---|---|---|
| Integrasi Langsung | ∫x2 dx | 1. Cari antiturunan dari x2, yaitu (1/3)x3. 2. Tambahkan konstanta integrasi C. 3. Hasilnya adalah (1/3)x3 + C. |
| Integrasi Substitusi | ∫sin(x)cos(x) dx | 1. Misalkan u = sin(x). 2. Turunkan u terhadap x, yaitu du/dx = cos(x). 3. Ganti sin(x) dengan u dan cos(x) dx dengan du. 4. Integral menjadi ∫u du. 5. Cari antiturunan dari u, yaitu (1/2)u2. 6. Ganti u dengan sin(x). 7. Hasilnya adalah (1/2)sin2(x) + C. |
| Integrasi Per Bagian | ∫x*sin(x) dx | 1. Misalkan u = x dan dv = sin(x) dx. 2. Turunkan u terhadap x, yaitu du = dx. 3. Cari integral dari dv, yaitu v = -cos(x). 4. Gunakan rumus integrasi per bagian: ∫u dv = uv – ∫v du. 5. Substitusikan nilai u, v, du, dan dv ke dalam rumus. 6. Hasilnya adalah -x*cos(x) + ∫cos(x) dx. 7. Integral dari cos(x) adalah sin(x). 8. Hasil akhirnya adalah -x*cos(x) + sin(x) + C. |
Langkah-langkah Penyelesaian Soal Integral Menggunakan Teknik Substitusi
Berikut adalah langkah-langkah penyelesaian soal integral menggunakan teknik substitusi:
- Pilih substitusi: Pilih substitusi yang akan membuat integral lebih mudah diselesaikan. Biasanya, substitusi dipilih untuk variabel yang rumit dalam integral.
- Tentukan turunan substitusi: Tentukan turunan dari substitusi yang dipilih terhadap variabel asli.
- Ganti variabel dan turunan: Ganti variabel asli dan turunannya dalam integral dengan substitusi dan turunannya.
- Selesaikan integral: Selesaikan integral baru yang lebih sederhana.
- Ganti kembali substitusi: Ganti kembali substitusi dengan variabel asli.
Contoh:
Selesaikan integral ∫(x2 + 1)3 * 2x dx.
- Pilih substitusi u = x2 + 1.
- Tentukan turunan substitusi du/dx = 2x.
- Ganti variabel dan turunan: integral menjadi ∫u3 du.
- Selesaikan integral: ∫u3 du = (1/4)u4 + C.
- Ganti kembali substitusi: (1/4)(x2 + 1)4 + C.
Jadi, integral dari (x2 + 1)3 * 2x dx adalah (1/4)(x2 + 1)4 + C.
Aplikasi Integral: Bank Soal Matematika Integral
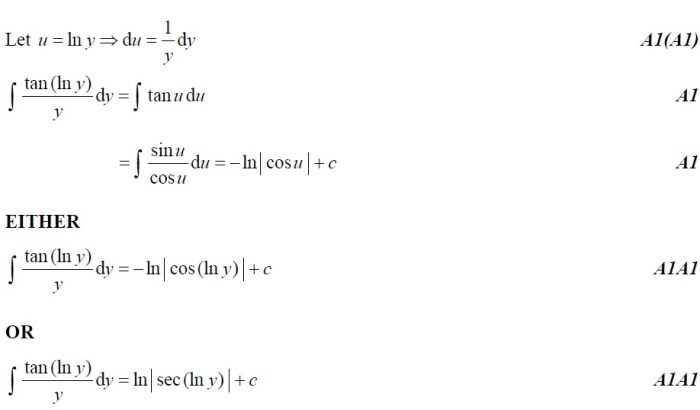
Integral merupakan konsep penting dalam kalkulus yang memiliki aplikasi luas di berbagai bidang. Integral dapat digunakan untuk menyelesaikan masalah-masalah yang melibatkan penjumlahan kontinu, seperti menghitung luas, volume, dan panjang kurva. Selain itu, integral juga memiliki aplikasi penting dalam fisika, ekonomi, dan teknik.
Aplikasi Integral dalam Fisika
Integral berperan penting dalam berbagai bidang fisika. Berikut beberapa contohnya:
- Menghitung Kerja: Integral digunakan untuk menghitung kerja yang dilakukan oleh gaya yang bervariasi terhadap perpindahan. Misalnya, untuk menghitung kerja yang dilakukan oleh pegas yang diregangkan, kita dapat menggunakan integral untuk menjumlahkan gaya yang berubah-ubah selama peregangan.
- Menghitung Energi Potensial: Integral dapat digunakan untuk menghitung energi potensial suatu benda yang dipengaruhi oleh gaya gravitasi. Misalnya, untuk menghitung energi potensial gravitasi suatu benda yang diangkat ke ketinggian tertentu, kita dapat menggunakan integral untuk menjumlahkan gaya gravitasi yang bekerja pada benda tersebut selama pengangkatan.
- Menghitung Momentum: Integral digunakan untuk menghitung momentum suatu benda yang bergerak dengan kecepatan yang bervariasi. Misalnya, untuk menghitung momentum suatu mobil yang sedang melaju dengan kecepatan yang berubah-ubah, kita dapat menggunakan integral untuk menjumlahkan kecepatan mobil tersebut selama periode waktu tertentu.
Aplikasi Integral dalam Ekonomi
Integral juga memiliki aplikasi penting dalam ekonomi, terutama dalam bidang mikroekonomi dan makroekonomi. Berikut beberapa contohnya:
- Menghitung Total Biaya dan Total Pendapatan: Integral dapat digunakan untuk menghitung total biaya produksi dan total pendapatan yang dihasilkan dari penjualan suatu barang atau jasa. Misalnya, untuk menghitung total biaya produksi suatu perusahaan, kita dapat menggunakan integral untuk menjumlahkan biaya variabel dan biaya tetap selama periode waktu tertentu.
- Menghitung Surplus Konsumen dan Surplus Produsen: Integral dapat digunakan untuk menghitung surplus konsumen dan surplus produsen dalam pasar persaingan sempurna. Surplus konsumen adalah selisih antara jumlah yang bersedia dibayar konsumen untuk suatu barang atau jasa dengan harga pasar, sedangkan surplus produsen adalah selisih antara harga pasar dengan biaya produksi.
- Menghitung Pertumbuhan Ekonomi: Integral dapat digunakan untuk menghitung pertumbuhan ekonomi suatu negara atau wilayah. Misalnya, untuk menghitung pertumbuhan ekonomi suatu negara, kita dapat menggunakan integral untuk menjumlahkan perubahan produk domestik bruto (PDB) selama periode waktu tertentu.
Aplikasi Integral dalam Teknik
Integral memiliki aplikasi luas dalam berbagai bidang teknik, seperti teknik sipil, teknik mesin, dan teknik elektro. Berikut beberapa contohnya:
- Menghitung Luas dan Volume: Integral dapat digunakan untuk menghitung luas permukaan dan volume benda tiga dimensi. Misalnya, untuk menghitung luas permukaan suatu silinder, kita dapat menggunakan integral untuk menjumlahkan luas lingkaran yang membentuk permukaan silinder tersebut.
- Menghitung Panjang Kurva: Integral dapat digunakan untuk menghitung panjang kurva yang diberikan dalam bentuk persamaan. Misalnya, untuk menghitung panjang kurva parabola, kita dapat menggunakan integral untuk menjumlahkan panjang segmen kecil yang membentuk kurva tersebut.
- Menghitung Momen Inersia: Integral digunakan untuk menghitung momen inersia suatu benda tegar. Momen inersia merupakan ukuran resistensi suatu benda terhadap perubahan rotasi. Misalnya, untuk menghitung momen inersia suatu silinder, kita dapat menggunakan integral untuk menjumlahkan massa kecil yang membentuk silinder tersebut.
Menghitung Luas Daerah di Bawah Kurva
Integral dapat digunakan untuk menghitung luas daerah di bawah kurva. Berikut langkah-langkah menghitung luas daerah di bawah kurva:
- Tentukan Batas Integrasi: Batas integrasi adalah nilai-nilai x yang menentukan interval di mana kita ingin menghitung luasnya. Misalnya, jika kita ingin menghitung luas daerah di bawah kurva y = x^2 dari x = 0 hingga x = 2, maka batas integrasi adalah 0 dan 2.
- Tentukan Fungsi Integrand: Fungsi integrand adalah fungsi yang mewakili kurva yang ingin kita hitung luasnya. Misalnya, jika kita ingin menghitung luas daerah di bawah kurva y = x^2, maka fungsi integrand adalah x^2.
- Hitung Integral Tertentu: Integral tertentu adalah integral yang dihitung dengan batas integrasi tertentu. Untuk menghitung luas daerah di bawah kurva, kita perlu menghitung integral tertentu dari fungsi integrand dengan batas integrasi yang telah ditentukan. Misalnya, integral tertentu dari x^2 dari 0 hingga 2 adalah:
- Interpretasikan Hasil: Hasil dari integral tertentu adalah luas daerah di bawah kurva. Misalnya, luas daerah di bawah kurva y = x^2 dari x = 0 hingga x = 2 adalah 8/3 satuan luas.
∫02 x^2 dx = [x^3/3]02 = (2^3/3) – (0^3/3) = 8/3
Contoh Soal dan Pembahasan
Setelah mempelajari konsep dasar integral, mari kita berlatih dengan contoh soal yang akan membantu Anda memahami aplikasi integral dalam berbagai konteks. Contoh soal berikut ini akan menguji pemahaman Anda tentang berbagai teknik integrasi dan bagaimana integral digunakan untuk menyelesaikan masalah matematika dan fisika.
Contoh Soal 1: Mencari Luas Area
Misalkan kita ingin mencari luas area yang dibatasi oleh kurva y = x², sumbu x, dan garis x = 2. Bagaimana kita dapat menghitung luas area ini?
Untuk menghitung luas area tersebut, kita dapat menggunakan integral tentu. Kita akan mengintegrasikan fungsi y = x² dari x = 0 hingga x = 2.
Luas = ∫02 x² dx
Hasil dari integral ini adalah:
Luas = [x³/3]02 = (2³/3) – (0³/3) = 8/3
Jadi, luas area yang dibatasi oleh kurva y = x², sumbu x, dan garis x = 2 adalah 8/3 satuan luas.
Contoh Soal 2: Mencari Volume Benda Putar
Bayangkan kita memiliki kurva y = √x dari x = 0 hingga x = 4. Jika kurva ini diputar mengelilingi sumbu x, maka akan membentuk suatu benda putar. Bagaimana kita dapat menghitung volume benda putar ini?
Untuk menghitung volume benda putar, kita dapat menggunakan metode cakram. Metode cakram melibatkan pemotongan benda putar menjadi cakram-cakram tipis, kemudian menjumlahkan volume semua cakram tersebut. Volume setiap cakram dapat dihitung dengan rumus πr²h, di mana r adalah jari-jari cakram dan h adalah tebalnya. Dalam kasus ini, jari-jari cakram adalah y = √x dan tebalnya adalah dx. Kita akan mengintegrasikan volume cakram dari x = 0 hingga x = 4.
Volume = ∫04 π(√x)² dx = ∫04 πx dx
Hasil dari integral ini adalah:
Volume = [πx²/2]04 = (π(4)²/2) – (π(0)²/2) = 8π
Jadi, volume benda putar yang dibentuk oleh kurva y = √x dari x = 0 hingga x = 4 ketika diputar mengelilingi sumbu x adalah 8π satuan volume.
Contoh Soal 3: Mencari Panjang Kurva
Bagaimana kita dapat mencari panjang kurva y = x3/2 dari x = 0 hingga x = 4?
Untuk mencari panjang kurva, kita dapat menggunakan integral garis. Integral garis melibatkan penjumlahan panjang segmen-segmen kecil yang membentuk kurva. Panjang setiap segmen dapat dihitung dengan rumus √(1 + (dy/dx)²) dx. Dalam kasus ini, dy/dx = (3/2)x1/2. Kita akan mengintegrasikan panjang segmen dari x = 0 hingga x = 4.
Panjang Kurva = ∫04 √(1 + ((3/2)x1/2)²) dx = ∫04 √(1 + (9/4)x) dx
Integral ini dapat diselesaikan dengan menggunakan substitusi. Misalkan u = 1 + (9/4)x, maka du = (9/4) dx. Dengan substitusi ini, integral menjadi:
Panjang Kurva = (4/9) ∫110 √u du = (4/9) [(2/3)u3/2]110 = (8/27)(103/2 – 1)
Jadi, panjang kurva y = x3/2 dari x = 0 hingga x = 4 adalah (8/27)(103/2 – 1) satuan panjang.
Penutup
Melalui bank soal matematika integral, Anda akan menemukan bahwa matematika integral tidak sesulit yang dibayangkan. Dengan latihan yang tekun dan pemahaman yang kuat, Anda akan mampu menguasai konsep integral dan mengaplikasikannya dalam berbagai situasi. Selamat belajar dan sukses dalam menaklukkan dunia integral!






