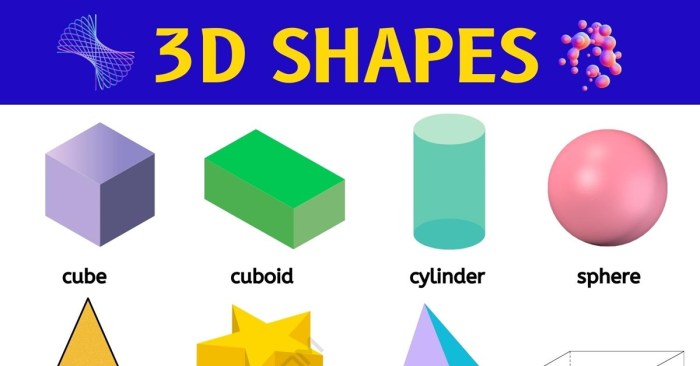
Bentuk bangun ruang dalam bahasa Inggris, atau solid shapes, merupakan konsep dasar dalam geometri yang mempelajari objek tiga dimensi. Dari kubus sederhana hingga kerucut yang rumit, memahami bangun ruang membantu kita memahami dunia di sekitar kita. Bayangkan sebuah rumah, mobil, atau bahkan bola basket – semua objek ini memiliki bentuk bangun ruang yang unik.
Dalam geometri, bangun ruang didefinisikan sebagai objek yang memiliki tiga dimensi: panjang, lebar, dan tinggi. Berbeda dengan bangun datar yang hanya memiliki dua dimensi, bangun ruang memiliki volume dan luas permukaan. Memahami konsep ini membuka pintu untuk mempelajari rumus, perhitungan, dan aplikasi bangun ruang dalam berbagai bidang, mulai dari arsitektur hingga teknologi.
Types of Three-Dimensional Shapes in English
Three-dimensional shapes, also known as solids, are geometric figures that have three dimensions: length, width, and height. They occupy space and have volume. Understanding these shapes is fundamental in geometry and has applications in various fields, such as architecture, engineering, and design.
Types of Three-Dimensional Shapes
There are numerous types of three-dimensional shapes, each with its unique characteristics and properties. Here’s a table summarizing some of the most common ones:
| Shape | Image | Characteristics |
|---|---|---|
| Cube | A cube is a three-dimensional shape with six square faces, all of equal size. It has twelve edges and eight vertices. All angles are right angles. | |
| Cuboid | A cuboid is a three-dimensional shape with six rectangular faces. It has twelve edges and eight vertices. All angles are right angles. | |
| Sphere | A sphere is a three-dimensional shape where all points on its surface are equidistant from a central point. It has no edges or vertices. | |
| Cone | A cone is a three-dimensional shape with a circular base and a curved surface that tapers to a point called the apex. It has one vertex and one edge. | |
| Cylinder | A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface. It has no vertices and two edges. | |
| Pyramid | A pyramid is a three-dimensional shape with a polygonal base and triangular faces that meet at a point called the apex. The number of triangular faces is equal to the number of sides of the base. | |
| Prism | A prism is a three-dimensional shape with two identical and parallel polygonal bases connected by rectangular faces. The number of rectangular faces is equal to the number of sides of the base. |
Perbedaan Bangun Ruang dalam Bahasa Inggris dan Indonesia: Bentuk Bangun Ruang Dalam Bahasa Inggris
Bangun ruang adalah objek tiga dimensi yang memiliki volume dan permukaan. Dalam bahasa Inggris, bangun ruang disebut dengan “solid shapes” atau “three-dimensional shapes”. Perbedaan terminologi antara bahasa Inggris dan Indonesia dalam bangun ruang dapat terlihat pada nama-nama bangun ruang itu sendiri. Berikut adalah tabel yang menunjukkan perbedaan nama bangun ruang dalam bahasa Inggris dan Indonesia.
Perbedaan Nama Bangun Ruang
| Nama Bangun Ruang dalam Bahasa Inggris | Nama Bangun Ruang dalam Bahasa Indonesia |
|---|---|
| Cube | Kubus |
| Cuboid | Balok |
| Sphere | Bola |
| Cone | Kerucut |
| Cylinder | Tabung |
| Pyramid | Limas |
| Prism | Prisma |
Selain nama bangun ruang, terdapat perbedaan terminologi dalam bahasa Inggris dan Indonesia yang berkaitan dengan bangun ruang. Misalnya, dalam bahasa Inggris, “volume” disebut dengan “volume”, sedangkan dalam bahasa Indonesia, “volume” disebut dengan “isi”. Begitu pula dengan “surface area” yang dalam bahasa Indonesia disebut dengan “luas permukaan”.
Contoh Kalimat, Bentuk bangun ruang dalam bahasa inggris
Berikut adalah contoh kalimat yang menggunakan istilah bangun ruang dalam bahasa Inggris dan Indonesia:
- Bahasa Inggris: The cube has six square faces.
Bahasa Indonesia: Kubus memiliki enam sisi persegi. - Bahasa Inggris: The volume of the cylinder is calculated by multiplying the area of the base by the height.
Bahasa Indonesia: Isi tabung dihitung dengan mengalikan luas alas dengan tingginya.
Contoh Soal dan Pembahasan Bangun Ruang dalam Bahasa Inggris
In this section, we will explore some examples of multiple-choice and essay questions related to solid geometry, along with their comprehensive solutions. These examples will help you understand the fundamental concepts and formulas used in solving problems involving solid figures. By studying these examples, you will gain a deeper understanding of how to apply the principles of solid geometry to real-world scenarios.
Multiple Choice Questions
Multiple-choice questions are a common format for testing your understanding of solid geometry concepts. Here are a few examples:
- A rectangular prism has a length of 5 cm, a width of 3 cm, and a height of 4 cm. What is its volume?
- A cylinder has a radius of 7 cm and a height of 10 cm. What is its surface area?
- A cone has a radius of 5 cm and a height of 12 cm. What is its slant height?
- A sphere has a radius of 6 cm. What is its volume?
Essay Questions
Essay questions require you to demonstrate your understanding of solid geometry concepts in a more detailed and analytical way. Here are some examples:
- Explain the difference between a cube and a rectangular prism. Provide examples of real-world objects that represent each shape.
- Derive the formula for the volume of a pyramid. Explain the steps involved in the derivation.
- Discuss the relationship between the surface area and volume of a sphere. How does changing the radius affect these quantities?
- A cylindrical tank with a diameter of 4 meters and a height of 6 meters is filled with water. Calculate the volume of water in the tank. If the water is drained at a rate of 2 cubic meters per minute, how long will it take to empty the tank?
Pembahasan Soal
Multiple Choice Questions
Let’s go through the solutions for the multiple-choice questions:
- The volume of a rectangular prism is calculated by multiplying its length, width, and height. Therefore, the volume of the given rectangular prism is 5 cm x 3 cm x 4 cm = 60 cubic centimeters.
- The surface area of a cylinder is calculated by adding the areas of its two circular bases and its lateral surface. The area of each base is πr², where r is the radius. The lateral surface area is 2πrh, where h is the height. Therefore, the surface area of the given cylinder is 2π(7 cm)² + 2π(7 cm)(10 cm) = 523.6 square centimeters.
- The slant height of a cone is the distance from the apex of the cone to a point on the circumference of its base. It can be calculated using the Pythagorean theorem: slant height² = height² + radius². Therefore, the slant height of the given cone is √(12 cm)² + (5 cm)² = 13 cm.
- The volume of a sphere is calculated by the formula (4/3)πr³, where r is the radius. Therefore, the volume of the given sphere is (4/3)π(6 cm)³ = 904.8 cubic centimeters.
Essay Questions
Let’s delve into the solutions for the essay questions:
- A cube is a special type of rectangular prism where all six sides are squares of equal size. Both shapes have six rectangular faces, but a cube has all sides equal, while a rectangular prism can have different lengths, widths, and heights. Examples of real-world objects that represent a cube include a dice or a sugar cube. A rectangular prism can be seen in a brick or a box.
- The formula for the volume of a pyramid is V = (1/3)Bh, where B is the area of the base and h is the height of the pyramid. The derivation involves dividing the pyramid into infinitesimally small slices, each with a base area of ΔB and a height of Δh. The volume of each slice is approximately ΔBΔh. Summing up the volumes of all the slices and taking the limit as Δh approaches zero, we obtain the formula V = (1/3)Bh.
- The surface area of a sphere is 4πr², and its volume is (4/3)πr³. As the radius increases, both the surface area and volume increase. However, the volume increases at a faster rate than the surface area. This is because the volume is proportional to the cube of the radius, while the surface area is proportional to the square of the radius. This means that a small increase in the radius leads to a much larger increase in the volume compared to the surface area.
- The volume of the cylindrical tank is πr²h = π(2 meters)²(6 meters) = 75.4 cubic meters. To empty the tank at a rate of 2 cubic meters per minute, it will take 75.4 cubic meters / 2 cubic meters per minute = 37.7 minutes.
Sumber Referensi Bangun Ruang dalam Bahasa Inggris

Belajar bangun ruang dalam bahasa Inggris dapat memperluas pemahaman dan kemampuan Anda dalam matematika. Banyak sumber referensi yang tersedia untuk membantu Anda mempelajari konsep-konsep bangun ruang dengan lebih mendalam. Artikel ini akan membahas beberapa buku, website, dan sumber referensi lainnya yang dapat Anda gunakan untuk mempelajari bangun ruang dalam bahasa Inggris, mulai dari tingkat pemula hingga tingkat lanjut.
Buku
Buku merupakan sumber referensi yang sangat baik untuk mempelajari bangun ruang. Buku-buku berikut ini dapat menjadi referensi yang baik untuk Anda:
- Geometry for Dummies oleh Mark Ryan. Buku ini merupakan panduan yang mudah dipahami untuk mempelajari geometri, termasuk bangun ruang, untuk pemula. Buku ini ditulis dengan gaya yang santai dan dilengkapi dengan ilustrasi yang mudah dipahami.
- Solid Geometry oleh David A. Brannan, Matthew F. Esplen, dan Jeremy J. Gray. Buku ini merupakan buku teks yang komprehensif untuk mempelajari geometri, termasuk bangun ruang, untuk tingkat menengah dan lanjut. Buku ini membahas berbagai topik, mulai dari dasar-dasar geometri hingga topik yang lebih kompleks seperti geometri non-Euclidean.
- The Geometry of Space and Time oleh James A. Bedford. Buku ini membahas geometri ruang-waktu, yang merupakan konsep penting dalam fisika modern. Buku ini ditulis dengan gaya yang mudah dipahami dan dilengkapi dengan ilustrasi yang menarik.
Website
Selain buku, website juga merupakan sumber referensi yang baik untuk mempelajari bangun ruang. Berikut ini beberapa website yang dapat Anda gunakan:
- Khan Academy adalah website yang menyediakan berbagai video pembelajaran dan latihan interaktif untuk berbagai mata pelajaran, termasuk matematika. Khan Academy memiliki banyak video pembelajaran tentang bangun ruang yang dapat membantu Anda memahami konsep-konsep dasar dan topik yang lebih kompleks.
- Math Planet adalah website yang menyediakan berbagai materi pembelajaran matematika, termasuk geometri dan bangun ruang. Website ini menyediakan materi pembelajaran yang lengkap dan mudah dipahami, serta latihan soal untuk menguji pemahaman Anda.
- GeoGebra adalah software matematika yang dapat digunakan untuk mempelajari geometri, termasuk bangun ruang. Software ini memungkinkan Anda untuk membuat model 3D dan melakukan simulasi untuk mempelajari konsep-konsep bangun ruang secara visual.
Sumber Referensi Lainnya
Selain buku dan website, Anda juga dapat menemukan sumber referensi lainnya untuk mempelajari bangun ruang, seperti:
- Artikel ilmiah. Artikel ilmiah dapat memberikan informasi yang lebih mendalam dan terkini tentang topik-topik tertentu dalam bangun ruang. Anda dapat menemukan artikel ilmiah di jurnal ilmiah seperti The American Mathematical Monthly dan The Journal of Geometry.
- Forum online. Forum online seperti Math Stack Exchange dapat menjadi tempat yang baik untuk bertanya dan berdiskusi tentang topik-topik tertentu dalam bangun ruang. Anda dapat menemukan jawaban atas pertanyaan Anda dan mendapatkan bantuan dari ahli matematika lainnya.
Kaitan Bangun Ruang dengan Bidang Lainnya
Bangun ruang, dengan bentuknya yang tiga dimensi, memiliki kaitan erat dengan berbagai bidang ilmu pengetahuan. Tidak hanya dalam matematika, konsep bangun ruang juga diterapkan dalam berbagai disiplin ilmu lain, seperti fisika, kimia, biologi, arsitektur, desain, dan teknologi.
Kaitan Bangun Ruang dengan Bidang Matematika Lainnya
Bangun ruang memiliki keterkaitan yang kuat dengan aljabar dan trigonometri. Dalam aljabar, bangun ruang digunakan untuk menyelesaikan masalah yang melibatkan volume, luas permukaan, dan jarak. Contohnya, menghitung volume sebuah kubus atau luas permukaan sebuah limas.
Trigonometri, di sisi lain, digunakan untuk menghitung sudut, panjang sisi, dan hubungan antara sudut dan sisi dalam bangun ruang. Contohnya, menghitung tinggi sebuah piramida atau sudut antara dua bidang dalam sebuah prisma.
Aplikasi Bangun Ruang dalam Bidang Fisika, Kimia, dan Biologi
Bangun ruang memiliki peran penting dalam memahami konsep-konsep dasar di berbagai bidang ilmu, seperti fisika, kimia, dan biologi. Berikut beberapa contohnya:
- Fisika: Konsep bangun ruang digunakan dalam fisika untuk memahami gerakan benda, gaya gravitasi, dan gelombang. Contohnya, menghitung volume dan massa jenis benda, menganalisis gerakan benda yang bergerak dalam ruang, dan memahami sifat gelombang elektromagnetik.
- Kimia: Bangun ruang digunakan dalam kimia untuk menggambarkan struktur molekul, mengidentifikasi jenis ikatan kimia, dan memahami reaksi kimia. Contohnya, model bola dan tongkat digunakan untuk menggambarkan struktur molekul, dan geometri molekul menentukan sifat-sifat molekul, seperti titik didih dan titik leleh.
- Biologi: Bangun ruang digunakan dalam biologi untuk memahami struktur sel, organ, dan jaringan tubuh. Contohnya, model 3D sel digunakan untuk mempelajari struktur dan fungsi organel sel, dan model 3D organ digunakan untuk mempelajari struktur dan fungsi organ tubuh.
Penggunaan Bangun Ruang dalam Bidang Arsitektur, Desain, dan Teknologi
Konsep bangun ruang sangat penting dalam bidang arsitektur, desain, dan teknologi. Berikut beberapa contohnya:
- Arsitektur: Bangun ruang digunakan dalam arsitektur untuk merancang bangunan, menentukan bentuk dan ukuran ruangan, dan menghitung volume dan luas permukaan bangunan. Contohnya, penggunaan bentuk kubus, prisma, dan limas dalam desain bangunan, dan penggunaan model 3D untuk memvisualisasikan desain bangunan.
- Desain: Bangun ruang digunakan dalam desain untuk menciptakan objek yang estetis dan fungsional. Contohnya, penggunaan bentuk silinder dalam desain botol minuman, dan penggunaan bentuk bola dalam desain lampu.
- Teknologi: Bangun ruang digunakan dalam teknologi untuk merancang berbagai macam alat dan mesin. Contohnya, penggunaan bentuk kerucut dalam desain roket, dan penggunaan bentuk kubus dalam desain komputer.
Ringkasan Akhir
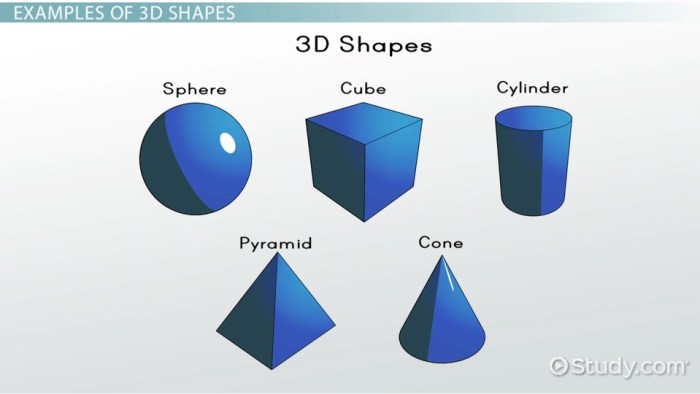
Mempelajari bentuk bangun ruang dalam bahasa Inggris tidak hanya memperkaya pengetahuan geometri kita, tetapi juga membuka perspektif baru dalam memahami dunia sekitar. Dengan pemahaman yang kuat tentang konsep ini, kita dapat mengapresiasi desain bangunan, memahami prinsip kerja mesin, dan bahkan mengagumi keindahan alam yang tercipta dari berbagai bentuk bangun ruang.