Cara hitung r tabel – Anda ingin memahami bagaimana menghitung R tabel? R tabel, atau tabel distribusi t, adalah alat penting dalam statistik yang digunakan untuk menguji hipotesis. Bayangkan Anda sedang melakukan penelitian tentang efektivitas suatu program kesehatan. R tabel membantu Anda menentukan apakah perbedaan yang Anda temukan dalam data penelitian Anda signifikan secara statistik, atau hanya kebetulan. Dengan memahami cara menghitung R tabel, Anda dapat menguji hipotesis dengan lebih akurat dan menarik kesimpulan yang lebih valid dari data penelitian Anda.
Artikel ini akan membahas langkah-langkah menghitung R tabel, faktor-faktor yang memengaruhi nilai R tabel, dan bagaimana menggunakannya dalam analisis data. Kami akan membahas contoh perhitungan, diagram, dan kasus penelitian untuk memberikan pemahaman yang lebih mendalam tentang R tabel.
Cara Menghitung R Tabel
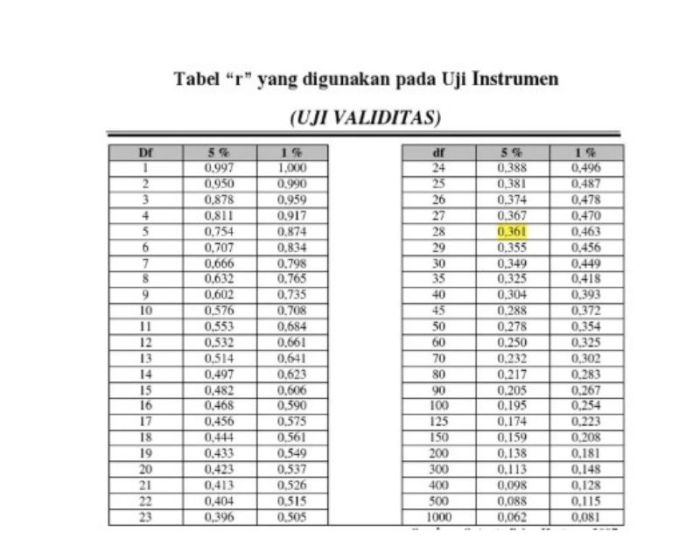
R tabel, juga dikenal sebagai tabel distribusi t, adalah tabel statistik yang digunakan untuk menentukan nilai kritis dalam uji hipotesis. Nilai kritis ini membantu kita dalam menentukan apakah hasil uji signifikan secara statistik atau tidak. Dalam artikel ini, kita akan membahas cara menghitung R tabel, dengan langkah-langkah yang mudah diikuti, contoh perhitungan, dan penjelasan penggunaan tabel distribusi t.
Langkah-langkah Menghitung R Tabel
Berikut adalah langkah-langkah yang dapat Anda ikuti untuk menghitung R tabel:
- Tentukan derajat kebebasan (df) dari sampel Anda. Derajat kebebasan adalah jumlah pengamatan dalam sampel dikurangi 1. Misalnya, jika Anda memiliki 10 pengamatan, maka derajat kebebasan Anda adalah 9 (10 – 1 = 9).
- Tentukan tingkat signifikansi (α) untuk uji Anda. Tingkat signifikansi adalah probabilitas menolak hipotesis nol ketika hipotesis nol sebenarnya benar. Tingkat signifikansi yang umum digunakan adalah 0,05 atau 5%.
- Cari nilai kritis dalam tabel distribusi t yang sesuai dengan derajat kebebasan dan tingkat signifikansi Anda. Tabel distribusi t dapat ditemukan di buku teks statistik atau online.
- Nilai kritis yang Anda temukan dalam tabel distribusi t adalah nilai R tabel Anda.
Contoh Perhitungan R Tabel, Cara hitung r tabel
Misalnya, Anda ingin menguji hipotesis bahwa rata-rata tinggi badan mahasiswa di sebuah universitas adalah 170 cm. Anda mengambil sampel 20 mahasiswa dan menemukan rata-rata tinggi badan mereka adalah 172 cm dengan standar deviasi 5 cm. Anda ingin menggunakan tingkat signifikansi 0,05.
Berikut adalah langkah-langkah untuk menghitung R tabel:
- Derajat kebebasan (df) = 20 – 1 = 19.
- Tingkat signifikansi (α) = 0,05.
- Cari nilai kritis dalam tabel distribusi t dengan df = 19 dan α = 0,05. Nilai kritis yang Anda temukan adalah 2,093.
- Nilai kritis 2,093 adalah R tabel Anda.
Penggunaan Tabel Distribusi T
Tabel distribusi t digunakan untuk menentukan nilai kritis R tabel. Tabel ini menunjukkan nilai-nilai kritis untuk berbagai derajat kebebasan dan tingkat signifikansi. Nilai kritis ini digunakan untuk menentukan apakah hasil uji signifikan secara statistik atau tidak.
Dalam contoh di atas, nilai kritis 2,093 menunjukkan bahwa jika nilai t-hitung (yang dihitung dari data sampel) lebih besar dari 2,093, maka kita dapat menolak hipotesis nol. Ini berarti bahwa rata-rata tinggi badan mahasiswa di universitas tersebut secara signifikan berbeda dari 170 cm.
Aplikasi R Tabel: Cara Hitung R Tabel

R tabel, juga dikenal sebagai tabel kontingensi, merupakan alat yang ampuh dalam analisis data, terutama dalam pengujian hipotesis. Tabel ini memungkinkan kita untuk menyelidiki hubungan antara dua variabel kategorikal, membantu kita memahami apakah ada pola atau ketergantungan yang signifikan antara kedua variabel tersebut.
Cara R Tabel Digunakan untuk Menguji Hipotesis
R tabel membantu kita menguji hipotesis dengan membandingkan frekuensi yang diamati dalam data dengan frekuensi yang diharapkan jika tidak ada hubungan antara variabel. Prosesnya melibatkan langkah-langkah berikut:
- Membangun Hipotesis Nol dan Hipotesis Alternatif: Hipotesis nol menyatakan bahwa tidak ada hubungan antara variabel, sedangkan hipotesis alternatif menyatakan bahwa ada hubungan antara variabel.
- Menghitung Frekuensi yang Diharapkan: Frekuensi yang diharapkan dihitung berdasarkan asumsi bahwa tidak ada hubungan antara variabel. Rumus untuk menghitung frekuensi yang diharapkan adalah (total baris * total kolom) / total sampel.
- Menghitung Statistik Uji: Statistik uji, biasanya Chi-Square, dihitung untuk mengukur perbedaan antara frekuensi yang diamati dan frekuensi yang diharapkan. Semakin besar perbedaannya, semakin kuat bukti untuk menolak hipotesis nol.
- Menentukan Nilai P: Nilai p adalah probabilitas mendapatkan hasil yang diamati atau lebih ekstrem jika hipotesis nol benar. Nilai p yang rendah menunjukkan bahwa hasil yang diamati tidak mungkin terjadi jika hipotesis nol benar, sehingga kita menolak hipotesis nol.
- Menentukan Keputusan: Jika nilai p lebih kecil dari tingkat signifikansi yang ditentukan (biasanya 0,05), kita menolak hipotesis nol. Ini berarti bahwa ada bukti yang cukup untuk mendukung hipotesis alternatif, yang menunjukkan bahwa ada hubungan antara variabel.
Contoh Kasus Penelitian
Misalnya, kita ingin menyelidiki apakah ada hubungan antara jenis kelamin dan preferensi untuk jenis film tertentu. Kita mengumpulkan data dari sampel 100 orang, menanyakan jenis kelamin mereka dan jenis film yang mereka sukai (aksi, komedi, drama). Kita dapat menggunakan R tabel untuk menguji hipotesis bahwa tidak ada hubungan antara jenis kelamin dan preferensi film.
Kita dapat membuat tabel kontingensi yang menunjukkan frekuensi yang diamati untuk setiap kombinasi jenis kelamin dan preferensi film. Kemudian, kita dapat menghitung frekuensi yang diharapkan berdasarkan asumsi bahwa tidak ada hubungan antara variabel. Setelah itu, kita dapat menghitung statistik uji Chi-Square dan nilai p untuk menentukan apakah kita dapat menolak hipotesis nol.
Interpretasi Hasil Uji Hipotesis
| Nilai R Tabel | Interpretasi |
|---|---|
| Nilai R Tabel < Tingkat Signifikansi | Tolak hipotesis nol. Ada hubungan signifikan antara variabel. |
| Nilai R Tabel ≥ Tingkat Signifikansi | Gagal menolak hipotesis nol. Tidak ada bukti yang cukup untuk menunjukkan hubungan antara variabel. |
Kesimpulan Akhir
Dengan memahami cara menghitung R tabel, Anda dapat melakukan analisis data yang lebih kuat dan akurat. R tabel menjadi alat penting untuk menguji hipotesis dan menarik kesimpulan yang bermakna dari data penelitian Anda. Pengetahuan tentang R tabel memungkinkan Anda untuk menguji teori, memahami pola data, dan membuat keputusan yang lebih tepat berdasarkan analisis data.