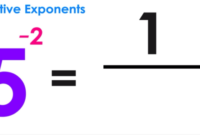Cara menghitung 1 3.3 log n – Pernahkah Anda penasaran bagaimana cara menghitung logaritma dengan basis 10 atau basis e? Mungkin Anda pernah mendengar istilah “logaritma” dalam pelajaran matematika, tapi bingung bagaimana cara menghitungnya. Jangan khawatir, menghitung logaritma tidak sesulit yang Anda bayangkan! Dalam artikel ini, kita akan membahas cara menghitung logaritma dengan kalkulator, tabel logaritma, dan program komputer. Kita juga akan menjelajahi berbagai aplikasi logaritma dalam kehidupan sehari-hari, mulai dari ilmu komputer hingga bidang ekonomi dan fisika.
Logaritma merupakan konsep matematika yang penting dalam berbagai bidang ilmu pengetahuan dan teknologi. Dengan memahami logaritma, Anda akan membuka pintu untuk memahami berbagai fenomena kompleks di sekitar kita. Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen. Dengan kata lain, logaritma adalah pangkat yang harus diberikan pada basis untuk menghasilkan bilangan tertentu. Misalnya, logaritma 100 dengan basis 10 adalah 2, karena 10 pangkat 2 sama dengan 100. Dalam notasi matematika, hal ini ditulis sebagai log10(100) = 2.
Sifat Logaritma: Cara Menghitung 1 3.3 Log N
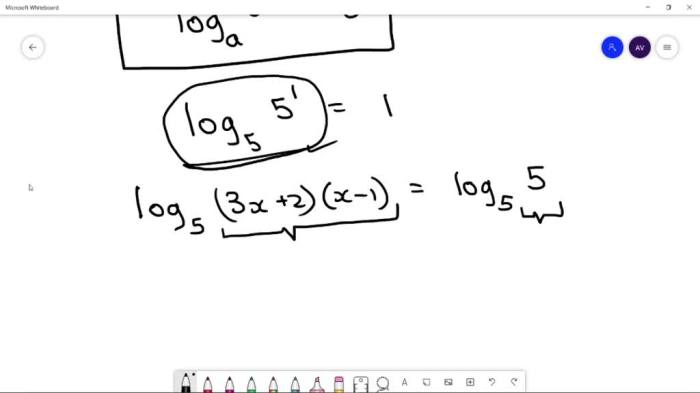
Logaritma merupakan fungsi invers dari eksponen. Artinya, jika kita memiliki persamaan eksponen ab = c, maka logaritma dari c dengan basis a adalah b. Secara matematis, kita tulis loga c = b. Sifat-sifat logaritma sangat penting dalam menyelesaikan persamaan logaritma, menyederhanakan ekspresi logaritma, dan memahami perilaku fungsi logaritma.
Sifat-Sifat Logaritma
Sifat-sifat logaritma membantu kita untuk memanipulasi dan menyelesaikan persamaan logaritma dengan lebih mudah. Berikut adalah beberapa sifat logaritma yang penting:
- loga 1 = 0: Logaritma dari 1 dengan basis apa pun selalu sama dengan 0. Hal ini karena a0 = 1 untuk setiap bilangan a yang tidak sama dengan 0.
- loga a = 1: Logaritma dari a dengan basis a selalu sama dengan 1. Hal ini karena a1 = a untuk setiap bilangan a yang tidak sama dengan 0.
- loga (b x c) = loga b + loga c: Logaritma dari perkalian dua bilangan sama dengan jumlah logaritma dari kedua bilangan tersebut.
- loga (b/c) = loga b – loga c: Logaritma dari hasil bagi dua bilangan sama dengan selisih logaritma dari kedua bilangan tersebut.
- loga bn = n loga b: Logaritma dari pangkat suatu bilangan sama dengan hasil kali pangkat dengan logaritma dari bilangan tersebut.
- loga b = logc b / logc a: Sifat ini memungkinkan kita untuk mengubah basis logaritma.
Contoh Penerapan Sifat Logaritma
Misalkan kita ingin menyelesaikan persamaan logaritma berikut: log2 (x + 1) + log2 (x – 1) = 3.
Dengan menggunakan sifat logaritma, kita dapat menyederhanakan persamaan tersebut sebagai berikut:
- log2 [(x + 1)(x – 1)] = 3 (menggunakan sifat loga (b x c) = loga b + loga c)
- log2 (x2 – 1) = 3
- 23 = x2 – 1 (mengubah persamaan logaritma ke bentuk eksponen)
- 8 = x2 – 1
- x2 = 9
- x = ±3
Namun, kita perlu memperhatikan bahwa solusi x = -3 tidak memenuhi persamaan awal karena logaritma dari bilangan negatif tidak terdefinisi. Oleh karena itu, solusi yang valid adalah x = 3.
Rumus-Rumus Terkait dengan Sifat Logaritma, Cara menghitung 1 3.3 log n
Berikut adalah beberapa rumus yang terkait dengan sifat logaritma:
| Rumus | Keterangan |
|---|---|
| loga 1 = 0 | Logaritma dari 1 dengan basis a selalu sama dengan 0. |
| loga a = 1 | Logaritma dari a dengan basis a selalu sama dengan 1. |
| loga (b x c) = loga b + loga c | Logaritma dari perkalian dua bilangan sama dengan jumlah logaritma dari kedua bilangan tersebut. |
| loga (b/c) = loga b – loga c | Logaritma dari hasil bagi dua bilangan sama dengan selisih logaritma dari kedua bilangan tersebut. |
| loga bn = n loga b | Logaritma dari pangkat suatu bilangan sama dengan hasil kali pangkat dengan logaritma dari bilangan tersebut. |
| loga b = logc b / logc a | Sifat ini memungkinkan kita untuk mengubah basis logaritma. |
Penjelasan tentang Sifat Logaritma yang Paling Sering Digunakan
Sifat logaritma yang paling sering digunakan adalah loga (b x c) = loga b + loga c dan loga bn = n loga b. Sifat pertama memungkinkan kita untuk mengubah perkalian dalam logaritma menjadi penjumlahan, sedangkan sifat kedua memungkinkan kita untuk mengubah pangkat dalam logaritma menjadi perkalian.
Cara Menghitung Logaritma
Logaritma merupakan operasi matematika yang kebalikan dari eksponen. Jika eksponen menunjukkan berapa kali suatu bilangan (basis) dikalikan dengan dirinya sendiri untuk mendapatkan hasil tertentu, maka logaritma menunjukkan pangkat berapa yang harus diberikan pada basis untuk mendapatkan hasil tersebut. Dalam artikel ini, kita akan membahas beberapa cara menghitung logaritma, mulai dari penggunaan kalkulator hingga penggunaan tabel logaritma dan program komputer.
Cara Menghitung Logaritma dengan Kalkulator
Cara termudah dan paling umum untuk menghitung logaritma adalah dengan menggunakan kalkulator. Hampir semua kalkulator ilmiah memiliki tombol logaritma (log) dan logaritma natural (ln). Untuk menghitung logaritma, Anda hanya perlu memasukkan bilangan yang ingin Anda hitung logaritmanya dan menekan tombol logaritma yang sesuai. Misalnya, untuk menghitung log 100, Anda dapat memasukkan angka 100 dan menekan tombol “log”. Hasilnya adalah 2, karena 10 pangkat 2 sama dengan 100.
Contoh Perhitungan Logaritma
Berikut adalah contoh perhitungan logaritma dengan basis 10 dan basis e (natural logarithm):
- Logaritma dengan basis 10: log 100 = 2, karena 10 pangkat 2 sama dengan 100.
- Logaritma natural (basis e): ln 2 = 0.6931, karena e pangkat 0.6931 sama dengan 2.
Cara Menghitung Logaritma dengan Tabel Logaritma
Sebelum kalkulator menjadi umum, orang-orang menggunakan tabel logaritma untuk menghitung logaritma. Tabel logaritma berisi daftar logaritma untuk berbagai bilangan dengan basis tertentu. Untuk mencari logaritma suatu bilangan, Anda dapat mencari nilai tersebut dalam tabel. Misalnya, untuk mencari log 100, Anda dapat mencari nilai 100 dalam tabel logaritma dengan basis 10. Nilai yang sesuai dengan 100 adalah 2. Jadi, log 100 = 2.
Cara Menghitung Logaritma dengan Program Komputer
Program komputer juga dapat digunakan untuk menghitung logaritma. Banyak bahasa pemrograman memiliki fungsi logaritma yang dapat Anda gunakan untuk menghitung logaritma. Misalnya, dalam bahasa Python, fungsi “math.log” dapat digunakan untuk menghitung logaritma dengan basis 10, sedangkan fungsi “math.log10” dapat digunakan untuk menghitung logaritma natural. Anda juga dapat menggunakan program kalkulator ilmiah seperti MATLAB atau Wolfram Alpha untuk menghitung logaritma.
Penutupan Akhir

Setelah memahami konsep logaritma dan berbagai sifatnya, kita dapat dengan mudah menghitung logaritma dengan berbagai metode. Baik menggunakan kalkulator, tabel logaritma, atau program komputer, menghitung logaritma menjadi lebih mudah dan praktis. Logaritma memiliki peran penting dalam berbagai bidang ilmu pengetahuan dan teknologi, dan pemahaman tentang logaritma akan membuka cakrawala baru dalam memahami dunia di sekitar kita.