Pernahkah Anda bertanya-tanya bagaimana komputer “berbicara”? Sistem bilangan biner, yang menggunakan 0 dan 1, adalah bahasa dasar komputer. Namun, bilangan biner bisa jadi rumit untuk dibaca dan ditulis, terutama untuk angka yang besar. Di sinilah bilangan oktal hadir, menawarkan representasi yang lebih ringkas dan mudah dipahami. Artikel ini akan membahas cara menghitung bilangan biner ke oktal, langkah demi langkah, dan mengungkap manfaatnya dalam dunia komputer.
Sistem bilangan oktal menggunakan angka dari 0 hingga 7, dengan setiap digit mewakili kekuatan 8. Konversi dari biner ke oktal melibatkan pengelompokan digit biner dan mengganti setiap kelompok dengan representasi oktalnya. Mari kita bahas lebih lanjut proses ini dan aplikasinya dalam dunia teknologi.
Pengertian Bilangan Biner dan Oktal: Cara Menghitung Bilangan Biner Ke Oktal
Dalam dunia komputer dan elektronik, sistem bilangan merupakan fondasi utama dalam memahami cara kerja perangkat digital. Sistem bilangan biner dan oktal adalah dua dari banyak sistem bilangan yang digunakan dalam komputasi. Masing-masing memiliki karakteristik unik yang membuatnya cocok untuk aplikasi tertentu.
Sistem Bilangan Biner
Sistem bilangan biner, atau sistem basis-2, adalah sistem bilangan yang hanya menggunakan dua digit: 0 dan 1. Setiap digit dalam sistem biner disebut bit (binary digit). Komputer menggunakan sistem biner karena mudah diimplementasikan dengan menggunakan sakelar elektronik yang dapat berada dalam dua keadaan: menyala (1) atau mati (0).
Contoh representasi angka dalam sistem biner:
- Desimal: 10, Biner: 1010
- Desimal: 5, Biner: 101
- Desimal: 20, Biner: 10100
Sistem Bilangan Oktal, Cara menghitung bilangan biner ke oktal
Sistem bilangan oktal, atau sistem basis-8, adalah sistem bilangan yang menggunakan delapan digit: 0, 1, 2, 3, 4, 5, 6, dan 7. Sistem oktal sering digunakan dalam pemrograman komputer dan dalam representasi alamat memori.
Contoh representasi angka dalam sistem oktal:
- Desimal: 10, Oktal: 12
- Desimal: 5, Oktal: 5
- Desimal: 20, Oktal: 24
Perbedaan dan Kesamaan Sistem Bilangan Biner dan Oktal
Sistem bilangan biner dan oktal memiliki beberapa perbedaan dan kesamaan. Berikut adalah perbandingannya:
| Fitur | Sistem Biner | Sistem Oktal |
|---|---|---|
| Basis | 2 | 8 |
| Digit | 0, 1 | 0, 1, 2, 3, 4, 5, 6, 7 |
| Kegunaan | Komputasi dasar, representasi data digital | Pemrograman, representasi alamat memori |
| Konversi | Mudah dikonversi ke desimal dan sebaliknya | Lebih mudah dikonversi ke desimal dan sebaliknya dibandingkan dengan biner |
Konversi Bilangan Biner ke Oktal

Konversi bilangan biner ke oktal adalah proses mengubah representasi bilangan biner (basis 2) ke representasi oktal (basis 8). Proses ini berguna dalam berbagai bidang, seperti ilmu komputer, rekayasa, dan komunikasi digital. Dalam konversi ini, kita akan mengelompokkan bilangan biner menjadi kelompok tiga digit, mulai dari digit paling kanan, dan kemudian mengganti setiap kelompok dengan nilai oktal yang setara.
Langkah-Langkah Konversi Bilangan Biner ke Oktal
Berikut langkah-langkah umum dalam mengonversi bilangan biner ke oktal:
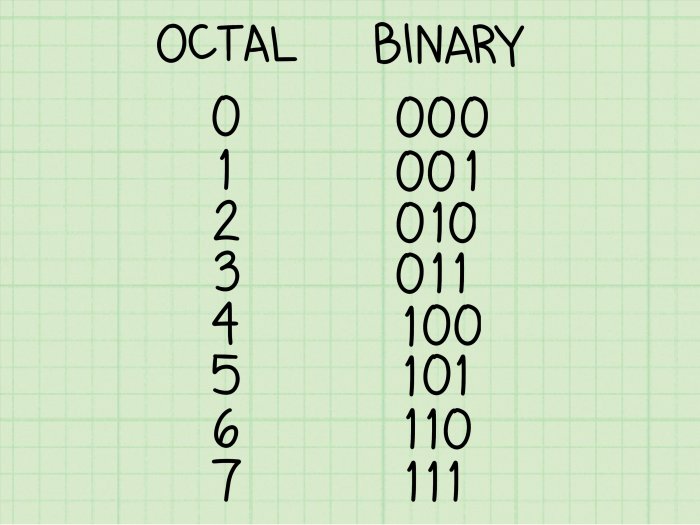
- Bagi bilangan biner menjadi kelompok tiga digit, mulai dari digit paling kanan. Jika jumlah digit tidak habis dibagi tiga, tambahkan nol di depan bilangan biner hingga jumlah digit menjadi kelipatan tiga.
- Konversi setiap kelompok tiga digit biner menjadi nilai oktal yang setara. Untuk melakukan ini, Anda dapat menggunakan tabel konversi biner-oktal atau mengingat nilai-nilai oktal yang setara untuk setiap kelompok tiga digit biner.
- Gabungkan nilai-nilai oktal yang dihasilkan untuk mendapatkan representasi oktal dari bilangan biner asli.
Contoh Konversi Bilangan Biner ke Oktal
Misalnya, kita ingin mengonversi bilangan biner 101101 ke oktal. Berikut langkah-langkahnya:
| Bilangan Biner | Kelompok Tiga Digit | Bilangan Oktal |
|---|---|---|
| 101101 | 010 110 1 | 2 6 1 |
Langkah 1: Kita bagi bilangan biner menjadi kelompok tiga digit, mulai dari digit paling kanan. Karena jumlah digit tidak habis dibagi tiga, kita tambahkan nol di depan bilangan biner, sehingga menjadi 010 110 1.
Langkah 2: Kita konversi setiap kelompok tiga digit biner menjadi nilai oktal yang setara. 010 setara dengan 2 dalam oktal, 110 setara dengan 6 dalam oktal, dan 1 setara dengan 1 dalam oktal.
Langkah 3: Kita gabungkan nilai-nilai oktal yang dihasilkan, sehingga bilangan oktal yang setara dengan 101101 adalah 261.
Aplikasi Konversi Biner ke Oktal
Konversi biner ke oktal memiliki aplikasi yang luas dalam sistem komputer dan pemrograman. Sistem bilangan oktal, yang menggunakan basis 8, sering digunakan untuk menyederhanakan representasi data biner, terutama dalam konteks seperti representasi warna, kode ASCII, dan alamat memori.
Representasi Warna
Dalam sistem komputer, warna sering direpresentasikan menggunakan sistem RGB (Red, Green, Blue). Setiap warna diwakili oleh kombinasi nilai merah, hijau, dan biru, yang berkisar dari 0 hingga 255. Setiap nilai ini dapat direpresentasikan sebagai bilangan biner 8-bit (0-255). Namun, untuk kemudahan membaca dan manipulasi, nilai-nilai ini sering diubah ke bentuk oktal. Misalnya, warna merah murni dapat diwakili sebagai (255, 0, 0) dalam sistem RGB, yang setara dengan (377, 0, 0) dalam bentuk oktal.
Kode ASCII
Kode ASCII (American Standard Code for Information Interchange) adalah standar yang digunakan untuk mewakili karakter teks dalam komputer. Setiap karakter, seperti huruf, angka, dan simbol, diwakili oleh bilangan biner 7-bit. Sistem oktal juga digunakan dalam representasi ASCII, yang menyederhanakan proses membaca dan penulisan kode karakter. Misalnya, karakter ‘A’ diwakili oleh kode biner 1000001, yang setara dengan kode oktal 101.
Alamat Memori
Alamat memori dalam komputer diwakili oleh bilangan biner. Namun, dalam beberapa kasus, alamat memori ini direpresentasikan dalam bentuk oktal untuk kemudahan pembacaan dan manipulasi. Sistem oktal digunakan dalam beberapa sistem operasi dan arsitektur komputer untuk menunjukkan alamat memori. Misalnya, alamat memori 0x1000 (dalam heksadesimal) setara dengan 4000 dalam bentuk oktal.
Keuntungan dan Kerugian
- Keuntungan:
- Efisiensi penyimpanan: Sistem oktal lebih efisien dalam penyimpanan data dibandingkan dengan sistem biner, karena setiap digit oktal mewakili tiga digit biner.
- Kemudahan membaca: Sistem oktal lebih mudah dibaca dan dipahami oleh manusia dibandingkan dengan sistem biner, karena menggunakan basis yang lebih kecil.
- Kerugian:
- Kurang umum: Sistem oktal kurang umum digunakan dibandingkan dengan sistem biner dan heksadesimal.
- Keterbatasan representasi: Sistem oktal tidak dapat mewakili semua nilai biner secara langsung, karena hanya menggunakan 8 digit.
Akhir Kata
Memahami konversi bilangan biner ke oktal membuka pintu untuk memahami cara komputer memproses dan menyimpan informasi. Dengan pengetahuan ini, Anda dapat lebih memahami sistem komputer dan pemrograman, serta menghargai efisiensi yang ditawarkan sistem oktal dalam representasi data.