Cara menghitung bilangan oktal – Pernahkah Anda mendengar tentang bilangan oktal? Sistem bilangan ini menggunakan basis 8, berbeda dengan sistem desimal yang kita gunakan sehari-hari. Bilangan oktal sering digunakan dalam dunia komputer dan teknologi informasi. Nah, dalam artikel ini, kita akan menjelajahi dunia bilangan oktal, mulai dari pengertian dasar hingga cara menghitung dan mengonversikannya.
Mempelajari cara menghitung bilangan oktal akan membuka pintu bagi Anda untuk memahami sistem bilangan yang lebih kompleks dan meningkatkan pemahaman Anda tentang cara kerja komputer. Mari kita mulai petualangan kita dalam dunia bilangan oktal!
Pengertian Bilangan Oktal
Bilangan oktal adalah sistem bilangan yang menggunakan basis 8, yang berarti hanya memiliki 8 digit berbeda, yaitu 0, 1, 2, 3, 4, 5, 6, dan 7. Sistem bilangan ini sangat penting dalam dunia komputer dan elektronik, terutama dalam pemrograman dan representasi data.
Contoh Bilangan Oktal dan Konversi ke Desimal
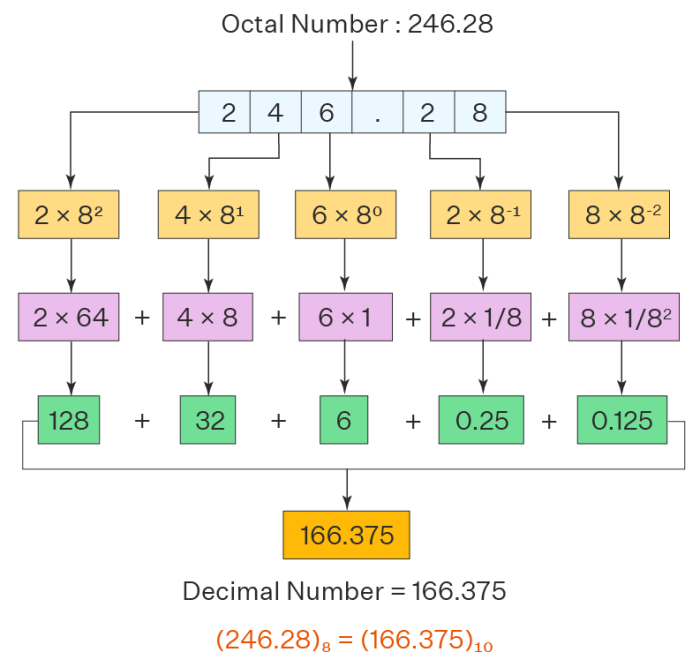
Bilangan oktal biasanya ditulis dengan awalan “0” untuk membedakannya dari bilangan desimal. Contohnya, bilangan oktal 0123 setara dengan bilangan desimal 83. Berikut adalah cara mengkonversi bilangan oktal ke desimal:
- Mulailah dari digit paling kanan bilangan oktal.
- Kalikan setiap digit dengan 8 pangkat posisi digit tersebut, dimulai dari 0 untuk digit paling kanan.
- Jumlahkan semua hasil perkalian tersebut.
Misalnya, untuk mengkonversi 0123 ke desimal:
- 3 x 80 = 3
- 2 x 81 = 16
- 1 x 82 = 64
Jumlahkan hasilnya: 3 + 16 + 64 = 83
Perbandingan Bilangan Oktal dengan Sistem Bilangan Lainnya
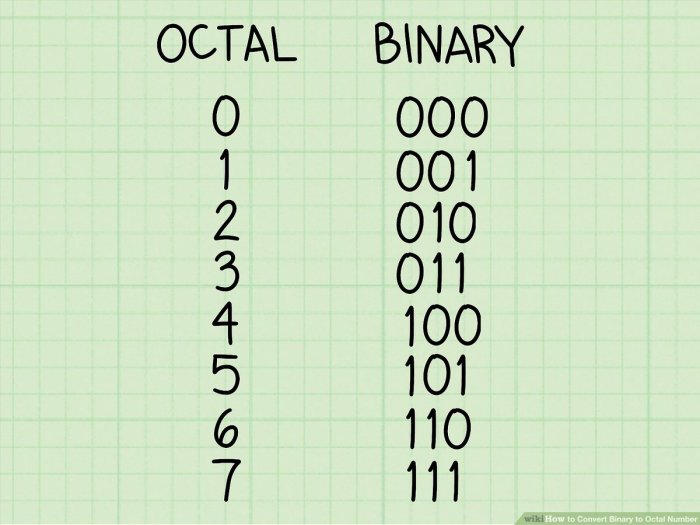
Sistem bilangan oktal, desimal, dan biner memiliki perbedaan dalam jumlah digit dan basisnya. Sistem desimal yang kita gunakan sehari-hari memiliki basis 10 dan menggunakan 10 digit (0-9). Sistem biner, yang digunakan dalam komputer, memiliki basis 2 dan hanya menggunakan 2 digit (0 dan 1).
| Sistem Bilangan | Basis | Digit |
|---|---|---|
| Desimal | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Oktal | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| Biner | 2 | 0, 1 |
Sistem bilangan oktal memiliki beberapa keunggulan dibandingkan sistem biner, yaitu lebih mudah dibaca dan ditulis, dan lebih mudah dikonversi ke desimal. Namun, sistem biner lebih efisien dalam penyimpanan dan pemrosesan data dalam komputer.
Konversi Bilangan Desimal ke Oktal
Setelah memahami cara mengkonversi bilangan oktal ke desimal, sekarang saatnya kita belajar bagaimana mengkonversi bilangan desimal ke oktal. Konversi ini melibatkan pembagian berulang dengan basis oktal (8) hingga hasil bagi menjadi 0. Sisa pembagian dari setiap langkah akan membentuk bilangan oktal yang setara.
Konversi Bilangan Desimal ke Oktal, Cara menghitung bilangan oktal
Untuk mengubah bilangan desimal ke oktal, kita perlu melakukan pembagian berulang dengan basis oktal (8). Sisa pembagian dari setiap langkah akan membentuk bilangan oktal yang setara. Berikut langkah-langkahnya:
- Bagi bilangan desimal dengan 8.
- Catat sisa pembagian. Sisa ini adalah digit pertama bilangan oktal.
- Bagi hasil bagi dari langkah sebelumnya dengan 8.
- Catat sisa pembagian. Sisa ini adalah digit kedua bilangan oktal.
- Ulangi langkah 3 dan 4 sampai hasil bagi menjadi 0.
- Tulis sisa pembagian yang didapat dari setiap langkah, dimulai dari sisa terakhir hingga sisa pertama. Ini adalah bilangan oktal yang setara dengan bilangan desimal awal.
Contoh Konversi Bilangan Desimal ke Oktal
Misalnya, kita ingin mengkonversi bilangan desimal 25 ke oktal. Berikut langkah-langkahnya:
| Langkah | Pembagian | Hasil Bagi | Sisa |
|---|---|---|---|
| 1 | 25 / 8 | 3 | 1 |
| 2 | 3 / 8 | 0 | 3 |
Sisa pembagian yang didapat adalah 3 dan 1. Jadi, bilangan oktal yang setara dengan bilangan desimal 25 adalah 318.
Aplikasi Bilangan Oktal: Cara Menghitung Bilangan Oktal
Bilangan oktal, meskipun mungkin tidak sepopuler sistem bilangan desimal atau biner, memiliki peran penting dalam berbagai bidang. Penggunaan bilangan oktal terutama terfokus pada sistem komputer dan teknologi informasi, dan juga merambah ke bidang sistem kontrol.
Komputer dan Teknologi Informasi
Dalam dunia komputer dan teknologi informasi, bilangan oktal memiliki beberapa aplikasi penting, terutama pada masa awal perkembangan komputer.
- Representasi Data: Pada masa awal, beberapa komputer menggunakan bilangan oktal untuk merepresentasikan data. Sistem ini memudahkan programmer untuk mengingat dan mengoperasikan data dalam bentuk yang lebih ringkas dibandingkan dengan sistem biner.
- Perintah Mesin: Beberapa arsitektur komputer menggunakan bilangan oktal untuk menyatakan perintah mesin. Contohnya, sistem operasi UNIX awal menggunakan bilangan oktal untuk menyatakan izin akses file.
- Perangkat Lunak: Beberapa bahasa pemrograman awal, seperti C dan Assembly, mendukung penggunaan bilangan oktal. Meskipun penggunaannya semakin berkurang dengan perkembangan teknologi, bilangan oktal masih digunakan dalam beberapa aplikasi tertentu, terutama dalam konteks sistem embedded.
Sistem Kontrol
Bilangan oktal juga memiliki peran penting dalam sistem kontrol, terutama dalam konteks pemrograman mikrokontroler dan sistem digital.
- Pemrograman Mikrokontroler: Beberapa mikrokontroler menggunakan bilangan oktal dalam sistem pemrogramannya. Hal ini memudahkan programmer untuk menyatakan alamat memori, register, dan perintah yang dibutuhkan dalam sistem mikrokontroler.
- Sistem Digital: Bilangan oktal digunakan dalam sistem digital untuk merepresentasikan data dan menjalankan operasi logika. Contohnya, bilangan oktal digunakan dalam sistem kontrol industri untuk menentukan status peralatan dan menjalankan perintah kontrol.
Contoh Aplikasi Bilangan Oktal
Sebagai contoh, dalam sistem operasi UNIX, izin akses file direpresentasikan menggunakan bilangan oktal. Angka oktal “755” menyatakan bahwa pemilik file memiliki hak baca, tulis, dan eksekusi, sedangkan pengguna lain hanya memiliki hak baca dan eksekusi.
Contoh lain, dalam pemrograman mikrokontroler, bilangan oktal digunakan untuk menyatakan alamat memori dan register. Misalnya, alamat memori “0x20” dalam sistem desimal setara dengan alamat “040” dalam sistem oktal.
Pemungkas

Dengan memahami cara menghitung bilangan oktal, Anda akan memiliki kemampuan yang lebih luas dalam memahami sistem bilangan dan penerapannya dalam berbagai bidang. Mulailah dengan mempelajari dasar-dasarnya, berlatih dengan contoh-contoh, dan jangan takut untuk mengeksplorasi lebih jauh. Selamat belajar dan semoga sukses!