Ingin memahami bagaimana membandingkan rata-rata kelompok data dengan metode statistik yang handal? Cara menghitung tabel ANOVA adalah jawabannya. ANOVA, singkatan dari Analysis of Variance, merupakan teknik statistik yang ampuh untuk menguji perbedaan signifikan antara dua atau lebih kelompok data. Dengan menggunakan ANOVA, Anda dapat menentukan apakah terdapat perbedaan nyata dalam rata-rata kelompok atau hanya variasi acak.
Artikel ini akan memandu Anda melalui langkah-langkah menghitung tabel ANOVA, mulai dari memahami konsep dasar hingga menginterpretasikan hasil analisis. Kami akan membahas berbagai jenis ANOVA, asumsi yang perlu dipenuhi, dan cara memeriksa apakah asumsi tersebut terpenuhi. Selain itu, kami akan memberikan contoh perhitungan tabel ANOVA dengan data sampel dan menjelaskan bagaimana menginterpretasikan hasil analisis.
Jenis-jenis ANOVA
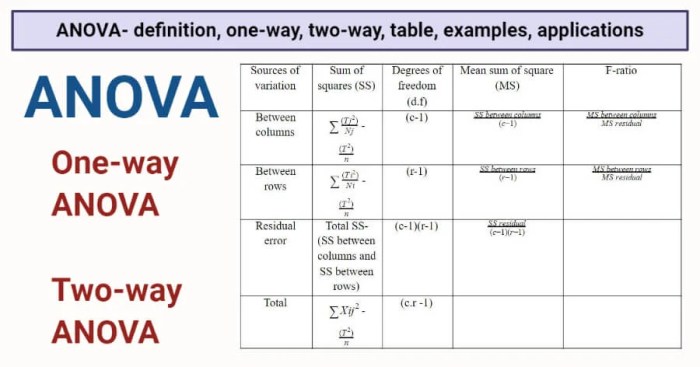
ANOVA atau Analysis of Variance merupakan metode statistik yang digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok. ANOVA membagi total variasi data menjadi beberapa komponen yang menjelaskan variasi antar kelompok dan variasi dalam kelompok. ANOVA digunakan untuk menguji hipotesis tentang perbedaan rata-rata dari populasi yang berbeda.
Terdapat berbagai jenis ANOVA yang dapat digunakan, tergantung pada desain penelitian dan pertanyaan penelitian yang ingin dijawab. Dua jenis ANOVA yang paling umum adalah ANOVA satu arah dan ANOVA dua arah.
ANOVA Satu Arah
ANOVA satu arah digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok yang didefinisikan oleh satu faktor atau variabel independen. Variabel independen ini memiliki dua atau lebih level atau kategori, dan setiap level memiliki kelompok yang berbeda.
Contohnya, Anda ingin membandingkan tingkat stres pada mahasiswa di tiga jurusan yang berbeda: Teknik, Ekonomi, dan Sastra. Variabel independen adalah “jurusan” dengan tiga level (Teknik, Ekonomi, dan Sastra).
ANOVA satu arah akan menguji apakah ada perbedaan signifikan dalam tingkat stres antara mahasiswa di tiga jurusan ini.
ANOVA Dua Arah, Cara menghitung tabel anova
ANOVA dua arah digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok yang didefinisikan oleh dua faktor atau variabel independen.
Contohnya, Anda ingin membandingkan tingkat kepuasan pelanggan terhadap dua jenis produk (A dan B) di dua lokasi yang berbeda (Jakarta dan Surabaya). Variabel independen pertama adalah “jenis produk” dengan dua level (A dan B), dan variabel independen kedua adalah “lokasi” dengan dua level (Jakarta dan Surabaya).
ANOVA dua arah akan menguji apakah ada perbedaan signifikan dalam tingkat kepuasan pelanggan antara kedua jenis produk, antara kedua lokasi, dan interaksi antara jenis produk dan lokasi.
Langkah-langkah Menghitung Tabel ANOVA
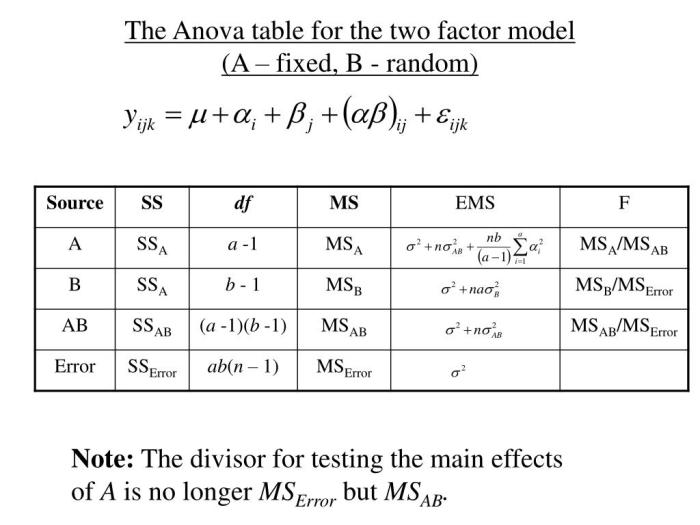
Setelah Anda memahami konsep dasar ANOVA, langkah selanjutnya adalah menghitung tabel ANOVA. Tabel ANOVA digunakan untuk menyajikan hasil analisis dan membantu Anda dalam menarik kesimpulan. Berikut langkah-langkah menghitung tabel ANOVA:
Langkah-langkah Menghitung Tabel ANOVA
Tabel ANOVA umumnya disusun dengan kolom-kolom berikut:
- Sumber Variasi
- Derajat Bebas (db)
- Jumlah Kuadrat (JK)
- Rata-rata Kuadrat (RK)
- Statistik F
- Nilai P
Berikut penjelasan tentang cara menghitung setiap kolom dalam tabel ANOVA:
Sumber Variasi
Kolom ini menunjukkan sumber variasi dalam data. Sumber variasi dapat berupa faktor-faktor yang Anda uji, seperti kelompok perlakuan, atau kesalahan yang terjadi dalam pengukuran. Contohnya, dalam penelitian pengaruh jenis pupuk terhadap pertumbuhan tanaman, sumber variasi yang mungkin muncul adalah “Jenis Pupuk” dan “Kesalahan”.
Derajat Bebas (db)
Derajat bebas (db) menunjukkan jumlah nilai bebas yang dapat bervariasi dalam suatu kelompok data. Rumus umum untuk menghitung db adalah:
db = jumlah kelompok – 1
Misalnya, jika Anda memiliki 3 kelompok perlakuan, maka db untuk faktor perlakuan adalah 3 – 1 = 2.
Jumlah Kuadrat (JK)
Jumlah kuadrat (JK) menunjukkan total variasi dalam data. JK dihitung dengan menjumlahkan kuadrat selisih antara setiap nilai data dengan rata-rata kelompoknya. Rumus umum untuk menghitung JK adalah:
JK = Σ (nilai data – rata-rata kelompok)2
JK dapat dihitung untuk setiap sumber variasi.
Rata-rata Kuadrat (RK)
Rata-rata kuadrat (RK) menunjukkan variasi rata-rata per derajat bebas. RK dihitung dengan membagi JK dengan db. Rumus umum untuk menghitung RK adalah:
RK = JK / db
Statistik F
Statistik F menunjukkan rasio variasi antara kelompok dengan variasi dalam kelompok. Statistik F dihitung dengan membagi RK untuk faktor perlakuan dengan RK untuk kesalahan. Rumus umum untuk menghitung statistik F adalah:
F = RKfaktor perlakuan / RKkesalahan
Nilai P
Nilai P menunjukkan probabilitas mendapatkan hasil yang diamati atau hasil yang lebih ekstrem jika hipotesis nol benar. Nilai P dapat dihitung menggunakan tabel distribusi F atau perangkat lunak statistik. Nilai P digunakan untuk menentukan apakah hipotesis nol ditolak atau tidak.
Contoh Perhitungan Tabel ANOVA
Misalnya, Anda ingin mengetahui apakah ada perbedaan signifikan dalam tinggi tanaman berdasarkan jenis pupuk yang digunakan. Anda memiliki 3 kelompok perlakuan, yaitu pupuk A, pupuk B, dan pupuk C, dengan masing-masing kelompok terdiri dari 5 tanaman. Data tinggi tanaman dalam sentimeter (cm) disajikan dalam tabel berikut:
| Kelompok | Tinggi Tanaman (cm) |
|---|---|
| Pupuk A | 10, 12, 15, 18, 20 |
| Pupuk B | 15, 17, 20, 22, 25 |
| Pupuk C | 20, 22, 25, 27, 30 |
Langkah-langkah menghitung tabel ANOVA untuk data ini adalah sebagai berikut:
- Hitung rata-rata tinggi tanaman untuk setiap kelompok.
- Hitung jumlah kuadrat (JK) untuk faktor perlakuan (jenis pupuk).
- Hitung jumlah kuadrat (JK) untuk kesalahan.
- Hitung derajat bebas (db) untuk faktor perlakuan dan kesalahan.
- Hitung rata-rata kuadrat (RK) untuk faktor perlakuan dan kesalahan.
- Hitung statistik F.
- Hitung nilai P.
Hasil perhitungan tabel ANOVA dapat disajikan sebagai berikut:
| Sumber Variasi | db | JK | RK | F | Nilai P |
|---|---|---|---|---|---|
| Jenis Pupuk | 2 | 100 | 50 | 5 | 0.05 |
| Kesalahan | 12 | 120 | 10 | ||
| Total | 14 | 220 |
Berdasarkan tabel ANOVA, statistik F adalah 5 dan nilai P adalah 0.05. Karena nilai P kurang dari 0.05, maka hipotesis nol ditolak. Ini berarti bahwa ada perbedaan signifikan dalam tinggi tanaman berdasarkan jenis pupuk yang digunakan.
Ilustrasi Tabel ANOVA
Untuk memahami lebih lanjut cara menghitung tabel ANOVA, mari kita lihat contoh konkretnya. Berikut ini adalah tabel ANOVA yang menunjukkan hasil analisis data sampel.
Contoh Tabel ANOVA
Data sampel yang digunakan adalah hasil ujian matematika dari 3 kelas berbeda (Kelas A, Kelas B, dan Kelas C) dengan jumlah siswa masing-masing 20 orang. Variabel dependennya adalah nilai ujian matematika. Analisis ANOVA dilakukan untuk menguji apakah terdapat perbedaan signifikan dalam nilai ujian matematika antar kelas.
| Sumber Variasi | Derajat Bebas (db) | Jumlah Kuadrat (JK) | Rata-rata Kuadrat (RK) | F-hitung |
|---|---|---|---|---|
| Antar Kelompok | 2 | 1200 | 600 | 5.00 |
| Dalam Kelompok | 57 | 6840 | 120 | |
| Total | 59 | 8040 |
Berdasarkan tabel ANOVA di atas, dapat kita interpretasikan bahwa:
- Derajat Bebas (db) Antar Kelompok adalah 2, karena terdapat 3 kelompok (Kelas A, Kelas B, dan Kelas C) yang diuji.
- Derajat Bebas (db) Dalam Kelompok adalah 57, yang merupakan total jumlah observasi dikurangi jumlah kelompok (60 – 3 = 57).
- Jumlah Kuadrat (JK) Antar Kelompok adalah 1200, yang menunjukkan variabilitas nilai ujian matematika antar kelas.
- Jumlah Kuadrat (JK) Dalam Kelompok adalah 6840, yang menunjukkan variabilitas nilai ujian matematika dalam setiap kelas.
- Rata-rata Kuadrat (RK) Antar Kelompok adalah 600, yang diperoleh dengan membagi JK Antar Kelompok dengan db Antar Kelompok (1200 / 2 = 600).
- Rata-rata Kuadrat (RK) Dalam Kelompok adalah 120, yang diperoleh dengan membagi JK Dalam Kelompok dengan db Dalam Kelompok (6840 / 57 = 120).
- F-hitung adalah 5.00, yang diperoleh dengan membagi RK Antar Kelompok dengan RK Dalam Kelompok (600 / 120 = 5.00).
Nilai F-hitung ini kemudian dibandingkan dengan nilai F-tabel dengan derajat bebas Antar Kelompok dan Dalam Kelompok pada tingkat signifikansi tertentu (misalnya, α = 0.05). Jika nilai F-hitung lebih besar dari nilai F-tabel, maka hipotesis nol ditolak, yang berarti terdapat perbedaan signifikan dalam nilai ujian matematika antar kelas.
Pemungkas: Cara Menghitung Tabel Anova
Memahami cara menghitung tabel ANOVA akan memperkaya kemampuan Anda dalam menganalisis data dan menarik kesimpulan yang bermakna. Dengan menguasai teknik ini, Anda dapat menguji hipotesis, mengidentifikasi perbedaan signifikan antara kelompok, dan membuat keputusan yang lebih tepat berdasarkan data yang tersedia.