Menilai kemampuan siswa dalam memecahkan masalah matematika melalui soal essay bisa menjadi tantangan tersendiri bagi guru. Bagaimana memastikan penilaian objektif dan adil? Di sinilah rubrik penilaian berperan penting. Contoh Rubrik Penilaian Soal Essay Matematika: Panduan Lengkap untuk Guru akan membantu Anda memahami cara merancang dan menggunakan rubrik penilaian yang efektif untuk soal essay matematika.
Rubrik penilaian merupakan alat bantu yang sistematis dan terstruktur untuk menilai kualitas jawaban siswa pada soal essay. Dengan rubrik, penilaian menjadi lebih objektif, adil, dan transparan. Artikel ini akan membahas pengertian rubrik, komponen-komponennya, aspek penilaian, contoh rubrik untuk berbagai tingkat kesulitan, serta keuntungan dan kerugian penggunaannya.
Pengertian Rubrik Penilaian Soal Essay Matematika
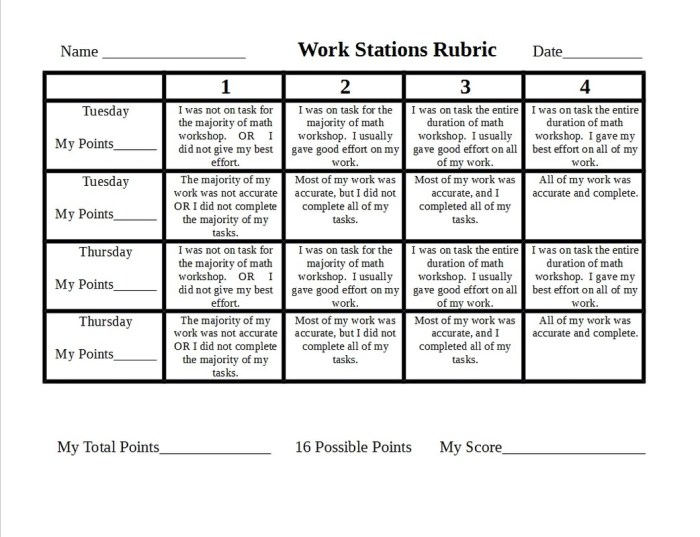
Rubrik penilaian soal essay matematika adalah alat yang digunakan untuk menilai jawaban siswa secara objektif dan sistematis. Rubrik ini berisi kriteria yang jelas dan terstruktur untuk menilai setiap aspek jawaban siswa, sehingga proses penilaian menjadi lebih adil dan konsisten.
Tujuan Penggunaan Rubrik Penilaian Soal Essay Matematika
Penggunaan rubrik penilaian soal essay matematika memiliki beberapa tujuan penting, antara lain:
- Meningkatkan objektivitas dan konsistensi penilaian. Dengan kriteria yang jelas, rubrik membantu guru menilai jawaban siswa secara adil dan konsisten, terlepas dari subjektivitas guru.
- Memudahkan proses penilaian. Rubrik memberikan panduan yang jelas untuk menilai setiap aspek jawaban, sehingga proses penilaian menjadi lebih mudah dan efisien.
- Memberikan umpan balik yang lebih spesifik. Rubrik membantu guru memberikan umpan balik yang lebih spesifik kepada siswa, sehingga siswa dapat memahami kekurangan dan kelebihan dalam jawaban mereka.
- Meningkatkan motivasi belajar siswa. Dengan rubrik, siswa dapat mengetahui kriteria yang digunakan untuk menilai jawaban mereka, sehingga mereka termotivasi untuk belajar lebih baik dan mencapai skor yang lebih tinggi.
Contoh Rubrik Penilaian Soal Essay Matematika Sederhana
Berikut adalah contoh rubrik penilaian soal essay matematika sederhana dengan 3 aspek penilaian:
| Aspek Penilaian | Deskripsi | Skor | Contoh Jawaban |
|---|---|---|---|
| Pemahaman Konsep | Siswa menunjukkan pemahaman yang benar tentang konsep matematika yang diuji dalam soal. | 4 | Siswa mampu menjelaskan konsep dengan benar dan memberikan contoh yang tepat. |
| Proses Penyelesaian | Siswa menunjukkan langkah-langkah penyelesaian yang benar dan sistematis. | 3 | Siswa menunjukkan langkah-langkah penyelesaian yang benar dan lengkap, tetapi ada sedikit kesalahan dalam perhitungan. |
| Presentasi Jawaban | Siswa menyajikan jawaban dengan jelas, terstruktur, dan mudah dipahami. | 2 | Siswa menyajikan jawaban dengan cukup jelas, tetapi struktur jawaban kurang terorganisir. |
Komponen Rubrik Penilaian Soal Essay Matematika
Merancang rubrik penilaian soal essay matematika bukan sekadar membuat daftar kriteria, tetapi lebih dari itu, merupakan proses sistematis untuk memastikan penilaian yang adil, objektif, dan transparan. Rubrik yang baik membantu guru dalam menilai jawaban siswa secara terstruktur, memberikan feedback yang konstruktif, dan mendorong pembelajaran yang lebih mendalam. Untuk mencapai tujuan tersebut, terdapat beberapa komponen utama yang perlu dipertimbangkan dalam merancang rubrik penilaian soal essay matematika.
Kriteria Penilaian
Kriteria penilaian merupakan jantung dari rubrik, yang mendefinisikan aspek-aspek penting yang ingin dinilai dalam jawaban siswa. Kriteria ini harus dirumuskan dengan jelas dan spesifik, sehingga guru dan siswa sama-sama memahami apa yang diharapkan dalam jawaban essay.
- Pemahaman Konsep: Menilai seberapa baik siswa memahami konsep matematika yang diujikan dalam soal essay. Contohnya, dalam soal tentang persamaan linear, kriteria ini akan menilai apakah siswa mampu mendefinisikan persamaan linear, mengidentifikasi variabel dan konstanta, serta menerapkan rumus yang tepat.
- Kemampuan Menalar: Menilai seberapa baik siswa mampu berpikir logis dan menghubungkan konsep matematika dengan masalah yang diberikan dalam soal. Contohnya, dalam soal tentang geometri, kriteria ini akan menilai apakah siswa mampu menganalisis bentuk geometri, menemukan hubungan antar sudut dan sisi, serta menerapkan teorema yang relevan.
- Kejelasan Penyelesaian: Menilai seberapa baik siswa mampu menyajikan solusi dalam bentuk langkah-langkah yang terstruktur, logis, dan mudah dipahami. Contohnya, dalam soal tentang aljabar, kriteria ini akan menilai apakah siswa mampu menunjukkan langkah-langkah penyelesaian yang sistematis, menggunakan simbol matematika yang tepat, dan menuliskan jawaban akhir dengan jelas.
- Keakuratan Jawaban: Menilai seberapa benar jawaban siswa berdasarkan konsep matematika yang diujikan. Contohnya, dalam soal tentang statistika, kriteria ini akan menilai apakah siswa mampu menghitung data statistik dengan benar, menggunakan rumus yang tepat, dan mendapatkan hasil yang akurat.
Tingkat Pencapaian
Tingkat pencapaian menggambarkan skala penilaian yang digunakan untuk mengukur kinerja siswa terhadap kriteria yang telah ditetapkan. Skala ini biasanya menggunakan rentang nilai atau deskripsi verbal yang menunjukkan tingkat penguasaan siswa terhadap konsep matematika yang diujikan.
- Sangat Baik: Menunjukkan pemahaman yang mendalam tentang konsep, kemampuan menalar yang kuat, penyelesaian yang terstruktur dan akurat, dan jawaban yang benar.
- Baik: Menunjukkan pemahaman yang cukup baik tentang konsep, kemampuan menalar yang baik, penyelesaian yang terstruktur, dan jawaban yang sebagian besar benar.
- Cukup: Menunjukkan pemahaman yang terbatas tentang konsep, kemampuan menalar yang kurang kuat, penyelesaian yang kurang terstruktur, dan jawaban yang sebagian benar.
- Kurang: Menunjukkan pemahaman yang sangat terbatas tentang konsep, kemampuan menalar yang lemah, penyelesaian yang tidak terstruktur, dan jawaban yang sebagian besar salah.
Skor Poin
Skor poin digunakan untuk memberikan nilai numerik pada setiap tingkat pencapaian dalam rubrik. Skor poin ini memudahkan guru dalam memberikan nilai akhir untuk jawaban essay siswa.
- Sangat Baik: 4 poin
- Baik: 3 poin
- Cukup: 2 poin
- Kurang: 1 poin
Contoh Penerapan Rubrik
| Komponen Rubrik | Deskripsi | Contoh Penerapan |
|---|---|---|
| Pemahaman Konsep | Siswa mampu mendefinisikan persamaan linear dan mengidentifikasi variabel dan konstanta. | Siswa mampu menuliskan definisi persamaan linear dengan benar, yaitu persamaan yang memiliki variabel dengan pangkat tertinggi 1. Siswa juga mampu mengidentifikasi variabel x dan y serta konstanta 2 dalam persamaan 2x + y = 5. |
| Kemampuan Menalar | Siswa mampu menggunakan persamaan linear untuk menyelesaikan masalah kontekstual. | Siswa mampu menerjemahkan masalah kontekstual tentang jumlah buah apel dan jeruk ke dalam persamaan linear, dan kemudian menyelesaikan persamaan tersebut untuk menemukan jumlah masing-masing buah. |
| Kejelasan Penyelesaian | Siswa menunjukkan langkah-langkah penyelesaian yang sistematis dan mudah dipahami. | Siswa menuliskan langkah-langkah penyelesaian persamaan linear dengan menggunakan simbol matematika yang tepat dan mencantumkan setiap langkah dengan jelas. |
| Keakuratan Jawaban | Siswa mendapatkan jawaban yang benar berdasarkan konsep persamaan linear. | Siswa mampu menyelesaikan persamaan linear dan mendapatkan nilai x dan y yang benar. |
Aspek Penilaian Soal Essay Matematika
Menilai soal essay matematika tidak hanya sebatas melihat jawaban benar atau salah. Ada berbagai aspek yang perlu diperhatikan untuk menilai pemahaman siswa terhadap konsep matematika, kemampuan mereka dalam menyelesaikan masalah, dan kemampuan mereka dalam mengkomunikasikan solusi secara logis dan sistematis.
Aspek Penilaian Soal Essay Matematika
Beberapa aspek penilaian yang relevan untuk menilai soal essay matematika adalah:
- Ketepatan Konsep: Aspek ini menilai sejauh mana siswa memahami konsep matematika yang diujikan dalam soal. Siswa harus mampu menerapkan konsep yang benar dalam menyelesaikan soal dan menunjukkan pemahaman yang mendalam tentang konsep tersebut.
- Kejelasan Langkah Penyelesaian: Aspek ini menilai kemampuan siswa dalam menunjukkan langkah-langkah penyelesaian soal secara logis dan sistematis. Siswa harus mampu menuliskan setiap langkah penyelesaian dengan jelas dan mudah dipahami, serta menunjukkan bagaimana setiap langkah berhubungan dengan langkah sebelumnya.
- Keakuratan Perhitungan: Aspek ini menilai kemampuan siswa dalam melakukan perhitungan matematika dengan benar. Siswa harus mampu melakukan perhitungan dengan teliti dan akurat, menghindari kesalahan hitung yang dapat mempengaruhi hasil akhir.
- Kemampuan Menginterpretasikan Hasil: Aspek ini menilai kemampuan siswa dalam menginterpretasikan hasil yang diperoleh dari penyelesaian soal. Siswa harus mampu menjelaskan makna dari hasil yang diperoleh dan menghubungkannya dengan konteks soal.
Contoh Soal Essay dan Rubrik Penilaian
Berikut adalah contoh soal essay matematika dan rubrik penilaian yang sesuai dengan aspek-aspek penilaian yang telah ditentukan:
Soal Essay
Sebuah taman berbentuk persegi panjang dengan panjang 12 meter dan lebar 8 meter. Di dalam taman tersebut akan dibuat kolam berbentuk lingkaran dengan diameter 4 meter. Hitunglah luas taman yang tersisa setelah kolam dibuat!
Rubrik Penilaian
| Aspek Penilaian | Skor | Keterangan |
|---|---|---|
| Ketepatan Konsep | 4 | Siswa mampu menerapkan konsep luas persegi panjang dan luas lingkaran dengan benar. |
| 3 | Siswa mampu menerapkan salah satu konsep dengan benar, tetapi salah satu konsep lainnya tidak tepat. | |
| 2 | Siswa mampu menerapkan kedua konsep, tetapi dengan kesalahan konsep yang signifikan. | |
| 1 | Siswa tidak mampu menerapkan konsep yang benar. | |
| Kejelasan Langkah Penyelesaian | 4 | Siswa mampu menunjukkan langkah-langkah penyelesaian secara logis dan sistematis. |
| 3 | Siswa mampu menunjukkan langkah-langkah penyelesaian, tetapi kurang logis atau sistematis. | |
| 2 | Siswa menunjukkan langkah-langkah penyelesaian yang tidak lengkap atau tidak jelas. | |
| 1 | Siswa tidak mampu menunjukkan langkah-langkah penyelesaian. | |
| Keakuratan Perhitungan | 4 | Siswa mampu melakukan perhitungan dengan benar dan akurat. |
| 3 | Siswa melakukan perhitungan dengan sedikit kesalahan. | |
| 2 | Siswa melakukan perhitungan dengan banyak kesalahan. | |
| 1 | Siswa tidak mampu melakukan perhitungan dengan benar. | |
| Kemampuan Menginterpretasikan Hasil | 4 | Siswa mampu menginterpretasikan hasil yang diperoleh dengan benar dan menghubungkannya dengan konteks soal. |
| 3 | Siswa mampu menginterpretasikan hasil, tetapi kurang tepat dalam menghubungkannya dengan konteks soal. | |
| 2 | Siswa tidak mampu menginterpretasikan hasil dengan benar. | |
| 1 | Siswa tidak mampu menginterpretasikan hasil dan tidak menghubungkannya dengan konteks soal. |
Contoh Jawaban Soal Essay
Berikut adalah contoh jawaban soal essay dan skor yang diberikan berdasarkan rubrik penilaian:
Jawaban Siswa
Luas taman = panjang x lebar = 12 meter x 8 meter = 96 meter2. Luas kolam = πr2 = π(2 meter)2 = 4π meter2. Luas taman yang tersisa = Luas taman – Luas kolam = 96 meter2 – 4π meter2 = (96 – 4π) meter2. Jadi, luas taman yang tersisa adalah (96 – 4π) meter2.
Skor
Berdasarkan rubrik penilaian, jawaban siswa tersebut mendapatkan skor sebagai berikut:
- Ketepatan Konsep: 4 (Siswa mampu menerapkan konsep luas persegi panjang dan luas lingkaran dengan benar.)
- Kejelasan Langkah Penyelesaian: 4 (Siswa mampu menunjukkan langkah-langkah penyelesaian secara logis dan sistematis.)
- Keakuratan Perhitungan: 4 (Siswa mampu melakukan perhitungan dengan benar dan akurat.)
- Kemampuan Menginterpretasikan Hasil: 4 (Siswa mampu menginterpretasikan hasil yang diperoleh dengan benar dan menghubungkannya dengan konteks soal.)
Total skor yang diperoleh siswa adalah 16.
Contoh Rubrik Penilaian Soal Essay Matematika Berbagai Tingkat Kesulitan
Rubrik penilaian soal essay matematika merupakan panduan yang membantu guru dalam menilai jawaban siswa secara objektif dan adil. Rubrik ini memberikan kriteria penilaian yang jelas dan terstruktur, sehingga memudahkan guru dalam memberikan skor yang konsisten untuk setiap jawaban siswa.
Contoh Rubrik Penilaian Soal Essay Matematika Berbagai Tingkat Kesulitan
Untuk membuat rubrik penilaian soal essay matematika yang efektif, perlu mempertimbangkan tingkat kesulitan soal. Tingkat kesulitan soal dapat dibedakan menjadi tiga kategori: mudah, sedang, dan sulit. Berikut adalah contoh rubrik penilaian untuk soal essay matematika dengan tingkat kesulitan yang berbeda:
Soal Essay Tingkat Kesulitan Mudah
Soal essay tingkat kesulitan mudah biasanya menuntut siswa untuk mengaplikasikan konsep dasar matematika yang telah dipelajari. Soal ini biasanya berbentuk soal yang menanyakan definisi, rumus, atau langkah-langkah dalam menyelesaikan suatu masalah. Contoh soal essay tingkat kesulitan mudah:
Jelaskan pengertian persamaan linear satu variabel dan berikan contohnya!
Rubrik Penilaian Soal Essay Tingkat Kesulitan Mudah
| Kriteria | Skor | Keterangan |
|---|---|---|
| Pengertian persamaan linear satu variabel | 2 | Siswa dapat menjelaskan pengertian persamaan linear satu variabel dengan benar dan tepat. |
| Contoh persamaan linear satu variabel | 2 | Siswa dapat memberikan contoh persamaan linear satu variabel yang benar. |
| Kejelasan dan kelengkapan jawaban | 1 | Jawaban siswa ditulis dengan jelas, runtut, dan lengkap. |
| Total Skor | 5 |
Soal Essay Tingkat Kesulitan Sedang
Soal essay tingkat kesulitan sedang menuntut siswa untuk mengaplikasikan konsep matematika yang lebih kompleks dan memadukan beberapa konsep dalam menyelesaikan suatu masalah. Soal ini biasanya berbentuk soal yang menanyakan langkah-langkah penyelesaian suatu masalah atau analisis suatu data. Contoh soal essay tingkat kesulitan sedang:
Hitunglah luas segitiga ABC dengan titik A (2, 3), B (5, 1), dan C (1, 0)!
Rubrik Penilaian Soal Essay Tingkat Kesulitan Sedang
| Kriteria | Skor | Keterangan |
|---|---|---|
| Rumus luas segitiga | 2 | Siswa dapat menuliskan rumus luas segitiga dengan benar. |
| Langkah-langkah perhitungan | 2 | Siswa dapat menunjukkan langkah-langkah perhitungan luas segitiga dengan benar dan tepat. |
| Hasil perhitungan | 1 | Siswa mendapatkan hasil perhitungan luas segitiga yang benar. |
| Kejelasan dan kelengkapan jawaban | 1 | Jawaban siswa ditulis dengan jelas, runtut, dan lengkap. |
| Total Skor | 6 |
Soal Essay Tingkat Kesulitan Sulit
Soal essay tingkat kesulitan sulit menuntut siswa untuk mengaplikasikan konsep matematika yang lebih kompleks dan memadukan beberapa konsep dalam menyelesaikan suatu masalah yang kompleks. Soal ini biasanya berbentuk soal yang menanyakan pembuktian teorema, analisis data yang kompleks, atau penerapan konsep matematika dalam kehidupan nyata. Contoh soal essay tingkat kesulitan sulit:
Buktikan bahwa jumlah sudut-sudut dalam segitiga adalah 180 derajat!
Rubrik Penilaian Soal Essay Tingkat Kesulitan Sulit
| Kriteria | Skor | Keterangan |
|---|---|---|
| Langkah-langkah pembuktian | 3 | Siswa dapat menunjukkan langkah-langkah pembuktian teorema dengan benar dan tepat. |
| Logika pembuktian | 2 | Siswa dapat menunjukkan logika pembuktian yang benar dan konsisten. |
| Kesimpulan pembuktian | 1 | Siswa dapat menarik kesimpulan pembuktian yang benar dan tepat. |
| Kejelasan dan kelengkapan jawaban | 1 | Jawaban siswa ditulis dengan jelas, runtut, dan lengkap. |
| Total Skor | 7 |
Perbedaan Karakteristik dan Kriteria Penilaian pada Setiap Tingkat Kesulitan
Perbedaan karakteristik dan kriteria penilaian pada setiap tingkat kesulitan terletak pada kompleksitas konsep matematika yang diuji, tingkat pemahaman yang diharapkan, dan kedalaman analisis yang dibutuhkan dalam menjawab soal.
- Soal essay tingkat kesulitan mudah biasanya menguji pemahaman konsep dasar dan kemampuan siswa dalam mengaplikasikannya secara sederhana. Kriteria penilaian lebih fokus pada pemahaman konsep, keakuratan jawaban, dan kejelasan penyampaian.
- Soal essay tingkat kesulitan sedang menguji kemampuan siswa dalam mengaplikasikan konsep matematika yang lebih kompleks dan memadukan beberapa konsep dalam menyelesaikan suatu masalah. Kriteria penilaian lebih fokus pada pemahaman konsep, keakuratan jawaban, dan kejelasan penyampaian, serta kemampuan siswa dalam menunjukkan langkah-langkah penyelesaian masalah.
- Soal essay tingkat kesulitan sulit menguji kemampuan siswa dalam mengaplikasikan konsep matematika yang kompleks dan memadukan beberapa konsep dalam menyelesaikan suatu masalah yang kompleks. Kriteria penilaian lebih fokus pada pemahaman konsep, keakuratan jawaban, dan kejelasan penyampaian, serta kemampuan siswa dalam menunjukkan langkah-langkah penyelesaian masalah, menganalisis data, dan menarik kesimpulan yang tepat.
Contoh Soal Essay Matematika dengan Tingkat Kesulitan yang Berbeda dan Rubrik Penilaian yang Sesuai
Berikut adalah tabel yang berisi contoh soal essay, tingkat kesulitan, dan rubrik penilaian yang digunakan:
| Contoh Soal Essay | Tingkat Kesulitan | Rubrik Penilaian |
|---|---|---|
| Jelaskan pengertian persamaan linear satu variabel dan berikan contohnya! | Mudah | Lihat Rubrik Penilaian |
| Hitunglah luas segitiga ABC dengan titik A (2, 3), B (5, 1), dan C (1, 0)! | Sedang | Lihat Rubrik Penilaian |
| Buktikan bahwa jumlah sudut-sudut dalam segitiga adalah 180 derajat! | Sulit | Lihat Rubrik Penilaian |
Keuntungan dan Kerugian Penggunaan Rubrik Penilaian Soal Essay Matematika
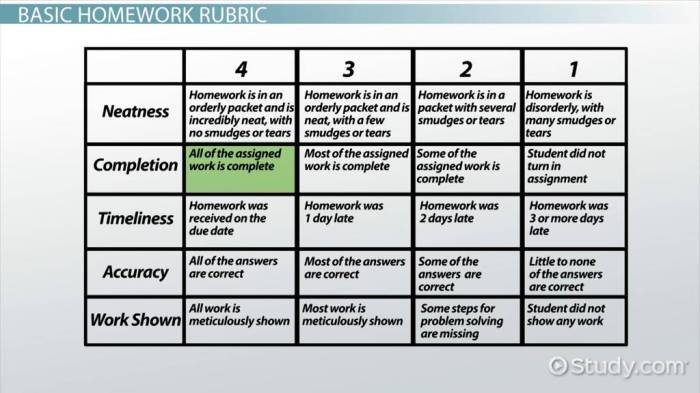
Rubrik penilaian merupakan alat yang efektif untuk menilai kemampuan siswa dalam menyelesaikan soal essay matematika. Rubrik ini memberikan panduan yang jelas dan terstruktur untuk menilai jawaban siswa berdasarkan kriteria yang telah ditentukan. Penggunaan rubrik ini memberikan beberapa keuntungan, namun juga memiliki beberapa kelemahan yang perlu dipertimbangkan.
Keuntungan Penggunaan Rubrik Penilaian Soal Essay Matematika
Penggunaan rubrik penilaian soal essay matematika memiliki beberapa keuntungan, antara lain:
- Meningkatkan Objektivitas Penilaian: Rubrik penilaian memberikan kriteria yang jelas dan terstruktur untuk menilai jawaban siswa. Hal ini membantu guru untuk menilai jawaban siswa secara objektif, tanpa dipengaruhi oleh bias atau faktor subjektif lainnya. Sebagai contoh, jika rubrik penilaian menentukan bahwa jawaban yang benar dan lengkap dengan penjelasan yang logis akan mendapatkan nilai maksimal, maka guru akan menilai jawaban siswa berdasarkan kriteria tersebut, bukan berdasarkan preferensi pribadi.
- Meningkatkan Konsistensi Penilaian: Rubrik penilaian membantu guru untuk menilai jawaban siswa secara konsisten, baik untuk satu kelas maupun untuk kelas yang berbeda. Hal ini karena rubrik penilaian memberikan panduan yang sama untuk menilai jawaban siswa. Sebagai contoh, jika rubrik penilaian digunakan untuk menilai jawaban siswa di kelas 10, maka guru dapat menggunakan rubrik yang sama untuk menilai jawaban siswa di kelas 11, sehingga penilaian menjadi lebih konsisten.
- Memudahkan Proses Penilaian: Rubrik penilaian membantu guru untuk menilai jawaban siswa dengan lebih mudah dan cepat. Hal ini karena rubrik penilaian memberikan panduan yang jelas dan terstruktur, sehingga guru tidak perlu menghabiskan waktu untuk merumuskan kriteria penilaian. Sebagai contoh, guru dapat langsung memberikan nilai berdasarkan kriteria yang telah ditentukan dalam rubrik penilaian, tanpa perlu menghabiskan waktu untuk membaca dan menganalisis jawaban siswa secara detail.
- Meningkatkan Transparansi Penilaian: Rubrik penilaian membantu siswa untuk memahami kriteria penilaian yang digunakan oleh guru. Hal ini membantu siswa untuk meningkatkan kualitas jawaban mereka dan memahami mengapa mereka mendapatkan nilai tertentu. Sebagai contoh, jika rubrik penilaian menunjukkan bahwa jawaban yang benar dan lengkap dengan penjelasan yang logis akan mendapatkan nilai maksimal, maka siswa akan berusaha untuk memberikan jawaban yang benar dan lengkap dengan penjelasan yang logis.
- Memudahkan Umpan Balik kepada Siswa: Rubrik penilaian membantu guru untuk memberikan umpan balik yang lebih spesifik dan terarah kepada siswa. Hal ini karena rubrik penilaian memberikan panduan yang jelas dan terstruktur untuk menilai jawaban siswa. Sebagai contoh, jika rubrik penilaian menunjukkan bahwa jawaban yang benar dan lengkap dengan penjelasan yang logis akan mendapatkan nilai maksimal, maka guru dapat memberikan umpan balik kepada siswa tentang bagaimana mereka dapat meningkatkan kualitas jawaban mereka dengan memberikan penjelasan yang lebih logis.
Kerugian Penggunaan Rubrik Penilaian Soal Essay Matematika, Contoh rubrik penilaian soal essay matematika
Penggunaan rubrik penilaian soal essay matematika juga memiliki beberapa kelemahan, antara lain:
- Sulit untuk Menilai Kreativitas dan Keaslian: Rubrik penilaian cenderung fokus pada kriteria yang terstruktur dan objektif, sehingga sulit untuk menilai kreativitas dan keaslian jawaban siswa. Sebagai contoh, jika rubrik penilaian hanya menilai jawaban yang benar dan lengkap, maka siswa yang memberikan jawaban yang kreatif dan orisinal mungkin tidak mendapatkan nilai yang tinggi, meskipun jawaban mereka menunjukkan pemahaman yang baik tentang materi.
- Tidak Fleksibel untuk Soal yang Kompleks: Rubrik penilaian mungkin tidak fleksibel untuk menilai soal yang kompleks dan membutuhkan penilaian yang lebih mendalam. Sebagai contoh, jika rubrik penilaian hanya menilai jawaban yang benar dan lengkap, maka sulit untuk menilai jawaban siswa yang menunjukkan pemahaman yang baik tentang materi, tetapi tidak memberikan jawaban yang benar dan lengkap.
- Membutuhkan Waktu dan Upaya untuk Dibuat: Membuat rubrik penilaian yang baik membutuhkan waktu dan upaya yang cukup. Hal ini karena guru harus merumuskan kriteria penilaian yang jelas, terstruktur, dan sesuai dengan tujuan pembelajaran. Sebagai contoh, guru harus merumuskan kriteria penilaian yang mengukur pemahaman siswa tentang konsep, kemampuan siswa dalam menyelesaikan masalah, dan kemampuan siswa dalam mengkomunikasikan jawaban mereka.
- Membutuhkan Penyesuaian untuk Setiap Soal: Rubrik penilaian harus disesuaikan dengan setiap soal yang diberikan. Hal ini karena setiap soal memiliki tingkat kesulitan dan kriteria penilaian yang berbeda. Sebagai contoh, rubrik penilaian untuk soal yang menanyakan tentang konsep dasar matematika akan berbeda dengan rubrik penilaian untuk soal yang menanyakan tentang aplikasi konsep matematika dalam kehidupan sehari-hari.
- Membutuhkan Kejelasan dan Konsistensi dalam Penerapannya: Penerapan rubrik penilaian harus dilakukan dengan jelas dan konsisten agar penilaian menjadi objektif dan adil. Sebagai contoh, jika rubrik penilaian menentukan bahwa jawaban yang benar dan lengkap dengan penjelasan yang logis akan mendapatkan nilai maksimal, maka guru harus menilai jawaban siswa berdasarkan kriteria tersebut, tanpa memberikan nilai yang lebih tinggi atau lebih rendah kepada siswa yang memiliki preferensi pribadi yang berbeda.
Ringkasan Penutup: Contoh Rubrik Penilaian Soal Essay Matematika
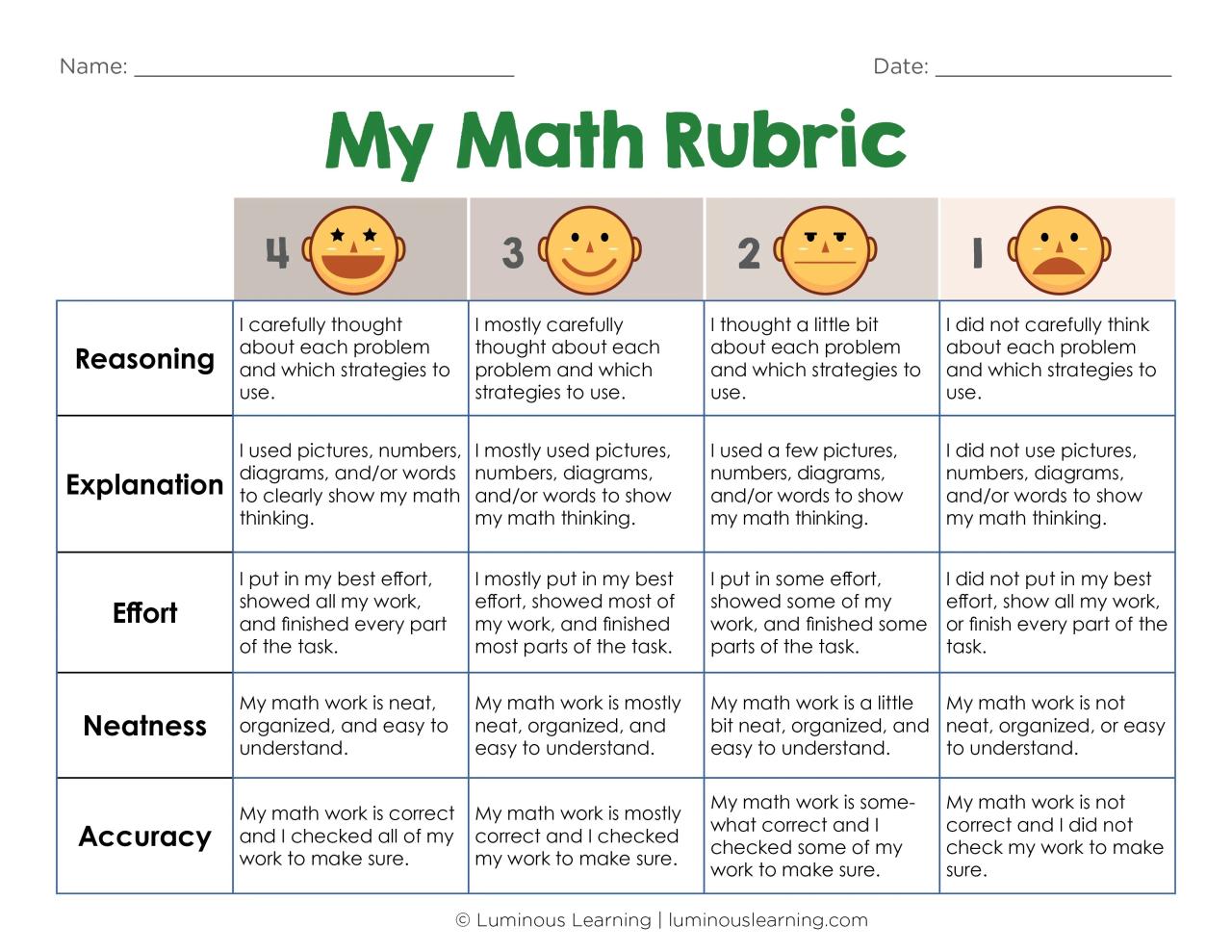
Dengan memahami konsep dan penerapan rubrik penilaian soal essay matematika, guru dapat meningkatkan kualitas penilaian dan memberikan umpan balik yang lebih efektif kepada siswa. Rubrik tidak hanya membantu dalam proses penilaian, tetapi juga membantu siswa memahami kriteria penilaian dan meningkatkan kemampuan mereka dalam menyelesaikan soal essay matematika.







