Contoh soal anova – Pernahkah Anda bertanya-tanya apakah ada perbedaan signifikan antara rata-rata nilai ujian siswa yang menggunakan metode pembelajaran A dan B? Atau mungkin ingin mengetahui pengaruh jenis pupuk terhadap hasil panen? Jika ya, maka Anda perlu mengenal teknik analisis data yang bernama ANOVA (Analysis of Variance). ANOVA adalah alat statistik yang kuat untuk membandingkan rata-rata dari dua atau lebih kelompok data, membantu Anda mengidentifikasi perbedaan signifikan yang mungkin tidak terlihat pada pandangan pertama.
Dalam artikel ini, kita akan menjelajahi dunia ANOVA melalui contoh soal yang menarik. Anda akan belajar bagaimana menerapkan ANOVA untuk menguji hipotesis, menginterpretasikan hasilnya, dan menarik kesimpulan yang bermakna. Mari kita mulai perjalanan kita untuk memahami kekuatan ANOVA dalam menganalisis data dan menemukan pola yang tersembunyi!
Pengertian ANOVA
ANOVA (Analysis of Variance) merupakan metode statistik yang digunakan untuk menguji perbedaan rata-rata populasi dengan membagi varians total data menjadi berbagai sumber varians. ANOVA merupakan alat yang ampuh untuk menganalisis data yang dikategorikan, seperti data yang dikumpulkan dari berbagai kelompok atau kondisi.
Konsep Dasar ANOVA
ANOVA didasarkan pada prinsip bahwa varians total data dapat dibagi menjadi beberapa komponen varians yang sesuai dengan faktor-faktor yang mempengaruhi data tersebut. Dengan membandingkan varians antara kelompok dengan varians dalam kelompok, ANOVA dapat menguji apakah terdapat perbedaan signifikan antara rata-rata kelompok.
Contoh Kasus Nyata
Sebagai contoh, bayangkan sebuah penelitian yang ingin membandingkan efektivitas tiga jenis pupuk pada pertumbuhan tanaman. Peneliti dapat menggunakan ANOVA untuk menguji apakah terdapat perbedaan signifikan dalam tinggi tanaman yang dihasilkan oleh masing-masing pupuk. Dalam kasus ini, faktor yang dipelajari adalah jenis pupuk, dan varians total tinggi tanaman dapat dibagi menjadi varians antara kelompok pupuk dan varians dalam kelompok pupuk.
Perbedaan ANOVA Satu Arah dan Dua Arah
ANOVA dapat diklasifikasikan menjadi dua jenis, yaitu ANOVA satu arah dan ANOVA dua arah. Perbedaan utama antara keduanya terletak pada jumlah faktor yang dipelajari.
| Karakteristik | ANOVA Satu Arah | ANOVA Dua Arah |
|---|---|---|
| Jumlah Faktor | Satu | Dua atau lebih |
| Tujuan | Menguji perbedaan rata-rata antara dua atau lebih kelompok berdasarkan satu faktor | Menguji perbedaan rata-rata antara dua atau lebih kelompok berdasarkan dua atau lebih faktor |
| Contoh | Menguji perbedaan tinggi tanaman berdasarkan jenis pupuk | Menguji perbedaan tinggi tanaman berdasarkan jenis pupuk dan jenis tanah |
Asumsi ANOVA
ANOVA, singkatan dari Analysis of Variance, adalah metode statistik yang digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok. ANOVA mengasumsikan bahwa data yang dianalisis memenuhi sejumlah asumsi tertentu. Pemenuhan asumsi ini sangat penting untuk memastikan bahwa hasil ANOVA akurat dan dapat diandalkan. Jika asumsi ANOVA tidak terpenuhi, hasil ANOVA mungkin tidak valid dan interpretasi hasil bisa menyesatkan.
Asumsi ANOVA
Asumsi ANOVA meliputi:
- Data berdistribusi normal: Asumsi ini menyatakan bahwa data dalam setiap kelompok harus mengikuti distribusi normal. Distribusi normal adalah distribusi probabilitas yang berbentuk seperti lonceng. Ini berarti bahwa sebagian besar data berada di sekitar rata-rata, dan semakin jauh dari rata-rata, semakin sedikit data yang ada.
- Varians sama: Asumsi ini menyatakan bahwa varians data dalam setiap kelompok harus sama. Varians adalah ukuran seberapa tersebar data. Jika varians tidak sama, maka uji ANOVA mungkin tidak akurat.
- Independensi data: Asumsi ini menyatakan bahwa data dalam setiap kelompok harus independen satu sama lain. Artinya, data dalam satu kelompok tidak boleh memengaruhi data dalam kelompok lain.
Memeriksa Asumsi ANOVA
Ada beberapa cara untuk memeriksa apakah asumsi ANOVA terpenuhi. Beberapa metode yang umum digunakan meliputi:
- Uji normalitas: Uji normalitas, seperti uji Shapiro-Wilk atau uji Kolmogorov-Smirnov, dapat digunakan untuk memeriksa apakah data dalam setiap kelompok mengikuti distribusi normal.
- Uji homogenitas varians: Uji homogenitas varians, seperti uji Levene atau uji Bartlett, dapat digunakan untuk memeriksa apakah varians data dalam setiap kelompok sama.
- Plot histogram dan boxplot: Plot histogram dan boxplot dapat membantu untuk memvisualisasikan distribusi data dan varians dalam setiap kelompok.
Contoh Data yang Melanggar Asumsi ANOVA, Contoh soal anova
Misalnya, bayangkan Anda ingin membandingkan efektivitas dua jenis pupuk pada pertumbuhan tanaman. Anda melakukan percobaan dengan menanam tanaman dalam dua kelompok, masing-masing diberi pupuk yang berbeda. Setelah beberapa minggu, Anda mengukur tinggi tanaman. Jika data tinggi tanaman tidak berdistribusi normal atau variansnya tidak sama, maka asumsi ANOVA tidak terpenuhi. Ini dapat menyebabkan hasil ANOVA yang tidak valid.
Konsekuensi Melanggar Asumsi ANOVA
Jika asumsi ANOVA tidak terpenuhi, maka hasil ANOVA mungkin tidak valid. Ini berarti bahwa kesimpulan yang ditarik dari hasil ANOVA mungkin tidak akurat. Konsekuensi melanggar asumsi ANOVA dapat meliputi:
- Peningkatan peluang kesalahan tipe I: Kesalahan tipe I terjadi ketika Anda menolak hipotesis nol yang sebenarnya benar. Jika asumsi ANOVA tidak terpenuhi, maka peluang kesalahan tipe I akan meningkat. Artinya, Anda lebih mungkin untuk menyimpulkan bahwa ada perbedaan signifikan antara kelompok-kelompok, padahal sebenarnya tidak ada.
- Penurunan daya uji: Daya uji adalah probabilitas untuk menolak hipotesis nol yang salah. Jika asumsi ANOVA tidak terpenuhi, maka daya uji akan menurun. Artinya, Anda kurang mungkin untuk menemukan perbedaan signifikan antara kelompok-kelompok, padahal sebenarnya ada.
- Hasil ANOVA yang menyesatkan: Jika asumsi ANOVA tidak terpenuhi, maka hasil ANOVA mungkin menyesatkan. Ini berarti bahwa kesimpulan yang ditarik dari hasil ANOVA mungkin tidak akurat dan dapat menyebabkan keputusan yang salah.
Jenis-Jenis ANOVA
Analisis varians (ANOVA) adalah alat statistik yang kuat untuk membandingkan rata-rata dari dua atau lebih kelompok. ANOVA memungkinkan kita untuk menguji apakah ada perbedaan signifikan antara rata-rata kelompok atau apakah perbedaan tersebut hanya terjadi karena variasi acak. Namun, ANOVA memiliki berbagai jenis yang perlu kita pahami agar dapat memilih metode yang tepat untuk menganalisis data kita.
Jenis-Jenis ANOVA Berdasarkan Jumlah Faktor dan Jumlah Kelompok
ANOVA dapat diklasifikasikan berdasarkan jumlah faktor yang dipertimbangkan dalam analisis dan jumlah kelompok dalam setiap faktor. Faktor adalah variabel independen yang ingin kita pelajari pengaruhnya terhadap variabel dependen. Berikut adalah beberapa jenis ANOVA:
- ANOVA Satu Faktor: ANOVA ini digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok yang didefinisikan oleh satu faktor. Contohnya, kita ingin mengetahui apakah ada perbedaan signifikan dalam skor ujian antara siswa yang menggunakan metode pembelajaran A, B, dan C. Dalam contoh ini, faktornya adalah metode pembelajaran (dengan tiga kelompok: A, B, dan C).
- ANOVA Dua Faktor: ANOVA ini digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok yang didefinisikan oleh dua faktor. Contohnya, kita ingin mengetahui apakah ada perbedaan signifikan dalam skor ujian antara siswa yang menggunakan metode pembelajaran A, B, dan C, dan juga dibagi berdasarkan jenis kelamin (laki-laki dan perempuan). Dalam contoh ini, faktornya adalah metode pembelajaran (dengan tiga kelompok: A, B, dan C) dan jenis kelamin (dengan dua kelompok: laki-laki dan perempuan).
- ANOVA Faktorial: ANOVA ini merupakan generalisasi dari ANOVA dua faktor, yang digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok yang didefinisikan oleh lebih dari dua faktor. Contohnya, kita ingin mengetahui apakah ada perbedaan signifikan dalam skor ujian antara siswa yang menggunakan metode pembelajaran A, B, dan C, dibagi berdasarkan jenis kelamin (laki-laki dan perempuan), dan juga dibagi berdasarkan tingkat kesulitan materi (mudah, sedang, sulit). Dalam contoh ini, faktornya adalah metode pembelajaran, jenis kelamin, dan tingkat kesulitan materi.
Contoh Soal untuk Setiap Jenis ANOVA
Berikut adalah contoh soal untuk setiap jenis ANOVA:
ANOVA Satu Faktor
Seorang peneliti ingin mengetahui apakah ada perbedaan signifikan dalam pertumbuhan tanaman yang diberi pupuk A, B, dan C. Ia menanam 10 tanaman untuk setiap jenis pupuk dan mengukur tinggi tanaman setelah 2 minggu. Data yang diperoleh disajikan dalam tabel berikut:
| Pupuk | Tinggi Tanaman (cm) |
|---|---|
| A | 10, 12, 11, 13, 14, 15, 16, 17, 18, 19 |
| B | 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 |
| C | 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 |
Peneliti dapat menggunakan ANOVA satu faktor untuk menguji apakah ada perbedaan signifikan dalam tinggi tanaman antara kelompok yang diberi pupuk A, B, dan C.
ANOVA Dua Faktor
Seorang guru ingin mengetahui apakah ada perbedaan signifikan dalam skor ujian siswa yang menggunakan metode pembelajaran A dan B, dan juga dibagi berdasarkan jenis kelamin (laki-laki dan perempuan). Ia memberikan metode pembelajaran A kepada 20 siswa laki-laki dan 20 siswa perempuan, dan metode pembelajaran B kepada 20 siswa laki-laki dan 20 siswa perempuan. Data yang diperoleh disajikan dalam tabel berikut:
| Metode Pembelajaran | Jenis Kelamin | Skor Ujian |
|---|---|---|
| A | Laki-laki | 70, 75, 80, 85, 90, 72, 77, 82, 87, 92, … |
| A | Perempuan | 65, 70, 75, 80, 85, 67, 72, 77, 82, 87, … |
| B | Laki-laki | 60, 65, 70, 75, 80, 62, 67, 72, 77, 82, … |
| B | Perempuan | 55, 60, 65, 70, 75, 57, 62, 67, 72, 77, … |
Guru dapat menggunakan ANOVA dua faktor untuk menguji apakah ada perbedaan signifikan dalam skor ujian antara kelompok yang menggunakan metode pembelajaran A dan B, dan juga dibagi berdasarkan jenis kelamin.
Perbedaan Antara ANOVA Satu Faktor dan ANOVA Dua Faktor
Berikut adalah tabel yang menunjukkan perbedaan antara ANOVA satu faktor dan ANOVA dua faktor:
| Fitur | ANOVA Satu Faktor | ANOVA Dua Faktor |
|---|---|---|
| Jumlah Faktor | Satu | Dua |
| Jumlah Kelompok | Dua atau lebih | Dua atau lebih untuk setiap faktor |
| Tujuan Analisis | Membandingkan rata-rata dari dua atau lebih kelompok yang didefinisikan oleh satu faktor | Membandingkan rata-rata dari dua atau lebih kelompok yang didefinisikan oleh dua faktor |
| Contoh Soal | Membandingkan tinggi tanaman yang diberi pupuk A, B, dan C | Membandingkan skor ujian siswa yang menggunakan metode pembelajaran A dan B, dan juga dibagi berdasarkan jenis kelamin |
Langkah-Langkah Melakukan ANOVA
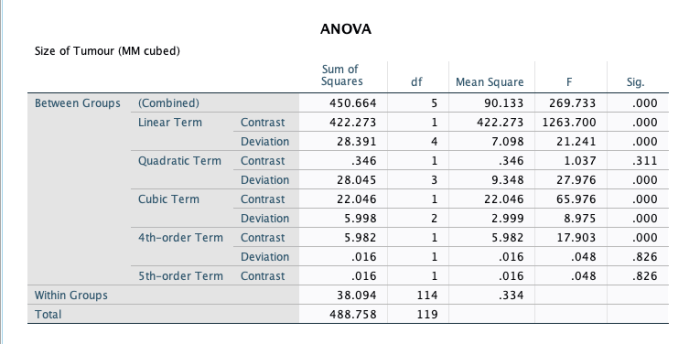
Analisis Varian (ANOVA) adalah metode statistik yang digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok. ANOVA memungkinkan kita untuk menentukan apakah terdapat perbedaan yang signifikan antara rata-rata kelompok, atau apakah perbedaan tersebut terjadi secara kebetulan. Metode ini sangat berguna dalam berbagai bidang, seperti penelitian medis, ilmu sosial, dan bisnis.
Langkah-Langkah ANOVA
Berikut adalah langkah-langkah yang diperlukan untuk melakukan analisis ANOVA:
- Rumuskan Hipotesis: Langkah pertama adalah merumuskan hipotesis nol dan hipotesis alternatif. Hipotesis nol menyatakan bahwa tidak ada perbedaan yang signifikan antara rata-rata kelompok, sedangkan hipotesis alternatif menyatakan bahwa terdapat perbedaan yang signifikan.
- Pilih Tingkat Alfa: Tingkat alfa adalah probabilitas menolak hipotesis nol ketika sebenarnya benar. Tingkat alfa biasanya ditetapkan pada 0,05, yang berarti bahwa terdapat 5% kemungkinan menolak hipotesis nol ketika sebenarnya benar.
- Kumpulkan Data: Langkah selanjutnya adalah mengumpulkan data dari setiap kelompok yang ingin dibandingkan. Data haruslah independen dan terdistribusi normal.
- Hitung Statistik Uji: Statistik uji untuk ANOVA adalah F-statistik. F-statistik adalah rasio varians antar kelompok dengan varians dalam kelompok. Statistik uji ini dihitung dengan membagi varians antar kelompok dengan varians dalam kelompok.
- Tentukan Nilai P: Nilai P adalah probabilitas mendapatkan statistik uji yang sama atau lebih ekstrem daripada yang diamati, dengan asumsi hipotesis nol benar. Nilai P dihitung menggunakan tabel distribusi F atau dengan menggunakan perangkat lunak statistik.
- Buat Keputusan: Jika nilai P lebih kecil dari tingkat alfa, maka hipotesis nol ditolak. Ini berarti bahwa terdapat perbedaan yang signifikan antara rata-rata kelompok. Jika nilai P lebih besar dari tingkat alfa, maka hipotesis nol tidak ditolak. Ini berarti bahwa tidak ada perbedaan yang signifikan antara rata-rata kelompok.
Contoh Soal
Misalnya, kita ingin membandingkan efektivitas tiga jenis obat baru untuk mengobati depresi. Kita dapat menggunakan ANOVA untuk menentukan apakah terdapat perbedaan yang signifikan antara efektivitas ketiga obat tersebut. Hipotesis nol adalah bahwa tidak ada perbedaan yang signifikan antara efektivitas ketiga obat tersebut, sedangkan hipotesis alternatif adalah bahwa terdapat perbedaan yang signifikan.
Kita dapat mengumpulkan data dari tiga kelompok pasien, masing-masing menerima salah satu dari tiga obat. Data yang dikumpulkan dapat berupa skor depresi sebelum dan sesudah pengobatan. Kita kemudian dapat menghitung statistik uji F dan nilai P untuk menentukan apakah terdapat perbedaan yang signifikan antara efektivitas ketiga obat tersebut.
Flowchart ANOVA
Berikut adalah flowchart yang menggambarkan proses analisis ANOVA:
[Gambar flowchart ANOVA]
Flowchart ini menunjukkan langkah-langkah yang terlibat dalam analisis ANOVA, mulai dari perumusan hipotesis hingga pembuatan keputusan.
Interpretasi Hasil ANOVA
Setelah melakukan analisis ANOVA, langkah selanjutnya adalah menginterpretasikan hasil yang diperoleh. Interpretasi ini membantu kita dalam menarik kesimpulan mengenai perbedaan rata-rata populasi yang diuji.
Memahami Tabel ANOVA
Hasil analisis ANOVA biasanya disajikan dalam tabel yang menunjukkan nilai-nilai penting seperti nilai F, nilai p, dan derajat kebebasan. Untuk memahami tabel ANOVA, kita perlu memahami makna dari setiap nilai tersebut.
| Nilai | Makna |
|---|---|
| F | Nilai F adalah statistik uji yang mengukur variabilitas antar kelompok terhadap variabilitas dalam kelompok. Semakin besar nilai F, semakin kuat bukti bahwa terdapat perbedaan signifikan antar kelompok. |
| p | Nilai p adalah probabilitas mendapatkan hasil yang diamati atau lebih ekstrem jika tidak ada perbedaan nyata antar kelompok. Nilai p yang kecil (biasanya kurang dari 0,05) menunjukkan bukti yang kuat untuk menolak hipotesis nol bahwa tidak ada perbedaan antar kelompok. |
| Derajat Kebebasan | Derajat kebebasan menunjukkan jumlah informasi bebas yang tersedia dalam data. Dalam ANOVA, derajat kebebasan untuk faktor (antara kelompok) adalah jumlah kelompok dikurangi 1, sedangkan derajat kebebasan untuk error (dalam kelompok) adalah jumlah total observasi dikurangi jumlah kelompok. |
Contoh Interpretasi Hasil ANOVA
Misalnya, kita ingin menguji apakah terdapat perbedaan signifikan dalam nilai ujian mahasiswa di tiga metode pembelajaran yang berbeda. Hasil analisis ANOVA menunjukkan nilai F sebesar 5.23 dan nilai p sebesar 0.01. Dengan nilai p kurang dari 0.05, kita menolak hipotesis nol dan menyimpulkan bahwa terdapat perbedaan signifikan dalam nilai ujian mahasiswa di antara ketiga metode pembelajaran tersebut.
Namun, analisis ANOVA tidak menunjukkan metode pembelajaran mana yang lebih efektif. Untuk mengetahui hal ini, kita perlu melakukan uji lanjutan seperti uji Tukey HSD atau uji Scheffé. Uji lanjutan ini membantu kita dalam menentukan kelompok mana yang memiliki rata-rata yang berbeda secara signifikan.
Contoh Soal ANOVA
ANOVA (Analysis of Variance) adalah teknik statistik yang digunakan untuk menguji perbedaan rata-rata dari dua atau lebih kelompok data. Teknik ini sangat berguna dalam berbagai bidang, seperti penelitian medis, ilmu sosial, dan bisnis.
Contoh Soal ANOVA dengan 3 Kelompok Data
Misalkan kita ingin mengetahui apakah ada perbedaan signifikan dalam nilai ujian matematika antara tiga kelas yang berbeda.
- Kelas A: 70, 75, 80, 85, 90
- Kelas B: 65, 70, 75, 80, 85
- Kelas C: 80, 85, 90, 95, 100
Menentukan Hipotesis Nol dan Hipotesis Alternatif
Sebelum melakukan analisis ANOVA, kita perlu menentukan hipotesis nol dan hipotesis alternatif.
- Hipotesis Nol (H0): Tidak ada perbedaan signifikan dalam rata-rata nilai ujian matematika antara tiga kelas.
- Hipotesis Alternatif (H1): Ada perbedaan signifikan dalam rata-rata nilai ujian matematika antara tiga kelas.
Langkah-langkah Analisis ANOVA
Berikut adalah langkah-langkah analisis ANOVA untuk contoh soal di atas:
- Hitung rata-rata nilai ujian matematika untuk setiap kelas:
- Rata-rata kelas A = (70 + 75 + 80 + 85 + 90) / 5 = 80
- Rata-rata kelas B = (65 + 70 + 75 + 80 + 85) / 5 = 75
- Rata-rata kelas C = (80 + 85 + 90 + 95 + 100) / 5 = 90
- Hitung varians untuk setiap kelas:
- Varians kelas A = [(70-80)^2 + (75-80)^2 + (80-80)^2 + (85-80)^2 + (90-80)^2] / (5-1) = 50
- Varians kelas B = [(65-75)^2 + (70-75)^2 + (75-75)^2 + (80-75)^2 + (85-75)^2] / (5-1) = 50
- Varians kelas C = [(80-90)^2 + (85-90)^2 + (90-90)^2 + (95-90)^2 + (100-90)^2] / (5-1) = 50
- Hitung varians antar kelompok (between-group variance):
- Varians antar kelompok = [(80-85)^2 + (75-85)^2 + (90-85)^2] / (3-1) = 125
- Hitung varians dalam kelompok (within-group variance):
- Varians dalam kelompok = (50 + 50 + 50) / 3 = 50
- Hitung statistik F:
- Statistik F = Varians antar kelompok / Varians dalam kelompok = 125 / 50 = 2.5
- Cari nilai p:
- Nilai p adalah probabilitas mendapatkan hasil seperti yang kita amati atau lebih ekstrem jika hipotesis nol benar. Untuk mencari nilai p, kita perlu menggunakan tabel distribusi F atau software statistik.
- Ambil keputusan:
- Jika nilai p lebih kecil dari tingkat signifikansi (biasanya 0.05), kita menolak hipotesis nol. Artinya, ada perbedaan signifikan dalam rata-rata nilai ujian matematika antara tiga kelas.
- Jika nilai p lebih besar dari tingkat signifikansi, kita gagal menolak hipotesis nol. Artinya, tidak ada perbedaan signifikan dalam rata-rata nilai ujian matematika antara tiga kelas.
Aplikasi ANOVA dalam Penelitian
Analisis Varian (ANOVA) merupakan alat statistik yang kuat dan serbaguna dalam penelitian, khususnya dalam analisis data yang melibatkan perbandingan rata-rata kelompok. ANOVA memungkinkan peneliti untuk menguji perbedaan signifikan antara kelompok-kelompok, sehingga dapat membantu dalam pengambilan keputusan yang lebih terinformasi.
Contoh Aplikasi ANOVA dalam Penelitian
ANOVA memiliki berbagai aplikasi dalam berbagai disiplin ilmu, seperti:
- Ilmu Kesehatan: Membandingkan efektivitas dua jenis pengobatan untuk penyakit tertentu.
- Psikologi: Menganalisis perbedaan dalam tingkat stres antara kelompok pekerja yang mengalami tingkat tekanan kerja yang berbeda.
- Pendidikan: Membandingkan kinerja siswa yang mengikuti dua metode pembelajaran yang berbeda.
- Bisnis: Menganalisis efektivitas dua strategi pemasaran yang berbeda pada penjualan produk.
- Pertanian: Membandingkan hasil panen dari berbagai jenis pupuk.
Keunggulan ANOVA dalam Penelitian
ANOVA memiliki beberapa keunggulan yang menjadikannya alat statistik yang populer dalam penelitian:
- Memungkinkan perbandingan beberapa kelompok secara bersamaan: ANOVA dapat menguji perbedaan antara dua atau lebih kelompok secara bersamaan, sehingga lebih efisien daripada melakukan uji t berulang kali.
- Memperhatikan variabilitas dalam data: ANOVA mempertimbangkan variabilitas dalam data dan mengukur seberapa besar variabilitas ini disebabkan oleh perbedaan antara kelompok atau oleh variabilitas dalam kelompok itu sendiri.
- Relatif mudah dipahami dan diterapkan: Meskipun konsep dasarnya agak kompleks, ANOVA relatif mudah dipahami dan diterapkan dengan bantuan perangkat lunak statistik.
- Menghasilkan hasil yang lebih akurat: ANOVA dapat menghasilkan hasil yang lebih akurat dibandingkan dengan uji t berulang kali, terutama ketika jumlah kelompok yang dibandingkan banyak.
Keterbatasan ANOVA dalam Penelitian
Meskipun memiliki banyak keunggulan, ANOVA juga memiliki beberapa keterbatasan yang perlu diperhatikan:
- Data harus normal: ANOVA mengasumsikan bahwa data terdistribusi normal. Jika data tidak normal, maka hasil ANOVA mungkin tidak akurat.
- Varians kelompok harus sama: ANOVA mengasumsikan bahwa varians kelompok yang dibandingkan sama. Jika varians kelompok tidak sama, maka hasil ANOVA mungkin tidak akurat.
- Tidak dapat menganalisis data non-numerik: ANOVA hanya dapat menganalisis data numerik. Jika data tidak numerik, maka perlu digunakan metode statistik lain.
- Membutuhkan ukuran sampel yang cukup besar: ANOVA membutuhkan ukuran sampel yang cukup besar untuk menghasilkan hasil yang akurat. Jika ukuran sampel terlalu kecil, maka hasil ANOVA mungkin tidak akurat.
Ilustrasi Penggunaan ANOVA dalam Pengambilan Keputusan
Misalnya, seorang peneliti ingin menguji efektivitas tiga jenis metode pembelajaran (A, B, dan C) pada kinerja siswa dalam ujian matematika. Peneliti mengumpulkan data tentang nilai ujian matematika dari 60 siswa yang dibagi secara acak ke dalam tiga kelompok (20 siswa per kelompok), dengan masing-masing kelompok mengikuti metode pembelajaran yang berbeda.
Dengan menggunakan ANOVA, peneliti dapat menguji apakah ada perbedaan signifikan dalam nilai ujian matematika antara tiga kelompok siswa. Jika hasil ANOVA menunjukkan perbedaan signifikan, maka peneliti dapat menyimpulkan bahwa metode pembelajaran yang berbeda memiliki efek yang berbeda pada kinerja siswa. Berdasarkan hasil ini, peneliti dapat merekomendasikan metode pembelajaran yang paling efektif untuk meningkatkan kinerja siswa dalam ujian matematika.
Perangkat Lunak untuk Analisis ANOVA
Analisis ANOVA (Analysis of Variance) merupakan teknik statistik yang kuat untuk membandingkan rata-rata dari dua atau lebih kelompok data. Untuk memudahkan proses analisis, berbagai perangkat lunak statistik telah dikembangkan, menawarkan fitur-fitur yang membantu dalam menjalankan dan menginterpretasikan hasil ANOVA.
Perangkat Lunak Populer
Berikut adalah beberapa perangkat lunak populer yang dapat digunakan untuk analisis ANOVA:
- SPSS (Statistical Package for the Social Sciences): Perangkat lunak statistik yang sangat populer dan serbaguna, SPSS menawarkan berbagai fitur untuk analisis ANOVA, termasuk desain satu faktor, dua faktor, dan ANOVA berulang. SPSS menyediakan antarmuka pengguna yang ramah dan dilengkapi dengan panduan yang mudah dipahami, membuatnya ideal untuk pengguna pemula dan ahli.
- R: Bahasa pemrograman statistik yang gratis dan open-source, R menawarkan fleksibilitas yang tinggi dalam analisis ANOVA. R menyediakan berbagai paket statistik, termasuk paket “stats” yang menyediakan fungsi untuk analisis ANOVA. R sangat cocok untuk peneliti yang membutuhkan kontrol penuh atas proses analisis dan ingin melakukan penyesuaian.
- Microsoft Excel: Perangkat lunak spreadsheet yang umum digunakan, Excel juga memiliki fitur untuk analisis ANOVA. Meskipun fitur ANOVA Excel tidak selengkap SPSS atau R, Excel dapat digunakan untuk analisis ANOVA sederhana dengan bantuan alat Analysis ToolPak.
- JMP (Statistical Discovery): Perangkat lunak statistik yang fokus pada visualisasi data dan eksplorasi, JMP menawarkan fitur yang kuat untuk analisis ANOVA. JMP menyediakan antarmuka pengguna yang intuitif dan visual, membuatnya mudah untuk menjelajahi data dan mengidentifikasi pola.
- Minitab: Perangkat lunak statistik yang dirancang untuk analisis statistik dan peningkatan kualitas, Minitab menyediakan fitur yang komprehensif untuk analisis ANOVA. Minitab menawarkan antarmuka yang mudah digunakan dan dilengkapi dengan panduan yang jelas, membuatnya cocok untuk pengguna dengan berbagai tingkat keahlian.
Fitur Utama Perangkat Lunak ANOVA
Fitur-fitur utama yang umumnya ditemukan dalam perangkat lunak ANOVA meliputi:
- Desain ANOVA: Perangkat lunak ANOVA memungkinkan Anda untuk menentukan desain ANOVA yang sesuai dengan data Anda, seperti desain satu faktor, dua faktor, atau ANOVA berulang.
- Pengujian Hipotesis: Perangkat lunak ANOVA membantu Anda dalam menguji hipotesis statistik yang terkait dengan perbedaan rata-rata kelompok.
- Tabel ANOVA: Perangkat lunak ANOVA menampilkan tabel ANOVA yang merangkum hasil analisis, termasuk statistik F, nilai p, dan derajat kebebasan.
- Visualisasi Data: Perangkat lunak ANOVA memungkinkan Anda untuk memvisualisasikan data Anda dengan grafik yang membantu dalam menginterpretasikan hasil.
- Laporan: Perangkat lunak ANOVA dapat menghasilkan laporan yang lengkap dan mudah dibaca yang merangkum hasil analisis.
Contoh Penggunaan Perangkat Lunak ANOVA
Misalnya, Anda ingin membandingkan efektivitas tiga jenis pupuk pada pertumbuhan tanaman. Anda dapat menggunakan perangkat lunak ANOVA untuk menguji apakah ada perbedaan signifikan dalam tinggi tanaman yang dirawat dengan tiga jenis pupuk tersebut. Anda dapat memasukkan data tinggi tanaman ke dalam perangkat lunak ANOVA, menentukan desain ANOVA yang sesuai, dan menjalankan analisis. Perangkat lunak ANOVA akan menampilkan tabel ANOVA yang merangkum hasil analisis, termasuk statistik F, nilai p, dan derajat kebebasan. Berdasarkan hasil analisis, Anda dapat menyimpulkan apakah ada perbedaan signifikan dalam tinggi tanaman yang dirawat dengan tiga jenis pupuk tersebut.
Contoh soal ANOVA seringkali muncul dalam mata kuliah statistika, membahas tentang perbandingan rata-rata dari beberapa kelompok data. Nah, dalam analisis data keuangan, seringkali kita juga menemukan perbandingan, seperti pada contoh soal rekonsiliasi fiskal contoh soal rekonsiliasi fiskal. Di sini, kita membandingkan data keuangan perusahaan dengan data pajak yang dilaporkan, untuk melihat kesesuaiannya.
Konsep perbandingan ini juga dapat diterapkan dalam soal ANOVA, membantu kita dalam menganalisis dan memahami data yang kompleks.
Pentingnya Memahaman ANOVA: Contoh Soal Anova
ANOVA, singkatan dari Analysis of Variance, adalah metode statistik yang kuat dan serbaguna yang digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok. Pemahaman tentang ANOVA sangat penting dalam berbagai bidang, termasuk ilmu sosial, kedokteran, bisnis, dan teknik. Dalam dunia yang didorong oleh data, kemampuan untuk menganalisis dan menginterpretasikan data dengan tepat menjadi semakin penting. ANOVA memberikan alat yang ampuh untuk mengungkap pola dan hubungan yang tersembunyi dalam data, memungkinkan kita untuk membuat kesimpulan yang bermakna dan mengambil keputusan yang lebih baik.
Manfaat Mempelajari ANOVA
Mempelajari ANOVA memiliki banyak manfaat, baik untuk individu maupun organisasi. Beberapa manfaat utama meliputi:
- Pengambilan Keputusan yang Lebih Baik: ANOVA membantu dalam mengidentifikasi perbedaan yang signifikan antara kelompok, yang memungkinkan kita untuk membuat keputusan yang lebih tepat dan efektif. Misalnya, dalam pemasaran, ANOVA dapat digunakan untuk membandingkan efektivitas kampanye iklan yang berbeda, sehingga perusahaan dapat mengalokasikan sumber daya mereka dengan lebih efisien.
- Pemahaman yang Lebih Dalam tentang Data: ANOVA memungkinkan kita untuk mengungkap pola dan hubungan yang tersembunyi dalam data, yang mengarah pada pemahaman yang lebih dalam tentang fenomena yang sedang dipelajari. Misalnya, dalam penelitian medis, ANOVA dapat digunakan untuk mengidentifikasi faktor-faktor yang mempengaruhi efektivitas pengobatan baru, yang mengarah pada pengembangan strategi pengobatan yang lebih efektif.
- Meningkatkan Keakuratan Penelitian: ANOVA membantu dalam mengurangi kesalahan dan meningkatkan keakuratan penelitian dengan mengendalikan variabilitas dalam data. Ini sangat penting dalam penelitian ilmiah, di mana hasil yang akurat dan dapat diandalkan sangat penting untuk kemajuan ilmu pengetahuan.
- Meningkatkan Kemampuan Analisis Data: Mempelajari ANOVA meningkatkan kemampuan analisis data Anda, yang memungkinkan Anda untuk menginterpretasikan data dengan lebih baik dan mengidentifikasi pola yang mungkin tidak terlihat pada pandangan pertama. Keterampilan ini sangat berharga dalam berbagai bidang, baik di akademisi maupun di dunia profesional.
Contoh Pemahaman ANOVA dalam Memecahkan Masalah
Bayangkan Anda adalah seorang manajer produksi di sebuah perusahaan manufaktur. Anda ingin mengetahui apakah ada perbedaan yang signifikan dalam kualitas produk yang dihasilkan oleh tiga mesin produksi yang berbeda. Anda dapat menggunakan ANOVA untuk menguji hipotesis ini. Dengan menjalankan analisis ANOVA, Anda dapat menentukan apakah ada perbedaan yang signifikan dalam kualitas produk yang dihasilkan oleh ketiga mesin tersebut. Jika ada perbedaan yang signifikan, Anda dapat menyelidiki lebih lanjut untuk mengidentifikasi sumber perbedaan dan mengambil langkah-langkah untuk meningkatkan kualitas produk.
Contoh lain adalah dalam penelitian medis. Peneliti ingin mengetahui apakah ada perbedaan yang signifikan dalam efektivitas dua jenis pengobatan untuk suatu penyakit. Mereka dapat menggunakan ANOVA untuk menguji hipotesis ini. Dengan menganalisis data dari uji klinis, mereka dapat menentukan apakah ada perbedaan yang signifikan dalam efektivitas kedua pengobatan tersebut. Jika ada perbedaan yang signifikan, mereka dapat merekomendasikan pengobatan yang lebih efektif untuk pasien.
Ringkasan Akhir
Dengan memahami konsep ANOVA, Anda memiliki alat yang ampuh untuk menganalisis data dan menguji hipotesis. Dari penelitian ilmiah hingga analisis bisnis, ANOVA membantu Anda memahami perbedaan signifikan antar kelompok data, sehingga dapat membantu Anda dalam pengambilan keputusan yang lebih tepat dan efektif.




