Contoh soal berpangkat – Pernahkah kamu bertanya-tanya bagaimana cara menghitung luas persegi dengan cepat? Atau bagaimana cara menuliskan angka yang sangat besar dengan lebih ringkas? Nah, konsep pangkat dalam matematika bisa menjadi jawabannya. Pangkat adalah operasi matematika yang melibatkan perkalian berulang suatu bilangan dengan dirinya sendiri. Dengan memahami konsep ini, kamu akan dapat menyelesaikan berbagai soal matematika yang melibatkan bilangan besar, pecahan, desimal, akar, variabel, dan bahkan kombinasi operasi.
Dalam artikel ini, kita akan menjelajahi dunia pangkat dengan contoh soal yang menarik dan mudah dipahami. Mulai dari soal sederhana hingga soal yang lebih kompleks, kita akan mengupas tuntas konsep pangkat dan cara mengaplikasikannya dalam berbagai situasi. Siap-siap untuk mengasah kemampuanmu dan melangkah lebih jauh dalam memahami matematika!
Pengertian Pangkat
Pangkat dalam matematika adalah operasi yang mengulang perkalian suatu bilangan dengan dirinya sendiri beberapa kali. Operasi ini ditandai dengan tanda pangkat (^) atau superskrip. Pangkat terdiri dari dua bagian, yaitu basis dan eksponen. Basis adalah bilangan yang dikalikan dengan dirinya sendiri, sedangkan eksponen menunjukkan berapa kali basis dikalikan.
Contoh Penggunaan Pangkat dalam Kehidupan Sehari-hari
Pangkat sering digunakan dalam berbagai aspek kehidupan sehari-hari. Misalnya, saat menghitung luas persegi, kita menggunakan pangkat dua. Jika sisi persegi adalah 5 cm, maka luasnya adalah 52 cm2 = 25 cm2. Contoh lainnya, dalam ilmu komputer, satuan data seperti kilobyte (KB), megabyte (MB), gigabyte (GB) menggunakan pangkat dua untuk menunjukkan ukuran data. 1 KB = 210 byte, 1 MB = 220 byte, dan 1 GB = 230 byte.
Perbedaan Pangkat Positif dan Pangkat Negatif
| Pangkat | Definisi | Contoh |
|---|---|---|
| Pangkat Positif | Bilangan dikalikan dengan dirinya sendiri sebanyak eksponen kali. | 23 = 2 x 2 x 2 = 8 |
| Pangkat Negatif | Bilangan dibalik (dijadikan pecahan) dan dikalikan dengan dirinya sendiri sebanyak eksponen kali. | 2-3 = 1 / 23 = 1 / (2 x 2 x 2) = 1/8 |
Sifat-sifat Pangkat
Setelah memahami definisi pangkat, kita akan menjelajahi sifat-sifatnya. Sifat-sifat ini akan memudahkan kita dalam menyelesaikan operasi pangkat, terutama dalam persamaan dan soal-soal matematika.
Perkalian Pangkat dengan Basis Sama
Sifat pertama yang akan kita bahas adalah perkalian pangkat dengan basis yang sama. Sifat ini menyatakan bahwa jika kita mengalikan dua pangkat dengan basis yang sama, maka hasilnya adalah pangkat dengan basis yang sama dan eksponen yang merupakan jumlah dari kedua eksponen tersebut.
am × an = am+n
Sebagai contoh, perhatikan operasi 23 × 22. Berdasarkan sifat perkalian pangkat dengan basis sama, kita dapat menyelesaikannya sebagai berikut:
- 23 × 22 = 23+2
- = 25
- = 32
Pembagian Pangkat dengan Basis Sama
Sifat kedua yang perlu kita ketahui adalah pembagian pangkat dengan basis yang sama. Sifat ini menyatakan bahwa jika kita membagi dua pangkat dengan basis yang sama, maka hasilnya adalah pangkat dengan basis yang sama dan eksponen yang merupakan selisih dari kedua eksponen tersebut.
am ÷ an = am-n
Misalnya, perhatikan operasi 35 ÷ 32. Kita dapat menyelesaikannya dengan menggunakan sifat pembagian pangkat dengan basis sama:
- 35 ÷ 32 = 35-2
- = 33
- = 27
Perpangkatan Pangkat
Sifat ketiga adalah perpangkatan pangkat. Sifat ini menyatakan bahwa jika kita memangkatkan sebuah pangkat dengan eksponen lain, maka hasilnya adalah pangkat dengan basis yang sama dan eksponen yang merupakan hasil kali dari kedua eksponen tersebut.
(am)n = am×n
Contohnya, perhatikan operasi (42)3. Kita dapat menyelesaikannya dengan menggunakan sifat perpangkatan pangkat:
- (42)3 = 42×3
- = 46
- = 4096
Pangkat Nol
Sifat keempat adalah pangkat nol. Sifat ini menyatakan bahwa setiap bilangan yang dipangkatkan dengan nol akan menghasilkan 1.
a0 = 1
Sebagai contoh, 50 = 1.
Pangkat Negatif
Sifat kelima adalah pangkat negatif. Sifat ini menyatakan bahwa pangkat negatif sama dengan kebalikan dari pangkat positif dengan eksponen yang sama.
a-n = 1/an
Contohnya, 2-3 = 1/23 = 1/8.
Tabel Sifat Pangkat
| Sifat | Rumus | Contoh |
|---|---|---|
| Perkalian Pangkat dengan Basis Sama | am × an = am+n | 23 × 22 = 23+2 = 25 = 32 |
| Pembagian Pangkat dengan Basis Sama | am ÷ an = am-n | 35 ÷ 32 = 35-2 = 33 = 27 |
| Perpangkatan Pangkat | (am)n = am×n | (42)3 = 42×3 = 46 = 4096 |
| Pangkat Nol | a0 = 1 | 50 = 1 |
| Pangkat Negatif | a-n = 1/an | 2-3 = 1/23 = 1/8 |
Soal Pangkat Sederhana
Soal pangkat sederhana merupakan soal yang melibatkan operasi perpangkatan dengan bilangan bulat positif. Operasi perpangkatan adalah perkalian berulang dari suatu bilangan dengan dirinya sendiri. Pangkat menunjukkan berapa kali bilangan tersebut dikalikan dengan dirinya sendiri.
Contoh Soal Pangkat Sederhana dengan Bilangan Bulat Positif
Berikut adalah 5 contoh soal pangkat sederhana yang melibatkan bilangan bulat positif beserta langkah-langkah penyelesaiannya:
-
Soal: Hitunglah nilai dari 23.
Penyelesaian: 23 = 2 x 2 x 2 = 8
-
Soal: Berapakah hasil dari 34?
Penyelesaian: 34 = 3 x 3 x 3 x 3 = 81
-
Soal: Tentukan nilai dari 52.
Penyelesaian: 52 = 5 x 5 = 25
-
Soal: Hitunglah nilai dari 43.
Penyelesaian: 43 = 4 x 4 x 4 = 64
-
Soal: Berapakah hasil dari 102?
Penyelesaian: 102 = 10 x 10 = 100
Contoh Soal Pangkat Sederhana dengan Bilangan Bulat Negatif
Soal pangkat yang melibatkan bilangan bulat negatif memiliki aturan khusus. Jika pangkatnya genap, hasilnya positif. Jika pangkatnya ganjil, hasilnya negatif.
Contohnya:
-
Soal: Hitunglah nilai dari (-2)4.
Penyelesaian: (-2)4 = (-2) x (-2) x (-2) x (-2) = 16
-
Soal: Berapakah hasil dari (-3)3?
Penyelesaian: (-3)3 = (-3) x (-3) x (-3) = -27
Soal Pangkat Pecahan
Soal pangkat yang melibatkan bilangan pecahan merupakan bentuk yang lebih kompleks dari soal pangkat biasa. Dalam soal ini, kita perlu memahami bagaimana cara mengalikan bilangan pecahan dengan dirinya sendiri beberapa kali, sesuai dengan nilai pangkatnya.
Contoh Soal Pangkat Pecahan
Berikut ini tiga contoh soal pangkat yang melibatkan bilangan pecahan, beserta langkah-langkah penyelesaiannya:
-
Hitunglah nilai dari (1/2)3.
Penyelesaian:
- Pangkat 3 menunjukkan bahwa kita perlu mengalikan (1/2) dengan dirinya sendiri sebanyak tiga kali.
- Maka, (1/2)3 = (1/2) x (1/2) x (1/2) = 1/8.
-
Tentukan nilai dari (2/3)2.
Penyelesaian:
- Pangkat 2 menunjukkan bahwa kita perlu mengalikan (2/3) dengan dirinya sendiri sebanyak dua kali.
- Maka, (2/3)2 = (2/3) x (2/3) = 4/9.
-
Hitunglah nilai dari (3/4)-2.
Penyelesaian:
- Pangkat negatif menunjukkan kebalikan dari pangkat positif. Dalam hal ini, (3/4)-2 sama dengan 1 dibagi dengan (3/4)2.
- Maka, (3/4)-2 = 1 / ((3/4) x (3/4)) = 1 / (9/16) = 16/9.
Menghitung Pangkat Pecahan dengan Kalkulator
Kalkulator dapat membantu kita menghitung pangkat pecahan dengan mudah. Berikut langkah-langkah umum yang dapat digunakan:
- Masukkan bilangan pecahan yang ingin dipangkatkan.
- Tekan tombol “^” atau “xy” pada kalkulator.
- Masukkan nilai pangkatnya.
- Tekan tombol “=” untuk mendapatkan hasil perhitungan.
Sebagai contoh, untuk menghitung (1/2)3 dengan kalkulator, kita dapat memasukkan 1/2, kemudian menekan tombol “^” atau “xy“, lalu memasukkan 3, dan terakhir menekan tombol “=”. Hasilnya akan menunjukkan 1/8.
Soal Pangkat Desimal
Dalam matematika, bilangan desimal seringkali terlibat dalam operasi pangkat. Memahami cara menghitung pangkat desimal sangat penting, terutama dalam konteks kalkulus, geometri, dan berbagai bidang lainnya. Contoh soal berikut akan menunjukkan bagaimana menghitung pangkat desimal dengan kalkulator, serta memberikan ilustrasi tentang cara mengubah bilangan desimal ke bentuk pecahan sebelum menghitung pangkat.
Contoh Soal Pangkat Desimal
Berikut ini adalah dua contoh soal pangkat yang melibatkan bilangan desimal dan langkah-langkah penyelesaiannya menggunakan kalkulator:
-
Soal 1: Hitunglah nilai dari (0,5)3.
Penyelesaian:
- Masukkan 0,5 ke dalam kalkulator.
- Tekan tombol pangkat (biasanya tombol dengan simbol “^” atau “xy“).
- Masukkan 3 sebagai eksponen.
- Tekan tombol sama dengan (=).
- Hasilnya adalah 0,125.
Jadi, (0,5)3 = 0,125.
-
Soal 2: Hitunglah nilai dari (1,2)2.
Penyelesaian:
- Masukkan 1,2 ke dalam kalkulator.
- Tekan tombol pangkat (biasanya tombol dengan simbol “^” atau “xy“).
- Masukkan 2 sebagai eksponen.
- Tekan tombol sama dengan (=).
- Hasilnya adalah 1,44.
Jadi, (1,2)2 = 1,44.
Mengubah Bilangan Desimal ke Bentuk Pecahan
Untuk menghitung pangkat desimal secara manual, kita dapat mengubah bilangan desimal ke bentuk pecahan terlebih dahulu. Berikut adalah ilustrasi cara mengubah bilangan desimal ke bentuk pecahan:
Misalnya, kita ingin mengubah 0,75 ke bentuk pecahan. Langkah-langkahnya adalah:
- Tuliskan bilangan desimal sebagai pecahan dengan penyebut 1: 0,75/1.
- Kalikan pembilang dan penyebut dengan 100 (karena ada dua angka di belakang koma): (0,75 x 100) / (1 x 100) = 75/100.
- Sederhanakan pecahan tersebut dengan mencari faktor persekutuan terbesar (FPB) dari 75 dan 100, yaitu 25: (75/25) / (100/25) = 3/4.
Jadi, 0,75 sama dengan 3/4. Setelah mengubah bilangan desimal ke bentuk pecahan, kita dapat menghitung pangkatnya dengan cara yang sama seperti menghitung pangkat pecahan biasa.
Soal Pangkat Akar
Soal pangkat yang melibatkan akar sering muncul dalam berbagai bidang, seperti matematika, fisika, dan teknik. Soal-soal ini biasanya membutuhkan pemahaman tentang sifat-sifat pangkat dan akar, serta kemampuan untuk mengoperasikan kalkulator.
Contoh Soal Pangkat Akar
Berikut adalah dua contoh soal pangkat yang melibatkan akar:
- Hitunglah nilai dari
(√2)3
- Tentukan nilai dari
(√3)-2
Langkah-langkah Penyelesaian Soal Pangkat Akar dengan Kalkulator
Berikut adalah langkah-langkah penyelesaian soal pangkat yang melibatkan akar dengan menggunakan kalkulator:
- Masuk ke mode kalkulator ilmiah.
- Tekan tombol akar kuadrat (√) dan masukkan nilai yang berada di dalam akar.
- Tekan tombol pangkat (^) dan masukkan nilai pangkat.
- Tekan tombol sama dengan (=) untuk mendapatkan hasil.
Contoh Soal Pangkat Akar dan Bilangan Pecahan
Berikut adalah contoh soal pangkat yang melibatkan akar dan bilangan pecahan:
Hitunglah nilai dari (√2/3)4
Untuk menyelesaikan soal ini, kita dapat menggunakan kalkulator ilmiah. Langkah-langkahnya sama seperti yang telah dijelaskan sebelumnya.
Soal Pangkat Variabel
Soal pangkat yang melibatkan variabel merupakan bagian penting dalam aljabar. Pemahaman tentang sifat-sifat pangkat dan operasi aljabar sangat dibutuhkan untuk menyelesaikan soal-soal ini.
Contoh Soal Pangkat Variabel
Berikut ini adalah contoh soal pangkat yang melibatkan variabel beserta langkah-langkah penyelesaiannya:
-
Sederhanakan ekspresi berikut: (2x3y2)2
Penyelesaian:
1. Gunakan sifat pangkat untuk mengalikan pangkat pada setiap faktor di dalam tanda kurung: (2x3y2)2 = 22(x3)2(y2)2
2. Hitung pangkat dari setiap faktor: 22(x3)2(y2)2 = 4x6y4
Jadi, bentuk sederhana dari (2x3y2)2 adalah 4x6y4.
-
Sederhanakan ekspresi berikut: (a2b-1)3 / (a-1b2)2
Penyelesaian:
1. Gunakan sifat pangkat untuk mengalikan pangkat pada setiap faktor di dalam tanda kurung: (a2b-1)3 / (a-1b2)2 = a6b-3 / a-2b4
2. Gunakan sifat pembagian pangkat dengan basis yang sama: a6b-3 / a-2b4 = a6-(-2)b-3-4
3. Hitung pangkat dari setiap faktor: a6-(-2)b-3-4 = a8b-7
Jadi, bentuk sederhana dari (a2b-1)3 / (a-1b2)2 adalah a8b-7.
Soal Pangkat Variabel dan Konstanta
Berikut adalah contoh soal pangkat yang melibatkan variabel dan konstanta:
Sederhanakan ekspresi berikut: (3x2y3)2 + 2(x4y6)
Penyelesaian:
1. Gunakan sifat pangkat untuk mengalikan pangkat pada setiap faktor di dalam tanda kurung: (3x2y3)2 + 2(x4y6) = 9x4y6 + 2x4y6
2. Gabungkan suku-suku sejenis: 9x4y6 + 2x4y6 = 11x4y6
Jadi, bentuk sederhana dari (3x2y3)2 + 2(x4y6) adalah 11x4y6.
Soal Pangkat Kombinasi
Soal pangkat yang melibatkan operasi kombinasi seperti penjumlahan, pengurangan, perkalian, dan pembagian mengharuskan kita untuk memahami urutan operasi matematika. Urutan operasi ini penting untuk memastikan hasil perhitungan yang benar.
Contoh Soal Pangkat Kombinasi, Contoh soal berpangkat
Berikut adalah 3 contoh soal pangkat yang menggabungkan berbagai operasi matematika, lengkap dengan langkah-langkah penyelesaiannya.
-
Hitunglah nilai dari
23 + 5 × 4 - 10 ÷ 2.Berikut langkah-langkah penyelesaiannya:
-
Hitung pangkat terlebih dahulu:
23 = 2 × 2 × 2 = 8. -
Lakukan perkalian:
5 × 4 = 20. -
Lakukan pembagian:
10 ÷ 2 = 5. -
Hitung penjumlahan dan pengurangan dari kiri ke kanan:
8 + 20 - 5 = 23.
Jadi, nilai dari
23 + 5 × 4 - 10 ÷ 2adalah23.Contoh soal berpangkat biasanya melibatkan operasi perkalian dengan basis yang sama dan eksponen yang berbeda. Misalnya, bagaimana kita menghitung 2 pangkat 3 dikalikan dengan 2 pangkat 2? Nah, kalau kamu ingin mempelajari lebih lanjut tentang konsep ekonomi, kamu bisa cek contoh soal teori produksi ekonomi mikro yang membahas tentang bagaimana perusahaan menentukan jumlah output yang optimal dengan berbagai kombinasi faktor produksi.
Setelah memahami konsep produksi, kamu bisa kembali ke contoh soal berpangkat dan menerapkannya dalam konteks ekonomi, seperti menghitung total produksi dengan berbagai skenario input.
-
-
Tentukan nilai dari
(32 - 1) × 2 ÷ 4 + 6.Langkah-langkah penyelesaiannya adalah:
-
Hitung pangkat di dalam tanda kurung:
32 = 3 × 3 = 9. -
Hitung operasi di dalam tanda kurung:
(9 - 1) = 8. -
Lakukan perkalian:
8 × 2 = 16. -
Lakukan pembagian:
16 ÷ 4 = 4. -
Hitung penjumlahan:
4 + 6 = 10.
Oleh karena itu, nilai dari
(32 - 1) × 2 ÷ 4 + 6adalah10. -
-
Hitunglah hasil dari
(52 + 23) ÷ (4 + 1).Langkah-langkah penyelesaiannya adalah:
-
Hitung pangkat di dalam tanda kurung:
52 = 5 × 5 = 25dan23 = 2 × 2 × 2 = 8. -
Hitung operasi di dalam tanda kurung:
(25 + 8) = 33dan(4 + 1) = 5. -
Lakukan pembagian:
33 ÷ 5 = 6.6.
Jadi, nilai dari
(52 + 23) ÷ (4 + 1)adalah6.6. -
Penyelesaian Soal Pangkat Kombinasi dengan Kalkulator
Kalkulator dapat membantu dalam menyelesaikan soal pangkat yang melibatkan operasi kombinasi. Kebanyakan kalkulator ilmiah memiliki tombol pangkat (biasanya dengan simbol “^” atau “xy“). Untuk menyelesaikan soal pangkat dengan kalkulator, ikuti langkah-langkah berikut:
-
Masukkan bilangan pokok (basis) yang ingin dipangkatkan.
-
Tekan tombol pangkat ( “^” atau “xy“).
-
Masukkan nilai pangkat (eksponen).
-
Tekan tombol sama dengan (=) untuk mendapatkan hasil.
Misalnya, untuk menghitung 23, masukkan 2, tekan tombol pangkat, masukkan 3, lalu tekan tombol sama dengan. Kalkulator akan menampilkan hasil 8.
Setelah menghitung pangkat, Anda dapat menggunakan kalkulator untuk menyelesaikan operasi kombinasi lainnya seperti penjumlahan, pengurangan, perkalian, dan pembagian dengan mengikuti urutan operasi yang benar.
Soal Pangkat dengan Bentuk Eksponensial
Bentuk eksponensial merupakan cara lain untuk menyatakan perkalian berulang suatu bilangan. Memahami bentuk eksponensial sangat penting dalam menyelesaikan soal pangkat, karena kita dapat memanfaatkan sifat-sifat eksponensial untuk menyederhanakan operasi hitung. Dalam artikel ini, kita akan membahas beberapa contoh soal pangkat yang melibatkan bentuk eksponensial dan bagaimana menyelesaikannya dengan menggunakan sifat-sifat eksponensial.
Contoh Soal Pangkat dengan Bentuk Eksponensial
Berikut adalah dua contoh soal pangkat yang melibatkan bentuk eksponensial:
- Contoh 1: Sederhanakan bentuk eksponensial berikut: (23)2
- Contoh 2: Hitung nilai dari 3-2 x 34
Langkah-langkah Penyelesaian Soal Pangkat dengan Bentuk Eksponensial
Untuk menyelesaikan soal pangkat dengan bentuk eksponensial, kita dapat menggunakan sifat-sifat eksponensial berikut:
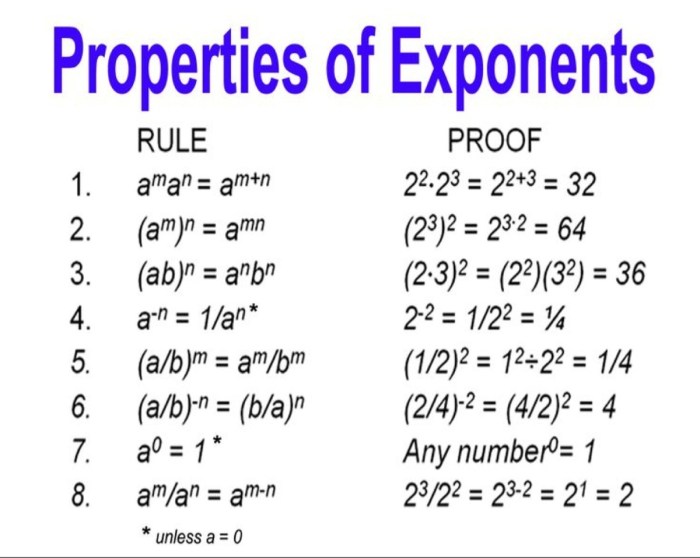
- Sifat 1: (am)n = am x n
- Sifat 2: am x an = am + n
Berikut langkah-langkah penyelesaian untuk kedua contoh soal di atas:
Contoh 1: Sederhanakan bentuk eksponensial berikut: (23)2
Menggunakan sifat 1, kita dapat menyederhanakan bentuk eksponensial tersebut:
(23)2 = 23 x 2 = 26
Jadi, bentuk sederhana dari (23)2 adalah 26.
Contoh 2: Hitung nilai dari 3-2 x 34
Menggunakan sifat 2, kita dapat menghitung nilai dari 3-2 x 34:
3-2 x 34 = 3-2 + 4 = 32 = 9
Jadi, nilai dari 3-2 x 34 adalah 9.
Soal Pangkat dengan Bentuk Eksponensial dan Variabel
Soal pangkat juga dapat melibatkan variabel. Berikut contoh soal pangkat yang melibatkan bentuk eksponensial dan variabel:
Sederhanakan bentuk eksponensial berikut: (x2y3)4
Untuk menyelesaikan soal ini, kita dapat menggunakan sifat 1 dan sifat distributif perkalian terhadap pangkat:
(x2y3)4 = x2 x 4y3 x 4 = x8y12
Jadi, bentuk sederhana dari (x2y3)4 adalah x8y12.
Soal Pangkat dalam Konteks Nyata
Konsep pangkat tidak hanya terbatas pada soal-soal matematika di buku pelajaran. Pangkat juga memiliki aplikasi luas dalam kehidupan sehari-hari, membantu kita dalam memahami dan menyelesaikan berbagai masalah.
Contohnya, dalam menghitung pertumbuhan populasi, menghitung bunga majemuk, atau menghitung volume suatu objek, pangkat memainkan peran penting. Mari kita bahas beberapa contoh soal cerita yang melibatkan penggunaan pangkat dalam kehidupan nyata.
Contoh Soal Cerita 1: Pertumbuhan Bakteri
Misalkan sebuah bakteri berkembang biak dengan cara membelah diri menjadi dua setiap jam. Jika awalnya terdapat 1 bakteri, berapa banyak bakteri yang ada setelah 5 jam?
- Pada jam pertama, terdapat 1 bakteri. Setelah membelah diri, jumlah bakteri menjadi 1 x 2 = 2 bakteri.
- Pada jam kedua, terdapat 2 bakteri. Setelah membelah diri, jumlah bakteri menjadi 2 x 2 = 22 = 4 bakteri.
- Pada jam ketiga, terdapat 4 bakteri. Setelah membelah diri, jumlah bakteri menjadi 4 x 2 = 23 = 8 bakteri.
- Dengan pola yang sama, pada jam kelima, jumlah bakteri menjadi 25 = 32 bakteri.
Jadi, setelah 5 jam, akan terdapat 32 bakteri.
Contoh Soal Cerita 2: Bunga Majemuk
Pak Ahmad menabung sebesar Rp10.000.000,- di bank dengan bunga majemuk 5% per tahun. Berapa besar tabungan Pak Ahmad setelah 3 tahun?
- Tahun pertama, bunga yang diperoleh adalah 5% dari Rp10.000.000,- yaitu 0,05 x Rp10.000.000,- = Rp500.000,-. Total tabungan Pak Ahmad menjadi Rp10.000.000,- + Rp500.000,- = Rp10.500.000,-.
- Tahun kedua, bunga yang diperoleh adalah 5% dari Rp10.500.000,- yaitu 0,05 x Rp10.500.000,- = Rp525.000,-. Total tabungan Pak Ahmad menjadi Rp10.500.000,- + Rp525.000,- = Rp11.025.000,-.
- Tahun ketiga, bunga yang diperoleh adalah 5% dari Rp11.025.000,- yaitu 0,05 x Rp11.025.000,- = Rp551.250,-. Total tabungan Pak Ahmad menjadi Rp11.025.000,- + Rp551.250,- = Rp11.576.250,-.
Dengan menggunakan konsep pangkat, kita dapat menghitung tabungan Pak Ahmad setelah 3 tahun dengan rumus:
Tabungan akhir = Tabungan awal x (1 + Bunga)Jumlah tahun
Maka, tabungan akhir Pak Ahmad adalah Rp10.000.000,- x (1 + 0,05)3 = Rp11.576.250,-.
Ringkasan Terakhir: Contoh Soal Berpangkat
Melalui berbagai contoh soal yang telah dibahas, kita dapat melihat bahwa konsep pangkat memiliki aplikasi yang luas dalam matematika. Dengan memahami sifat-sifat dan cara menyelesaikan soal pangkat, kamu akan mampu menyelesaikan masalah yang lebih kompleks dan mengembangkan pemahamanmu tentang matematika. Ingatlah, latihan adalah kunci untuk menguasai konsep ini. Semakin banyak soal yang kamu kerjakan, semakin mahir kamu dalam menggunakan pangkat untuk menyelesaikan berbagai masalah.






