Contoh Soal Bilangan Berpangkat dan Cara Penyelesaiannya Kelas 10

Contoh soal bilangan berpangkat dan cara penyelesaiannya kelas 10 – Pernahkah kamu bertanya-tanya bagaimana cara menghitung luas permukaan sebuah kotak dengan sisi yang sangat kecil? Atau bagaimana menghitung pertumbuhan populasi bakteri dalam waktu singkat? Bilangan berpangkat hadir untuk menjawab pertanyaan-pertanyaan tersebut. Bilangan berpangkat merupakan konsep matematika yang sangat penting, tidak hanya dalam ilmu pengetahuan, tetapi juga dalam kehidupan sehari-hari.

Pada artikel ini, kita akan membahas tentang contoh soal bilangan berpangkat dan cara penyelesaiannya untuk kelas 10. Kita akan mulai dengan memahami definisi bilangan berpangkat, sifat-sifatnya, dan bagaimana melakukan operasi hitung dengan bilangan berpangkat. Selanjutnya, kita akan melihat contoh soal yang melibatkan bentuk akar dan bilangan berpangkat. Di akhir artikel, kita akan membahas penerapan bilangan berpangkat dalam kehidupan sehari-hari dan memberikan contoh soal latihan untuk menguji pemahamanmu.

Pengertian Bilangan Berpangkat

Bilangan berpangkat merupakan cara singkat untuk menulis perkalian berulang dari suatu bilangan. Bilangan berpangkat terdiri dari dua bagian utama, yaitu basis dan eksponen. Basis adalah bilangan yang dikalikan berulang kali, sedangkan eksponen menunjukkan berapa kali basis dikalikan dengan dirinya sendiri.

Contoh Bilangan Berpangkat

Bilangan berpangkat dapat ditulis dengan menggunakan simbol pangkat, yaitu angka kecil yang ditempatkan di atas dan di sebelah kanan basis. Sebagai contoh, bilangan berpangkat 2³ dibaca “dua pangkat tiga”. Basisnya adalah 2 dan eksponennya adalah 3. Bilangan ini menunjukkan perkalian berulang dari 2 sebanyak 3 kali, yaitu 2 × 2 × 2 = 8.

Aturan Penulisan Bilangan Berpangkat

Berikut adalah aturan penulisan bilangan berpangkat:

• Basis ditulis terlebih dahulu, kemudian diikuti eksponen.
• Eksponen ditulis dengan angka kecil di atas dan di sebelah kanan basis.
• Jika eksponennya 1, maka hasilnya sama dengan basisnya. Misalnya, 5¹ = 5.
• Jika eksponennya 0, maka hasilnya selalu 1. Misalnya, 7⁰ = 1.
• Jika eksponennya negatif, maka bilangan berpangkat tersebut merupakan kebalikan dari bilangan berpangkat dengan eksponen positif. Misalnya, 3^-2 = 1/3² = 1/9.

Sifat-Sifat Bilangan Berpangkat

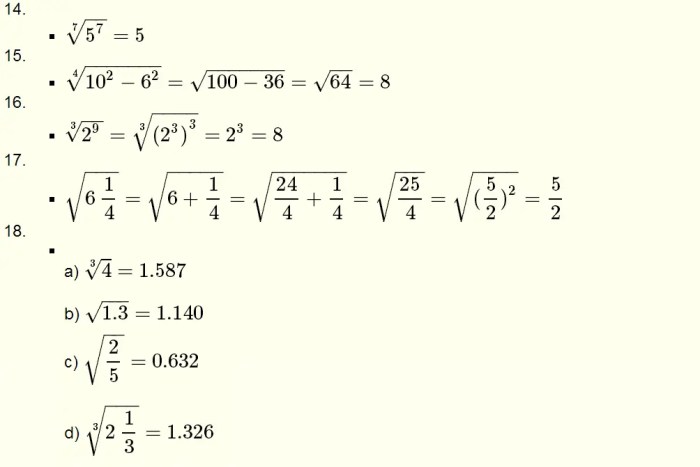
Bilangan berpangkat adalah bentuk penulisan singkat dari perkalian berulang suatu bilangan. Misalnya, 2³ sama dengan 2 x 2 x 2. Sifat-sifat bilangan berpangkat sangat penting dalam menyelesaikan berbagai soal matematika, terutama dalam aljabar dan kalkulus.

Contoh soal bilangan berpangkat kelas 10 bisa kamu temukan dengan mudah di berbagai sumber, seperti buku teks atau website pendidikan. Nah, buat kamu yang ingin latihan soal lebih menantang, bisa coba soal essay. Misalnya, soal tentang cara menghitung volume kubus dengan panjang rusuk 2 pangkat 3 cm.

Soal seperti ini akan melatih kamu untuk berpikir kritis dan mengaplikasikan konsep bilangan berpangkat dalam situasi nyata. Ingat, pemahaman konsep sangat penting, karena kamu juga bisa menemukan soal essay yang lebih kompleks seperti contoh soal essay korespondensi dan jawabannya.

Jadi, latihan terus ya agar kamu semakin mahir dalam mengerjakan soal bilangan berpangkat!

Berikut adalah beberapa sifat penting bilangan berpangkat yang akan kita bahas:

Sifat-Sifat Bilangan Berpangkat

• Sifat 1: Perkalian Bilangan Berpangkat dengan Basis Sama

  Jika basisnya sama, maka pangkatnya dijumlahkan.

  a^m x aⁿ = a^m+n

  Contoh:

  2³ x 2⁴ = 2³⁺⁴ = 2⁷

• Sifat 2: Pembagian Bilangan Berpangkat dengan Basis Sama

  Jika basisnya sama, maka pangkatnya dikurangkan.

  a^m : aⁿ = a^m-n

  Contoh:

  3⁵ : 3² = 3^5-2 = 3³

• Sifat 3: Perpangkatan Bilangan Berpangkat

  Pangkat dari bilangan berpangkat sama dengan perkalian pangkatnya.

  (a^m)ⁿ = a^{m x n}

  Contoh:

  (5²)³ = 5^{2 x 3} = 5⁶

• Sifat 4: Perkalian Bilangan Berpangkat dengan Pangkat Sama

  Jika pangkatnya sama, maka basisnya dikalikan.

  aⁿ x bⁿ = (a x b)ⁿ

  Contoh:

  2⁴ x 3⁴ = (2 x 3)⁴ = 6⁴

• Sifat 5: Pembagian Bilangan Berpangkat dengan Pangkat Sama

  Jika pangkatnya sama, maka basisnya dibagi.

  aⁿ : bⁿ = (a : b)ⁿ

  Contoh:

  8³ : 2³ = (8 : 2)³ = 4³

• Sifat 6: Bilangan Berpangkat Nol

  Setiap bilangan yang dipangkatkan dengan nol hasilnya adalah 1.

  a⁰ = 1

  Contoh:

  5⁰ = 1

• Sifat 7: Bilangan Berpangkat Negatif

  Bilangan berpangkat negatif sama dengan kebalikan dari bilangan berpangkat positif dengan basis yang sama.

  a^-n = 1/aⁿ

  Contoh:

  2^-3 = 1/2³ = 1/8

Penerapan Sifat-Sifat Bilangan Berpangkat dalam Menyelesaikan Soal

Sifat-sifat bilangan berpangkat dapat digunakan untuk menyelesaikan berbagai soal matematika, terutama soal-soal yang melibatkan perkalian, pembagian, dan perpangkatan. Berikut beberapa contoh:

• Contoh 1: Sederhanakan bentuk 2³ x 2⁵.

Menggunakan sifat 1, kita dapat menjumlahkan pangkatnya:

2³ x 2⁵ = 2³⁺⁵ = 2⁸

• Contoh 2: Sederhanakan bentuk (3²)⁴.

Menggunakan sifat 3, kita dapat mengalikan pangkatnya:

(3²)⁴ = 3^{2 x 4} = 3⁸

• Contoh 3: Hitung nilai dari 5^-2.

Menggunakan sifat 7, kita dapat mengubah pangkat negatif menjadi pangkat positif:

5^-2 = 1/5² = 1/25

Operasi pada Bilangan Berpangkat: Contoh Soal Bilangan Berpangkat Dan Cara Penyelesaiannya Kelas 10

Bilangan berpangkat merupakan cara singkat untuk menulis perkalian berulang suatu bilangan. Operasi pada bilangan berpangkat melibatkan penjumlahan, pengurangan, perkalian, dan pembagian. Operasi-operasi ini mengikuti aturan tertentu yang memanfaatkan sifat-sifat bilangan berpangkat untuk mempermudah perhitungan.

Penjumlahan dan Pengurangan Bilangan Berpangkat

Penjumlahan dan pengurangan bilangan berpangkat hanya dapat dilakukan jika bilangan pokok dan pangkatnya sama. Jika tidak, operasi tersebut tidak dapat dilakukan secara langsung.

Contoh:
– 2³ + 2³ = 2(2³) = 2(2 x 2 x 2) = 2(8) = 16
– 3² – 3² = 0

Perkalian Bilangan Berpangkat

Dalam perkalian bilangan berpangkat dengan bilangan pokok yang sama, pangkatnya dijumlahkan.

Contoh:
– 2² x 2³ = 2⁽²⁺³⁾ = 2⁵ = 2 x 2 x 2 x 2 x 2 = 32

Pembagian Bilangan Berpangkat

Dalam pembagian bilangan berpangkat dengan bilangan pokok yang sama, pangkatnya dikurangkan.

Contoh:
– 3⁵ / 3² = 3⁽⁵⁻²⁾ = 3³ = 3 x 3 x 3 = 27

Penggunaan Sifat-Sifat Bilangan Berpangkat dalam Operasi

Sifat-sifat bilangan berpangkat sangat berguna dalam menyelesaikan operasi bilangan berpangkat. Berikut beberapa sifat penting:

– (aᵐ)ⁿ = aᵐⁿ
– aᵐ x aⁿ = aᵐ⁺ⁿ
– aᵐ / aⁿ = aᵐ⁻ⁿ
– a⁰ = 1
– a⁻ⁿ = 1/aⁿ

Contoh Soal:
– Sederhanakan (2³)² x 2⁴ / 2⁵
– Solusi:
– (2³)² x 2⁴ / 2⁵ = 2⁶ x 2⁴ / 2⁵
– = 2¹⁰ / 2⁵
– = 2⁵
– = 2 x 2 x 2 x 2 x 2 = 32

Bentuk Akar dan Bilangan Berpangkat

Bilangan berpangkat dan bentuk akar adalah konsep penting dalam matematika yang saling terkait. Bilangan berpangkat menyatakan perkalian berulang dari suatu bilangan, sedangkan bentuk akar menyatakan operasi kebalikan dari bilangan berpangkat.

Hubungan Antara Bentuk Akar dan Bilangan Berpangkat

Bentuk akar dan bilangan berpangkat saling berhubungan melalui konsep invers. Jika kita memiliki bilangan berpangkat aⁿ, maka bentuk akarnya adalah ⁿ√a. Dengan kata lain, bentuk akar merupakan operasi kebalikan dari bilangan berpangkat.

Contohnya, jika kita memiliki bilangan berpangkat 2³ = 8, maka bentuk akarnya adalah ³√8 = 2. Ini menunjukkan bahwa akar pangkat tiga dari 8 adalah 2, yang merupakan kebalikan dari 2³ = 8.

Contoh Soal dan Penyelesaian

Misalkan kita memiliki soal berikut:

Sederhanakan bentuk akar ⁴√16.

Untuk menyelesaikan soal ini, kita dapat menggunakan hubungan antara bentuk akar dan bilangan berpangkat. Kita tahu bahwa ⁴√16 adalah bilangan yang jika dipangkatkan empat akan menghasilkan 16. Bilangan tersebut adalah 2, karena 2⁴ = 16. Jadi, ⁴√16 = 2.

Mengubah Bentuk Akar Menjadi Bilangan Berpangkat dan Sebaliknya, Contoh soal bilangan berpangkat dan cara penyelesaiannya kelas 10

Untuk mengubah bentuk akar menjadi bilangan berpangkat, kita dapat menggunakan rumus berikut:

ⁿ√a = a^1/n

Contohnya, ³√8 dapat diubah menjadi bilangan berpangkat 8^1/3.

Untuk mengubah bilangan berpangkat menjadi bentuk akar, kita dapat menggunakan rumus berikut:

a^m/n = ⁿ√a^m

Contohnya, 2^3/4 dapat diubah menjadi bentuk akar ⁴√2³.

Contoh Soal Bilangan Berpangkat dan Penyelesaiannya

Bilangan berpangkat merupakan salah satu materi penting dalam matematika yang sering dijumpai dalam berbagai bidang, seperti fisika, kimia, dan ekonomi. Memahami konsep bilangan berpangkat dan cara menyelesaikan soal-soal yang melibatkannya sangat penting untuk menguasai materi matematika lainnya.

Soal Bilangan Berpangkat dan Penyelesaiannya

Soal bilangan berpangkat dapat melibatkan berbagai operasi hitung, seperti penjumlahan, pengurangan, perkalian, pembagian, dan juga sifat-sifat bilangan berpangkat. Untuk menyelesaikan soal-soal bilangan berpangkat, perlu dipahami dengan baik konsep dasar bilangan berpangkat dan sifat-sifatnya.

Berikut ini contoh soal bilangan berpangkat yang melibatkan operasi hitung dan sifat-sifat bilangan berpangkat:

Contoh 1:

Sederhanakan bentuk `(2^3 * 3^2) / (2^2 * 3)`.

Penyelesaian:

1. Gunakan sifat perkalian bilangan berpangkat: `a^m * a^n = a^(m+n)`.
`2^3 * 3^2 = 2^(3+0) * 3^(2+0) = 2^3 * 3^2`
2. Gunakan sifat pembagian bilangan berpangkat: `a^m / a^n = a^(m-n)`.
`(2^3 * 3^2) / (2^2 * 3) = 2^(3-2) * 3^(2-1) = 2^1 * 3^1`
3. Hitung hasil akhirnya.
`2^1 * 3^1 = 2 * 3 = 6`

Jadi, hasil dari `(2^3 * 3^2) / (2^2 * 3)` adalah 6.

Contoh 2:

Hitung nilai dari `(5^2)^3`.

Penyelesaian:

1. Gunakan sifat pangkat dari bilangan berpangkat: `(a^m)^n = a^(m*n)`.
`(5^2)^3 = 5^(2*3) = 5^6`
2. Hitung hasil akhirnya.
`5^6 = 5 * 5 * 5 * 5 * 5 * 5 = 15625`

Jadi, nilai dari `(5^2)^3` adalah 15625.

Contoh 3:

Sederhanakan bentuk `(x^2 * y^3)^4`.

Penyelesaian:

1. Gunakan sifat pangkat dari bilangan berpangkat: `(a^m)^n = a^(m*n)`.
`(x^2 * y^3)^4 = x^(2*4) * y^(3*4) = x^8 * y^12`

Jadi, bentuk sederhana dari `(x^2 * y^3)^4` adalah `x^8 * y^12`.

Menentukan Hasil Operasi Bilangan Berpangkat dengan Kalkulator

Untuk menentukan hasil operasi bilangan berpangkat dengan menggunakan kalkulator, umumnya terdapat tombol khusus yang digunakan untuk operasi pangkat, yaitu tombol “^” atau “x^y”.

Langkah-langkah menggunakan kalkulator:

1. Masukkan bilangan pokok.
2. Tekan tombol pangkat “^” atau “x^y”.
3. Masukkan nilai pangkat.
4. Tekan tombol sama dengan “=” untuk mendapatkan hasil.

Contoh:

Untuk menghitung `2^5`, masukkan angka 2, tekan tombol “^” atau “x^y”, masukkan angka 5, lalu tekan tombol “=”. Hasilnya akan ditampilkan pada layar kalkulator, yaitu 32.

Penggunaan kalkulator sangat membantu dalam menyelesaikan soal-soal bilangan berpangkat, terutama untuk bilangan berpangkat yang besar.

Penerapan Bilangan Berpangkat dalam Kehidupan Sehari-hari

Bilangan berpangkat, meskipun tampak abstrak, memiliki peran penting dalam berbagai aspek kehidupan kita. Penerapannya meluas dari ilmu pengetahuan hingga teknologi dan ekonomi, membantu kita memahami dan menyelesaikan berbagai permasalahan kompleks.

Perhitungan Pertumbuhan Populasi

Bilangan berpangkat membantu kita dalam memahami pertumbuhan populasi secara eksponensial. Misalnya, jika populasi suatu kota meningkat sebesar 2% per tahun, kita dapat menggunakan bilangan berpangkat untuk memprediksi populasi kota tersebut di masa depan. Misalkan, jika populasi awal kota tersebut adalah 1 juta jiwa, maka setelah 10 tahun, populasi kota tersebut akan menjadi 1 juta x (1.02)^10 ≈ 1.219 juta jiwa.

Perhitungan Bunga Majemuk

Dalam dunia keuangan, bilangan berpangkat digunakan untuk menghitung bunga majemuk. Bunga majemuk adalah bunga yang dihitung atas pokok pinjaman atau tabungan ditambah bunga yang telah terkumpul sebelumnya. Rumus untuk menghitung bunga majemuk adalah:

A = P (1 + r/n)^(nt)

di mana A adalah jumlah akhir, P adalah pokok, r adalah suku bunga, n adalah jumlah kali bunga dihitung per tahun, dan t adalah waktu dalam tahun. Misalnya, jika kita menabung Rp 10 juta dengan suku bunga 5% per tahun, dihitung secara bulanan (n = 12), maka setelah 5 tahun, jumlah tabungan kita akan menjadi:

A = 10.000.000 (1 + 0.05/12)^(12 x 5) ≈ Rp 12.833.592

Perhitungan Luas Permukaan Benda

Bilangan berpangkat juga digunakan dalam menghitung luas permukaan benda, khususnya untuk benda-benda dengan bentuk geometri yang rumit. Misalnya, untuk menghitung luas permukaan kubus, kita dapat menggunakan rumus:

Luas permukaan kubus = 6 x s^2

di mana s adalah panjang sisi kubus. Rumus ini menunjukkan bahwa luas permukaan kubus sebanding dengan kuadrat dari panjang sisinya.

Soal Latihan Bilangan Berpangkat

Setelah mempelajari materi tentang bilangan berpangkat, saatnya kita menguji pemahamanmu dengan beberapa soal latihan. Soal-soal berikut ini dirancang dengan tingkat kesulitan yang berbeda, mulai dari yang mudah hingga yang lebih menantang. Yuk, kita selesaikan bersama!

Contoh Soal Latihan Bilangan Berpangkat

Berikut ini adalah lima contoh soal latihan bilangan berpangkat yang bisa kamu kerjakan untuk mengasah kemampuanmu:

1. Sederhanakan bentuk $2^3 \times 2^4$.
2. Hitunglah nilai dari $5^2 \div 5^3$.
3. Tentukan nilai dari $(3^2)^3$.
4. Sederhanakan bentuk $\fracx^5x^2$.
5. Tentukan nilai dari $x^0$, jika $x \neq 0$.

Kunci Jawaban Soal Latihan Bilangan Berpangkat

Berikut ini adalah kunci jawaban untuk soal-soal latihan di atas:

1. $2^3 \times 2^4 = 2^3+4 = 2^7 = 128$
2. $5^2 \div 5^3 = 5^2-3 = 5^-1 = \frac15$
3. $(3^2)^3 = 3^2 \times 3 = 3^6 = 729$
4. $\fracx^5x^2 = x^5-2 = x^3$
5. $x^0 = 1$, untuk $x \neq 0$.

Strategi Menyelesaikan Soal Latihan Bilangan Berpangkat

Untuk menyelesaikan soal-soal latihan bilangan berpangkat, kamu dapat menggunakan beberapa strategi berikut:

• Pahami sifat-sifat bilangan berpangkat. Sifat-sifat ini akan sangat membantu dalam menyederhanakan bentuk-bentuk bilangan berpangkat. Beberapa sifat penting yang perlu kamu ingat adalah:
• $a^m \times a^n = a^m+n$
• $a^m \div a^n = a^m-n$
• $(a^m)^n = a^m \times n$
• $a^0 = 1$ (dengan $a \neq 0$)
• Sederhanakan bentuk soal. Sebelum menghitung, cobalah untuk menyederhanakan bentuk soal terlebih dahulu dengan menggunakan sifat-sifat bilangan berpangkat.
• Hitung dengan teliti. Setelah menyederhanakan bentuk soal, hitunglah hasilnya dengan teliti. Pastikan kamu tidak melakukan kesalahan perhitungan.

Kesulitan dalam Memahami Bilangan Berpangkat

Bilangan berpangkat merupakan konsep dasar dalam matematika yang memiliki peran penting dalam berbagai bidang, seperti aljabar, kalkulus, dan statistika. Namun, banyak siswa yang mengalami kesulitan dalam memahami konsep ini. Kesulitan ini bisa muncul karena beberapa faktor, seperti kurangnya pemahaman dasar tentang perkalian, kesulitan dalam mengingat sifat-sifat bilangan berpangkat, atau kurangnya latihan soal.

Identifikasi Kesulitan Umum dalam Memahami Bilangan Berpangkat

Ada beberapa kesulitan yang sering dialami siswa dalam memahami konsep bilangan berpangkat. Berikut adalah beberapa di antaranya:

• Kesulitan dalam memahami arti pangkat: Siswa mungkin bingung dengan arti dari pangkat, seperti apa yang dimaksud dengan 2³. Mereka mungkin tidak memahami bahwa 2³ sama dengan 2 x 2 x 2.
• Kesulitan dalam mengingat sifat-sifat bilangan berpangkat: Siswa mungkin kesulitan mengingat sifat-sifat seperti a^m x aⁿ = a^m+n atau (a^m)ⁿ = a^{m x n}.
• Kesulitan dalam menerapkan konsep bilangan berpangkat dalam soal: Siswa mungkin kesulitan dalam menerapkan konsep bilangan berpangkat dalam soal cerita atau soal yang melibatkan operasi matematika lainnya.

Strategi Mengatasi Kesulitan dalam Memahami Bilangan Berpangkat

Untuk mengatasi kesulitan dalam memahami bilangan berpangkat, beberapa strategi dapat diterapkan:

• Memahami Konsep Dasar: Pastikan siswa memahami konsep dasar perkalian dan operasi matematika lainnya sebelum mempelajari bilangan berpangkat.
• Latihan Soal yang Beragam: Berikan siswa latihan soal yang beragam, mulai dari soal dasar hingga soal yang lebih kompleks.
• Visualisasi: Gunakan visualisasi untuk membantu siswa memahami konsep bilangan berpangkat. Misalnya, gunakan gambar untuk menunjukkan arti dari 2³.
• Membuat Kaitan dengan Kehidupan Sehari-hari: Buatlah contoh soal yang berhubungan dengan kehidupan sehari-hari agar siswa lebih mudah memahami konsep bilangan berpangkat. Misalnya, menghitung jumlah bakteri yang berkembang biak dengan cepat.
• Pembahasan Soal Secara Kolaboratif: Dorong siswa untuk berdiskusi dan saling membantu dalam memahami konsep bilangan berpangkat.

Contoh Soal yang Sering Menjadi Sumber Kesulitan

Salah satu contoh soal yang sering menjadi sumber kesulitan bagi siswa adalah soal yang melibatkan operasi perkalian dan pembagian bilangan berpangkat dengan basis yang sama. Misalnya:

Hitunglah nilai dari 2³ x 2⁴ : 2².

Penyelesaian

Untuk menyelesaikan soal ini, siswa perlu memahami sifat-sifat bilangan berpangkat, yaitu:

• a^m x aⁿ = a^m+n
• a^m : aⁿ = a^m-n

Dengan menggunakan sifat-sifat tersebut, kita dapat menyelesaikan soal di atas sebagai berikut:

2³ x 2⁴ : 2² = 2³⁺⁴ : 2² = 2⁷ : 2² = 2^7-2 = 2⁵ = 32.

Dengan memahami konsep dan sifat-sifat bilangan berpangkat, siswa dapat menyelesaikan soal yang lebih kompleks dengan mudah.

Aplikasi Pembelajaran Bilangan Berpangkat

Pembelajaran bilangan berpangkat, meskipun penting, bisa terasa rumit bagi sebagian siswa. Namun, dengan bantuan teknologi, proses belajar ini bisa menjadi lebih interaktif dan menyenangkan. Aplikasi pembelajaran bilangan berpangkat menawarkan berbagai fitur yang dapat membantu siswa memahami konsep dengan lebih mudah.

Aplikasi Pembelajaran Bilangan Berpangkat Online

Aplikasi pembelajaran bilangan berpangkat online dapat diakses dengan mudah melalui komputer atau perangkat mobile. Aplikasi ini biasanya menyediakan berbagai materi pembelajaran, seperti video tutorial, latihan soal, dan simulasi interaktif. Beberapa aplikasi bahkan menawarkan fitur gamifikasi untuk membuat proses belajar lebih menarik.

• Khan Academy: Platform ini menyediakan berbagai materi pembelajaran matematika, termasuk bilangan berpangkat, dalam bentuk video dan latihan soal. Khan Academy terkenal dengan materi pembelajarannya yang mudah dipahami dan dikemas dengan cara yang menarik.
• MathPapa: Aplikasi ini membantu siswa menyelesaikan soal-soal matematika, termasuk soal bilangan berpangkat, dengan langkah-langkah yang jelas dan mudah diikuti. MathPapa juga menawarkan kalkulator online yang dapat membantu siswa dalam memeriksa jawaban mereka.
• Photomath: Aplikasi ini memungkinkan siswa untuk memindai soal matematika, termasuk soal bilangan berpangkat, dengan kamera ponsel mereka. Photomath kemudian akan memberikan solusi langkah demi langkah dan penjelasan yang mudah dipahami.

Manfaat Menggunakan Aplikasi Pembelajaran Bilangan Berpangkat

Penggunaan aplikasi pembelajaran bilangan berpangkat dalam proses belajar memiliki beberapa manfaat, yaitu:

• Pembelajaran yang Interaktif: Aplikasi pembelajaran biasanya dirancang dengan fitur interaktif yang memungkinkan siswa untuk belajar dengan cara yang lebih aktif. Misalnya, dengan menggunakan simulasi, siswa dapat secara langsung melihat bagaimana konsep bilangan berpangkat bekerja.
• Akses Materi yang Lebih Luas: Aplikasi pembelajaran menyediakan akses ke berbagai materi pembelajaran yang mungkin tidak tersedia di buku teks. Ini memberikan siswa kesempatan untuk belajar dari berbagai sumber dan perspektif.
• Pengecekan dan Evaluasi yang Lebih Cepat: Aplikasi pembelajaran biasanya dilengkapi dengan fitur pengecekan jawaban dan evaluasi yang memungkinkan siswa untuk mengetahui seberapa baik pemahaman mereka terhadap materi. Hal ini membantu siswa untuk mengidentifikasi area yang perlu ditingkatkan dan mendapatkan umpan balik yang lebih cepat.

Ringkasan Terakhir

Dengan memahami konsep bilangan berpangkat, kamu akan mampu menyelesaikan berbagai masalah matematika yang melibatkan bilangan berpangkat. Kamu juga akan dapat melihat bagaimana konsep ini diterapkan dalam berbagai bidang kehidupan. Jadi, jangan ragu untuk memperdalam pemahamanmu tentang bilangan berpangkat dan nikmati manfaatnya dalam berbagai aspek kehidupan.