Contoh soal bilangan kompleks – Bilangan kompleks, sebuah konsep matematika yang memperluas dunia bilangan real dengan memasukkan bilangan imajiner, seringkali menjadi topik yang menarik sekaligus menantang. Bayangkan sebuah dunia di mana angka-angka tidak hanya mewakili besaran, tetapi juga arah dan rotasi! Dalam dunia bilangan kompleks, hal ini menjadi kenyataan.
Artikel ini akan membawa Anda menjelajahi berbagai aspek bilangan kompleks, mulai dari definisi dasar hingga aplikasi praktisnya. Dengan contoh soal yang terstruktur dan langkah-langkah yang jelas, Anda akan mendapatkan pemahaman yang lebih dalam tentang bagaimana bilangan kompleks bekerja dan bagaimana mereka dapat diterapkan dalam berbagai bidang.
Pengertian Bilangan Kompleks
Bilangan kompleks merupakan perluasan dari bilangan real yang melibatkan unit imajiner, yaitu akar kuadrat dari -1, yang dilambangkan dengan ‘i’. Bilangan kompleks memainkan peran penting dalam berbagai bidang seperti matematika, fisika, dan teknik, khususnya dalam menyelesaikan persamaan dan menganalisis sistem yang melibatkan gelombang, getaran, dan arus listrik.
Bentuk Umum Bilangan Kompleks
Bentuk umum bilangan kompleks adalah z = a + bi, di mana ‘a’ dan ‘b’ adalah bilangan real, dan ‘i’ adalah unit imajiner. ‘a’ disebut sebagai bagian real dari bilangan kompleks, sedangkan ‘b’ disebut sebagai bagian imajiner.
Contoh Bilangan Kompleks
Berikut beberapa contoh bilangan kompleks:
- 3 + 2i: Bagian real adalah 3, bagian imajiner adalah 2.
- -5 – 4i: Bagian real adalah -5, bagian imajiner adalah -4.
- 7i: Bagian real adalah 0, bagian imajiner adalah 7.
- 4: Bagian real adalah 4, bagian imajiner adalah 0.
Perbedaan Bilangan Real dan Bilangan Kompleks
Tabel berikut menunjukkan perbedaan antara bilangan real dan bilangan kompleks:
| Fitur | Bilangan Real | Bilangan Kompleks |
|---|---|---|
| Definisi | Bilangan yang dapat diplot pada garis bilangan | Bilangan yang melibatkan unit imajiner ‘i’ (√-1) |
| Bentuk Umum | ‘a’ (di mana ‘a’ adalah bilangan real) | ‘a + bi’ (di mana ‘a’ dan ‘b’ adalah bilangan real, dan ‘i’ adalah unit imajiner) |
| Contoh | 1, -2, 3.14, √2 | 3 + 2i, -5 – 4i, 7i, 4 |
| Aplikasi | Pengukuran, kalkulasi sehari-hari | Matematika tingkat tinggi, fisika, teknik |
Operasi pada Bilangan Kompleks
Bilangan kompleks, yang terdiri dari bagian real dan imajiner, dapat dioperasikan dengan cara yang mirip dengan bilangan real. Operasi-operasi dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian dapat dilakukan dengan mengikuti aturan-aturan tertentu.
Contoh soal bilangan kompleks biasanya melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian. Tapi, pernahkah kamu berpikir bagaimana bentuk grafik dari bilangan kompleks? Nah, di sini kita perlu sedikit bergeser ke topik contoh soal grafik fungsi. Misalnya, fungsi linear seperti y = 2x + 1 dapat digambarkan sebagai garis lurus.
Begitu pula, fungsi kuadrat seperti y = x^2 membentuk parabola. Nah, bagaimana dengan bilangan kompleks? Kita bisa memvisualisasikannya dalam bidang kompleks dengan sumbu real dan sumbu imajiner, sehingga menghasilkan berbagai bentuk unik yang menarik untuk dipelajari.
Penjumlahan dan Pengurangan Bilangan Kompleks
Penjumlahan dan pengurangan bilangan kompleks dilakukan dengan menjumlahkan atau mengurangi bagian real dan bagian imajiner secara terpisah.
- Misalkan kita memiliki dua bilangan kompleks, z1 = a + bi dan z2 = c + di.
- Penjumlahannya adalah z1 + z2 = (a + c) + (b + d)i.
- Pengurangannya adalah z1 – z2 = (a – c) + (b – d)i.
Contoh Soal Penjumlahan dan Pengurangan
Misalkan kita ingin menjumlahkan bilangan kompleks 3 + 2i dan 1 – 4i.
- z1 = 3 + 2i dan z2 = 1 – 4i.
- z1 + z2 = (3 + 1) + (2 – 4)i.
- z1 + z2 = 4 – 2i.
Untuk pengurangan, misalkan kita ingin mengurangi 1 – 4i dari 3 + 2i.
- z1 = 3 + 2i dan z2 = 1 – 4i.
- z1 – z2 = (3 – 1) + (2 + 4)i.
- z1 – z2 = 2 + 6i.
Perkalian Bilangan Kompleks
Perkalian bilangan kompleks dilakukan dengan menggunakan distributif property, seperti perkalian aljabar biasa.
- Misalkan kita memiliki dua bilangan kompleks, z1 = a + bi dan z2 = c + di.
- Perkaliannya adalah z1 * z2 = (a + bi)(c + di) = ac + adi + bci + bdi2.
- Karena i2 = -1, maka z1 * z2 = (ac – bd) + (ad + bc)i.
Contoh Soal Perkalian
Misalkan kita ingin mengalikan bilangan kompleks 2 + 3i dengan 4 – i.
- z1 = 2 + 3i dan z2 = 4 – i.
- z1 * z2 = (2 + 3i)(4 – i) = 8 – 2i + 12i – 3i2.
- z1 * z2 = (8 + 3) + (-2 + 12)i.
- z1 * z2 = 11 + 10i.
Pembagian Bilangan Kompleks
Pembagian bilangan kompleks dilakukan dengan mengalikan pembilang dan penyebut dengan konjugat penyebut.
- Misalkan kita memiliki dua bilangan kompleks, z1 = a + bi dan z2 = c + di.
- Pembagiannya adalah z1 / z2 = (a + bi) / (c + di).
- Konjugat dari z2 adalah c – di.
- z1 / z2 = (a + bi)(c – di) / (c + di)(c – di) = (ac + bd) + (bc – ad)i / (c2 + d2).
Contoh Soal Pembagian
Misalkan kita ingin membagi bilangan kompleks 5 + 2i dengan 1 – 3i.
- z1 = 5 + 2i dan z2 = 1 – 3i.
- z1 / z2 = (5 + 2i) / (1 – 3i).
- Konjugat dari z2 adalah 1 + 3i.
- z1 / z2 = (5 + 2i)(1 + 3i) / (1 – 3i)(1 + 3i) = (5 + 15i + 2i + 6i2) / (12 – (3i)2).
- z1 / z2 = (-1 + 17i) / (1 + 9) = (-1 + 17i) / 10.
- z1 / z2 = -1/10 + 17/10i.
Tabel Rumus Operasi Bilangan Kompleks
| Operasi | Rumus |
|---|---|
| Penjumlahan | (a + bi) + (c + di) = (a + c) + (b + d)i |
| Pengurangan | (a + bi) – (c + di) = (a – c) + (b – d)i |
| Perkalian | (a + bi)(c + di) = (ac – bd) + (ad + bc)i |
| Pembagian | (a + bi) / (c + di) = (ac + bd) + (bc – ad)i / (c2 + d2) |
Bentuk Polar Bilangan Kompleks: Contoh Soal Bilangan Kompleks
Bilangan kompleks dapat dinyatakan dalam dua bentuk, yaitu bentuk kartesius dan bentuk polar. Bentuk kartesius adalah representasi bilangan kompleks dalam bentuk *a + bi*, di mana *a* dan *b* adalah bilangan real, dan *i* adalah satuan imajiner (√-1). Bentuk polar, di sisi lain, menggunakan sudut dan jarak dari titik asal sebagai representasi bilangan kompleks. Bentuk polar sangat berguna dalam operasi seperti perkalian dan pembagian bilangan kompleks.
Mengubah Bilangan Kompleks dari Bentuk Kartesius ke Bentuk Polar
Untuk mengubah bilangan kompleks dari bentuk kartesius *a + bi* ke bentuk polar *r(cos θ + i sin θ)*, kita perlu menentukan nilai *r* (modulus) dan *θ* (argumen). Modulus *r* mewakili jarak dari titik asal ke titik yang mewakili bilangan kompleks di bidang kompleks. Argumen *θ* mewakili sudut antara sumbu real positif dan garis yang menghubungkan titik asal dengan titik yang mewakili bilangan kompleks.
Berikut adalah langkah-langkah untuk mengubah bilangan kompleks dari bentuk kartesius ke bentuk polar:
- Tentukan modulus *r*: Modulus *r* dihitung dengan menggunakan rumus:
*r* = √( *a*2 + *b*2)
- Tentukan argumen *θ*: Argumen *θ* dihitung dengan menggunakan rumus:
*θ* = arctan (*b*/ *a*)
Perhatikan bahwa rumus ini hanya berlaku untuk kuadran I dan IV. Untuk kuadran lainnya, perlu penyesuaian sudut berdasarkan posisi titik yang mewakili bilangan kompleks di bidang kompleks.
- Tulis bentuk polar: Setelah mendapatkan nilai *r* dan *θ*, bilangan kompleks dapat ditulis dalam bentuk polar:
*r*(cos *θ* + *i* sin *θ*)
Contoh Soal
Ubah bilangan kompleks 3 + 4*i* dari bentuk kartesius ke bentuk polar.
Langkah 1: Tentukan modulus *r*
*r* = √(32 + 42) = √(9 + 16) = √25 = 5
Langkah 2: Tentukan argumen *θ*
*θ* = arctan (4/3) ≈ 53.13°
Langkah 3: Tulis bentuk polar
Bentuk polar dari 3 + 4*i* adalah:
5(cos 53.13° + *i* sin 53.13°)
Tabel Hubungan Bentuk Kartesius dan Bentuk Polar
Berikut adalah tabel yang menunjukkan hubungan antara bentuk kartesius dan bentuk polar bilangan kompleks:
| Bentuk Kartesius | Bentuk Polar |
|---|---|
| *a + bi* | *r*(cos *θ* + *i* sin *θ*) |
| *a* | *a*(cos 0° + *i* sin 0°) |
| *bi* | *b*(cos 90° + *i* sin 90°) |
| – *a* | *a*(cos 180° + *i* sin 180°) |
| – *bi* | *b*(cos 270° + *i* sin 270°) |
Operasi pada Bentuk Polar
Setelah mempelajari cara mengubah bilangan kompleks dari bentuk kartesius ke bentuk polar dan sebaliknya, sekarang saatnya kita bahas operasi perkalian dan pembagian bilangan kompleks dalam bentuk polar. Bentuk polar ternyata memberikan cara yang lebih sederhana untuk melakukan operasi perkalian dan pembagian dibandingkan dengan bentuk kartesius. Yuk, kita pelajari bersama!
Perkalian Bilangan Kompleks dalam Bentuk Polar
Perkalian bilangan kompleks dalam bentuk polar sangat mudah. Kita hanya perlu mengalikan modulus kedua bilangan kompleks dan menjumlahkan argumennya.
- Misalkan kita memiliki dua bilangan kompleks dalam bentuk polar:
$z_1 = r_1 (\cos \theta_1 + i \sin \theta_1)$
$z_2 = r_2 (\cos \theta_2 + i \sin \theta_2)$ - Maka, hasil perkalian kedua bilangan kompleks tersebut adalah:
$z_1 \cdot z_2 = r_1 r_2 [\cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2)]$
Contoh Soal Perkalian
Misalkan kita ingin mengalikan dua bilangan kompleks berikut:
- $z_1 = 2 (\cos 30^\circ + i \sin 30^\circ)$
- $z_2 = 3 (\cos 60^\circ + i \sin 60^\circ)$
Langkah-langkahnya adalah:
- Kalikan modulus kedua bilangan kompleks: $2 \cdot 3 = 6$.
- Jumlahkan argumen kedua bilangan kompleks: $30^\circ + 60^\circ = 90^\circ$.
- Hasil perkaliannya adalah: $z_1 \cdot z_2 = 6 (\cos 90^\circ + i \sin 90^\circ)$.
Pembagian Bilangan Kompleks dalam Bentuk Polar
Pembagian bilangan kompleks dalam bentuk polar juga mudah. Kita hanya perlu membagi modulus kedua bilangan kompleks dan mengurangkan argumennya.
- Misalkan kita memiliki dua bilangan kompleks dalam bentuk polar:
$z_1 = r_1 (\cos \theta_1 + i \sin \theta_1)$
$z_2 = r_2 (\cos \theta_2 + i \sin \theta_2)$ - Maka, hasil pembagian kedua bilangan kompleks tersebut adalah:
$z_1 / z_2 = (r_1 / r_2) [\cos (\theta_1 – \theta_2) + i \sin (\theta_1 – \theta_2)]$
Contoh Soal Pembagian
Misalkan kita ingin membagi dua bilangan kompleks berikut:
- $z_1 = 4 (\cos 120^\circ + i \sin 120^\circ)$
- $z_2 = 2 (\cos 30^\circ + i \sin 30^\circ)$
Langkah-langkahnya adalah:
- Bagi modulus kedua bilangan kompleks: $4 / 2 = 2$.
- Kurangkan argumen kedua bilangan kompleks: $120^\circ – 30^\circ = 90^\circ$.
- Hasil pembagiannya adalah: $z_1 / z_2 = 2 (\cos 90^\circ + i \sin 90^\circ)$.
Rumus Operasi Bilangan Kompleks dalam Bentuk Polar
| Operasi | Rumus |
|---|---|
| Perkalian | $z_1 \cdot z_2 = r_1 r_2 [\cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2)]$ |
| Pembagian | $z_1 / z_2 = (r_1 / r_2) [\cos (\theta_1 – \theta_2) + i \sin (\theta_1 – \theta_2)]$ |
Aplikasi Bilangan Kompleks
Bilangan kompleks, yang terdiri dari bagian real dan imajiner, memiliki peran penting dalam berbagai bidang, melampaui matematika murni. Kemampuannya untuk merepresentasikan besaran yang melibatkan fase dan amplitudo membuatnya sangat berguna dalam fisika, teknik, dan ilmu komputer.
Aplikasi dalam Matematika
Bilangan kompleks memiliki aplikasi luas dalam matematika, khususnya dalam:
- Teori Fungsi: Bilangan kompleks merupakan alat penting dalam memahami dan menganalisis fungsi kompleks, yang melibatkan variabel kompleks. Konsep seperti integral kompleks dan residu memiliki aplikasi dalam berbagai bidang, seperti fisika dan teknik.
- Aljabar Linier: Bilangan kompleks digunakan dalam aljabar linier untuk mempelajari matriks dan transformasi linear. Contohnya, nilai eigen dari matriks dapat berupa bilangan kompleks, dan transformasi linear dapat direpresentasikan menggunakan bilangan kompleks.
- Teori Bilangan: Bilangan kompleks digunakan dalam teori bilangan untuk mempelajari sifat-sifat bilangan bulat dan bilangan rasional. Contohnya, teorema bilangan prima menyatakan bahwa setiap bilangan bulat positif dapat ditulis sebagai hasil kali bilangan prima.
Aplikasi dalam Fisika, Contoh soal bilangan kompleks
Bilangan kompleks sangat berguna dalam fisika, terutama dalam:
- Elektromagnetisme: Bilangan kompleks digunakan untuk merepresentasikan medan elektromagnetik yang berosilasi. Misalnya, arus bolak-balik (AC) dapat direpresentasikan menggunakan bilangan kompleks, yang memungkinkan analisis dan perhitungan yang lebih mudah.
- Mekanika Kuantum: Bilangan kompleks memainkan peran penting dalam mekanika kuantum. Fungsi gelombang, yang menggambarkan keadaan suatu partikel, adalah fungsi kompleks. Operator kuantum juga sering kali direpresentasikan sebagai bilangan kompleks.
- Gelombang dan Osilasi: Bilangan kompleks digunakan untuk menganalisis gelombang dan osilasi. Misalnya, gelombang elektromagnetik dapat direpresentasikan menggunakan bilangan kompleks, yang memungkinkan analisis dan perhitungan yang lebih mudah.
Aplikasi dalam Teknik
Bilangan kompleks memiliki aplikasi luas dalam berbagai bidang teknik, termasuk:
- Teknik Elektro: Bilangan kompleks digunakan untuk menganalisis dan mendesain rangkaian listrik. Contohnya, impedansi suatu rangkaian listrik dapat direpresentasikan menggunakan bilangan kompleks, yang memungkinkan analisis dan perhitungan yang lebih mudah.
- Teknik Sipil: Bilangan kompleks digunakan untuk menganalisis dan mendesain struktur bangunan. Contohnya, getaran struktur dapat direpresentasikan menggunakan bilangan kompleks, yang memungkinkan analisis dan perhitungan yang lebih mudah.
- Teknik Kimia: Bilangan kompleks digunakan untuk menganalisis dan mendesain proses kimia. Contohnya, reaksi kimia dapat direpresentasikan menggunakan bilangan kompleks, yang memungkinkan analisis dan perhitungan yang lebih mudah.
Tabel Aplikasi Bilangan Kompleks
| Bidang | Aplikasi | Contoh |
|---|---|---|
| Matematika | Teori Fungsi, Aljabar Linier, Teori Bilangan | Integral kompleks, nilai eigen matriks, teorema bilangan prima |
| Fisika | Elektromagnetisme, Mekanika Kuantum, Gelombang dan Osilasi | Arus bolak-balik, fungsi gelombang, gelombang elektromagnetik |
| Teknik | Teknik Elektro, Teknik Sipil, Teknik Kimia | Impedansi rangkaian listrik, getaran struktur, reaksi kimia |
Bilangan Kompleks dan Geometri
Bilangan kompleks, yang terdiri dari bagian real dan imajiner, memiliki hubungan erat dengan geometri. Representasi geometri bilangan kompleks memungkinkan kita untuk memvisualisasikan dan memahami operasi aljabar bilangan kompleks dengan cara yang lebih intuitif.
Representasi Geometri Bilangan Kompleks
Setiap bilangan kompleks dapat direpresentasikan sebagai titik pada bidang kompleks. Bidang kompleks terdiri dari sumbu horizontal (sumbu real) dan sumbu vertikal (sumbu imajiner). Bilangan kompleks *z = a + bi* diwakili oleh titik dengan koordinat (a, b), di mana *a* adalah bagian real dan *b* adalah bagian imajiner.
Contoh Soal
Misalnya, bilangan kompleks *z = 3 + 4i* diwakili oleh titik (3, 4) pada bidang kompleks. Titik ini terletak 3 satuan ke kanan dari titik asal (0, 0) pada sumbu real dan 4 satuan ke atas pada sumbu imajiner.
Hubungan Bilangan Kompleks dan Geometri
| Konsep Bilangan Kompleks | Konsep Geometri |
|---|---|
| Penjumlahan bilangan kompleks | Penjumlahan vektor |
| Perkalian bilangan kompleks | Rotasi dan dilatasi vektor |
| Modul bilangan kompleks | Panjang vektor |
| Argumen bilangan kompleks | Sudut vektor terhadap sumbu real |
Soal Latihan Bilangan Kompleks
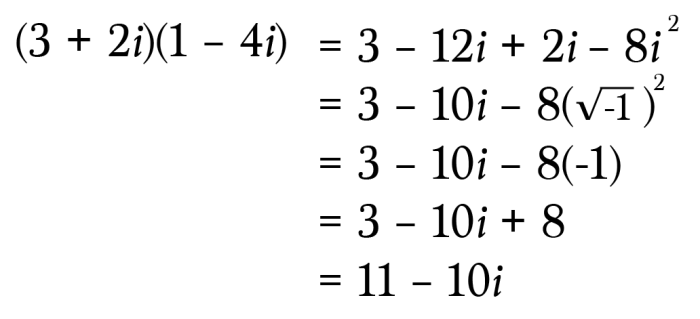
Bilangan kompleks merupakan konsep penting dalam matematika yang memiliki aplikasi luas dalam berbagai bidang seperti fisika, teknik, dan ilmu komputer. Untuk memahami konsep ini dengan lebih baik, latihan soal merupakan cara yang efektif.
Berikut adalah 5 contoh soal latihan bilangan kompleks yang mencakup berbagai topik, disertai dengan kunci jawabannya. Soal-soal ini dirancang untuk membantu Anda memahami konsep dasar bilangan kompleks dan mengasah kemampuan Anda dalam menyelesaikan operasi aljabar yang melibatkan bilangan kompleks.
Operasi Dasar Bilangan Kompleks
Soal-soal berikut menguji pemahaman Anda tentang operasi dasar bilangan kompleks seperti penjumlahan, pengurangan, perkalian, dan pembagian.
- Tentukan hasil dari operasi penjumlahan berikut: (2 + 3i) + (4 – 5i).
- Tentukan hasil dari operasi pengurangan berikut: (7 – 2i) – (3 + 4i).
- Tentukan hasil dari operasi perkalian berikut: (1 + i) * (2 – 3i).
- Tentukan hasil dari operasi pembagian berikut: (5 + 2i) / (1 – i).
| Soal | Kunci Jawaban |
|---|---|
| (2 + 3i) + (4 – 5i) | 6 – 2i |
| (7 – 2i) – (3 + 4i) | 4 – 6i |
| (1 + i) * (2 – 3i) | 5 – i |
| (5 + 2i) / (1 – i) | (3 + 7i)/2 |
Bentuk Polar Bilangan Kompleks
Soal-soal berikut menguji pemahaman Anda tentang konversi bilangan kompleks dari bentuk kartesius ke bentuk polar dan sebaliknya.
- Tentukan bentuk polar dari bilangan kompleks 3 + 4i.
- Tentukan bentuk kartesius dari bilangan kompleks 5∠30°.
| Soal | Kunci Jawaban |
|---|---|
| Bentuk polar dari 3 + 4i | 5∠53.1° |
| Bentuk kartesius dari 5∠30° | 4.33 + 2.5i |
Teorema De Moivre
Soal-soal berikut menguji pemahaman Anda tentang teorema De Moivre yang menyatakan bahwa untuk setiap bilangan kompleks z dalam bentuk polar dan setiap bilangan bulat n, maka zn = rn∠nθ.
- Tentukan hasil dari (2∠30°)3.
| Soal | Kunci Jawaban |
|---|---|
| (2∠30°)3 | 8∠90° |
Akar Bilangan Kompleks
Soal-soal berikut menguji pemahaman Anda tentang cara menentukan akar dari bilangan kompleks.
- Tentukan akar kuadrat dari bilangan kompleks 4i.
| Soal | Kunci Jawaban |
|---|---|
| Akar kuadrat dari 4i | 2∠45° dan 2∠225° |
Persamaan Kuadrat dengan Koefisien Kompleks
Soal-soal berikut menguji pemahaman Anda tentang cara menyelesaikan persamaan kuadrat dengan koefisien kompleks.
- Tentukan akar-akar dari persamaan kuadrat z2 + (1 + i)z + i = 0.
| Soal | Kunci Jawaban |
|---|---|
| Akar-akar dari z2 + (1 + i)z + i = 0 | z = -i dan z = -1 |
Soal Ujian Bilangan Kompleks
Bilangan kompleks adalah topik penting dalam matematika yang memiliki aplikasi luas dalam berbagai bidang seperti fisika, teknik, dan ilmu komputer. Untuk menguji pemahaman siswa tentang konsep bilangan kompleks, soal ujian yang menantang sangat diperlukan. Berikut ini adalah contoh soal ujian bilangan kompleks yang dapat digunakan untuk menguji kemampuan siswa dalam menyelesaikan masalah yang melibatkan operasi bilangan kompleks, bentuk polar, dan teorema de Moivre.
Contoh Soal Ujian
Berikut ini adalah contoh soal ujian bilangan kompleks yang menantang:
- Tentukan hasil dari operasi berikut: (2 + 3i) * (4 – i) + (1 + 2i)2.
- Tentukan bentuk polar dari bilangan kompleks z = -2 + 2√3i.
- Hitunglah akar pangkat tiga dari bilangan kompleks z = 8i menggunakan teorema de Moivre.
Kunci Jawaban
Berikut adalah kunci jawaban untuk soal ujian bilangan kompleks yang telah diberikan:
| Soal | Kunci Jawaban |
|---|---|
| (2 + 3i) * (4 – i) + (1 + 2i)2 | (2 + 3i) * (4 – i) + (1 + 2i)2 = (8 + 12i – 2i – 3i2) + (1 + 4i + 4i2) = (8 + 10i + 3) + (1 + 4i – 4) = 12 + 14i |
| z = -2 + 2√3i | |z| = √((-2)2 + (2√3)2) = √(4 + 12) = 4 θ = arctan(2√3 / -2) = arctan(-√3) = -60° Maka bentuk polar dari z adalah 4(cos(-60°) + i sin(-60°)) |
| z = 8i | |z| = √(02 + 82) = 8 θ = arctan(8 / 0) = 90° Maka bentuk polar dari z adalah 8(cos(90°) + i sin(90°)) Akar pangkat tiga dari z dapat dihitung menggunakan teorema de Moivre: z1/3 = 81/3(cos((90° + 360°k)/3) + i sin((90° + 360°k)/3)) Untuk k = 0, z1/3 = 2(cos(30°) + i sin(30°)) Untuk k = 1, z1/3 = 2(cos(150°) + i sin(150°)) Untuk k = 2, z1/3 = 2(cos(270°) + i sin(270°)) |
Ringkasan Terakhir
Memahami bilangan kompleks membuka pintu menuju pemahaman yang lebih mendalam tentang matematika dan aplikasinya dalam dunia nyata. Dari menyelesaikan persamaan kuadrat hingga memahami perilaku gelombang elektromagnetik, bilangan kompleks memainkan peran penting dalam berbagai bidang ilmu pengetahuan dan teknologi.





