Contoh soal bilangan kompleks bentuk polar – Bilangan kompleks bentuk polar, seperti namanya, merupakan representasi bilangan kompleks dalam bentuk polar. Bentuk ini sangat berguna dalam berbagai bidang, terutama dalam teknik elektro dan fisika. Bentuk polar memberikan cara yang lebih intuitif untuk memahami dan menghitung operasi pada bilangan kompleks, khususnya dalam hal rotasi dan skala.

Dalam artikel ini, kita akan menjelajahi dunia bilangan kompleks bentuk polar. Kita akan mempelajari bagaimana mengubah bentuk kartesius ke bentuk polar, melakukan operasi hitung pada bilangan kompleks bentuk polar, dan melihat contoh-contoh aplikasi dalam berbagai bidang. Siap untuk menjelajahi? Mari kita mulai!

Table of Contents:

Konversi Bentuk Kartesius ke Bentuk Polar

Setelah memahami bentuk polar dan bentuk kartesius, kita perlu memahami bagaimana mengubah bentuk kartesius ke bentuk polar. Konversi ini penting karena memungkinkan kita untuk menyelesaikan berbagai masalah matematika yang melibatkan bilangan kompleks dengan lebih mudah, khususnya dalam bidang seperti kalkulus dan geometri.

Contoh soal bilangan kompleks bentuk polar biasanya melibatkan operasi seperti penjumlahan, pengurangan, perkalian, dan pembagian. Jika kamu ingin mengasah kemampuan logika visual, kamu bisa mencoba mengerjakan contoh soal tes iq gambar dan jawabannya. Meskipun berbeda, keduanya membutuhkan kemampuan analisis dan pemecahan masalah.

Setelah mencoba soal tes iq gambar, kamu bisa kembali fokus pada contoh soal bilangan kompleks bentuk polar dan memahami konsep-konsepnya dengan lebih baik.

Rumus Konversi

Untuk mengubah bilangan kompleks dari bentuk kartesius (a + bi) ke bentuk polar (r(cos θ + i sin θ)), kita perlu menggunakan rumus berikut:

Bentuk Kartesius	Bentuk Polar
a	r cos θ
b	r sin θ
r	√(a² + b²)
θ	arctan(b/a)

Langkah-Langkah Konversi

Untuk mengubah bentuk kartesius ke bentuk polar, ikuti langkah-langkah berikut:

Tentukan nilai a dan b dari bentuk kartesius (a + bi).
Hitung nilai r menggunakan rumus r = √(a² + b²).
Hitung nilai θ menggunakan rumus θ = arctan(b/a). Pastikan untuk memilih sudut θ yang tepat berdasarkan kuadran tempat bilangan kompleks berada.
Ganti nilai r dan θ ke dalam bentuk polar (r(cos θ + i sin θ)).

Contoh Konversi

Misalkan kita ingin mengubah bilangan kompleks 3 + 4i dari bentuk kartesius ke bentuk polar. Kita dapat mengikuti langkah-langkah di atas:

a = 3 dan b = 4.
r = √(3² + 4²) = √25 = 5.
θ = arctan(4/3) ≈ 53.13°. Karena bilangan kompleks berada di kuadran I, maka θ = 53.13°.
Bentuk polar dari 3 + 4i adalah 5(cos 53.13° + i sin 53.13°).

Ilustrasi Diagram, Contoh soal bilangan kompleks bentuk polar

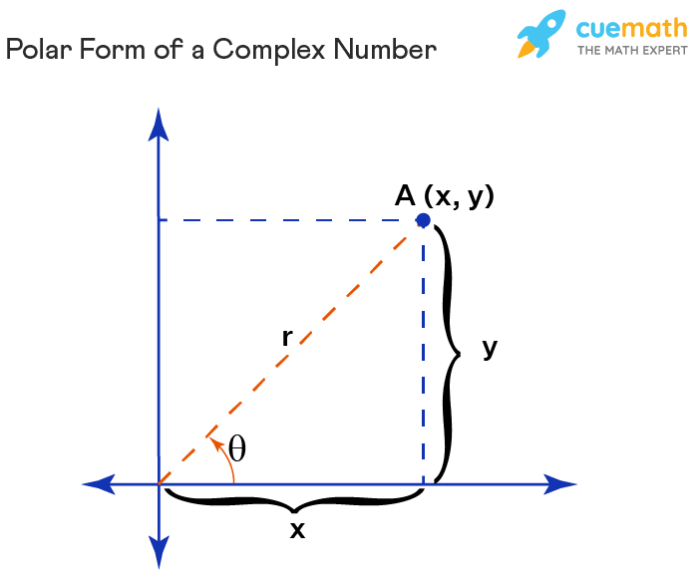
Diagram berikut menunjukkan hubungan antara bentuk kartesius dan bentuk polar dari bilangan kompleks. Titik (a, b) pada diagram mewakili bentuk kartesius a + bi. Titik ini juga dapat direpresentasikan dalam bentuk polar sebagai (r, θ), di mana r adalah jarak dari titik ke titik asal dan θ adalah sudut antara sumbu x positif dan garis yang menghubungkan titik asal dengan titik tersebut.

Diagram menunjukkan bahwa titik (a, b) dapat dicapai dengan bergerak sejauh r unit dari titik asal, kemudian memutar sudut θ searah jarum jam dari sumbu x positif. Ini adalah cara lain untuk memahami bagaimana bentuk kartesius dan bentuk polar saling berhubungan.

Operasi Hitung pada Bilangan Kompleks Bentuk Polar

Setelah memahami bagaimana mengubah bilangan kompleks dari bentuk kartesius ke bentuk polar dan sebaliknya, sekarang saatnya kita membahas operasi hitung pada bilangan kompleks bentuk polar. Bentuk polar menawarkan cara yang lebih mudah dan efisien untuk melakukan operasi perkalian dan pembagian, dibandingkan dengan bentuk kartesius. Mari kita bahas lebih lanjut.

Penjumlahan dan Pengurangan Bilangan Kompleks Bentuk Polar

Untuk melakukan penjumlahan dan pengurangan bilangan kompleks dalam bentuk polar, kita perlu mengubahnya terlebih dahulu ke bentuk kartesius. Hal ini karena penjumlahan dan pengurangan bilangan kompleks dilakukan dengan menjumlahkan atau mengurangkan komponen real dan komponen imajinernya. Bentuk polar tidak memungkinkan kita untuk melakukan operasi ini secara langsung.

Perkalian dan Pembagian Bilangan Kompleks Bentuk Polar

Perkalian dan pembagian bilangan kompleks bentuk polar jauh lebih mudah dibandingkan dengan bentuk kartesius. Berikut adalah rumusnya:

Perkalian: Jika $z_1 = r_1 (\cos \theta_1 + i \sin \theta_1)$ dan $z_2 = r_2 (\cos \theta_2 + i \sin \theta_2)$, maka:

$z_1 \cdot z_2 = r_1 \cdot r_2 (\cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2))$
Pembagian: Jika $z_1 = r_1 (\cos \theta_1 + i \sin \theta_1)$ dan $z_2 = r_2 (\cos \theta_2 + i \sin \theta_2)$, maka:

$z_1 / z_2 = (r_1 / r_2) (\cos (\theta_1 – \theta_2) + i \sin (\theta_1 – \theta_2))$

Contoh Soal Operasi Hitung pada Bilangan Kompleks Bentuk Polar

Mari kita lihat contoh soal untuk memperjelas operasi hitung pada bilangan kompleks bentuk polar.

Contoh 1: Perkalian

Misalkan kita memiliki dua bilangan kompleks dalam bentuk polar:

$z_1 = 2 (\cos 30^\circ + i \sin 30^\circ)$
$z_2 = 3 (\cos 60^\circ + i \sin 60^\circ)$

Untuk mengalikan $z_1$ dan $z_2$, kita gunakan rumus perkalian:

$z_1 \cdot z_2 = 2 \cdot 3 (\cos (30^\circ + 60^\circ) + i \sin (30^\circ + 60^\circ))$
$z_1 \cdot z_2 = 6 (\cos 90^\circ + i \sin 90^\circ)$
$z_1 \cdot z_2 = 6 (0 + i)$
$z_1 \cdot z_2 = 6i$

Contoh 2: Pembagian

Misalkan kita memiliki dua bilangan kompleks dalam bentuk polar:

$z_1 = 5 (\cos 120^\circ + i \sin 120^\circ)$
$z_2 = 2 (\cos 45^\circ + i \sin 45^\circ)$

Untuk membagi $z_1$ dengan $z_2$, kita gunakan rumus pembagian:

$z_1 / z_2 = (5 / 2) (\cos (120^\circ – 45^\circ) + i \sin (120^\circ – 45^\circ))$
$z_1 / z_2 = 2.5 (\cos 75^\circ + i \sin 75^\circ)$

Penerapan Bilangan Kompleks Bentuk Polar: Contoh Soal Bilangan Kompleks Bentuk Polar

Bilangan kompleks bentuk polar menawarkan cara yang elegan dan efisien untuk menyelesaikan berbagai masalah dalam bidang teknik elektro dan fisika. Bentuk polar, yang menyatakan bilangan kompleks dalam hal magnitudo dan sudut, memberikan representasi yang intuitif untuk fenomena periodik seperti arus bolak-balik (AC) dan gelombang elektromagnetik.

Teknik Elektro

Dalam teknik elektro, bilangan kompleks bentuk polar sangat berguna untuk menganalisis sirkuit AC. Bentuk polar memudahkan representasi dan manipulasi impedansi, yang merupakan resistensi terhadap arus AC yang bergantung pada frekuensi.

Impedansi komponen sirkuit, seperti resistor, kapasitor, dan induktor, dapat dinyatakan sebagai bilangan kompleks dalam bentuk polar.
Dengan menggunakan bentuk polar, kita dapat dengan mudah menghitung impedansi total sirkuit, arus yang mengalir, dan tegangan pada setiap komponen.
Bentuk polar juga memudahkan kita dalam memahami fase antara arus dan tegangan dalam sirkuit AC, yang penting untuk menentukan daya yang diserap oleh sirkuit.

Fisika

Dalam fisika, bilangan kompleks bentuk polar digunakan untuk menggambarkan gelombang elektromagnetik, yang merupakan kombinasi dari medan listrik dan magnet yang saling tegak lurus dan merambat melalui ruang.

Bentuk polar memungkinkan kita untuk mewakili amplitudo dan fase gelombang elektromagnetik, yang penting untuk memahami perilaku gelombang tersebut.
Bentuk polar juga digunakan dalam analisis gelombang cahaya, di mana gelombang cahaya dapat dianggap sebagai gelombang elektromagnetik dengan frekuensi tertentu.
Dalam mekanika kuantum, bilangan kompleks bentuk polar digunakan untuk menggambarkan fungsi gelombang partikel, yang menggambarkan probabilitas menemukan partikel di suatu titik dalam ruang.

Contoh Soal

Teknik Elektro

Misalkan sebuah sirkuit AC terdiri dari resistor 100 ohm, kapasitor 100 mikrofarad, dan induktor 100 milihenry. Sirkuit tersebut dihubungkan dengan sumber tegangan AC dengan frekuensi 50 Hz. Hitung impedansi total sirkuit dan arus yang mengalir melalui sirkuit.

Fisika

Misalkan sebuah gelombang elektromagnetik merambat dalam ruang bebas dengan frekuensi 100 MHz. Amplitudo medan listrik gelombang tersebut adalah 10 volt per meter. Tentukan bentuk polar dari gelombang elektromagnetik tersebut.

Soal Latihan Bilangan Kompleks Bentuk Polar

Setelah memahami konsep bilangan kompleks bentuk polar, mari kita praktikkan dengan mengerjakan soal latihan. Soal latihan ini akan membantu Anda mengasah pemahaman dan kemampuan dalam mengonversi bentuk kartesius ke bentuk polar, melakukan operasi hitung pada bilangan kompleks bentuk polar, dan memahami aplikasi bilangan kompleks bentuk polar dalam berbagai bidang.

Konversi Bentuk Kartesius ke Bentuk Polar

Konversi bentuk kartesius ke bentuk polar melibatkan penentuan modulus dan argumen dari bilangan kompleks. Modulus merupakan jarak dari titik yang mewakili bilangan kompleks ke titik asal, sedangkan argumen adalah sudut yang dibentuk oleh sumbu real positif dan garis yang menghubungkan titik asal dengan titik yang mewakili bilangan kompleks.

Tentukan bentuk polar dari bilangan kompleks z = 3 + 4i.
Konversi bilangan kompleks z = -2 – 2i ke bentuk polar.
Cari bentuk polar dari bilangan kompleks z = 5i.
Tentukan bentuk polar dari bilangan kompleks z = -1 + √3i.
Konversi bilangan kompleks z = -√3 – i ke bentuk polar.

Operasi Hitung pada Bilangan Kompleks Bentuk Polar

Operasi hitung pada bilangan kompleks bentuk polar dapat dilakukan dengan menggunakan rumus yang melibatkan modulus dan argumen. Penjumlahan dan pengurangan pada bilangan kompleks bentuk polar lebih mudah dilakukan dengan mengubahnya ke bentuk kartesius terlebih dahulu.

Hitunglah hasil dari perkalian bilangan kompleks z₁ = 2(cos 30° + i sin 30°) dan z₂ = 3(cos 60° + i sin 60°).
Tentukan hasil bagi dari bilangan kompleks z₁ = 4(cos 45° + i sin 45°) dan z₂ = 2(cos 15° + i sin 15°).
Hitunglah hasil dari pemangkatan bilangan kompleks z = 2(cos 60° + i sin 60°) pangkat 3.
Tentukan akar kuadrat dari bilangan kompleks z = 9(cos 120° + i sin 120°).
Hitunglah hasil dari penjumlahan bilangan kompleks z₁ = 3(cos 45° + i sin 45°) dan z₂ = 2(cos 135° + i sin 135°).

Aplikasi Bilangan Kompleks Bentuk Polar

Bilangan kompleks bentuk polar memiliki aplikasi yang luas dalam berbagai bidang, seperti:

Teknik Elektro: Bilangan kompleks bentuk polar digunakan untuk menganalisis rangkaian listrik AC. Modulus mewakili amplitudo arus atau tegangan, sedangkan argumen mewakili fase. Contohnya, dalam analisis rangkaian AC, impedansi suatu komponen dapat direpresentasikan sebagai bilangan kompleks bentuk polar.
Fisika: Bilangan kompleks bentuk polar digunakan untuk menggambarkan gelombang, seperti gelombang elektromagnetik dan gelombang suara. Modulus mewakili amplitudo gelombang, sedangkan argumen mewakili fase gelombang.
Komputer Grafis: Bilangan kompleks bentuk polar digunakan untuk rotasi dan skala objek dalam ruang dua dimensi. Modulus mewakili faktor skala, sedangkan argumen mewakili sudut rotasi.
Matematika: Bilangan kompleks bentuk polar digunakan untuk menyelesaikan persamaan trigonometri dan persamaan diferensial. Bentuk polar memudahkan dalam melakukan operasi hitung dan analisis.
Signal Processing: Bilangan kompleks bentuk polar digunakan untuk menganalisis dan memanipulasi sinyal. Modulus mewakili amplitudo sinyal, sedangkan argumen mewakili fase sinyal.

Penjelasan Rumus Trigonometri dalam Bilangan Kompleks

Bilangan kompleks dalam bentuk polar memungkinkan kita untuk merepresentasikan bilangan kompleks dengan menggunakan besaran (magnitudo) dan sudut. Rumus trigonometri memainkan peran penting dalam konversi antara bentuk kartesius dan bentuk polar, serta dalam operasi hitung bilangan kompleks bentuk polar.

Konversi Bentuk Kartesius ke Bentuk Polar

Untuk mengonversi bilangan kompleks dari bentuk kartesius (a + bi) ke bentuk polar (r∠θ), kita menggunakan rumus trigonometri berikut:

Besaran (r) dihitung menggunakan teorema Pythagoras:

r = √(a² + b²)

Sudut (θ) dihitung menggunakan fungsi tangen:

θ = arctan(b/a)

Perhatikan bahwa sudut θ harus ditentukan berdasarkan kuadran tempat bilangan kompleks berada dalam diagram Argand.

Operasi Hitung Bilangan Kompleks Bentuk Polar

Rumus trigonometri juga digunakan dalam operasi hitung bilangan kompleks bentuk polar, seperti perkalian, pembagian, dan perpangkatan.

Perkalian: Untuk mengalikan dua bilangan kompleks bentuk polar, kita kalikan besarannya dan jumlahkan sudutnya:

(r₁∠θ₁) × (r₂∠θ₂) = (r₁ × r₂)∠(θ₁ + θ₂)

Pembagian: Untuk membagi dua bilangan kompleks bentuk polar, kita bagi besarannya dan kurangi sudutnya:

(r₁∠θ₁) ÷ (r₂∠θ₂) = (r₁ ÷ r₂)∠(θ₁ – θ₂)

Perpangkatan: Untuk memangkatkan bilangan kompleks bentuk polar, kita pangkatkan besarannya dan kalikan sudutnya dengan pangkat tersebut:

(r∠θ)ⁿ = rⁿ∠(nθ)

Contoh Soal

Misalkan kita ingin mengalikan dua bilangan kompleks berikut:

z₁ = 3 + 4i dan z₂ = 2 – i

Pertama, kita konversi kedua bilangan kompleks ke bentuk polar:

z₁ = 5∠53.13°
z₂ = √5∠-26.57°

Kemudian, kita kalikan kedua bilangan kompleks tersebut dalam bentuk polar:

z₁ × z₂ = (5 × √5)∠(53.13° – 26.57°) = 5√5∠26.56°

Jadi, hasil perkalian z₁ dan z₂ adalah 5√5∠26.56°.

Simpulan Akhir

Memahami bilangan kompleks bentuk polar membuka pintu ke berbagai aplikasi dalam bidang teknik, fisika, dan matematika. Dengan menguasai konsep ini, kita dapat menyelesaikan masalah yang lebih kompleks dan mendapatkan pemahaman yang lebih mendalam tentang berbagai fenomena.

Contoh Soal Bilangan Kompleks Bentuk Polar: Panduan Lengkap