Contoh soal bilangan pecahan berpangkat – Bilangan pecahan berpangkat mungkin terdengar rumit, tapi sebenarnya konsepnya sederhana dan sering muncul dalam berbagai bidang, seperti matematika, fisika, dan ekonomi. Bayangkan Anda ingin menghitung luas sebuah lingkaran dengan jari-jari setengah meter. Anda akan menggunakan rumus luas lingkaran, yaitu πr², dengan r adalah jari-jari. Nah, dalam kasus ini, jari-jari adalah ½ meter, sehingga luasnya adalah π(½)². Rumus ini melibatkan bilangan pecahan berpangkat.
Melalui artikel ini, kita akan menjelajahi dunia bilangan pecahan berpangkat, mulai dari pengertian, sifat, operasi, hingga penerapannya dalam kehidupan sehari-hari. Dengan contoh-contoh yang mudah dipahami dan langkah-langkah yang jelas, Anda akan mampu memahami konsep ini dengan lebih baik dan menyelesaikan soal-soal yang berkaitan dengannya.
Pengertian Bilangan Pecahan Berpangkat
Bilangan pecahan berpangkat adalah bilangan pecahan yang dikalikan dengan dirinya sendiri sebanyak pangkat yang ditentukan. Pangkat menunjukkan berapa kali bilangan pecahan tersebut dikalikan dengan dirinya sendiri. Bilangan pecahan berpangkat sering digunakan dalam berbagai bidang seperti matematika, fisika, dan teknik.
Contoh Bilangan Pecahan Berpangkat
Berikut adalah contoh bilangan pecahan berpangkat:
- (1/2)3 = (1/2) x (1/2) x (1/2) = 1/8
- (3/4)2 = (3/4) x (3/4) = 9/16
- (2/5)4 = (2/5) x (2/5) x (2/5) x (2/5) = 16/625
Bilangan pecahan berpangkat dibaca dengan menyebutkan bilangan pecahannya terlebih dahulu, diikuti dengan kata “pangkat” dan angka pangkatnya. Misalnya, (1/2)3 dibaca “satu per dua pangkat tiga”.
Tabel Contoh Bilangan Pecahan Berpangkat
Berikut adalah tabel yang berisi contoh bilangan pecahan berpangkat dengan berbagai nilai pangkat:
| Bilangan Pecahan | Pangkat | Hasil |
|---|---|---|
| 1/2 | 1 | 1/2 |
| 1/2 | 2 | 1/4 |
| 1/2 | 3 | 1/8 |
| 1/2 | 4 | 1/16 |
| 3/4 | 1 | 3/4 |
| 3/4 | 2 | 9/16 |
| 3/4 | 3 | 27/64 |
| 3/4 | 4 | 81/256 |
Sifat-Sifat Bilangan Pecahan Berpangkat
Bilangan pecahan berpangkat merupakan bilangan yang memiliki pangkat dan basis berupa pecahan. Sifat-sifat bilangan pecahan berpangkat sangat penting untuk memahami dan menyelesaikan operasi matematika yang melibatkan bilangan pecahan berpangkat.
Sifat-Sifat Bilangan Pecahan Berpangkat
Berikut adalah beberapa sifat-sifat penting dari bilangan pecahan berpangkat:
- Sifat 1: (a/b)m = am / bm, dengan a ≠ 0 dan b ≠ 0.
- Sifat 2: (a/b)m / (a/b)n = (a/b)m-n, dengan a ≠ 0 dan b ≠ 0.
- Sifat 3: (a/b)m * (a/b)n = (a/b)m+n, dengan a ≠ 0 dan b ≠ 0.
- Sifat 4: (a/b)0 = 1, dengan a ≠ 0 dan b ≠ 0.
- Sifat 5: (a/b)-m = (b/a)m, dengan a ≠ 0 dan b ≠ 0.
Tabel Rumus Sifat Bilangan Pecahan Berpangkat
| Sifat | Rumus |
|---|---|
| Sifat 1 | (a/b)m = am / bm |
| Sifat 2 | (a/b)m / (a/b)n = (a/b)m-n |
| Sifat 3 | (a/b)m * (a/b)n = (a/b)m+n |
| Sifat 4 | (a/b)0 = 1 |
| Sifat 5 | (a/b)-m = (b/a)m |
Contoh Penerapan Sifat Bilangan Pecahan Berpangkat
Misalkan kita ingin menghitung (2/3)3 * (2/3)2. Kita dapat menggunakan sifat 3 untuk menyelesaikannya:
(2/3)3 * (2/3)2 = (2/3)3+2 = (2/3)5 = 32/243
Jadi, hasil dari (2/3)3 * (2/3)2 adalah 32/243.
Operasi Bilangan Pecahan Berpangkat
Bilangan pecahan berpangkat merupakan kombinasi dari konsep pecahan dan pangkat. Operasi pada bilangan pecahan berpangkat melibatkan aturan-aturan khusus yang perlu dipahami agar dapat menyelesaikan perhitungan dengan tepat.
Penjumlahan dan Pengurangan Bilangan Pecahan Berpangkat
Penjumlahan dan pengurangan bilangan pecahan berpangkat hanya dapat dilakukan jika kedua bilangan memiliki basis dan pangkat yang sama. Jika basis dan pangkatnya sama, kita dapat langsung menjumlahkan atau mengurangkan numeraturnya.
- Contoh Soal: Hitunglah 2/32 + 1/32
Langkah 1: Karena basis dan pangkatnya sama, kita dapat langsung menjumlahkan numeraturnya.
Langkah 2: (2 + 1)/32 = 3/32
Langkah 3: 3/32 = 1/3
Jadi, 2/32 + 1/32 = 1/3
Perkalian Bilangan Pecahan Berpangkat
Perkalian bilangan pecahan berpangkat dilakukan dengan mengalikan numeraturnya dan mengalikan penyebutnya. Jika basisnya sama, pangkatnya dijumlahkan.
- Contoh Soal: Hitunglah (2/5)3 x (2/5)2
Langkah 1: Karena basisnya sama, kita dapat menjumlahkan pangkatnya.
Langkah 2: (2/5)3+2 = (2/5)5
Langkah 3: (2/5)5 = 32/3125
Jadi, (2/5)3 x (2/5)2 = 32/3125
Pembagian Bilangan Pecahan Berpangkat
Pembagian bilangan pecahan berpangkat dilakukan dengan membagi numeraturnya dan membagi penyebutnya. Jika basisnya sama, pangkatnya dikurangi.
Contoh soal bilangan pecahan berpangkat biasanya melibatkan operasi matematika seperti perkalian, pembagian, dan perpangkatan. Nah, untuk memahami lebih dalam tentang operasi tersebut, kita bisa menghubungkannya dengan konsep fungsi. Misalnya, jika kita ingin mencari nilai dari (1/2)^3, kita bisa menggunakan fungsi f(x) = x^3, dengan x = 1/2.
Untuk memahami lebih lanjut tentang fungsi, kamu bisa melihat contoh soal di situs ini. Dengan mempelajari fungsi, kita bisa lebih mudah menyelesaikan soal-soal yang melibatkan bilangan pecahan berpangkat.
- Contoh Soal: Hitunglah (3/4)4 : (3/4)2
Langkah 1: Karena basisnya sama, kita dapat mengurangkan pangkatnya.
Langkah 2: (3/4)4-2 = (3/4)2
Langkah 3: (3/4)2 = 9/16
Jadi, (3/4)4 : (3/4)2 = 9/16
Penyelesaian Soal Bilangan Pecahan Berpangkat
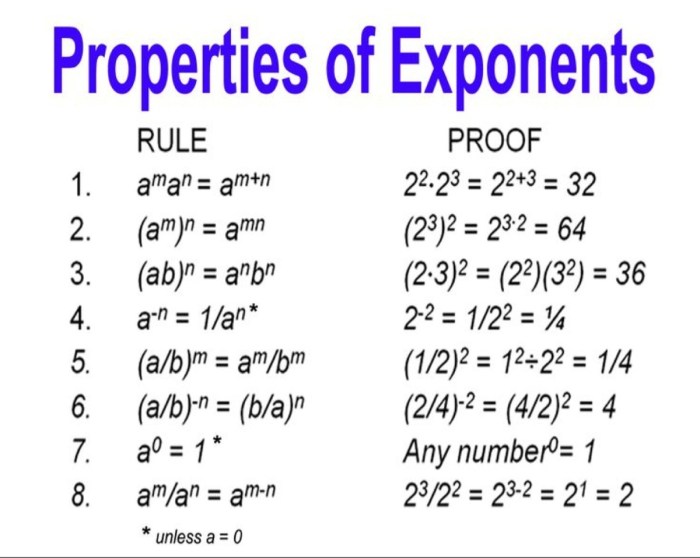
Bilangan pecahan berpangkat merupakan bilangan yang memiliki pangkat dan basis berupa pecahan. Untuk menyelesaikan soal yang melibatkan bilangan pecahan berpangkat, kita perlu memahami konsep dasar bilangan berpangkat dan operasi pecahan.
Contoh Soal dan Penyelesaian, Contoh soal bilangan pecahan berpangkat
Berikut ini contoh soal bilangan pecahan berpangkat yang melibatkan berbagai operasi dan langkah-langkah penyelesaiannya:
Soal: Hitunglah nilai dari (2/3)3 * (3/4)2.
Penyelesaian:
- Hitung nilai (2/3)3. (2/3)3 = (2/3) * (2/3) * (2/3) = 8/27.
- Hitung nilai (3/4)2. (3/4)2 = (3/4) * (3/4) = 9/16.
- Kalikan hasil dari langkah 1 dan 2. (8/27) * (9/16) = 1/6.
Jadi, nilai dari (2/3)3 * (3/4)2 adalah 1/6.
Langkah-langkah Penyelesaian Soal Bilangan Pecahan Berpangkat
| Langkah | Penjelasan |
|---|---|
| 1. Pahami Konsep Bilangan Berpangkat | Ingat bahwa an = a * a * a … (dikalikan sebanyak n kali). |
| 2. Sederhanakan Pecahan | Jika perlu, sederhanakan pecahan yang ada dalam soal. |
| 3. Hitung Nilai Pangkat | Hitung nilai pangkat untuk setiap pecahan. |
| 4. Lakukan Operasi yang Diperlukan | Lakukan operasi yang diminta dalam soal, seperti perkalian, pembagian, penjumlahan, atau pengurangan. |
| 5. Sederhanakan Hasil | Sederhanakan hasil akhir jika memungkinkan. |
Penerapan Bilangan Pecahan Berpangkat: Contoh Soal Bilangan Pecahan Berpangkat
Bilangan pecahan berpangkat, yang merupakan kombinasi dari bilangan pecahan dan eksponen, memiliki peran penting dalam berbagai bidang ilmu pengetahuan dan kehidupan sehari-hari. Penerapannya tidak hanya terbatas pada matematika, tetapi juga meluas ke fisika, ekonomi, dan bidang lainnya. Pemahaman tentang konsep ini membantu kita dalam menganalisis dan menyelesaikan berbagai masalah kompleks yang dihadapi dalam kehidupan nyata.
Penerapan dalam Kehidupan Sehari-hari
Bilangan pecahan berpangkat hadir dalam berbagai aspek kehidupan kita, meskipun kita mungkin tidak menyadarinya. Berikut adalah beberapa contohnya:
- Perhitungan Bunga Majemuk: Bunga majemuk merupakan bunga yang dihitung berdasarkan saldo pokok ditambah bunga yang telah terkumpul sebelumnya. Rumus bunga majemuk melibatkan bilangan pecahan berpangkat, di mana suku bunga dinyatakan sebagai pecahan dan dikalikan dengan jumlah pokok yang dipangkatkan dengan waktu. Contohnya, jika kita menabung Rp1.000.000 dengan suku bunga 5% per tahun selama 5 tahun, maka bunga majemuk yang diperoleh dapat dihitung menggunakan rumus:
Rp1.000.000 x (1 + 0.05)^5 = Rp1.276.281,56
- Pertumbuhan Populasi: Bilangan pecahan berpangkat juga digunakan dalam model matematika untuk memprediksi pertumbuhan populasi. Misalnya, jika populasi suatu spesies meningkat sebesar 10% setiap tahun, maka pertumbuhan populasi setelah 10 tahun dapat dihitung menggunakan rumus:
Populasi awal x (1 + 0.1)^10
- Reduksi Ukuran: Bilangan pecahan berpangkat dapat digunakan untuk menggambarkan reduksi ukuran suatu objek. Misalnya, jika kita memperkecil foto sebesar 1/2, maka ukurannya akan menjadi 1/2^2 atau 1/4 dari ukuran aslinya.
Penerapan dalam Matematika
Bilangan pecahan berpangkat memiliki peran penting dalam berbagai bidang matematika, seperti:
- Aljabar: Dalam aljabar, bilangan pecahan berpangkat digunakan untuk menyederhanakan operasi matematika yang melibatkan pecahan dan eksponen. Contohnya, (x/y)^n dapat disederhanakan menjadi x^n/y^n.
- Kalkulus: Bilangan pecahan berpangkat digunakan dalam kalkulus untuk menghitung turunan dan integral dari fungsi yang melibatkan pecahan dan eksponen.
- Teori Bilangan: Bilangan pecahan berpangkat digunakan dalam teori bilangan untuk mempelajari sifat-sifat bilangan bulat dan bilangan rasional. Misalnya, teorema Fermat terakhir membahas tentang persamaan x^n + y^n = z^n, di mana n adalah bilangan bulat positif dan x, y, dan z adalah bilangan bulat positif.
Penerapan dalam Fisika
Bilangan pecahan berpangkat juga digunakan dalam berbagai bidang fisika, seperti:
- Mekanika: Bilangan pecahan berpangkat digunakan untuk menghitung kecepatan, percepatan, dan gaya yang bekerja pada suatu benda. Misalnya, rumus untuk menghitung energi kinetik suatu benda adalah 1/2mv^2, di mana m adalah massa benda dan v adalah kecepatannya.
- Elektromagnetisme: Bilangan pecahan berpangkat digunakan untuk menghitung kuat arus, tegangan, dan hambatan dalam rangkaian listrik. Misalnya, rumus untuk menghitung daya listrik adalah P = IV, di mana P adalah daya, I adalah kuat arus, dan V adalah tegangan.
- Fisika Kuantum: Bilangan pecahan berpangkat digunakan dalam fisika kuantum untuk mempelajari sifat-sifat partikel subatomik. Misalnya, rumus untuk menghitung probabilitas menemukan partikel di suatu lokasi tertentu melibatkan bilangan pecahan berpangkat.
Penerapan dalam Ekonomi
Bilangan pecahan berpangkat juga digunakan dalam berbagai bidang ekonomi, seperti:
- Pertumbuhan Ekonomi: Bilangan pecahan berpangkat digunakan untuk menghitung tingkat pertumbuhan ekonomi. Misalnya, jika pertumbuhan ekonomi suatu negara adalah 5% per tahun, maka pertumbuhan ekonomi setelah 10 tahun dapat dihitung menggunakan rumus:
PDB tahun awal x (1 + 0.05)^10
- Analisis Investasi: Bilangan pecahan berpangkat digunakan untuk menghitung nilai investasi di masa depan. Misalnya, jika kita menginvestasikan Rp1.000.000 dengan suku bunga 10% per tahun selama 5 tahun, maka nilai investasi di masa depan dapat dihitung menggunakan rumus:
Rp1.000.000 x (1 + 0.1)^5 = Rp1.610.510
- Teori Konsumen: Bilangan pecahan berpangkat digunakan dalam teori konsumen untuk menganalisis preferensi konsumen dan bagaimana mereka memilih barang dan jasa. Misalnya, fungsi utilitas konsumen seringkali didefinisikan sebagai fungsi pangkat dari kuantitas barang dan jasa yang dikonsumsi.
Jenis-Jenis Soal Bilangan Pecahan Berpangkat
Bilangan pecahan berpangkat merupakan salah satu materi penting dalam matematika. Soal-soal yang berkaitan dengan bilangan pecahan berpangkat sering muncul dalam ujian, baik di sekolah maupun dalam seleksi masuk perguruan tinggi. Memahami jenis-jenis soal yang sering muncul dan strategi penyelesaiannya dapat membantu kamu meraih hasil yang optimal dalam ujian.
Soal Operasi Hitung Bilangan Pecahan Berpangkat
Soal operasi hitung bilangan pecahan berpangkat melibatkan penjumlahan, pengurangan, perkalian, dan pembagian bilangan pecahan berpangkat. Jenis soal ini menguji pemahaman kamu tentang aturan operasi hitung bilangan berpangkat.
- Contoh Soal: Hitunglah hasil dari (1/2)3 + (2/3)2.
- Strategi: Gunakan aturan operasi hitung bilangan berpangkat, yaitu pangkatkan terlebih dahulu bilangan pecahannya, kemudian baru lakukan operasi penjumlahan.
Soal Penyederhanaan Bilangan Pecahan Berpangkat
Soal penyederhanaan bilangan pecahan berpangkat menuntut kamu untuk menyederhanakan bentuk bilangan pecahan berpangkat menjadi bentuk yang lebih sederhana. Soal ini menguji pemahaman kamu tentang sifat-sifat bilangan berpangkat.
- Contoh Soal: Sederhanakan bentuk (2/3)4 x (3/2)2.
- Strategi: Gunakan sifat-sifat bilangan berpangkat seperti (a/b)m = am/bm dan (a/b)m x (a/b)n = (a/b)m+n untuk menyederhanakan bentuk tersebut.
Soal Persamaan Bilangan Pecahan Berpangkat
Soal persamaan bilangan pecahan berpangkat melibatkan persamaan yang mengandung bilangan pecahan berpangkat. Jenis soal ini menguji kemampuan kamu dalam menyelesaikan persamaan dan manipulasi aljabar.
- Contoh Soal: Tentukan nilai x yang memenuhi persamaan (1/2)x = 1/8.
- Strategi: Ubah kedua ruas persamaan ke dalam bentuk yang sama, kemudian selesaikan persamaan dengan menggunakan sifat-sifat bilangan berpangkat.
Soal Pertidaksamaan Bilangan Pecahan Berpangkat
Soal pertidaksamaan bilangan pecahan berpangkat melibatkan pertidaksamaan yang mengandung bilangan pecahan berpangkat. Jenis soal ini menguji kemampuan kamu dalam menyelesaikan pertidaksamaan dan manipulasi aljabar.
- Contoh Soal: Tentukan nilai x yang memenuhi pertidaksamaan (1/3)x > 1/9.
- Strategi: Ubah kedua ruas pertidaksamaan ke dalam bentuk yang sama, kemudian selesaikan pertidaksamaan dengan menggunakan sifat-sifat bilangan berpangkat.
Soal Aplikasi Bilangan Pecahan Berpangkat
Soal aplikasi bilangan pecahan berpangkat merupakan soal yang menerapkan konsep bilangan pecahan berpangkat dalam konteks kehidupan nyata. Jenis soal ini menguji kemampuan kamu dalam memahami dan menerapkan konsep matematika dalam berbagai situasi.
- Contoh Soal: Sebuah bakteri berkembang biak dengan kecepatan (1/2)n kali lipat setiap jam. Jika awalnya terdapat 100 bakteri, berapa banyak bakteri setelah 3 jam?
- Strategi: Gunakan konsep bilangan pecahan berpangkat untuk menghitung jumlah bakteri setelah 3 jam.
Kesalahan Umum dalam Menyelesaikan Soal Bilangan Pecahan Berpangkat
Bilangan pecahan berpangkat seringkali menjadi momok bagi sebagian siswa. Walaupun konsepnya tidak terlalu sulit, namun kesalahan dalam memahami dan menerapkan aturannya dapat menyebabkan hasil yang salah. Artikel ini akan membahas beberapa kesalahan umum yang sering dilakukan dalam menyelesaikan soal bilangan pecahan berpangkat dan bagaimana cara menghindarinya.
Kesalahan dalam Menentukan Basis dan Pangkat
Kesalahan pertama yang sering terjadi adalah salah menentukan basis dan pangkat. Basis adalah bilangan yang akan dikalikan dengan dirinya sendiri sebanyak pangkat yang ditentukan. Misalnya, pada bilangan pecahan (2/3)2, basisnya adalah (2/3) dan pangkatnya adalah 2.
- Kesalahan: Menentukan basis sebagai 2 dan pangkat sebagai 3.
- Penyebab: Kurangnya pemahaman tentang definisi basis dan pangkat dalam bilangan pecahan.
- Cara Menghindari: Pastikan untuk memahami definisi basis dan pangkat dalam bilangan pecahan. Ingat bahwa basis adalah seluruh bilangan pecahan, bukan hanya pembilang atau penyebutnya.
Kesalahan dalam Mengalikan Pangkat
Kesalahan umum lainnya adalah salah dalam mengalikan pangkat. Saat mengalikan pangkat, pangkatnya dikalikan, bukan dijumlahkan.
- Kesalahan: (2/3)2 x (2/3)3 = (2/3)5
- Penyebab: Kesalahan dalam mengingat aturan perkalian pangkat.
- Cara Menghindari: Ingatlah bahwa saat mengalikan pangkat, pangkatnya dikalikan. (2/3)2 x (2/3)3 = (2/3)(2+3) = (2/3)5.
Kesalahan dalam Membagi Pangkat
Saat membagi pangkat, pangkatnya dikurangi, bukan dibagi.
- Kesalahan: (2/3)5 / (2/3)2 = (2/3)2,5
- Penyebab: Kesalahan dalam mengingat aturan pembagian pangkat.
- Cara Menghindari: Ingatlah bahwa saat membagi pangkat, pangkatnya dikurangi. (2/3)5 / (2/3)2 = (2/3)(5-2) = (2/3)3.
Kesalahan dalam Menentukan Pangkat Negatif
Pangkat negatif pada bilangan pecahan menunjukkan kebalikan dari bilangan pecahan tersebut.
- Kesalahan: (2/3)-2 = – (2/3)2
- Penyebab: Kesalahan dalam memahami konsep pangkat negatif.
- Cara Menghindari: Ingatlah bahwa pangkat negatif menunjukkan kebalikan dari bilangan pecahan tersebut. (2/3)-2 = (3/2)2.
Kesalahan dalam Menentukan Pangkat Nol
Setiap bilangan berpangkat nol sama dengan 1, termasuk bilangan pecahan.
- Kesalahan: (2/3)0 = 0
- Penyebab: Kesalahan dalam memahami konsep pangkat nol.
- Cara Menghindari: Ingatlah bahwa setiap bilangan berpangkat nol sama dengan 1. (2/3)0 = 1.
Tips dan Trik Menyelesaikan Soal Bilangan Pecahan Berpangkat
Bilangan pecahan berpangkat memang terlihat rumit, tapi jangan khawatir! Dengan beberapa tips dan trik, kamu bisa mengatasinya dengan mudah. Nah, berikut adalah beberapa tips dan trik yang bisa kamu gunakan untuk menyelesaikan soal bilangan pecahan berpangkat dengan cepat dan tepat.
Memahami Konsep Dasar
Sebelum membahas tips dan trik, pastikan kamu memahami konsep dasar bilangan pecahan berpangkat. Bilangan pecahan berpangkat merupakan bentuk perkalian berulang dari suatu bilangan pecahan. Misalnya, (2/3)4 = (2/3) x (2/3) x (2/3) x (2/3). Dengan memahami konsep dasar ini, kamu akan lebih mudah dalam menyelesaikan soal.
Menerapkan Sifat-Sifat Bilangan Berpangkat
Ada beberapa sifat bilangan berpangkat yang bisa kamu manfaatkan untuk menyelesaikan soal dengan lebih mudah. Berikut beberapa contohnya:
- (a/b)n = an/bn
- (a/b)m x (a/b)n = (a/b)m+n
- (a/b)m / (a/b)n = (a/b)m-n
Menyederhanakan Pecahan
Sebelum melakukan operasi perpangkatan, kamu bisa menyederhanakan pecahan terlebih dahulu. Misalnya, (4/8)2 bisa disederhanakan menjadi (1/2)2. Dengan menyederhanakan pecahan, kamu akan mendapatkan hasil yang lebih mudah dihitung.
Menggunakan Kalkulator
Untuk soal yang lebih kompleks, kamu bisa menggunakan kalkulator. Pastikan kalkulator yang kamu gunakan mendukung operasi bilangan pecahan berpangkat. Dengan menggunakan kalkulator, kamu bisa mendapatkan hasil yang akurat dan lebih cepat.
Membuat Tabel
Kamu bisa membuat tabel untuk membantu menyelesaikan soal bilangan pecahan berpangkat. Tabel ini bisa berisi beberapa contoh soal dan langkah-langkah penyelesaiannya. Dengan membuat tabel, kamu bisa lebih mudah memahami konsep dan mempraktikkan tips dan trik yang telah dipelajari.
| Soal | Langkah Penyelesaian | Hasil |
|---|---|---|
| (2/3)3 | (2/3) x (2/3) x (2/3) = 8/27 | 8/27 |
| (1/2)4 x (1/2)2 | (1/2)4+2 = (1/2)6 = 1/64 | 1/64 |
Latihan Soal Bilangan Pecahan Berpangkat
Bilangan pecahan berpangkat merupakan salah satu materi dalam matematika yang cukup menantang. Untuk menguasai materi ini, diperlukan latihan yang cukup. Berikut ini adalah beberapa contoh soal bilangan pecahan berpangkat yang bisa kamu coba.
Contoh Soal Bilangan Pecahan Berpangkat
Berikut ini adalah lima contoh soal bilangan pecahan berpangkat yang mencakup berbagai tingkat kesulitan:
- Hitunglah nilai dari (1/2)3.
- Sederhanakan bentuk (2/3)-2.
- Tentukan nilai dari (3/4)2 x (2/3)3.
- Hitunglah nilai dari (1/5)-1 + (2/3)2.
- Sederhanakan bentuk (a/b)m x (b/a)n.
Kunci Jawaban
Berikut adalah kunci jawaban untuk setiap soal di atas:
| No | Soal | Kunci Jawaban |
|---|---|---|
| 1 | Hitunglah nilai dari (1/2)3. | (1/2)3 = (1/2) x (1/2) x (1/2) = 1/8 |
| 2 | Sederhanakan bentuk (2/3)-2. | (2/3)-2 = (3/2)2 = (3/2) x (3/2) = 9/4 |
| 3 | Tentukan nilai dari (3/4)2 x (2/3)3. | (3/4)2 x (2/3)3 = (9/16) x (8/27) = 1/6 |
| 4 | Hitunglah nilai dari (1/5)-1 + (2/3)2. | (1/5)-1 + (2/3)2 = 5 + 4/9 = 49/9 |
| 5 | Sederhanakan bentuk (a/b)m x (b/a)n. | (a/b)m x (b/a)n = (am/bm) x (bn/an) = a(m-n)/b(m-n) = (a/b)(m-n) |
Referensi dan Sumber Belajar
Untuk mempelajari lebih lanjut tentang bilangan pecahan berpangkat, kamu bisa memanfaatkan berbagai referensi dan sumber belajar yang tersedia. Berikut beberapa sumber belajar yang bisa kamu manfaatkan untuk meningkatkan pemahamanmu.
Buku Teks Matematika
Buku teks matematika yang membahas tentang bilangan pecahan berpangkat merupakan sumber belajar yang sangat baik. Buku-buku ini biasanya memberikan penjelasan yang sistematis dan lengkap, disertai contoh soal dan latihan yang dapat membantu kamu memahami konsep dan mengasah kemampuanmu.
- Matematika untuk SMA/MA Kelas X oleh Erlangga
- Matematika SMA/MA Kelas X oleh Yudhistira
- Matematika untuk SMA/MA Kelas X oleh Gramedia
Website dan Platform Pembelajaran Online
Berbagai website dan platform pembelajaran online menyediakan materi tentang bilangan pecahan berpangkat secara gratis atau berbayar. Platform-platform ini biasanya menawarkan berbagai fitur, seperti video pembelajaran, latihan soal, dan forum diskusi yang dapat membantu kamu belajar dengan lebih interaktif.
- Khan Academy: Platform pembelajaran online yang menyediakan materi matematika, termasuk tentang bilangan pecahan berpangkat, secara gratis. Khan Academy menyediakan video pembelajaran, latihan soal, dan forum diskusi yang dapat membantu kamu belajar dengan lebih interaktif.
- Coursera: Platform pembelajaran online yang menawarkan berbagai kursus matematika, termasuk tentang bilangan pecahan berpangkat, dari universitas ternama di seluruh dunia. Beberapa kursus di Coursera berbayar, tetapi ada juga beberapa kursus yang ditawarkan secara gratis.
- edX: Platform pembelajaran online yang serupa dengan Coursera, menawarkan berbagai kursus matematika, termasuk tentang bilangan pecahan berpangkat, dari universitas ternama di seluruh dunia.
Artikel dan Jurnal Ilmiah
Artikel dan jurnal ilmiah dapat memberikan pemahaman yang lebih mendalam tentang bilangan pecahan berpangkat, termasuk sejarah, teori, dan aplikasi dalam berbagai bidang. Artikel dan jurnal ilmiah ini biasanya ditulis oleh para ahli matematika dan peneliti, sehingga memberikan informasi yang akurat dan terpercaya.
- Jurnal Matematika: Jurnal matematika seperti Jurnal Matematika Indonesia dan Jurnal Matematika Universitas Indonesia dapat menjadi sumber informasi yang baik untuk mempelajari tentang bilangan pecahan berpangkat.
- Artikel Ilmiah: Artikel ilmiah tentang bilangan pecahan berpangkat dapat ditemukan di berbagai platform seperti Google Scholar dan JSTOR.
Penutup
Mempelajari bilangan pecahan berpangkat tidak hanya membantu kita dalam menyelesaikan soal-soal matematika, tetapi juga membuka pemahaman kita tentang berbagai fenomena di sekitar kita. Dengan memahami konsep dan sifatnya, kita dapat menerapkannya dalam berbagai bidang, mulai dari perhitungan sederhana hingga analisis yang lebih kompleks.






