Contoh soal dan jawaban koordinat kartesius – Koordinat Kartesius, sistem yang menakjubkan yang menggabungkan garis bilangan horizontal dan vertikal untuk mendefinisikan lokasi titik pada bidang datar, memiliki peran penting dalam berbagai bidang, mulai dari matematika dan fisika hingga teknologi. Sistem ini memungkinkan kita untuk menggambarkan dan menganalisis posisi, gerakan, dan hubungan geometri secara tepat. Dalam artikel ini, kita akan menjelajahi dunia Koordinat Kartesius dengan mempelajari konsep dasarnya, memahami cara menentukan koordinat titik, menghitung jarak antar titik, dan bahkan mengungkap aplikasi menariknya dalam berbagai bidang.
Bersiaplah untuk merasakan bagaimana koordinat kartesius dapat membantu Anda memahami konsep geometri secara lebih mendalam. Mari kita selami dunia Koordinat Kartesius dan temukan bagaimana sistem ini dapat membantu Anda menyelesaikan berbagai masalah matematika, fisika, dan teknologi dengan lebih mudah!
Pengertian Koordinat Kartesius
Koordinat kartesius adalah sistem koordinat yang digunakan untuk menentukan posisi suatu titik dalam bidang datar atau ruang tiga dimensi. Sistem ini ditemukan oleh ahli matematika Prancis, René Descartes, pada abad ke-17.
Pengertian Koordinat Kartesius
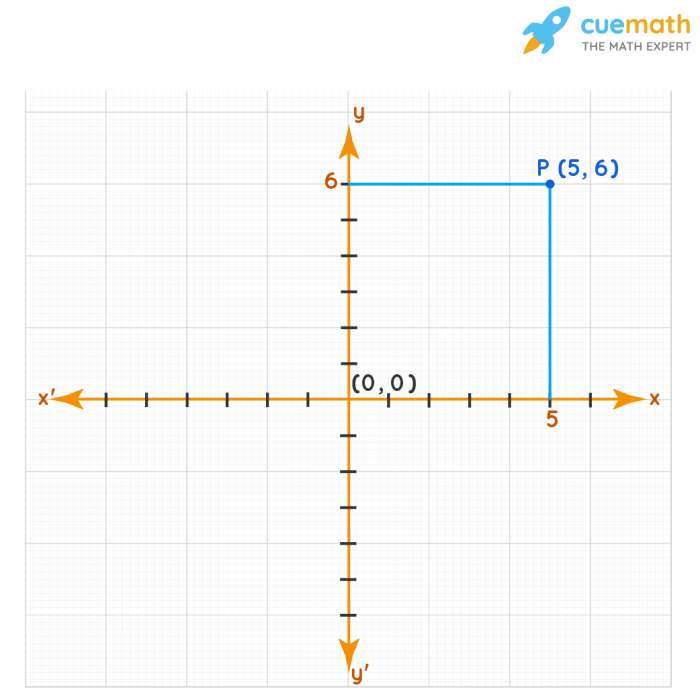
Koordinat kartesius merupakan sistem koordinat yang menggunakan dua garis lurus yang saling tegak lurus sebagai acuan. Garis-garis ini disebut sumbu x dan sumbu y. Titik potong kedua sumbu ini disebut titik asal (0, 0). Setiap titik dalam bidang dapat diwakili oleh pasangan terurut (x, y), di mana x adalah jarak titik tersebut dari sumbu y, dan y adalah jarak titik tersebut dari sumbu x.
Contoh Penggunaan Koordinat Kartesius dalam Kehidupan Sehari-hari
Koordinat kartesius memiliki banyak aplikasi dalam kehidupan sehari-hari. Berikut beberapa contohnya:
- Peta: Koordinat kartesius digunakan dalam peta untuk menentukan lokasi suatu tempat. Misalnya, koordinat (10, 5) dapat menunjukkan lokasi sebuah toko di peta.
- Navigasi GPS: Sistem GPS menggunakan koordinat kartesius untuk menentukan posisi suatu kendaraan atau perangkat. Koordinat GPS biasanya dinyatakan dalam bentuk derajat lintang dan bujur.
- Desain Grafis: Koordinat kartesius digunakan dalam desain grafis untuk menentukan posisi objek, seperti teks, gambar, dan bentuk, pada halaman atau layar.
- Permainan Video: Koordinat kartesius digunakan dalam permainan video untuk menentukan posisi karakter, objek, dan kamera dalam dunia virtual.
Hubungan Koordinat Kartesius dengan Arah Mata Angin
Koordinat kartesius dapat dihubungkan dengan arah mata angin. Sumbu x dapat dihubungkan dengan arah timur-barat, sedangkan sumbu y dapat dihubungkan dengan arah utara-selatan. Berikut tabel yang menunjukkan hubungan antara koordinat kartesius dengan arah mata angin:
| Koordinat Kartesius | Arah Mata Angin |
|---|---|
| (x, y) dengan x > 0 dan y > 0 | Timur Laut |
| (x, y) dengan x 0 | Utara Barat |
| (x, y) dengan x < 0 dan y < 0 | Barat Daya |
| (x, y) dengan x > 0 dan y < 0 | Selatan Timur |
Sumbu Koordinat
Sumbu koordinat merupakan bagian penting dalam sistem koordinat kartesius. Sumbu koordinat ini berperan sebagai garis acuan untuk menentukan posisi suatu titik dalam bidang datar. Dalam sistem koordinat kartesius, terdapat dua sumbu utama, yaitu sumbu x dan sumbu y. Kedua sumbu ini saling tegak lurus dan berpotongan di titik yang disebut titik asal (0, 0).
Fungsi Sumbu x dan Sumbu y
Sumbu x dan sumbu y memiliki fungsi yang berbeda dalam menentukan posisi suatu titik. Sumbu x, yang disebut juga sumbu horizontal, menunjukkan posisi titik secara horizontal atau kiri-kanan relatif terhadap titik asal. Sedangkan sumbu y, yang disebut juga sumbu vertikal, menunjukkan posisi titik secara vertikal atau atas-bawah relatif terhadap titik asal.
Contoh Koordinat Titik pada Sumbu x dan Sumbu y
- Titik (2, 0) terletak pada sumbu x karena nilai y-nya adalah 0. Titik ini berada 2 satuan ke kanan dari titik asal.
- Titik (0, 3) terletak pada sumbu y karena nilai x-nya adalah 0. Titik ini berada 3 satuan ke atas dari titik asal.
Ilustrasi Sumbu Koordinat
Bayangkan sebuah bidang datar dengan dua garis tegak lurus yang berpotongan di tengahnya. Garis horizontal adalah sumbu x dan garis vertikal adalah sumbu y. Titik potong kedua garis ini adalah titik asal (0, 0).
Misalkan kita ingin menggambarkan titik (3, 2). Untuk menemukan titik tersebut, kita bergerak 3 satuan ke kanan dari titik asal (sepanjang sumbu x) dan kemudian 2 satuan ke atas (sepanjang sumbu y). Titik yang kita temukan adalah titik (3, 2).
Menentukan Koordinat Titik
Pada bidang kartesius, setiap titik memiliki posisi unik yang didefinisikan oleh dua nilai: absis (nilai x) dan ordinat (nilai y). Menentukan koordinat titik adalah proses menemukan nilai absis dan ordinat yang tepat untuk titik tersebut.
Langkah-Langkah Menentukan Koordinat Titik
Berikut langkah-langkah untuk menentukan koordinat titik pada bidang kartesius:
- Identifikasi titik pada bidang kartesius: Tentukan titik yang ingin kamu cari koordinatnya. Titik ini bisa diwakili oleh simbol seperti titik atau lingkaran.
- Tarik garis tegak lurus dari titik ke sumbu x: Garis ini akan memotong sumbu x pada suatu titik. Titik potong ini menunjukkan nilai absis (nilai x) dari titik yang kamu cari.
- Tarik garis tegak lurus dari titik ke sumbu y: Garis ini akan memotong sumbu y pada suatu titik. Titik potong ini menunjukkan nilai ordinat (nilai y) dari titik yang kamu cari.
- Tuliskan koordinat titik: Koordinat titik ditulis dalam bentuk (x, y), dengan x mewakili nilai absis dan y mewakili nilai ordinat.
Contoh Penentuan Koordinat Titik
Misalnya, titik A terletak pada bidang kartesius. Untuk menentukan koordinat titik A, ikuti langkah-langkah berikut:
- Identifikasi titik A: Titik A diwakili oleh lingkaran kecil pada bidang kartesius.
- Tarik garis tegak lurus dari titik A ke sumbu x: Garis ini memotong sumbu x pada titik 3.
- Tarik garis tegak lurus dari titik A ke sumbu y: Garis ini memotong sumbu y pada titik 2.
- Tuliskan koordinat titik A: Koordinat titik A adalah (3, 2).
Diagram Aliran Menentukan Koordinat Titik
Berikut adalah diagram aliran yang menunjukkan langkah-langkah menentukan koordinat titik:
 |
Jarak Antar Titik: Contoh Soal Dan Jawaban Koordinat Kartesius
Pada bidang kartesius, setiap titik direpresentasikan dengan koordinat (x, y). Untuk mengetahui jarak antara dua titik, kita perlu menggunakan konsep Pythagoras. Jarak antara dua titik dapat dihitung dengan rumus yang didasarkan pada teorema Pythagoras.
Rumus Jarak Antar Titik
Rumus jarak antara dua titik A(x1, y1) dan B(x2, y2) pada bidang kartesius adalah:
AB = √[(x2 – x1)2 + (y2 – y1)2]
Rumus ini menyatakan bahwa jarak antara dua titik adalah akar kuadrat dari jumlah kuadrat selisih koordinat x dan koordinat y dari kedua titik tersebut.
Contoh Perhitungan Jarak
Misalnya, kita ingin menghitung jarak antara titik A(2, 3) dan B(5, 7). Berikut langkah-langkahnya:
- Tentukan koordinat x1, y1, x2, dan y2.
- Substitusikan nilai koordinat tersebut ke dalam rumus jarak.
- Hitung hasil dari rumus tersebut.
Dalam contoh ini, x1 = 2, y1 = 3, x2 = 5, dan y2 = 7. Maka, jarak antara titik A dan B adalah:
AB = √[(5 – 2)2 + (7 – 3)2] = √[32 + 42] = √(9 + 16) = √25 = 5
Jadi, jarak antara titik A(2, 3) dan B(5, 7) adalah 5 satuan.
Contoh soal dan jawaban koordinat kartesius memang menarik, tapi kalau kamu ingin tantangan yang lebih menantang, coba deh pelajari contoh soal metode saldo menurun ganda. Contoh soal metode saldo menurun ganda ini akan menguji kemampuanmu dalam menghitung depresiasi aset secara lebih cepat.
Setelah memahami metode ini, kamu bisa kembali ke contoh soal dan jawaban koordinat kartesius dengan lebih percaya diri!
Tabel Jarak Antar Titik
Berikut adalah tabel yang menunjukkan jarak antar titik dengan koordinat yang berbeda:
| Titik A | Titik B | Jarak AB |
|---|---|---|
| (1, 2) | (4, 6) | 5 |
| (-2, 1) | (3, -2) | √41 |
| (0, 0) | (5, 12) | 13 |
Titik Tengah Segmen Garis
Pada bidang kartesius, titik tengah segmen garis adalah titik yang membagi segmen garis menjadi dua bagian yang sama panjang. Pengetahuan tentang titik tengah segmen garis bermanfaat dalam berbagai aplikasi, seperti geometri, kalkulus, dan ilmu komputer.
Rumus Titik Tengah
Rumus titik tengah segmen garis menghubungkan dua titik dengan koordinat (x1, y1) dan (x2, y2) adalah:
Titik Tengah = ((x1 + x2) / 2, (y1 + y2) / 2)
Rumus ini menghitung rata-rata koordinat x dan koordinat y dari kedua titik ujung segmen garis.
Contoh Perhitungan Titik Tengah
Misalnya, kita ingin menentukan titik tengah segmen garis yang menghubungkan titik A (2, 3) dan titik B (6, 7).
- x1 = 2, y1 = 3
- x2 = 6, y2 = 7
Maka, titik tengah segmen garis AB adalah:
((2 + 6) / 2, (3 + 7) / 2) = (4, 5)
Diagram Titik Tengah
Diagram berikut menunjukkan titik tengah segmen garis AB yang telah kita hitung sebelumnya:
- Titik A (2, 3) diplot pada sumbu x dan sumbu y.
- Titik B (6, 7) diplot pada sumbu x dan sumbu y.
- Titik tengah segmen garis AB, yaitu (4, 5), diplot pada sumbu x dan sumbu y.
| Sumbu x | Sumbu y |
| 2 | 3 |
| 6 | 7 |
| 4 | 5 |
Diagram ini menunjukkan bahwa titik tengah segmen garis membagi segmen garis menjadi dua bagian yang sama panjang.
Aplikasi Koordinat Kartesius
Koordinat Kartesius, yang diciptakan oleh René Descartes, adalah sistem yang digunakan untuk menentukan lokasi suatu titik dalam ruang dua dimensi atau tiga dimensi. Sistem ini terdiri dari dua atau tiga sumbu tegak lurus yang saling berpotongan di titik asal. Sumbu-sumbu ini umumnya diberi label x, y, dan z. Koordinat Kartesius memiliki aplikasi luas dalam berbagai bidang, seperti matematika, fisika, dan teknologi.
Aplikasi Koordinat Kartesius dalam Matematika
Dalam matematika, koordinat Kartesius digunakan untuk menggambarkan dan menganalisis berbagai konsep geometri, seperti:
- Grafik Fungsi: Koordinat Kartesius memungkinkan kita untuk memvisualisasikan fungsi matematika dengan memplot titik-titik yang mewakili pasangan nilai input dan output. Misalnya, grafik fungsi y = x^2 akan menunjukkan kurva parabola yang melalui titik-titik (0, 0), (1, 1), (-1, 1), dan seterusnya.
- Geometri Analitik: Koordinat Kartesius digunakan untuk mempelajari bentuk geometri seperti garis, lingkaran, dan elips dengan menggunakan persamaan matematika. Misalnya, persamaan x^2 + y^2 = 1 mewakili lingkaran dengan jari-jari 1 dan pusat di titik asal.
- Vektor: Koordinat Kartesius digunakan untuk mewakili vektor, yang merupakan besaran yang memiliki besar dan arah. Vektor dapat direpresentasikan sebagai pasangan terurut (x, y) dalam ruang dua dimensi atau (x, y, z) dalam ruang tiga dimensi.
Aplikasi Koordinat Kartesius dalam Fisika, Contoh soal dan jawaban koordinat kartesius
Koordinat Kartesius memainkan peran penting dalam fisika untuk menggambarkan dan menganalisis gerak, gaya, dan medan.
- Kinematika: Koordinat Kartesius digunakan untuk menentukan posisi, kecepatan, dan percepatan suatu benda dalam ruang. Misalnya, posisi suatu benda pada waktu tertentu dapat dinyatakan sebagai (x, y, z) dalam koordinat Kartesius.
- Dinamika: Koordinat Kartesius digunakan untuk menganalisis gaya yang bekerja pada benda, seperti gaya gravitasi, gaya gesekan, dan gaya normal. Misalnya, gaya gravitasi pada benda dapat dinyatakan sebagai vektor (0, -mg) dalam koordinat Kartesius, di mana m adalah massa benda dan g adalah percepatan gravitasi.
- Elektromagnetisme: Koordinat Kartesius digunakan untuk menggambarkan medan elektromagnetik, yang merupakan gabungan dari medan listrik dan medan magnet. Misalnya, medan listrik yang dihasilkan oleh muatan titik dapat dinyatakan sebagai vektor (Ex, Ey, Ez) dalam koordinat Kartesius.
Aplikasi Koordinat Kartesius dalam Teknologi
Koordinat Kartesius digunakan dalam berbagai aplikasi teknologi, termasuk:
- Sistem Navigasi: Koordinat Kartesius digunakan dalam sistem navigasi GPS untuk menentukan lokasi perangkat pada permukaan bumi. Sistem ini menggunakan koordinat geografis (lintang dan bujur) yang kemudian diubah menjadi koordinat Kartesius untuk menentukan posisi perangkat.
- Pembuatan Peta dan Grafik: Koordinat Kartesius digunakan dalam pembuatan peta dan grafik untuk menampilkan data spasial. Misalnya, peta jalan menggunakan koordinat Kartesius untuk menunjukkan lokasi jalan, bangunan, dan tempat-tempat menarik lainnya.
- Komputer Grafis: Koordinat Kartesius digunakan dalam komputer grafis untuk menentukan posisi dan dimensi objek dalam ruang tiga dimensi. Sistem ini memungkinkan kita untuk membuat dan memanipulasi gambar dan model 3D secara virtual.
Tabel Aplikasi Koordinat Kartesius
| Bidang | Aplikasi |
|---|---|
| Matematika | Grafik Fungsi, Geometri Analitik, Vektor |
| Fisika | Kinematika, Dinamika, Elektromagnetisme |
| Teknologi | Sistem Navigasi, Pembuatan Peta dan Grafik, Komputer Grafis |
Soal dan Jawaban Koordinat Kartesius
Koordinat kartesius adalah sistem koordinat yang digunakan untuk menentukan posisi suatu titik dalam bidang dua dimensi atau ruang tiga dimensi. Sistem ini menggunakan dua garis tegak lurus, yaitu sumbu x dan sumbu y, yang saling berpotongan di titik asal (0, 0). Koordinat kartesius sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik, untuk menggambarkan dan menganalisis objek dan gerakan.
Pada artikel ini, kita akan membahas beberapa soal latihan tentang koordinat kartesius dan memberikan jawaban lengkap serta penjelasannya. Soal-soal ini akan meliputi berbagai konsep penting yang terkait dengan koordinat kartesius, seperti menentukan koordinat titik, jarak antara dua titik, dan persamaan garis.
Soal dan Jawaban Koordinat Kartesius
Berikut adalah 5 soal latihan tentang koordinat kartesius yang meliputi berbagai konsep, beserta jawaban lengkap dan penjelasannya.
| No | Soal | Jawaban | Penjelasan |
|---|---|---|---|
| 1 | Tentukan koordinat titik A yang terletak 3 satuan ke kanan dan 2 satuan ke atas dari titik asal (0, 0)! | (3, 2) | Karena titik A terletak 3 satuan ke kanan dari titik asal, maka nilai x-nya adalah 3. Karena titik A terletak 2 satuan ke atas dari titik asal, maka nilai y-nya adalah 2. Jadi, koordinat titik A adalah (3, 2). |
| 2 | Tentukan jarak antara titik P(2, 1) dan Q(5, 4)! | √18 atau 3√2 | Jarak antara dua titik dapat dihitung dengan menggunakan rumus jarak: √[(x2 – x1)2 + (y2 – y1)2]. Dalam hal ini, x1 = 2, y1 = 1, x2 = 5, dan y2 = 4. Substitusikan nilai-nilai ini ke dalam rumus jarak: √[(5 – 2)2 + (4 – 1)2] = √[32 + 32] = √(9 + 9) = √18 = 3√2. Jadi, jarak antara titik P dan Q adalah √18 atau 3√2. |
| 3 | Tentukan persamaan garis yang melalui titik (1, 2) dan (3, 6)! | y = 2x | Persamaan garis dapat ditentukan dengan menggunakan rumus: y – y1 = m(x – x1), di mana m adalah gradien garis. Gradien garis dapat dihitung dengan menggunakan rumus: m = (y2 – y1) / (x2 – x1). Dalam hal ini, x1 = 1, y1 = 2, x2 = 3, dan y2 = 6. Substitusikan nilai-nilai ini ke dalam rumus gradien: m = (6 – 2) / (3 – 1) = 4 / 2 = 2. Kemudian, substitusikan nilai m dan koordinat titik (1, 2) ke dalam rumus persamaan garis: y – 2 = 2(x – 1). Sederhanakan persamaan tersebut: y – 2 = 2x – 2. Jadi, persamaan garis yang melalui titik (1, 2) dan (3, 6) adalah y = 2x. |
| 4 | Tentukan koordinat titik tengah segmen garis yang menghubungkan titik A(-2, 3) dan B(4, 1)! | (1, 2) | Koordinat titik tengah segmen garis dapat dihitung dengan menggunakan rumus: [(x1 + x2) / 2, (y1 + y2) / 2]. Dalam hal ini, x1 = -2, y1 = 3, x2 = 4, dan y2 = 1. Substitusikan nilai-nilai ini ke dalam rumus titik tengah: [(-2 + 4) / 2, (3 + 1) / 2] = (2 / 2, 4 / 2) = (1, 2). Jadi, koordinat titik tengah segmen garis AB adalah (1, 2). |
| 5 | Tentukan persamaan lingkaran yang berpusat di titik (2, -1) dan memiliki jari-jari 3 satuan! | (x – 2)2 + (y + 1)2 = 9 | Persamaan lingkaran dengan pusat (h, k) dan jari-jari r adalah (x – h)2 + (y – k)2 = r2. Dalam hal ini, h = 2, k = -1, dan r = 3. Substitusikan nilai-nilai ini ke dalam rumus persamaan lingkaran: (x – 2)2 + (y – (-1))2 = 32. Sederhanakan persamaan tersebut: (x – 2)2 + (y + 1)2 = 9. Jadi, persamaan lingkaran yang berpusat di titik (2, -1) dan memiliki jari-jari 3 satuan adalah (x – 2)2 + (y + 1)2 = 9. |
Kesimpulan Akhir
Dengan memahami konsep koordinat kartesius, kita membuka pintu menuju pemahaman yang lebih dalam tentang geometri dan berbagai aplikasi menariknya dalam berbagai bidang. Dari menentukan lokasi objek pada peta hingga mengoptimalkan algoritma dalam teknologi, koordinat kartesius berperan penting dalam dunia modern. Semoga pemahaman yang kita dapatkan dari artikel ini dapat membantu Anda menjelajahi dunia matematika, fisika, dan teknologi dengan lebih percaya diri.