Logaritma, sebuah konsep matematika yang mungkin terdengar asing bagi sebagian orang, ternyata memiliki peran penting dalam berbagai bidang, mulai dari ilmu pengetahuan hingga teknologi. Konsep logaritma sendiri sebenarnya merupakan kebalikan dari eksponen, di mana logaritma menjawab pertanyaan “Berapakah pangkat yang harus diberikan pada suatu bilangan pokok agar menghasilkan suatu bilangan tertentu?”. Contoh Soal dan Jawaban Logaritma akan membantu Anda memahami konsep ini dengan lebih baik dan melihat bagaimana logaritma diterapkan dalam kehidupan sehari-hari.
Dalam artikel ini, kita akan menjelajahi dunia logaritma mulai dari pengertian dasar, sifat-sifatnya, hingga penerapannya dalam berbagai bidang. Kita akan membahas berbagai jenis logaritma, bagaimana menyelesaikan persamaan logaritma, dan tentu saja, dilengkapi dengan contoh soal dan jawaban yang menarik untuk memperkuat pemahaman Anda.
Jenis-Jenis Logaritma
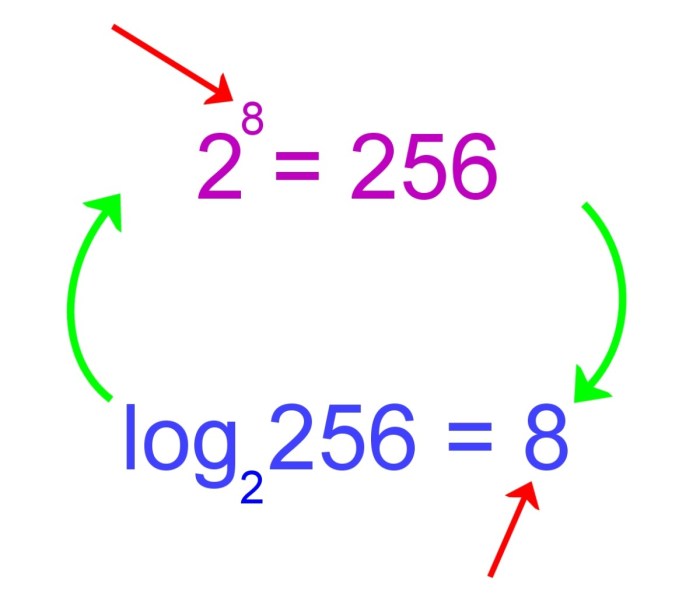
Logaritma merupakan fungsi invers dari eksponen. Dalam logaritma, kita mencari pangkat yang diperlukan untuk memperoleh suatu bilangan tertentu dengan basis tertentu. Jenis logaritma yang paling umum dipelajari adalah logaritma natural dan logaritma basis 10.
Logaritma Natural
Logaritma natural adalah logaritma dengan basis *e* (konstanta matematika yang nilainya sekitar 2,71828). Logaritma natural dinotasikan dengan ln(x).
Contoh: ln(e) = 1 karena *e* pangkat 1 sama dengan *e*.
Logaritma Basis 10
Logaritma basis 10 adalah logaritma dengan basis 10. Logaritma basis 10 dinotasikan dengan log(x).
Contoh: log(100) = 2 karena 10 pangkat 2 sama dengan 100.
Perbedaan Logaritma Natural dan Logaritma Basis 10
Perbedaan utama antara logaritma natural dan logaritma basis 10 adalah basisnya. Logaritma natural menggunakan basis *e*, sedangkan logaritma basis 10 menggunakan basis 10.
Perbedaan ini penting karena logaritma natural dan logaritma basis 10 memiliki aplikasi yang berbeda. Logaritma natural sering digunakan dalam matematika, fisika, dan ilmu komputer, sedangkan logaritma basis 10 lebih sering digunakan dalam kimia dan biologi.
Contoh Soal dan Jawaban
| Jenis Logaritma | Soal | Jawaban |
|---|---|---|
| Logaritma Natural | ln(e2) = ? | 2 |
| Logaritma Basis 10 | log(1000) = ? | 3 |
| Logaritma Natural | ln(1) = ? | 0 |
| Logaritma Basis 10 | log(1) = ? | 0 |
Penerapan Logaritma dalam Matematika: Contoh Soal Dan Jawaban Logaritma
Logaritma merupakan fungsi invers dari eksponen, yang memiliki peran penting dalam berbagai bidang matematika, termasuk kalkulus dan trigonometri. Penggunaan logaritma dalam kalkulus dan trigonometri memungkinkan kita untuk menyelesaikan masalah yang rumit dengan lebih mudah dan efisien.
Penerapan Logaritma dalam Kalkulus
Logaritma memainkan peran penting dalam kalkulus, khususnya dalam diferensial dan integral. Berikut adalah beberapa contoh penerapan logaritma dalam kalkulus:
- Diferensial: Turunan dari fungsi logaritma adalah 1/x, yang digunakan dalam menyelesaikan masalah yang melibatkan laju perubahan dan gradien. Misalnya, untuk menentukan laju perubahan populasi yang tumbuh secara eksponensial, kita dapat menggunakan turunan dari fungsi logaritma.
- Integral: Integral dari fungsi logaritma digunakan untuk menghitung luas daerah di bawah kurva dan volume benda putar. Misalnya, untuk menghitung volume benda putar yang dihasilkan dari rotasi kurva y = ln(x) di sekitar sumbu x, kita dapat menggunakan integral dari fungsi logaritma.
- Persamaan Diferensial: Logaritma digunakan untuk menyelesaikan persamaan diferensial, yang menggambarkan hubungan antara fungsi dan turunannya. Misalnya, dalam model pertumbuhan populasi, persamaan diferensial yang melibatkan fungsi eksponensial dapat diselesaikan menggunakan logaritma.
Penerapan Logaritma dalam Trigonometri
Logaritma juga dapat digunakan untuk menyelesaikan masalah dalam trigonometri, khususnya dalam hubungan antara sudut dan sisi segitiga. Berikut adalah contoh soal dan jawaban yang menunjukkan penerapan logaritma dalam trigonometri:
Soal:
Sebuah segitiga siku-siku memiliki sudut 30 derajat dan sisi miring 10 cm. Tentukan panjang sisi yang berhadapan dengan sudut 30 derajat.
Jawaban:
Diketahui:
– Sudut = 30 derajat
– Sisi miring = 10 cm
Rumus trigonometri yang berlaku:
sin(sudut) = sisi berhadapan / sisi miring
Maka:
sin(30 derajat) = sisi berhadapan / 10 cm
sisi berhadapan = sin(30 derajat) * 10 cm
sisi berhadapan = 0.5 * 10 cm
sisi berhadapan = 5 cm
Jadi, panjang sisi yang berhadapan dengan sudut 30 derajat adalah 5 cm.
Aplikasi Logaritma dalam Berbagai Bidang Matematika
Berikut adalah tabel yang menunjukkan aplikasi logaritma dalam berbagai bidang matematika:
| Bidang Matematika | Aplikasi Logaritma |
|---|---|
| Kalkulus | Diferensial, integral, persamaan diferensial |
| Trigonometri | Menentukan hubungan antara sudut dan sisi segitiga |
| Aljabar | Menyelesaikan persamaan eksponensial, memecahkan persamaan logaritma |
| Geometri | Menghitung luas dan volume bentuk geometris |
| Statistika | Menentukan skala logaritma untuk data yang tersebar luas |
Penerapan Logaritma dalam Kehidupan Sehari-hari
Logaritma, meskipun mungkin terlihat rumit, memiliki aplikasi yang luas dan penting dalam berbagai bidang kehidupan. Dari ilmu pengetahuan dan teknologi hingga ekonomi, logaritma membantu kita memahami dan mengukur berbagai fenomena dengan lebih mudah. Mari kita telusuri beberapa contoh konkret penerapan logaritma dalam kehidupan sehari-hari.
Skala Gempa Bumi, Contoh soal dan jawaban logaritma
Salah satu contoh paling terkenal dari penggunaan logaritma adalah dalam pengukuran skala gempa bumi. Skala Richter, yang digunakan untuk mengukur kekuatan gempa bumi, menggunakan logaritma basis 10. Setiap peningkatan satu satuan pada skala Richter menunjukkan peningkatan sepuluh kali lipat dalam amplitudo gelombang gempa.
Lagi bingung dengan contoh soal dan jawaban logaritma? Tenang, kamu bisa latihan dengan berbagai macam soal, mulai dari menentukan nilai logaritma hingga menyelesaikan persamaan logaritma. Ingat, memahami konsep dasar logaritma sangat penting. Misalnya, dalam menentukan titik sampel, kamu harus bisa menentukan semua kemungkinan hasil dari suatu kejadian.
Untuk lebih jelasnya, kamu bisa cek contoh soal titik sampel di sini. Dengan latihan yang cukup, kamu akan lebih mahir dalam menyelesaikan soal logaritma dan menguasai konsep dasar yang dibutuhkan.
Misalnya, gempa bumi dengan kekuatan 6 pada skala Richter memiliki amplitudo gelombang sepuluh kali lebih besar daripada gempa bumi dengan kekuatan 5.
Dengan menggunakan logaritma, skala Richter memungkinkan kita untuk menggambarkan intensitas gempa bumi yang sangat beragam, dari gempa bumi kecil yang hampir tidak terasa hingga gempa bumi besar yang menghancurkan.
Aplikasi Logaritma dalam Bidang Lainnya
Selain skala gempa bumi, logaritma memiliki banyak aplikasi lain dalam berbagai bidang, seperti:
- Ilmu Pengetahuan: Logaritma digunakan dalam kimia untuk menghitung pH suatu larutan, yang menunjukkan tingkat keasaman atau kebasaan. Logaritma juga digunakan dalam fisika untuk mempelajari peluruhan radioaktif.
- Teknologi: Logaritma digunakan dalam bidang komputer untuk mengukur kompresi data dan dalam pemrosesan sinyal untuk menganalisis frekuensi suara.
- Ekonomi: Logaritma digunakan untuk menghitung pertumbuhan ekonomi, tingkat inflasi, dan untuk menganalisis data keuangan.
- Musik: Logaritma digunakan dalam teori musik untuk memahami interval dan akord.
Tabel Aplikasi Logaritma
| Bidang | Aplikasi | Contoh |
|---|---|---|
| Ilmu Pengetahuan | Pengukuran pH, Peluruhan radioaktif | pH larutan asam, peluruhan karbon-14 |
| Teknologi | Kompresi data, Pemrosesan sinyal | Kompresi file audio, Analisis spektrum suara |
| Ekonomi | Pertumbuhan ekonomi, Tingkat inflasi | Pertumbuhan PDB, Inflasi tahunan |
| Musik | Interval dan akord | Oktaf, akord mayor dan minor |
Soal Latihan Logaritma
Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen. Dalam logaritma, kita mencari pangkat yang harus diterapkan pada suatu bilangan pokok untuk mendapatkan bilangan tertentu.
Untuk menguasai konsep logaritma, latihan soal sangat penting. Berikut adalah 5 soal latihan logaritma dengan tingkat kesulitan yang berbeda, lengkap dengan kunci jawabannya.
Soal Latihan Logaritma
Soal latihan logaritma berikut disusun untuk membantu kamu memahami konsep logaritma dan melatih kemampuan menyelesaikan soal logaritma.
| No | Soal | Kunci Jawaban |
|---|---|---|
| 1 | Tentukan nilai dari log2 8. | 3 |
| 2 | Tentukan nilai dari log3 27. | 3 |
| 3 | Tentukan nilai dari log5 125. | 3 |
| 4 | Selesaikan persamaan logaritma berikut: log2 (x + 1) = 3 | x = 7 |
| 5 | Tentukan nilai dari log4 64 + log2 8. | 6 |
Contoh Soal dan Jawaban Logaritma
Logaritma merupakan konsep matematika yang penting dalam berbagai bidang, seperti ilmu komputer, fisika, dan keuangan. Pengertian logaritma adalah invers dari eksponen, di mana logaritma suatu bilangan terhadap basis tertentu menyatakan pangkat yang harus diberikan pada basis tersebut untuk menghasilkan bilangan tersebut.
Konsep Dasar Logaritma
Berikut ini beberapa contoh soal dan jawaban yang membahas konsep dasar logaritma:
-
Soal: Tentukan nilai dari log2 8.
Jawaban: log2 8 = 3, karena 23 = 8. -
Soal: Hitung nilai dari log5 125.
Jawaban: log5 125 = 3, karena 53 = 125. -
Soal: Sederhanakan persamaan logaritma berikut: log3 27 + log3 9.
Jawaban: log3 27 + log3 9 = log3 (27 x 9) = log3 243 = 5.
Tips dan Trik Mempelajari Logaritma
Logaritma merupakan konsep matematika yang penting dalam berbagai bidang, seperti fisika, kimia, ekonomi, dan teknik. Namun, bagi sebagian orang, mempelajari logaritma bisa terasa menantang. Artikel ini akan membahas beberapa tips dan trik yang dapat membantu kamu memahami dan menguasai konsep logaritma dengan lebih mudah.
Memahami Konsep Dasar Logaritma
Langkah pertama dalam mempelajari logaritma adalah memahami konsep dasarnya. Logaritma adalah kebalikan dari eksponen. Jika kita memiliki persamaan eksponen a^b = c, maka logaritma dari c dengan basis a adalah b, ditulis sebagai log_a c = b.
- Pahami definisi logaritma dan hubungannya dengan eksponen.
- Pelajari sifat-sifat logaritma, seperti sifat perkalian, pembagian, dan pangkat.
- Latihlah dengan berbagai contoh soal untuk menguji pemahaman kamu tentang konsep dasar logaritma.
Membuat Peta Konsep
Membuat peta konsep dapat membantu kamu memahami hubungan antar konsep dalam logaritma. Peta konsep dapat menunjukkan hubungan antara logaritma dengan eksponen, sifat-sifat logaritma, dan berbagai jenis soal logaritma.
Latihan Soal
Latihan soal merupakan bagian penting dalam mempelajari logaritma. Dengan mengerjakan soal, kamu dapat menguji pemahaman dan kemampuan kamu dalam menerapkan konsep logaritma.
- Mulailah dengan soal-soal dasar dan tingkatkan kesulitannya secara bertahap.
- Kerjakan soal dengan berbagai variasi, seperti soal cerita, soal hitungan, dan soal penerapan.
- Jika kamu kesulitan dalam mengerjakan soal, jangan langsung menyerah. Cobalah untuk memahami konsep yang terkait dengan soal tersebut dan carilah bantuan dari guru atau teman.
Sumber Belajar
Terdapat berbagai sumber belajar yang dapat membantu kamu dalam mempelajari logaritma.
- Buku teks matematika: Pilih buku teks yang sesuai dengan level pendidikan kamu dan memiliki penjelasan yang mudah dipahami.
- Website edukasi: Ada banyak website edukasi yang menyediakan materi dan latihan soal logaritma secara gratis, seperti Khan Academy dan Mathplanet.
- Video tutorial: Video tutorial dapat membantu kamu dalam memahami konsep logaritma secara visual dan interaktif.
Menerapkan Logaritma dalam Kehidupan Sehari-hari
Logaritma memiliki banyak aplikasi dalam kehidupan sehari-hari.
- Dalam dunia komputer, logaritma digunakan dalam algoritma pengurutan dan pencarian.
- Dalam bidang keuangan, logaritma digunakan untuk menghitung bunga majemuk dan pertumbuhan investasi.
- Dalam ilmu pengetahuan, logaritma digunakan untuk mengukur skala gempa bumi, keasaman, dan intensitas suara.
Simpulan Akhir
Dengan memahami konsep logaritma, Anda akan membuka pintu menuju pemahaman yang lebih dalam tentang berbagai bidang ilmu pengetahuan dan teknologi. Contoh soal dan jawaban yang telah dibahas di sini memberikan gambaran nyata bagaimana logaritma bekerja dan bagaimana konsep ini diterapkan dalam berbagai situasi. Jangan ragu untuk terus belajar dan mengeksplorasi lebih jauh tentang logaritma. Anda akan menemukan bahwa konsep ini tidak hanya menarik, tetapi juga sangat bermanfaat dalam kehidupan sehari-hari.





