Contoh soal fungsi naik dan fungsi turun trigonometri – Pernahkah kamu memperhatikan bagaimana grafik fungsi trigonometri seperti sinus dan cosinus bergerak naik turun? Nah, itulah yang kita sebut dengan fungsi naik dan fungsi turun. Dalam artikel ini, kita akan menjelajahi lebih dalam tentang konsep ini, mulai dari pengertian hingga penerapannya dalam berbagai bidang.
Fungsi naik dan fungsi turun dalam trigonometri sangat penting dalam memahami pola pergerakan grafik fungsi trigonometri. Dengan memahami konsep ini, kita dapat menentukan interval di mana grafik fungsi naik atau turun, serta memprediksi perilaku grafik di masa depan. Selain itu, konsep ini juga memiliki aplikasi yang luas dalam berbagai bidang seperti fisika, teknik, dan ekonomi.
Pengertian Fungsi Naik dan Fungsi Turun Trigonometri
Fungsi trigonometri, seperti sinus, cosinus, dan tangen, merupakan fungsi periodik yang menggambarkan hubungan antara sudut dan sisi-sisi segitiga siku-siku. Fungsi-fungsi ini memiliki sifat khusus yang membedakannya, yaitu sifat naik dan turun. Fungsi naik menunjukkan bahwa nilai fungsi meningkat seiring dengan peningkatan nilai sudut, sedangkan fungsi turun menunjukkan bahwa nilai fungsi menurun seiring dengan peningkatan nilai sudut.
Pengertian Fungsi Naik dan Fungsi Turun Trigonometri
Secara formal, fungsi trigonometri dikatakan naik pada interval tertentu jika nilai fungsi meningkat seiring dengan peningkatan nilai sudut pada interval tersebut. Sebaliknya, fungsi trigonometri dikatakan turun pada interval tertentu jika nilai fungsi menurun seiring dengan peningkatan nilai sudut pada interval tersebut.
Ilustrasi Grafik Fungsi Naik dan Fungsi Turun Trigonometri
Berikut adalah ilustrasi grafik fungsi sinus (sin x) dan cosinus (cos x) untuk menunjukkan fungsi naik dan fungsi turun:
- Fungsi Sinus (sin x):
- Pada interval 0° hingga 90°, nilai fungsi sinus meningkat seiring dengan peningkatan nilai sudut. Ini berarti fungsi sinus naik pada interval ini.
- Pada interval 90° hingga 180°, nilai fungsi sinus menurun seiring dengan peningkatan nilai sudut. Ini berarti fungsi sinus turun pada interval ini.
- Fungsi Cosinus (cos x):
- Pada interval 0° hingga 90°, nilai fungsi cosinus menurun seiring dengan peningkatan nilai sudut. Ini berarti fungsi cosinus turun pada interval ini.
- Pada interval 90° hingga 180°, nilai fungsi cosinus meningkat seiring dengan peningkatan nilai sudut. Ini berarti fungsi cosinus naik pada interval ini.
Dengan demikian, kita dapat melihat bahwa fungsi trigonometri naik dan turun pada interval-interval tertentu. Ini penting untuk dipahami karena dapat membantu kita dalam menganalisis dan memahami perilaku fungsi trigonometri pada berbagai situasi.
Rumus Umum untuk Menentukan Interval Fungsi Naik dan Fungsi Turun Trigonometri
Untuk menentukan interval fungsi naik dan fungsi turun trigonometri, kita dapat menggunakan turunan pertama fungsi tersebut. Jika turunan pertama positif, maka fungsi tersebut naik. Jika turunan pertama negatif, maka fungsi tersebut turun. Berikut adalah rumus umum untuk menentukan interval fungsi naik dan fungsi turun trigonometri:
f'(x) > 0 => Fungsi naik
f'(x) Fungsi turun
Contohnya, untuk menentukan interval fungsi naik dan fungsi turun fungsi sinus (sin x), kita dapat menggunakan turunan pertama fungsi sinus, yaitu cos x. Jika cos x > 0, maka fungsi sinus naik. Jika cos x < 0, maka fungsi sinus turun. Dengan demikian, kita dapat menentukan interval fungsi naik dan fungsi turun fungsi sinus dengan menggunakan turunan pertama fungsi tersebut.
Menentukan Interval Fungsi Naik dan Fungsi Turun
Dalam matematika, khususnya dalam kalkulus, memahami sifat fungsi sangatlah penting. Salah satu sifat penting yang perlu kita pahami adalah apakah fungsi tersebut naik atau turun pada interval tertentu. Untuk fungsi trigonometri, menentukan interval fungsi naik dan fungsi turun membutuhkan pemahaman tentang turunan dan periodisitas fungsi trigonometri.
Menentukan Interval Fungsi Naik dan Fungsi Turun
Untuk menentukan interval fungsi naik dan fungsi turun suatu fungsi trigonometri, kita perlu melakukan langkah-langkah berikut:
- Tentukan turunan pertama fungsi trigonometri tersebut.
- Cari titik-titik stasioner, yaitu titik-titik di mana turunan pertama sama dengan nol atau tidak terdefinisi.
- Buat tabel yang menunjukkan tanda turunan pertama pada setiap interval yang dibentuk oleh titik-titik stasioner.
- Jika turunan pertama positif pada suatu interval, maka fungsi tersebut naik pada interval tersebut. Sebaliknya, jika turunan pertama negatif pada suatu interval, maka fungsi tersebut turun pada interval tersebut.
Contoh Soal Fungsi Trigonometri
Sebagai contoh, mari kita tentukan interval fungsi naik dan fungsi turun dari fungsi y = sin(x) pada interval 0 ≤ x ≤ 2π.
Contoh soal fungsi naik dan fungsi turun trigonometri bisa jadi rumit, tapi dengan latihan yang cukup, kamu pasti bisa menguasainya. Nah, untuk memahami konsep yang lebih luas, kamu bisa cek contoh soal kasus persalinan beserta jawabannya yang bisa memberikan perspektif baru tentang penerapan matematika dalam kehidupan nyata.
Dengan memahami berbagai kasus, kamu akan lebih siap dalam menghadapi soal-soal fungsi naik dan fungsi turun trigonometri yang mungkin muncul di ujian!
- Turunan pertama dari y = sin(x) adalah y’ = cos(x).
- Titik-titik stasioner adalah titik-titik di mana cos(x) = 0, yaitu x = π/2 dan x = 3π/2.
- Kita dapat membuat tabel berikut untuk menunjukkan tanda turunan pertama pada setiap interval:
| Interval | 0 ≤ x < π/2 | π/2 < x < 3π/2 | 3π/2 < x ≤ 2π |
|---|---|---|---|
| Tanda y’ | + | – | + |
| Sifat Fungsi | Naik | Turun | Naik |
Berdasarkan tabel di atas, kita dapat menyimpulkan bahwa fungsi y = sin(x) naik pada interval 0 ≤ x < π/2 dan 3π/2 < x ≤ 2π, dan turun pada interval π/2 < x < 3π/2.
Tabel Interval Fungsi Naik dan Fungsi Turun
Berikut adalah tabel yang menunjukkan interval fungsi naik dan fungsi turun untuk berbagai jenis fungsi trigonometri:
| Fungsi | Interval Fungsi Naik | Interval Fungsi Turun |
|---|---|---|
| y = sin(x) | 2nπ ≤ x ≤ (2n + 1)π | (2n + 1)π ≤ x ≤ (2n + 2)π |
| y = cos(x) | (2n – 1)π ≤ x ≤ 2nπ | 2nπ ≤ x ≤ (2n + 1)π |
| y = tan(x) | (2n – 1)π/2 < x < (2n + 1)π/2 | Tidak ada |
| y = cot(x) | Tidak ada | (2n – 1)π/2 < x < (2n + 1)π/2 |
| y = sec(x) | (2n – 1)π ≤ x ≤ 2nπ | 2nπ ≤ x ≤ (2n + 1)π |
| y = csc(x) | 2nπ ≤ x ≤ (2n + 1)π | (2n + 1)π ≤ x ≤ (2n + 2)π |
Keterangan: n adalah bilangan bulat.
Penerapan Fungsi Naik dan Fungsi Turun dalam Konteks Nyata
Fungsi naik dan fungsi turun trigonometri tidak hanya berperan penting dalam matematika, tetapi juga memiliki aplikasi yang luas dalam berbagai bidang seperti fisika, teknik, dan ekonomi. Penerapannya memungkinkan kita untuk menganalisis dan memprediksi perilaku sistem yang dinamis dan periodik.
Aplikasi dalam Fisika
Fungsi trigonometri, khususnya fungsi sinus dan kosinus, memiliki peran penting dalam memahami dan memprediksi gerakan periodik, seperti gerakan osilasi dan gelombang. Sebagai contoh, fungsi sinus digunakan untuk memodelkan gerakan harmonik sederhana, seperti gerakan bandul atau pegas.
- Gerakan harmonik sederhana: Fungsi sinus digunakan untuk menggambarkan posisi, kecepatan, dan percepatan suatu objek yang bergerak secara periodik.
- Gelombang: Fungsi sinus dan kosinus digunakan untuk menggambarkan bentuk gelombang, seperti gelombang suara dan gelombang elektromagnetik.
Aplikasi dalam Teknik
Fungsi trigonometri memiliki aplikasi yang luas dalam berbagai bidang teknik, termasuk desain mesin, konstruksi, dan elektronik. Fungsi trigonometri membantu dalam menganalisis dan mendesain sistem yang melibatkan gerakan periodik dan sudut.
- Desain mesin: Fungsi trigonometri digunakan untuk menganalisis gerakan piston dalam mesin, menentukan torsi dan daya yang dihasilkan, dan mendesain sistem transmisi.
- Konstruksi: Fungsi trigonometri digunakan untuk menghitung sudut dan panjang dalam desain struktur, seperti jembatan, gedung, dan menara.
- Elektronik: Fungsi trigonometri digunakan untuk menganalisis sinyal periodik dalam sirkuit elektronik, seperti sinyal AC dan gelombang radio.
Aplikasi dalam Ekonomi
Fungsi trigonometri juga memiliki aplikasi dalam ekonomi, terutama dalam analisis data musiman dan siklus bisnis. Fungsi trigonometri membantu dalam mengidentifikasi pola periodik dalam data ekonomi dan memprediksi tren di masa depan.
- Analisis data musiman: Fungsi trigonometri digunakan untuk mengidentifikasi pola periodik dalam data ekonomi, seperti penjualan ritel atau produksi industri, yang dipengaruhi oleh musim.
- Siklus bisnis: Fungsi trigonometri digunakan untuk menganalisis siklus bisnis, seperti ekspansi dan resesi, yang memiliki sifat periodik.
Soal Latihan Fungsi Naik dan Fungsi Turun Trigonometri
Setelah memahami konsep fungsi naik dan fungsi turun pada trigonometri, mari kita uji pemahamanmu dengan beberapa soal latihan. Soal-soal berikut ini dirancang dengan tingkat kesulitan yang berbeda, mulai dari yang mudah hingga yang menantang. Dengan mengerjakan soal-soal ini, kamu akan semakin mahir dalam menentukan interval fungsi naik dan fungsi turun trigonometri.
Soal Latihan dan Pembahasan
Berikut ini 5 soal latihan fungsi naik dan fungsi turun trigonometri beserta pembahasannya:
- Tentukan interval fungsi naik dan fungsi turun dari fungsi $y = sin(x)$ pada interval $0 \leq x \leq 2\pi$.
- Tentukan interval fungsi naik dan fungsi turun dari fungsi $y = cos(2x)$ pada interval $0 \leq x \leq \pi$.
- Tentukan interval fungsi naik dan fungsi turun dari fungsi $y = tan(x)$ pada interval $-\frac\pi2 < x < \frac\pi2$.
- Tentukan interval fungsi naik dan fungsi turun dari fungsi $y = cot(x)$ pada interval $0 < x < \pi$.
- Tentukan interval fungsi naik dan fungsi turun dari fungsi $y = sec(x)$ pada interval $0 \leq x \leq 2\pi$.
Pembahasan Soal Latihan
Berikut pembahasan untuk setiap soal latihan yang telah diberikan:
Soal 1
Fungsi $y = sin(x)$ naik pada interval $0 \leq x \leq \frac\pi2$ dan $\frac3\pi2 \leq x \leq 2\pi$, dan turun pada interval $\frac\pi2 \leq x \leq \frac3\pi2$. Hal ini dapat dilihat dari grafik fungsi sinus, yang berbentuk gelombang. Pada interval $0 \leq x \leq \frac\pi2$, grafik fungsi sinus naik, sedangkan pada interval $\frac\pi2 \leq x \leq \frac3\pi2$, grafik fungsi sinus turun, dan seterusnya.
Soal 2
Fungsi $y = cos(2x)$ naik pada interval $0 \leq x \leq \frac\pi4$ dan $\frac3\pi4 \leq x \leq \pi$, dan turun pada interval $\frac\pi4 \leq x \leq \frac3\pi4$. Hal ini dapat dilihat dari grafik fungsi cosinus, yang juga berbentuk gelombang. Namun, karena fungsi ini adalah $cos(2x)$, periodenya menjadi setengah dari periode fungsi $cos(x)$, yaitu $\pi$. Pada interval $0 \leq x \leq \frac\pi4$, grafik fungsi cosinus naik, sedangkan pada interval $\frac\pi4 \leq x \leq \frac3\pi4$, grafik fungsi cosinus turun, dan seterusnya.
Soal 3
Fungsi $y = tan(x)$ naik pada interval $-\frac\pi2 < x < \frac\pi2$. Hal ini dapat dilihat dari grafik fungsi tangen, yang berbentuk asimtotik. Grafik fungsi tangen selalu naik pada interval $-\frac\pi2 < x < \frac\pi2$.
Soal 4
Fungsi $y = cot(x)$ turun pada interval $0 < x < \pi$. Hal ini dapat dilihat dari grafik fungsi cotangen, yang juga berbentuk asimtotik. Grafik fungsi cotangen selalu turun pada interval $0 < x < \pi$.
Soal 5
Fungsi $y = sec(x)$ naik pada interval $0 \leq x < \frac\pi2$ dan $\pi \leq x < \frac3\pi2$, dan turun pada interval $\frac\pi2 < x \leq \pi$ dan $\frac3\pi2 < x \leq 2\pi$. Hal ini dapat dilihat dari grafik fungsi secan, yang berbentuk asimtotik. Grafik fungsi secan naik pada interval $0 \leq x < \frac\pi2$ dan $\pi \leq x < \frac3\pi2$, dan turun pada interval $\frac\pi2 < x \leq \pi$ dan $\frac3\pi2 < x \leq 2\pi$.
Hubungan Fungsi Naik dan Fungsi Turun dengan Turunan
Dalam dunia matematika, turunan fungsi trigonometri memegang peranan penting dalam menentukan perilaku fungsi, khususnya dalam mengidentifikasi interval di mana fungsi tersebut naik atau turun. Hubungan antara turunan dan fungsi naik-turun ini didasarkan pada konsep bahwa turunan positif menunjukkan fungsi naik, sedangkan turunan negatif menunjukkan fungsi turun.
Menentukan Interval Fungsi Naik dan Fungsi Turun
Untuk menentukan interval fungsi naik dan fungsi turun dari suatu fungsi trigonometri, kita perlu mengikuti langkah-langkah berikut:
- Tentukan turunan pertama fungsi trigonometri tersebut.
- Cari nilai-nilai kritis, yaitu nilai-nilai x yang membuat turunan pertama sama dengan nol atau tidak terdefinisi.
- Buat tabel tanda turunan pertama dengan menguji nilai x di setiap interval yang dibentuk oleh nilai-nilai kritis.
- Jika turunan pertama positif pada suatu interval, maka fungsi naik pada interval tersebut. Sebaliknya, jika turunan pertama negatif pada suatu interval, maka fungsi turun pada interval tersebut.
Contoh Fungsi Trigonometri
Misalnya, kita ingin menentukan interval fungsi naik dan fungsi turun dari fungsi trigonometri f(x) = sin(x) pada interval 0 ≤ x ≤ 2π.
- Turunan pertama dari f(x) = sin(x) adalah f'(x) = cos(x).
- Nilai kritis dari f'(x) = cos(x) adalah x = π/2 dan x = 3π/2, karena cos(π/2) = 0 dan cos(3π/2) = 0.
- Tabel tanda turunan pertama:
Interval 0 ≤ x < π/2 π/2 < x < 3π/2 3π/2 < x ≤ 2π Tanda f'(x) + – + Perilaku f(x) Naik Turun Naik
Berdasarkan tabel di atas, fungsi f(x) = sin(x) naik pada interval 0 ≤ x < π/2 dan 3π/2 < x ≤ 2π, dan turun pada interval π/2 < x < 3π/2.
Contoh Penerapan Fungsi Naik dan Fungsi Turun dalam Graf
Memahami fungsi naik dan fungsi turun pada graf fungsi trigonometri sangat penting untuk menganalisis perilaku dan karakteristik fungsi tersebut. Dengan mengamati graf, kita dapat menentukan interval di mana fungsi tersebut meningkat atau menurun, memberikan wawasan tentang bagaimana nilai fungsi berubah seiring perubahan nilai input.
Menganalisis Graf Fungsi Trigonometri
Graf fungsi trigonometri, seperti sinus dan cosinus, memiliki pola berulang yang khas. Untuk menentukan interval fungsi naik dan fungsi turun, kita perlu memperhatikan titik-titik puncak dan lembah pada graf. Titik puncak menunjukkan titik di mana fungsi mencapai nilai maksimum, sementara titik lembah menunjukkan titik di mana fungsi mencapai nilai minimum.
- Fungsi Naik: Interval di mana graf fungsi bergerak naik dari kiri ke kanan, menunjukkan bahwa nilai fungsi meningkat seiring peningkatan nilai input.
- Fungsi Turun: Interval di mana graf fungsi bergerak turun dari kiri ke kanan, menunjukkan bahwa nilai fungsi menurun seiring peningkatan nilai input.
Contoh Soal
Perhatikan graf fungsi y = sin(x) di bawah ini. Graf ini menunjukkan satu siklus lengkap fungsi sinus dari 0 hingga 2π.
|
|
Berdasarkan graf tersebut, kita dapat menentukan interval fungsi naik dan fungsi turun sebagai berikut:
- Fungsi Naik: Interval fungsi naik berada di antara 0 dan π/2, serta antara 3π/2 dan 2π. Dalam interval ini, graf fungsi bergerak naik dari kiri ke kanan.
- Fungsi Turun: Interval fungsi turun berada di antara π/2 dan 3π/2. Dalam interval ini, graf fungsi bergerak turun dari kiri ke kanan.
Contoh lain, perhatikan graf fungsi y = cos(x) di bawah ini. Graf ini menunjukkan satu siklus lengkap fungsi cosinus dari 0 hingga 2π.
|
|
Berdasarkan graf tersebut, kita dapat menentukan interval fungsi naik dan fungsi turun sebagai berikut:
- Fungsi Naik: Interval fungsi naik berada di antara π dan 2π. Dalam interval ini, graf fungsi bergerak naik dari kiri ke kanan.
- Fungsi Turun: Interval fungsi turun berada di antara 0 dan π. Dalam interval ini, graf fungsi bergerak turun dari kiri ke kanan.
Dengan memahami bagaimana menganalisis graf fungsi trigonometri, kita dapat dengan mudah menentukan interval fungsi naik dan fungsi turun, yang memberikan wawasan tentang perilaku dan karakteristik fungsi tersebut.
Kegunaan Fungsi Naik dan Fungsi Turun Trigonometri
Fungsi naik dan fungsi turun dalam trigonometri merupakan konsep penting yang memiliki aplikasi luas dalam berbagai bidang. Pemahaman tentang bagaimana fungsi trigonometri berubah seiring dengan perubahan sudut sangat krusial dalam memecahkan masalah di matematika, fisika, teknik, dan ilmu lainnya. Mari kita telusuri lebih dalam tentang kegunaan fungsi naik dan fungsi turun trigonometri.
Aplikasi Fungsi Naik dan Fungsi Turun dalam Matematika
Dalam matematika, fungsi naik dan fungsi turun trigonometri digunakan untuk menganalisis perilaku fungsi trigonometri dan memahami sifat-sifatnya. Misalnya, dalam menentukan interval di mana fungsi sinus naik atau turun, kita dapat mengetahui kapan fungsi tersebut mencapai nilai maksimum atau minimum. Informasi ini sangat berguna dalam menentukan solusi persamaan trigonometri, menggambar grafik fungsi trigonometri, dan memahami konsep-konsep matematika yang lebih kompleks seperti turunan dan integral.
Aplikasi Fungsi Naik dan Fungsi Turun dalam Fisika
Fungsi naik dan fungsi turun trigonometri memiliki peran penting dalam fisika, terutama dalam bidang mekanika, gelombang, dan listrik. Contohnya, dalam gerak harmonik sederhana, fungsi sinus dan kosinus digunakan untuk menggambarkan posisi, kecepatan, dan percepatan benda yang bergerak bolak-balik.
- Dalam gelombang, fungsi trigonometri digunakan untuk menggambarkan bentuk gelombang, amplitudo, dan frekuensi.
- Dalam listrik, fungsi trigonometri digunakan untuk menggambarkan tegangan dan arus bolak-balik.
Aplikasi Fungsi Naik dan Fungsi Turun dalam Teknik, Contoh soal fungsi naik dan fungsi turun trigonometri
Fungsi naik dan fungsi turun trigonometri sangat berguna dalam berbagai bidang teknik, seperti teknik sipil, teknik mesin, dan teknik elektro. Dalam teknik sipil, fungsi trigonometri digunakan untuk menghitung sudut kemiringan, tinggi bangunan, dan jarak antar titik.
- Dalam teknik mesin, fungsi trigonometri digunakan untuk menghitung gaya, momen, dan torsi yang bekerja pada benda.
- Dalam teknik elektro, fungsi trigonometri digunakan untuk menghitung tegangan, arus, dan daya dalam rangkaian AC.
Aplikasi Fungsi Naik dan Fungsi Turun dalam Ilmu Lainnya
Fungsi naik dan fungsi turun trigonometri juga memiliki aplikasi yang luas dalam ilmu lainnya, seperti astronomi, meteorologi, dan geologi. Dalam astronomi, fungsi trigonometri digunakan untuk menghitung posisi bintang dan planet. Dalam meteorologi, fungsi trigonometri digunakan untuk memprediksi cuaca dan memahami pola angin. Dalam geologi, fungsi trigonometri digunakan untuk mempelajari struktur batuan dan tanah.
Contoh Kasus Nyata
Sebagai contoh, dalam desain jembatan, fungsi trigonometri digunakan untuk menghitung gaya yang bekerja pada struktur jembatan akibat beban kendaraan dan angin. Dengan mengetahui fungsi naik dan turun trigonometri, para insinyur dapat merancang jembatan yang kuat dan aman. Contoh lain, dalam bidang navigasi, fungsi trigonometri digunakan untuk menentukan posisi kapal atau pesawat terbang. Dengan mengetahui sudut dan jarak, navigasi dapat dilakukan dengan lebih akurat.
Kontribusi Fungsi Naik dan Fungsi Turun dalam Pengembangan Ilmu Pengetahuan dan Teknologi
Fungsi naik dan fungsi turun trigonometri telah memberikan kontribusi yang besar dalam pengembangan ilmu pengetahuan dan teknologi. Pemahaman tentang fungsi trigonometri telah memungkinkan para ilmuwan dan insinyur untuk memecahkan masalah yang kompleks dan mengembangkan teknologi baru. Sebagai contoh, pengembangan sistem GPS (Global Positioning System) tidak akan mungkin terjadi tanpa pemahaman tentang fungsi trigonometri. Sistem GPS menggunakan fungsi trigonometri untuk menentukan posisi objek di bumi dengan sangat akurat.
Contoh Soal Penerapan Fungsi Naik dan Fungsi Turun
Fungsi naik dan fungsi turun dalam trigonometri memiliki aplikasi yang luas dalam kehidupan sehari-hari. Untuk memahami konsep ini dengan lebih baik, mari kita lihat contoh soal cerita yang melibatkan penerapan fungsi naik dan fungsi turun trigonometri dalam kehidupan sehari-hari.
Contoh Soal Cerita
Seorang petani ingin menanam pohon pisang di lahannya. Ia ingin memastikan bahwa pohon pisang tersebut terkena sinar matahari yang cukup sepanjang hari. Lahannya memiliki bentuk persegi panjang dengan panjang 10 meter dan lebar 5 meter. Ia ingin menanam pohon pisang di sepanjang sisi panjang lahannya, dengan jarak antar pohon pisang 2 meter. Pohon pisang memiliki tinggi 3 meter dan lebar 1 meter. Petani tersebut ingin mengetahui berapa sudut elevasi matahari yang dibutuhkan agar pohon pisang tersebut terkena sinar matahari secara maksimal pada pukul 12 siang.
Langkah-langkah Penyelesaian
- Langkah pertama adalah menentukan posisi matahari pada pukul 12 siang. Pada pukul 12 siang, matahari berada di titik tertinggi di langit, sehingga sudut elevasi matahari mencapai nilai maksimum.
- Selanjutnya, kita perlu menentukan sudut elevasi matahari yang dibutuhkan agar sinar matahari mengenai puncak pohon pisang. Karena pohon pisang memiliki tinggi 3 meter, maka sudut elevasi matahari haruslah lebih besar dari sudut elevasi yang terbentuk antara puncak pohon pisang dengan titik di tanah yang berjarak 2 meter dari pohon pisang.
- Untuk menentukan sudut elevasi tersebut, kita dapat menggunakan fungsi tangen. Tangen sudut elevasi sama dengan perbandingan tinggi pohon pisang dengan jarak antara pohon pisang dan titik di tanah.
- Dengan menggunakan kalkulator atau tabel trigonometri, kita dapat menghitung sudut elevasi yang dibutuhkan. Dalam kasus ini, sudut elevasi yang dibutuhkan adalah sekitar 56,3 derajat.
Penjelasan
Fungsi naik dan fungsi turun dalam trigonometri sangat membantu dalam memahami dan menganalisis fenomena nyata, seperti dalam contoh soal cerita di atas. Fungsi naik dan fungsi turun trigonometri memungkinkan kita untuk menghitung sudut elevasi matahari yang dibutuhkan agar pohon pisang terkena sinar matahari secara maksimal. Dengan memahami konsep fungsi naik dan fungsi turun trigonometri, kita dapat mengaplikasikannya dalam berbagai bidang, seperti arsitektur, teknik sipil, dan navigasi.
Strategi Mempelajari Fungsi Naik dan Fungsi Turun Trigonometri: Contoh Soal Fungsi Naik Dan Fungsi Turun Trigonometri
Mempelajari fungsi naik dan fungsi turun trigonometri mungkin terlihat rumit, namun dengan strategi yang tepat, kamu bisa menaklukkannya dengan mudah. Ada beberapa tips dan trik yang bisa kamu terapkan untuk memahami konsep ini dengan lebih baik.
Memahami Konsep Dasar
Sebelum mempelajari fungsi naik dan turun trigonometri, pastikan kamu memahami konsep dasar trigonometri seperti:
- Sudut dan ukurannya dalam derajat dan radian
- Nilai sinus, cosinus, dan tangen untuk sudut-sudut istimewa
- Grafik fungsi sinus, cosinus, dan tangen
Mempelajari Fungsi Naik dan Turun
Setelah memahami konsep dasar, kamu bisa mulai mempelajari fungsi naik dan turun trigonometri. Berikut beberapa strategi yang bisa kamu gunakan:
- Pelajari definisi fungsi naik dan turun. Fungsi naik berarti nilai fungsi meningkat seiring dengan peningkatan nilai variabel independen, sedangkan fungsi turun berarti nilai fungsi menurun seiring dengan peningkatan nilai variabel independen.
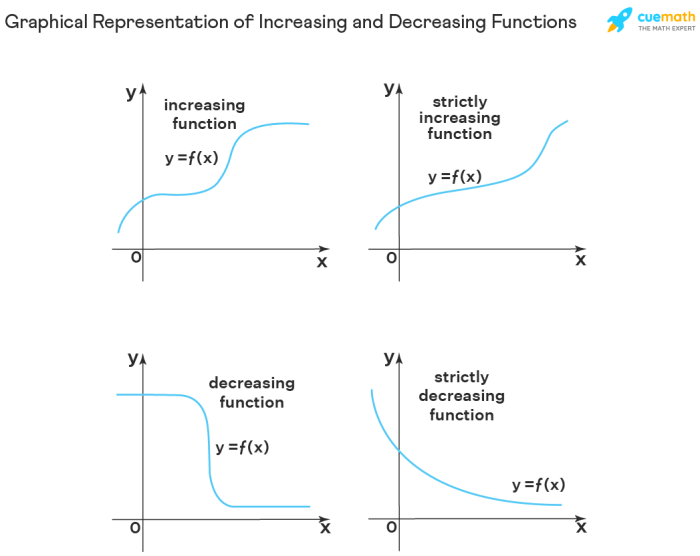
- Perhatikan grafik fungsi. Grafik fungsi sinus, cosinus, dan tangen dapat membantu kamu memahami kapan fungsi naik dan kapan fungsi turun. Misalnya, fungsi sinus naik pada interval 0 hingga π/2 dan 3π/2 hingga 2π, dan turun pada interval π/2 hingga 3π/2.
- Gunakan turunan. Turunan fungsi trigonometri dapat digunakan untuk menentukan kapan fungsi naik dan kapan fungsi turun. Jika turunan fungsi positif, maka fungsi naik, dan jika turunan fungsi negatif, maka fungsi turun.
- Latih dengan contoh soal. Latihan soal dengan berbagai macam variasi dapat membantu kamu memahami konsep fungsi naik dan turun trigonometri dengan lebih baik.
Sumber Belajar
Ada banyak sumber belajar yang bisa kamu gunakan untuk mempelajari fungsi naik dan turun trigonometri. Berikut beberapa sumber yang relevan dan terpercaya:
- Buku teks matematika. Buku teks matematika tingkat SMA atau perguruan tinggi biasanya memuat materi tentang fungsi naik dan turun trigonometri.
- Website edukasi. Banyak website edukasi yang menyediakan materi pembelajaran tentang trigonometri, termasuk fungsi naik dan turun. Beberapa contohnya adalah Khan Academy, Coursera, dan edX.
- Video tutorial. YouTube merupakan sumber video tutorial yang baik untuk mempelajari fungsi naik dan turun trigonometri. Banyak tutor matematika yang membuat video tutorial tentang topik ini.
- Aplikasi pembelajaran. Beberapa aplikasi pembelajaran seperti Photomath dan Wolfram Alpha dapat membantu kamu menyelesaikan soal-soal trigonometri, termasuk soal tentang fungsi naik dan turun.
Pentingnya Latihan dan Pemahaman Konsep
Latihan dan pemahaman konsep merupakan kunci untuk menguasai fungsi naik dan turun trigonometri. Berikut beberapa tips untuk mencapai hal tersebut:
- Kerjakan latihan soal secara rutin. Semakin banyak soal yang kamu kerjakan, semakin kuat pemahamanmu tentang konsep fungsi naik dan turun trigonometri.
- Mintalah bantuan guru atau tutor. Jika kamu mengalami kesulitan memahami konsep tertentu, jangan ragu untuk meminta bantuan guru atau tutor.
- Berdiskusi dengan teman sekelas. Berdiskusi dengan teman sekelas tentang konsep fungsi naik dan turun trigonometri dapat membantu kamu memahami konsep tersebut dari perspektif yang berbeda.
Pemungkas
Memahami fungsi naik dan fungsi turun trigonometri akan membuka pintu untuk memahami pola pergerakan grafik fungsi trigonometri dengan lebih mendalam. Dengan mempelajari konsep ini, kita dapat mengaplikasikannya dalam berbagai bidang, baik dalam menyelesaikan soal matematika maupun dalam memahami fenomena alam.




