Contoh soal garis berpotongan – Pernahkah kamu memperhatikan dua garis yang saling berpotongan pada peta? Atau mungkin melihat dua jalan yang saling berpotongan di kotamu? Nah, itulah contoh konkret dari konsep garis berpotongan dalam matematika. Garis berpotongan merupakan dua garis lurus yang memiliki satu titik persekutuan, atau dengan kata lain, titik di mana kedua garis tersebut saling bertemu.
Konsep garis berpotongan tidak hanya sebatas teori abstrak, tetapi juga memiliki aplikasi yang luas dalam kehidupan sehari-hari, seperti dalam bidang arsitektur, desain, dan bahkan dalam menentukan lokasi di peta. Pada artikel ini, kita akan menjelajahi lebih dalam tentang garis berpotongan, mulai dari pengertian, ciri-ciri, cara menentukan titik potong, hingga contoh soal dan penerapannya dalam berbagai bidang.
Konsep Sudut pada Garis Berpotongan
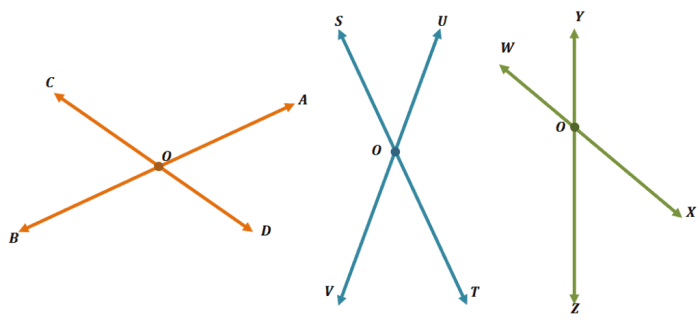
Ketika dua garis bertemu atau berpotongan, mereka membentuk sudut-sudut yang memiliki sifat dan hubungan khusus. Pemahaman tentang jenis-jenis sudut ini penting dalam berbagai bidang, termasuk geometri, matematika, dan ilmu pengetahuan lainnya.
Contoh soal garis berpotongan biasanya melibatkan dua persamaan linear yang menggambarkan dua garis. Nah, untuk memahami lebih dalam tentang persamaan linear, kamu bisa cek contoh soal persamaan linier yang tersedia di sana. Setelah memahami persamaan linear, kamu akan lebih mudah menyelesaikan soal-soal garis berpotongan, karena pada dasarnya, kedua topik ini saling berkaitan.
Contohnya, menentukan titik potong dua garis bisa dilakukan dengan menyelesaikan sistem persamaan linear yang menggambarkan kedua garis tersebut.
Jenis-Jenis Sudut pada Garis Berpotongan, Contoh soal garis berpotongan
Ada beberapa jenis sudut yang terbentuk ketika dua garis berpotongan, yaitu:
- Sudut Berpelurus: Dua sudut yang berpelurus adalah sudut yang saling berdampingan dan jumlahnya 180 derajat.
- Sudut Berseberangan: Dua sudut yang berseberangan adalah sudut yang terletak di sisi berlawanan dari titik potong dua garis dan memiliki ukuran yang sama.
- Sudut Sehadap: Dua sudut yang sehadap adalah sudut yang terletak di sisi yang sama dari titik potong dua garis dan memiliki ukuran yang sama.
- Sudut Bersebelahan: Dua sudut yang bersebelahan adalah sudut yang terletak di sisi yang sama dari titik potong dua garis dan jumlahnya 180 derajat.
Contoh Ilustrasi Gambar
Berikut ini adalah contoh ilustrasi gambar yang menunjukkan berbagai jenis sudut pada garis berpotongan:
Misalnya, perhatikan dua garis lurus, garis A dan garis B, yang berpotongan di titik O. Pada titik potong ini, terbentuk empat sudut yang diberi label sebagai berikut: sudut 1, sudut 2, sudut 3, dan sudut 4.
Sudut 1 dan sudut 2 merupakan sudut berpelurus, karena keduanya saling berdampingan dan jumlahnya 180 derajat. Sudut 1 dan sudut 3 merupakan sudut berseberangan, karena keduanya terletak di sisi berlawanan dari titik potong dan memiliki ukuran yang sama. Sudut 1 dan sudut 4 merupakan sudut sehadap, karena keduanya terletak di sisi yang sama dari titik potong dan memiliki ukuran yang sama. Sudut 2 dan sudut 4 merupakan sudut bersebelahan, karena keduanya terletak di sisi yang sama dari titik potong dan jumlahnya 180 derajat.
Tabel Jenis Sudut
| Jenis Sudut | Definisi | Contoh Gambar |
|---|---|---|
| Sudut Berpelurus | Dua sudut yang saling berdampingan dan jumlahnya 180 derajat. | [Gambar ilustrasi sudut berpelurus] |
| Sudut Berseberangan | Dua sudut yang terletak di sisi berlawanan dari titik potong dua garis dan memiliki ukuran yang sama. | [Gambar ilustrasi sudut berseberangan] |
| Sudut Sehadap | Dua sudut yang terletak di sisi yang sama dari titik potong dua garis dan memiliki ukuran yang sama. | [Gambar ilustrasi sudut sehadap] |
| Sudut Bersebelahan | Dua sudut yang terletak di sisi yang sama dari titik potong dua garis dan jumlahnya 180 derajat. | [Gambar ilustrasi sudut bersebelahan] |
Contoh Soal Garis Berpotongan dalam Geometri Analitik
Garis berpotongan dalam geometri analitik merupakan konsep yang menarik karena melibatkan persamaan garis dan titik potongnya. Titik potong merupakan titik yang terletak pada kedua garis tersebut, dan bisa ditemukan dengan menyelesaikan sistem persamaan yang mewakili kedua garis tersebut. Berikut contoh soal yang bisa kita selesaikan bersama.
Menentukan Titik Potong Dua Garis
Misalkan kita memiliki dua garis dengan persamaan berikut:
* Garis 1: y = 2x + 1
* Garis 2: y = -x + 4
Titik potong kedua garis tersebut dapat ditentukan dengan mencari nilai x dan y yang memenuhi kedua persamaan. Ada beberapa cara untuk menentukan titik potong, salah satunya adalah dengan metode substitusi.
Metode Substitusi
Dalam metode substitusi, kita akan mengganti salah satu variabel dalam persamaan dengan nilai variabel tersebut dari persamaan lainnya.
Langkah-langkahnya:
- Dari persamaan Garis 1, kita tahu bahwa y = 2x + 1. Kita bisa substitusikan nilai y ini ke persamaan Garis 2.
- Substitusi y = 2x + 1 ke persamaan Garis 2: (2x + 1) = -x + 4.
- Selesaikan persamaan untuk mencari nilai x: 2x + x = 4 – 1, sehingga 3x = 3, dan x = 1.
- Substitusikan nilai x = 1 ke salah satu persamaan garis (misalnya, Garis 1) untuk mencari nilai y: y = 2(1) + 1, sehingga y = 3.
Jadi, titik potong kedua garis tersebut adalah (1, 3).
Ilustrasi
Untuk lebih memahami, kita bisa mengilustrasikan titik potong kedua garis tersebut dengan membuat grafik kedua garis.
Grafik Kedua Garis
Grafik kedua garis tersebut akan menunjukkan bahwa kedua garis tersebut berpotongan pada titik (1, 3).
Kesimpulan
Melalui contoh soal ini, kita dapat memahami bagaimana menentukan titik potong dua garis dalam geometri analitik. Metode substitusi merupakan salah satu metode yang bisa digunakan untuk menyelesaikan soal ini. Titik potong tersebut merupakan titik yang terletak pada kedua garis tersebut, dan dapat ditemukan dengan menyelesaikan sistem persamaan yang mewakili kedua garis.
Penutup: Contoh Soal Garis Berpotongan
Dengan memahami konsep garis berpotongan, kita dapat mengaplikasikannya dalam berbagai bidang, mulai dari menyelesaikan masalah matematika hingga memecahkan masalah nyata di kehidupan sehari-hari. Menentukan titik potong antara dua garis merupakan langkah penting dalam berbagai bidang seperti arsitektur, desain, dan navigasi. Semoga pembahasan ini bermanfaat untuk meningkatkan pemahamanmu tentang garis berpotongan.





