Contoh soal gradien garis – Pernahkah kamu bertanya-tanya bagaimana menentukan kemiringan suatu garis? Atau bagaimana menghubungkan persamaan garis dengan kemiringannya? Nah, konsep gradien garis hadir untuk menjawab pertanyaan-pertanyaan tersebut. Gradien garis adalah ukuran kemiringan suatu garis, yang menunjukkan seberapa curam atau landai garis tersebut. Dalam artikel ini, kita akan menjelajahi konsep gradien garis, mulai dari pengertian dasar hingga penerapannya dalam berbagai bidang, seperti matematika, ilmu pengetahuan, dan ekonomi.
Gradien garis memiliki peran penting dalam berbagai bidang, baik dalam matematika maupun ilmu pengetahuan. Dengan memahami konsep gradien, kita dapat menganalisis dan memahami hubungan antara dua variabel, seperti hubungan antara harga dan kuantitas barang dalam ilmu ekonomi, atau hubungan antara waktu dan jarak dalam ilmu fisika. Melalui contoh soal yang disertakan, kita akan belajar cara menghitung gradien garis, menentukan persamaan garis, dan mengaplikasikan konsep ini dalam berbagai situasi.
Pengertian Gradien Garis
Gradien garis adalah ukuran kemiringan atau kecondongan suatu garis. Dalam istilah yang lebih sederhana, gradien menunjukkan seberapa cepat garis naik atau turun saat bergerak ke kanan. Gradien garis memiliki peran penting dalam berbagai bidang, seperti geometri, kalkulus, dan fisika, karena dapat digunakan untuk menggambarkan hubungan antara variabel yang berbeda.
Contoh soal gradien garis biasanya melibatkan persamaan garis dan titik-titik yang diketahui. Nah, kalau kamu ingin mendalami konsep gradien lebih lanjut, kamu bisa coba pelajari contoh soal fungsi turunan. Contoh soal fungsi turunan akan membantumu memahami bagaimana gradien bisa dihubungkan dengan perubahan nilai fungsi pada suatu titik.
Setelah memahami konsep turunan, kamu bisa kembali ke contoh soal gradien garis dan menyelesaikannya dengan lebih mudah.
Ilustrasi Gradien Garis, Contoh soal gradien garis
Bayangkan sebuah jalan yang menanjak. Semakin curam jalan tersebut, semakin besar gradiennya. Begitu pula dengan garis, semakin curam garis tersebut, semakin besar gradiennya.
Misalnya, perhatikan garis lurus yang melewati titik (1, 2) dan (3, 4). Garis ini naik 2 satuan ke atas untuk setiap 2 satuan ke kanan. Oleh karena itu, gradien garis ini adalah 2/2 = 1.
Rumus Gradien Garis
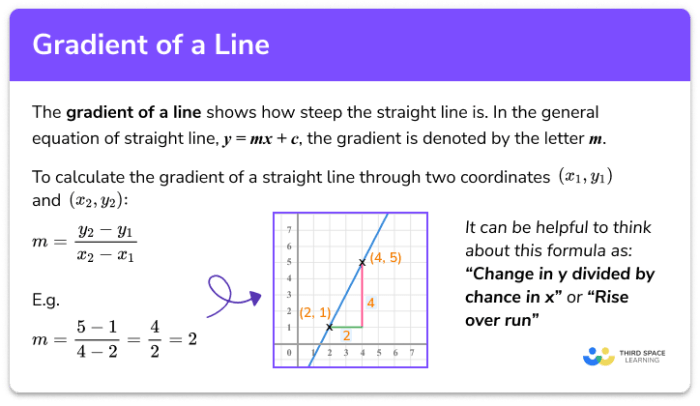
Gradien garis (m) dapat dihitung dengan menggunakan rumus:
m = (y2 – y1) / (x2 – x1)
Dimana (x1, y1) dan (x2, y2) adalah dua titik yang terletak pada garis tersebut.
Jenis-Jenis Gradien Garis
Terdapat beberapa jenis gradien garis, yang diklasifikasikan berdasarkan arah dan kemiringannya:
| Jenis Gradien | Contoh |
|---|---|
| Gradien Positif | Garis yang naik ke kanan. Contoh: Garis yang menghubungkan titik (1, 2) dan (3, 4). |
| Gradien Negatif | Garis yang turun ke kanan. Contoh: Garis yang menghubungkan titik (1, 4) dan (3, 2). |
| Gradien Nol | Garis horizontal. Contoh: Garis yang sejajar dengan sumbu x. |
| Gradien Tak Terdefinisi | Garis vertikal. Contoh: Garis yang sejajar dengan sumbu y. |
Cara Menghitung Gradien Garis
Gradien garis merupakan ukuran kemiringan atau kecondongan suatu garis. Gradien dapat positif, negatif, nol, atau tidak terdefinisi. Garis dengan gradien positif miring ke atas dari kiri ke kanan, sedangkan garis dengan gradien negatif miring ke bawah dari kiri ke kanan. Garis horizontal memiliki gradien nol, sedangkan garis vertikal memiliki gradien tidak terdefinisi.
Menghitung Gradien Garis dengan Dua Titik
Untuk menghitung gradien garis dengan menggunakan dua titik, kita dapat menggunakan rumus berikut:
m = (y2 – y1) / (x2 – x1)
Dimana:
- m adalah gradien garis
- (x1, y1) adalah koordinat titik pertama
- (x2, y2) adalah koordinat titik kedua
Berikut adalah langkah-langkah untuk menghitung gradien garis dengan menggunakan dua titik:
- Tentukan koordinat dua titik pada garis.
- Substitusikan nilai koordinat titik pertama dan kedua ke dalam rumus gradien.
- Hitung selisih ordinat (y2 – y1) dan selisih absis (x2 – x1).
- Bagi selisih ordinat dengan selisih absis untuk mendapatkan nilai gradien.
Contoh soal:
Tentukan gradien garis yang melalui titik A(2, 3) dan B(5, 9).
Penyelesaian:
- Titik A(2, 3) dan B(5, 9) adalah dua titik pada garis.
- Substitusikan nilai koordinat titik A dan B ke dalam rumus gradien:
- Hitung selisih ordinat (9 – 3) = 6 dan selisih absis (5 – 2) = 3.
- Bagi selisih ordinat dengan selisih absis: 6 / 3 = 2.
m = (9 – 3) / (5 – 2)
Jadi, gradien garis yang melalui titik A(2, 3) dan B(5, 9) adalah 2.
Menghitung Gradien Garis dari Persamaan Garis
Persamaan garis umumnya ditulis dalam bentuk y = mx + c, dimana m adalah gradien dan c adalah konstanta. Untuk menentukan gradien garis dari persamaan garis, kita hanya perlu melihat koefisien x.
Contoh soal:
Tentukan gradien garis yang memiliki persamaan y = 2x + 5.
Penyelesaian:
Koefisien x dalam persamaan garis y = 2x + 5 adalah 2. Jadi, gradien garis tersebut adalah 2.
Aplikasi Gradien Garis
Gradien garis merupakan konsep penting dalam matematika yang memiliki aplikasi luas dalam berbagai bidang kehidupan sehari-hari. Gradien garis menunjukkan kemiringan atau kecondongan suatu garis, yang dapat membantu kita memahami dan menganalisis berbagai fenomena, mulai dari kecepatan mobil hingga pertumbuhan ekonomi.
Aplikasi Gradien Garis dalam Kehidupan Sehari-hari
Gradien garis sering dijumpai dalam kehidupan sehari-hari, meskipun kita mungkin tidak menyadarinya. Beberapa contoh aplikasi gradien garis dalam kehidupan sehari-hari meliputi:
- Kecepatan Mobil: Gradien garis pada grafik kecepatan-waktu menunjukkan kecepatan mobil. Semakin besar gradien, semakin cepat mobil tersebut bergerak.
- Kemiringan Jalan: Gradien garis dapat digunakan untuk menentukan kemiringan jalan. Kemiringan yang lebih besar menunjukkan jalan yang lebih curam.
- Pertumbuhan Tanaman: Gradien garis pada grafik tinggi tanaman terhadap waktu menunjukkan laju pertumbuhan tanaman. Semakin besar gradien, semakin cepat tanaman tumbuh.
Aplikasi Gradien Garis dalam Matematika dan Ilmu Pengetahuan
Gradien garis memiliki peran penting dalam berbagai bidang matematika dan ilmu pengetahuan. Dalam kalkulus, gradien garis digunakan untuk menentukan turunan suatu fungsi. Turunan menunjukkan laju perubahan fungsi pada titik tertentu. Dalam fisika, gradien garis digunakan untuk menentukan kecepatan dan percepatan benda.
Aplikasi Gradien Garis dalam Bidang Ekonomi
Gradien garis dapat digunakan untuk menganalisis data ekonomi, seperti hubungan antara harga dan permintaan. Misalnya, jika kita membuat grafik hubungan antara harga dan permintaan suatu produk, gradien garis menunjukkan elastisitas permintaan. Elastisitas permintaan menunjukkan seberapa besar perubahan permintaan terhadap perubahan harga.
Contoh Soal:
Misalnya, sebuah perusahaan ingin mengetahui bagaimana perubahan harga suatu produk mempengaruhi permintaan. Perusahaan mengumpulkan data harga dan permintaan produk selama beberapa bulan terakhir dan membuat grafik hubungan antara keduanya. Grafik menunjukkan bahwa hubungan antara harga dan permintaan adalah linear.
Grafik menunjukkan bahwa ketika harga meningkat, permintaan menurun. Gradien garis menunjukkan elastisitas permintaan. Jika gradien garis negatif dan besar, maka permintaan elastis. Artinya, perubahan harga yang kecil akan menyebabkan perubahan permintaan yang besar. Jika gradien garis negatif dan kecil, maka permintaan tidak elastis. Artinya, perubahan harga yang besar hanya akan menyebabkan perubahan permintaan yang kecil.
Tabel Aplikasi Gradien Garis
Berikut adalah tabel yang berisi aplikasi gradien garis dalam berbagai bidang:
| Bidang | Aplikasi Gradien Garis |
|---|---|
| Matematika | Menentukan turunan fungsi, menganalisis fungsi linear |
| Fisika | Menentukan kecepatan dan percepatan benda, menganalisis gerak lurus |
| Ekonomi | Menganalisis hubungan antara harga dan permintaan, menghitung elastisitas permintaan |
| Teknik Sipil | Menentukan kemiringan jalan, mendesain struktur bangunan |
| Geografi | Menganalisis relief permukaan bumi, menentukan gradien sungai |
Contoh Soal Gradien Garis dengan Persamaan
Gradien garis merupakan nilai yang menunjukkan kemiringan atau kecondongan suatu garis. Gradien garis dapat ditentukan dengan berbagai cara, salah satunya dengan menggunakan persamaan garis. Persamaan garis sendiri memiliki beberapa bentuk, seperti persamaan garis dalam bentuk umum, bentuk slope-intercept, dan bentuk titik-lereng. Artikel ini akan membahas cara menentukan gradien garis dari persamaan garis, memberikan contoh soal, dan menjelaskan bagaimana menentukan persamaan garis jika gradien dan titik potongnya diketahui.
Menentukan Gradien Garis dari Persamaan Garis
Untuk menentukan gradien garis dari persamaan garis, kita dapat mengubah persamaan tersebut ke dalam bentuk slope-intercept, yaitu y = mx + c, dimana m adalah gradien dan c adalah titik potong sumbu y. Berikut adalah langkah-langkah yang dapat digunakan:
- Ubah persamaan garis ke dalam bentuk slope-intercept (y = mx + c).
- Identifikasi nilai m, yang merupakan koefisien dari x. Nilai m inilah yang merupakan gradien garis.
Contoh Soal Menentukan Gradien Garis dari Persamaan Garis
Misalnya, kita memiliki persamaan garis 2x + 3y = 6. Untuk menentukan gradien garis, kita perlu mengubah persamaan tersebut ke dalam bentuk slope-intercept. Berikut adalah langkah-langkahnya:
- Ubah persamaan garis menjadi 3y = -2x + 6.
- Bagi kedua ruas persamaan dengan 3, sehingga diperoleh y = (-2/3)x + 2.
- Dari persamaan tersebut, dapat diketahui bahwa gradien garis (m) adalah -2/3.
Tabel Contoh Soal Menentukan Gradien Garis dari Persamaan Garis
| Persamaan Garis | Bentuk Slope-Intercept | Gradien (m) |
|---|---|---|
| 2x + 3y = 6 | y = (-2/3)x + 2 | -2/3 |
| x – 2y = 4 | y = (1/2)x – 2 | 1/2 |
| y = 3x – 5 | y = 3x – 5 | 3 |
| y = -x + 1 | y = -x + 1 | -1 |
Menentukan Persamaan Garis jika Gradien dan Titik Potong Diketahui
Jika gradien (m) dan titik potong sumbu y (c) diketahui, maka persamaan garis dapat langsung ditentukan dengan menggunakan bentuk slope-intercept (y = mx + c).
Contohnya, jika gradien garis adalah 2 dan titik potong sumbu y adalah 3, maka persamaan garisnya adalah y = 2x + 3.
Gradien Garis Sejajar dan Tegak Lurus
Dalam mempelajari persamaan garis, kita sering kali menemukan konsep gradien. Gradien merupakan ukuran kemiringan suatu garis, yang menunjukkan seberapa cepat garis tersebut naik atau turun. Konsep gradien ini memiliki keterkaitan erat dengan garis sejajar dan tegak lurus. Mari kita bahas lebih lanjut mengenai hubungan antara gradien garis sejajar dan tegak lurus.
Hubungan Gradien Garis Sejajar dan Tegak Lurus
Gradien garis sejajar dan tegak lurus memiliki hubungan khusus. Garis sejajar memiliki gradien yang sama, sementara garis tegak lurus memiliki gradien yang saling berkebalikan dan negatif.
Contoh Soal Menentukan Gradien Garis Sejajar dan Tegak Lurus
Misalkan kita memiliki garis dengan persamaan y = 2x + 3. Kita ingin menentukan persamaan garis yang sejajar dan tegak lurus dengan garis tersebut, yang melewati titik (1, 4).
- Menentukan Gradien Garis Sejajar
Gradien garis sejajar sama dengan gradien garis awal, yaitu 2. Jadi, gradien garis sejajar adalah 2.
- Menentukan Persamaan Garis Sejajar
Kita dapat menggunakan rumus persamaan garis y – y1 = m(x – x1) dengan m = 2 dan titik (1, 4). Substitusikan nilai-nilai tersebut ke dalam rumus:
y – 4 = 2(x – 1)
Sederhanakan persamaan tersebut:
y – 4 = 2x – 2
y = 2x + 2
Jadi, persamaan garis yang sejajar dengan garis y = 2x + 3 dan melewati titik (1, 4) adalah y = 2x + 2.
- Menentukan Gradien Garis Tegak Lurus
Gradien garis tegak lurus merupakan kebalikan negatif dari gradien garis awal. Jadi, gradien garis tegak lurus adalah -1/2.
- Menentukan Persamaan Garis Tegak Lurus
Kita gunakan kembali rumus persamaan garis y – y1 = m(x – x1) dengan m = -1/2 dan titik (1, 4). Substitusikan nilai-nilai tersebut ke dalam rumus:
y – 4 = -1/2(x – 1)
Sederhanakan persamaan tersebut:
y – 4 = -1/2x + 1/2
y = -1/2x + 9/2
Jadi, persamaan garis yang tegak lurus dengan garis y = 2x + 3 dan melewati titik (1, 4) adalah y = -1/2x + 9/2.
Tabel Hubungan Gradien Garis Sejajar dan Tegak Lurus
| Jenis Garis | Hubungan Gradien |
|---|---|
| Sejajar | Gradien sama |
| Tegak Lurus | Gradien saling berkebalikan dan negatif |
Cara Menentukan Persamaan Garis Sejajar atau Tegak Lurus
Untuk menentukan persamaan garis yang sejajar atau tegak lurus dengan garis tertentu, kita perlu mengetahui gradien garis tersebut. Setelah itu, kita dapat menggunakan rumus persamaan garis y – y1 = m(x – x1) untuk menentukan persamaan garis yang sejajar atau tegak lurus, dengan m adalah gradien dan (x1, y1) adalah titik yang dilalui oleh garis tersebut.
Penerapan Gradien Garis dalam Bidang Teknik
Gradien garis merupakan konsep dasar dalam matematika yang memiliki aplikasi luas dalam berbagai bidang teknik. Gradien garis menunjukkan kemiringan atau kecondongan suatu garis, yang dapat digunakan untuk menentukan perubahan suatu variabel terhadap variabel lainnya. Dalam bidang teknik, gradien garis digunakan untuk menganalisis dan merancang berbagai sistem, seperti struktur, aliran fluida, dan sirkuit listrik.
Aplikasi Gradien Garis dalam Bidang Teknik
Berikut beberapa contoh aplikasi gradien garis dalam bidang teknik:
- Struktur: Gradien garis digunakan untuk menghitung kemiringan lereng dan menentukan stabilitas struktur, seperti jembatan dan gedung.
- Aliran Fluida: Gradien garis digunakan untuk menentukan kecepatan aliran fluida dalam pipa dan saluran, serta untuk menganalisis aliran fluida dalam sistem hidrolik.
- Sirkuit Listrik: Gradien garis digunakan untuk menghitung tegangan dan arus dalam sirkuit listrik, serta untuk menganalisis perilaku komponen elektronik.
- Mesin: Gradien garis digunakan untuk menganalisis kinerja mesin, seperti mesin pembakaran internal dan turbin, serta untuk menentukan efisiensi dan konsumsi bahan bakar.
Contoh Soal Aplikasi Gradien Garis dalam Bidang Teknik
Sebuah jalan tol memiliki kemiringan 5% (gradien 0,05). Jika jalan tol tersebut memiliki panjang 100 meter, berapa ketinggian perubahan jalan tol tersebut?
Penyelesaian:
Gradien garis didefinisikan sebagai perubahan ketinggian (Δy) dibagi dengan perubahan jarak horizontal (Δx). Dalam kasus ini, gradien garis = 0,05 dan Δx = 100 meter. Oleh karena itu, kita dapat menghitung Δy dengan rumus berikut:
gradien garis = Δy / Δx
0,05 = Δy / 100
Δy = 0,05 x 100 = 5 meter
Jadi, ketinggian perubahan jalan tol tersebut adalah 5 meter.
Tabel Aplikasi Gradien Garis dalam Berbagai Bidang Teknik
| Bidang Teknik | Aplikasi Gradien Garis |
|---|---|
| Struktur | Menghitung kemiringan lereng, menentukan stabilitas struktur, menganalisis beban dan tegangan |
| Aliran Fluida | Menganalisis aliran fluida dalam pipa dan saluran, menentukan kecepatan aliran, menganalisis tekanan |
| Sirkuit Listrik | Menganalisis tegangan dan arus dalam sirkuit listrik, menentukan resistansi, menganalisis perilaku komponen elektronik |
| Mesin | Menganalisis kinerja mesin, menentukan efisiensi, menghitung konsumsi bahan bakar, menganalisis gaya dan momen |
| Geoteknik | Menganalisis stabilitas lereng, menentukan kemiringan lereng, menganalisis aliran air tanah |
| Transportasi | Menganalisis kemiringan jalan, menentukan jarak tempuh, menganalisis kecepatan dan percepatan |
Menentukan Kemiringan Lereng dan Sudut Elevasi
Gradien garis dapat digunakan untuk menentukan kemiringan lereng dan sudut elevasi. Kemiringan lereng didefinisikan sebagai perubahan ketinggian dibagi dengan perubahan jarak horizontal. Sudut elevasi adalah sudut antara garis horizontal dan garis yang menghubungkan dua titik pada lereng.
Misalnya, jika gradien garis lereng adalah 0,25, maka kemiringan lereng adalah 25%. Sudut elevasi dapat dihitung dengan menggunakan fungsi trigonometri tangen (tan), yaitu tan(sudut elevasi) = gradien garis.
Ringkasan Penutup
Dengan memahami konsep gradien garis, kita dapat melihat dunia dengan perspektif yang lebih luas. Gradien garis tidak hanya membantu kita dalam memahami hubungan antara dua variabel, tetapi juga memungkinkan kita untuk memprediksi tren dan membuat keputusan yang lebih tepat. Mulai dari menentukan kemiringan jalan hingga menganalisis pertumbuhan ekonomi, gradien garis memiliki aplikasi yang luas dan penting dalam kehidupan sehari-hari.






