Contoh soal gradien garis lurus – Pernahkah Anda memperhatikan kemiringan jalan atau lereng bukit? Ternyata, kemiringan tersebut dapat diukur dengan konsep matematika yang disebut gradien garis lurus. Gradien garis lurus merupakan nilai yang menunjukkan seberapa curam atau landai suatu garis. Konsep ini sangat berguna dalam berbagai bidang, seperti konstruksi, ekonomi, dan ilmu pengetahuan.
Pada artikel ini, kita akan menjelajahi lebih dalam tentang gradien garis lurus. Mulai dari pengertian dasar, cara menghitung gradien, hingga penerapannya dalam kehidupan sehari-hari. Siapkan diri Anda untuk mempelajari konsep menarik ini dan siap-siap mengasah kemampuan menyelesaikan soal-soal gradien garis lurus!
Pengertian Gradien Garis Lurus: Contoh Soal Gradien Garis Lurus
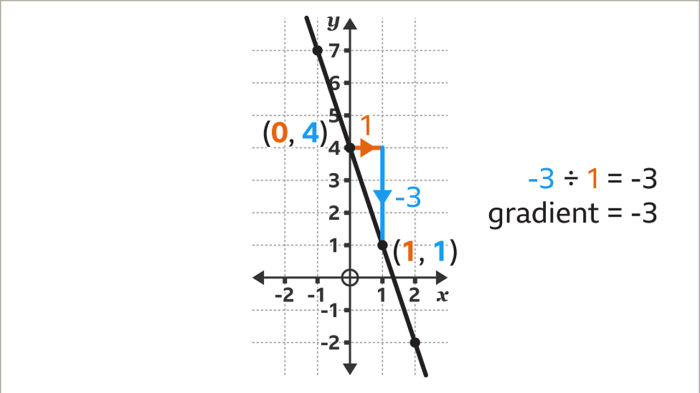
Gradien garis lurus adalah ukuran kemiringan atau kecondongan sebuah garis lurus. Gradien menunjukkan seberapa cepat garis tersebut naik atau turun saat bergerak ke kanan. Dengan kata lain, gradien mengukur perubahan vertikal (y) terhadap perubahan horizontal (x) pada garis tersebut.
Contoh soal gradien garis lurus biasanya muncul dalam pelajaran matematika, khususnya di materi tentang persamaan garis. Nah, kalau kamu sedang mempersiapkan PAS (Penilaian Akhir Semester) kelas 7 semester 1, kamu juga bisa menemukan soal-soal terkait gradien garis lurus di mata pelajaran IPS.
Sebagai contoh, kamu bisa menemukan soal-soal mengenai contoh soal pas kelas 7 semester 1 ips yang membahas tentang pertumbuhan penduduk dan bagaimana gradien garis lurus dapat digunakan untuk menggambarkan tren pertumbuhannya. Jadi, pastikan kamu memahami konsep gradien garis lurus agar bisa menjawab soal-soal PAS dengan baik!
Ilustrasi Gradien Garis Lurus
Gradien garis lurus dapat diilustrasikan dengan beberapa contoh:
- Gradien Positif: Garis yang naik ke kanan memiliki gradien positif. Semakin curam garisnya, semakin besar gradiennya.
- Gradien Negatif: Garis yang turun ke kanan memiliki gradien negatif. Semakin curam garisnya, semakin kecil (atau lebih negatif) gradiennya.
- Gradien Nol: Garis horizontal memiliki gradien nol, karena tidak ada perubahan vertikal (y) saat bergerak ke kanan.
- Gradien Tak Terdefinisi: Garis vertikal memiliki gradien tak terdefinisi, karena perubahan horizontal (x) nya nol, dan kita tidak dapat membagi dengan nol.
Rumus Gradien Garis Lurus
Rumus umum untuk menghitung gradien garis lurus adalah:
m = (y2 – y1) / (x2 – x1)
Dimana:
- m adalah gradien garis lurus
- (x1, y1) adalah koordinat titik pertama pada garis
- (x2, y2) adalah koordinat titik kedua pada garis
Menentukan Gradien dari Dua Titik
Gradien garis lurus merupakan nilai yang menunjukkan kemiringan atau kecondongan garis tersebut. Gradien dapat ditentukan dari persamaan garis, namun juga dapat dihitung jika diketahui dua titik yang dilalui oleh garis tersebut.
Menentukan Gradien dari Dua Titik
Untuk menentukan gradien garis lurus jika diketahui dua titik yang dilalui garis tersebut, kita dapat menggunakan rumus berikut:
m = (y2 – y1) / (x2 – x1)
Dimana:
- m adalah gradien garis
- (x1, y1) adalah koordinat titik pertama
- (x2, y2) adalah koordinat titik kedua
Contoh Soal, Contoh soal gradien garis lurus
Misalkan kita ingin menentukan gradien garis yang melalui titik A (2, 3) dan B (5, 7). Berikut langkah-langkah penyelesaiannya:
- Tentukan koordinat titik pertama (x1, y1) dan titik kedua (x2, y2). Dalam contoh ini, kita dapat memilih titik A sebagai (x1, y1) dan titik B sebagai (x2, y2). Sehingga, x1 = 2, y1 = 3, x2 = 5, dan y2 = 7.
- Substitusikan nilai x1, y1, x2, dan y2 ke dalam rumus gradien.
- Hitung nilai gradien (m).
Berikut perhitungannya:
m = (y2 – y1) / (x2 – x1)
m = (7 – 3) / (5 – 2)
m = 4 / 3
Jadi, gradien garis yang melalui titik A (2, 3) dan B (5, 7) adalah 4/3.
Tabel Rumus, Contoh Soal, dan Langkah Penyelesaian
| Rumus | Contoh Soal | Langkah Penyelesaian |
|---|---|---|
| m = (y2 – y1) / (x2 – x1) | Tentukan gradien garis yang melalui titik A (2, 3) dan B (5, 7). | 1. Tentukan koordinat titik pertama (x1, y1) dan titik kedua (x2, y2). 2. Substitusikan nilai x1, y1, x2, dan y2 ke dalam rumus gradien. 3. Hitung nilai gradien (m). |
Ulasan Penutup
Dengan memahami konsep gradien garis lurus, kita dapat menganalisis dan menyelesaikan berbagai masalah yang berkaitan dengan kemiringan. Mulai dari merancang konstruksi bangunan hingga memahami tren ekonomi, gradien garis lurus menjadi alat yang ampuh untuk memahami dan mengendalikan berbagai aspek kehidupan.




