Contoh soal grafik fungsi linear – Pernahkah Anda bertanya-tanya bagaimana persamaan matematika bisa diubah menjadi gambar yang menarik? Fungsi linear adalah salah satu konsep matematika yang memungkinkan kita melakukan hal tersebut. Dengan mempelajari fungsi linear, kita dapat memahami bagaimana garis lurus terbentuk, bagaimana menentukan titik potongnya, dan bahkan bagaimana menerapkannya dalam kehidupan sehari-hari.
Dalam artikel ini, kita akan menjelajahi dunia grafik fungsi linear dengan membahas berbagai contoh soal yang akan membantu Anda memahami konsep ini dengan lebih baik. Dari pengertian dasar hingga penerapannya dalam berbagai bidang, artikel ini akan menjadi panduan lengkap bagi Anda yang ingin menguasai fungsi linear.
Pengertian Fungsi Linear
Fungsi linear adalah salah satu jenis fungsi yang paling sederhana dan sering dijumpai dalam matematika. Fungsi linear didefinisikan sebagai fungsi yang grafiknya berupa garis lurus. Secara sederhana, fungsi linear menggambarkan hubungan antara dua variabel yang sebanding secara langsung, yaitu jika salah satu variabel meningkat, maka variabel lainnya juga meningkat dengan laju yang tetap.
Contoh Fungsi Linear dalam Kehidupan Sehari-hari
Fungsi linear banyak dijumpai dalam kehidupan sehari-hari. Beberapa contohnya adalah:
- Harga taksi: Tarif taksi biasanya terdiri dari biaya awal dan biaya per kilometer. Biaya total taksi dapat dihitung dengan fungsi linear, di mana biaya awal merupakan konstanta dan biaya per kilometer merupakan koefisien variabel jarak tempuh.
- Gaji karyawan: Gaji karyawan biasanya terdiri dari gaji pokok dan bonus. Gaji total karyawan dapat dihitung dengan fungsi linear, di mana gaji pokok merupakan konstanta dan bonus merupakan koefisien variabel kinerja.
- Biaya telepon: Biaya telepon biasanya terdiri dari biaya bulanan dan biaya per menit. Biaya total telepon dapat dihitung dengan fungsi linear, di mana biaya bulanan merupakan konstanta dan biaya per menit merupakan koefisien variabel waktu.
Tabel Contoh Fungsi Linear dan Persamaannya
Berikut adalah beberapa contoh fungsi linear dan persamaannya:
| Contoh | Persamaan |
|---|---|
| Tarif taksi: Rp 5.000 + Rp 4.000/km | y = 5000 + 4000x |
| Gaji karyawan: Rp 3.000.000 + 10% dari hasil penjualan | y = 3000000 + 0.1x |
| Biaya telepon: Rp 50.000 + Rp 1.000/menit | y = 50000 + 1000x |
Grafik Fungsi Linear: Contoh Soal Grafik Fungsi Linear
Fungsi linear merupakan fungsi yang memiliki bentuk persamaan y = mx + c, dengan m sebagai gradien dan c sebagai konstanta. Grafik fungsi linear adalah garis lurus yang dapat digambar pada bidang kartesius. Grafik fungsi linear memiliki beberapa sifat, yaitu:
- Grafik selalu berbentuk garis lurus.
- Gradien (m) menunjukkan kemiringan garis.
- Konstanta (c) menunjukkan titik potong garis dengan sumbu y.
Cara Menggambar Grafik Fungsi Linear
Untuk menggambar grafik fungsi linear, kita dapat menggunakan dua cara, yaitu:
- Menentukan dua titik pada garis dan menghubungkannya.
- Menentukan titik potong dengan sumbu x dan sumbu y.
Langkah-Langkah Menggambar Grafik Fungsi Linear
Berikut langkah-langkah menggambar grafik fungsi linear dengan contoh:
- Tentukan persamaan fungsi linear yang akan digambar.
- Pilih dua nilai x yang berbeda. Contohnya, x = 0 dan x = 2.
- Substitusikan nilai x ke dalam persamaan fungsi linear untuk mendapatkan nilai y.
- Buat tabel yang berisi titik koordinat (x, y) yang diperoleh.
- Plot titik koordinat pada bidang kartesius.
- Hubungkan kedua titik tersebut dengan garis lurus.
Contoh:
Misalkan persamaan fungsi linearnya adalah y = 2x + 1. Kita akan menentukan dua titik pada garis dengan memilih x = 0 dan x = 2.
- Untuk x = 0, maka y = 2(0) + 1 = 1. Titik koordinatnya adalah (0, 1).
- Untuk x = 2, maka y = 2(2) + 1 = 5. Titik koordinatnya adalah (2, 5).
Kemudian, kita plot kedua titik tersebut pada bidang kartesius dan menghubungkannya dengan garis lurus. Berikut adalah gambar grafik fungsi linear y = 2x + 1:
Gambar grafik fungsi linear y = 2x + 1
Tabel Titik Koordinat pada Grafik Fungsi Linear
| Persamaan Fungsi Linear | Titik Koordinat (x, y) |
|---|---|
| y = x + 2 | (0, 2), (1, 3), (2, 4) |
| y = -2x + 3 | (0, 3), (1, 1), (2, -1) |
| y = 3x – 1 | (0, -1), (1, 2), (2, 5) |
Menentukan Persamaan Fungsi Linear
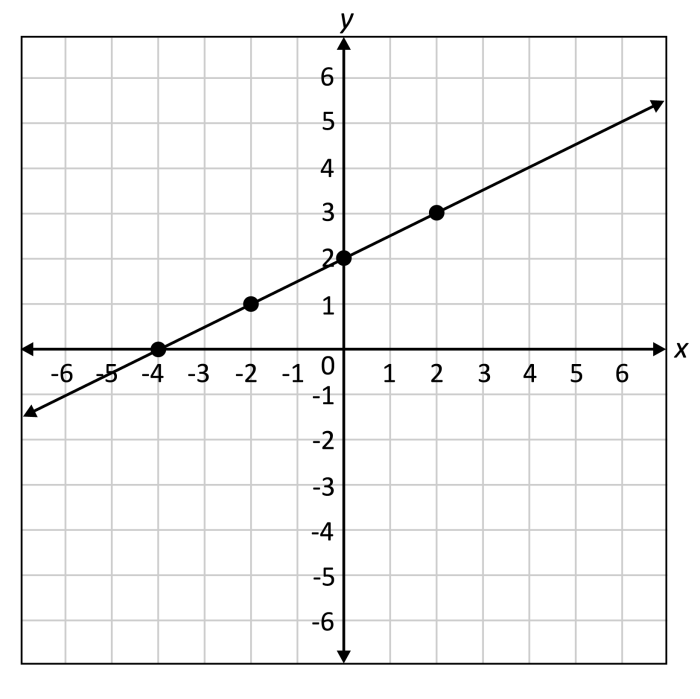
Setelah mempelajari tentang fungsi linear dan grafiknya, selanjutnya kita akan membahas cara menentukan persamaan fungsi linear dari grafiknya. Menentukan persamaan fungsi linear dari grafiknya merupakan langkah penting untuk memahami hubungan antara variabel dan bagaimana variabel tersebut berubah secara linear.
Menentukan Persamaan Fungsi Linear dari Grafik
Untuk menentukan persamaan fungsi linear dari grafiknya, kita perlu memahami bahwa persamaan fungsi linear memiliki bentuk umum y = mx + c, di mana:
- m adalah gradien garis, yang menunjukkan kemiringan garis tersebut.
- c adalah konstanta, yang menunjukkan titik potong garis dengan sumbu y.
Untuk menentukan persamaan fungsi linear, kita perlu mencari nilai m dan c dari grafik.
Langkah-langkah Menentukan Persamaan Fungsi Linear dari Grafik
- Menentukan Gradien (m): Gradien dapat ditentukan dengan memilih dua titik berbeda pada garis dan menghitung selisih ordinat dibagi selisih absisnya. Rumus gradien: m = (y2 – y1) / (x2 – x1).
- Menentukan Konstanta (c): Konstanta dapat ditentukan dengan melihat titik potong garis dengan sumbu y. Titik potong ini memiliki koordinat (0, c). Jika tidak terlihat jelas, kita dapat menggunakan salah satu titik pada garis dan nilai gradien (m) yang sudah diketahui, kemudian mensubstitusikan ke dalam persamaan y = mx + c untuk mencari nilai c.
- Menuliskan Persamaan Fungsi Linear: Setelah nilai m dan c diketahui, kita dapat menuliskan persamaan fungsi linear dalam bentuk y = mx + c.
Contoh Menentukan Persamaan Fungsi Linear dari Grafik
Misalkan kita memiliki grafik fungsi linear yang melewati titik (1, 2) dan (3, 6). Berikut langkah-langkah untuk menentukan persamaan fungsi linearnya:
- Menentukan Gradien (m): m = (6 – 2) / (3 – 1) = 4 / 2 = 2.
- Menentukan Konstanta (c): Kita dapat menggunakan titik (1, 2) dan nilai gradien m = 2 untuk mencari nilai c. Substitusikan nilai-nilai tersebut ke dalam persamaan y = mx + c: 2 = 2(1) + c. Dari persamaan ini, kita dapat memperoleh nilai c = 0.
- Menuliskan Persamaan Fungsi Linear: Dengan nilai m = 2 dan c = 0, persamaan fungsi linearnya adalah y = 2x + 0 atau y = 2x.
Tabel Persamaan Fungsi Linear dan Titik Koordinat pada Grafik, Contoh soal grafik fungsi linear
| Persamaan Fungsi Linear | Titik Koordinat pada Grafik |
|---|---|
| y = x + 2 | (0, 2), (1, 3), (-1, 1) |
| y = -2x + 1 | (0, 1), (1, -1), (-1, 3) |
| y = 3x – 4 | (0, -4), (1, -1), (2, 2) |
Menentukan Titik Potong Grafik Fungsi Linear
Pada pembahasan sebelumnya, kita telah mempelajari bagaimana menentukan persamaan garis lurus. Nah, kali ini kita akan membahas cara menentukan titik potong grafik fungsi linear dengan sumbu x dan sumbu y. Titik potong ini penting karena memberikan informasi tentang di mana grafik fungsi linear memotong sumbu koordinat.
Cara Menentukan Titik Potong
Untuk menentukan titik potong grafik fungsi linear dengan sumbu x dan sumbu y, kita perlu mengingat bahwa:
- Titik potong dengan sumbu x memiliki koordinat (x, 0), artinya nilai y-nya selalu 0.
- Titik potong dengan sumbu y memiliki koordinat (0, y), artinya nilai x-nya selalu 0.
Dengan demikian, untuk menentukan titik potong dengan sumbu x, kita perlu substitusikan nilai y = 0 ke dalam persamaan fungsi linear. Begitu juga untuk menentukan titik potong dengan sumbu y, kita substitusikan nilai x = 0 ke dalam persamaan fungsi linear.
Contoh Penentuan Titik Potong
Misalnya, kita memiliki persamaan fungsi linear y = 2x + 3. Untuk menentukan titik potong dengan sumbu x, kita substitusikan y = 0 ke dalam persamaan:
0 = 2x + 3
Kemudian, kita selesaikan persamaan tersebut untuk mencari nilai x:
2x = -3
x = -3/2
Jadi, titik potong dengan sumbu x adalah (-3/2, 0).
Selanjutnya, untuk menentukan titik potong dengan sumbu y, kita substitusikan x = 0 ke dalam persamaan:
y = 2(0) + 3
y = 3
Jadi, titik potong dengan sumbu y adalah (0, 3).
Tabel Titik Potong
Berikut tabel yang berisi beberapa persamaan fungsi linear dan titik potongnya dengan sumbu x dan sumbu y:
| Persamaan Fungsi Linear | Titik Potong Sumbu x | Titik Potong Sumbu y |
|---|---|---|
| y = 2x + 1 | (-1/2, 0) | (0, 1) |
| y = -x + 4 | (4, 0) | (0, 4) |
| y = 3x – 2 | (2/3, 0) | (0, -2) |
Penerapan Fungsi Linear
Fungsi linear merupakan konsep matematika yang sering kita temui dalam kehidupan sehari-hari. Penerapannya begitu luas, mulai dari menghitung biaya parkir, menghitung jarak tempuh, hingga menentukan keuntungan dalam suatu bisnis. Dalam artikel ini, kita akan menjelajahi berbagai contoh penerapan fungsi linear dalam kehidupan nyata dan mempelajari bagaimana konsep ini dapat membantu kita menyelesaikan masalah-masalah praktis.
Contoh Penerapan Fungsi Linear dalam Kehidupan Sehari-hari
Fungsi linear dapat ditemukan dalam berbagai aspek kehidupan kita. Berikut adalah beberapa contohnya:
- Biaya Parkir: Di banyak tempat parkir, biaya parkir ditentukan berdasarkan waktu parkir. Misalkan, biaya parkir Rp5.000,- untuk jam pertama dan Rp2.000,- untuk setiap jam berikutnya. Dalam kasus ini, biaya parkir dapat diwakili oleh fungsi linear dengan persamaan y = 2000x + 5000, di mana y adalah total biaya parkir dan x adalah jumlah jam parkir setelah jam pertama.
- Jarak Tempuh: Ketika kita berkendara dengan kecepatan konstan, jarak yang ditempuh sebanding dengan waktu tempuh. Misalkan, kita berkendara dengan kecepatan 60 km/jam. Jarak yang ditempuh dalam waktu t jam dapat dihitung dengan persamaan y = 60t, di mana y adalah jarak tempuh dan t adalah waktu tempuh.
- Keuntungan Bisnis: Dalam bisnis, keuntungan seringkali dihitung dengan menggunakan fungsi linear. Misalnya, sebuah toko menjual baju dengan harga Rp100.000,- per potong dan biaya produksi per potong adalah Rp60.000,-. Keuntungan per potong dapat dihitung dengan persamaan y = 100000 – 60000 = 40000, di mana y adalah keuntungan dan x adalah jumlah baju yang terjual.
Contoh Soal Cerita dan Penyelesaiannya
Sebuah perusahaan taksi menetapkan tarif awal Rp5.000,- dan biaya per kilometer Rp3.000,-. Tentukan persamaan fungsi linear yang menyatakan hubungan antara jarak tempuh dan biaya taksi. Berapa biaya taksi jika jarak tempuh 10 kilometer?
Contoh soal grafik fungsi linear sering kita jumpai dalam pelajaran matematika, seperti menentukan titik potong sumbu x dan y. Nah, konsep ini ternyata juga erat kaitannya dengan ilmu ekonomi, khususnya dalam optimasi ekonomi manajerial. Misalnya, dalam menentukan jumlah produksi optimal untuk memaksimalkan keuntungan, kita bisa menggunakan grafik fungsi linear untuk menggambarkan hubungan antara biaya, pendapatan, dan keuntungan.
Untuk mempelajari lebih lanjut tentang contoh soal optimasi ekonomi manajerial dan jawabannya, kamu bisa mengunjungi link ini. Jadi, selain membantu memahami konsep matematika, contoh soal grafik fungsi linear juga bisa diterapkan dalam berbagai bidang, termasuk ekonomi.
Berikut langkah-langkah untuk menyelesaikan soal cerita tersebut:
- Menentukan variabel: Misalkan x adalah jarak tempuh (dalam kilometer) dan y adalah biaya taksi (dalam rupiah).
- Menentukan persamaan fungsi linear: Biaya taksi terdiri dari tarif awal dan biaya per kilometer. Persamaan fungsi linear yang menyatakan hubungan antara jarak tempuh dan biaya taksi adalah y = 3000x + 5000.
- Menghitung biaya taksi untuk jarak tempuh 10 kilometer: Substitusikan x = 10 ke dalam persamaan fungsi linear. y = 3000(10) + 5000 = 35000. Jadi, biaya taksi untuk jarak tempuh 10 kilometer adalah Rp35.000,-.
Penerapan Fungsi Linear dalam Berbagai Bidang
| Bidang | Contoh Penerapan Fungsi Linear |
|---|---|
| Matematika | Menghitung gradien garis, menentukan persamaan garis, menyelesaikan sistem persamaan linear. |
| Fisika | Menghitung kecepatan dan percepatan, menentukan hubungan antara jarak, waktu, dan kecepatan. |
| Ekonomi | Menghitung keuntungan dan kerugian, menentukan hubungan antara harga dan permintaan. |
| Statistika | Menghitung rata-rata dan median, menentukan hubungan antara variabel. |
Pembahasan Soal Grafik Fungsi Linear
Grafik fungsi linear merupakan representasi visual dari persamaan linear yang menggambarkan hubungan antara dua variabel. Membuat dan menganalisis grafik fungsi linear merupakan keterampilan penting dalam matematika, karena membantu kita memahami pola dan tren dalam data. Dalam pembahasan ini, kita akan mengkaji beberapa contoh soal grafik fungsi linear yang menantang dan menjelaskan langkah-langkah penyelesaiannya secara detail.
Menentukan Persamaan Garis dari Dua Titik yang Diketahui
Salah satu tantangan dalam grafik fungsi linear adalah menentukan persamaan garis dari dua titik yang diketahui. Untuk menyelesaikan masalah ini, kita perlu memahami konsep gradien dan titik potong sumbu y. Gradien (m) merupakan ukuran kemiringan garis, yang dapat dihitung dengan rumus:
m = (y2 – y1) / (x2 – x1)
Titik potong sumbu y (b) adalah titik di mana garis memotong sumbu y. Setelah kita mengetahui gradien dan titik potong sumbu y, kita dapat menuliskan persamaan garis dalam bentuk slope-intercept:
y = mx + b
Berikut adalah langkah-langkah yang dapat digunakan untuk menentukan persamaan garis dari dua titik yang diketahui:
- Tentukan gradien (m) menggunakan rumus gradien.
- Pilih salah satu titik yang diketahui dan substitusikan nilai x dan y ke dalam persamaan slope-intercept (y = mx + b). Selesaikan persamaan untuk mencari nilai b.
- Ganti nilai m dan b ke dalam persamaan slope-intercept untuk mendapatkan persamaan garis.
Menentukan Persamaan Garis yang Melalui Titik Tertentu dan Sejajar dengan Garis Lain
Tantangan lain yang sering muncul adalah menentukan persamaan garis yang melalui titik tertentu dan sejajar dengan garis lain. Dua garis sejajar memiliki gradien yang sama. Berikut adalah langkah-langkah untuk menyelesaikan masalah ini:
- Tentukan gradien (m) dari garis yang diketahui.
- Gunakan gradien yang sama (m) dan titik yang diketahui untuk menentukan persamaan garis menggunakan persamaan slope-intercept (y = mx + b). Substitusikan nilai x dan y dari titik yang diketahui ke dalam persamaan dan selesaikan untuk b.
- Ganti nilai m dan b ke dalam persamaan slope-intercept untuk mendapatkan persamaan garis yang sejajar.
Menentukan Persamaan Garis yang Melalui Titik Tertentu dan Tegak Lurus dengan Garis Lain
Dua garis tegak lurus memiliki gradien yang saling berlawanan dan terbalik. Jika gradien garis pertama adalah m, maka gradien garis kedua adalah -1/m. Berikut adalah langkah-langkah untuk menentukan persamaan garis yang melalui titik tertentu dan tegak lurus dengan garis lain:
- Tentukan gradien (m) dari garis yang diketahui.
- Hitung gradien garis tegak lurus dengan rumus -1/m.
- Gunakan gradien tegak lurus (m) dan titik yang diketahui untuk menentukan persamaan garis menggunakan persamaan slope-intercept (y = mx + b). Substitusikan nilai x dan y dari titik yang diketahui ke dalam persamaan dan selesaikan untuk b.
- Ganti nilai m dan b ke dalam persamaan slope-intercept untuk mendapatkan persamaan garis yang tegak lurus.
Menentukan Persamaan Garis dari Grafik
Menentukan persamaan garis dari grafik merupakan keterampilan penting dalam memahami hubungan antara variabel. Untuk menyelesaikan masalah ini, kita perlu mengidentifikasi gradien dan titik potong sumbu y dari grafik. Berikut adalah langkah-langkah untuk menentukan persamaan garis dari grafik:
- Pilih dua titik yang terletak pada garis.
- Hitung gradien (m) menggunakan rumus gradien.
- Identifikasi titik potong sumbu y (b) dari grafik.
- Ganti nilai m dan b ke dalam persamaan slope-intercept (y = mx + b) untuk mendapatkan persamaan garis.
Contoh Soal dan Penyelesaian
| Soal | Langkah Penyelesaian | Penjelasan |
|---|---|---|
| Tentukan persamaan garis yang melalui titik (2, 3) dan (4, 7). | 1. Hitung gradien: m = (7 – 3) / (4 – 2) = 2 2. Substitusikan titik (2, 3) dan gradien m = 2 ke dalam persamaan slope-intercept: 3 = 2(2) + b. Selesaikan untuk b: b = -1 3. Persamaan garis: y = 2x – 1 |
Gradien dihitung menggunakan rumus gradien. Titik potong sumbu y dihitung dengan mensubstitusikan nilai x dan y dari titik yang diketahui ke dalam persamaan slope-intercept. |
| Tentukan persamaan garis yang melalui titik (1, 2) dan sejajar dengan garis y = 3x + 5. | 1. Gradien garis yang diketahui: m = 3 2. Substitusikan titik (1, 2) dan gradien m = 3 ke dalam persamaan slope-intercept: 2 = 3(1) + b. Selesaikan untuk b: b = -1 3. Persamaan garis sejajar: y = 3x – 1 |
Dua garis sejajar memiliki gradien yang sama. Titik potong sumbu y dihitung dengan mensubstitusikan nilai x dan y dari titik yang diketahui ke dalam persamaan slope-intercept. |
| Tentukan persamaan garis yang melalui titik (3, 4) dan tegak lurus dengan garis y = -2x + 1. | 1. Gradien garis yang diketahui: m = -2 2. Gradien garis tegak lurus: m = 1/2 3. Substitusikan titik (3, 4) dan gradien m = 1/2 ke dalam persamaan slope-intercept: 4 = (1/2)(3) + b. Selesaikan untuk b: b = 5/2 4. Persamaan garis tegak lurus: y = (1/2)x + 5/2 |
Dua garis tegak lurus memiliki gradien yang saling berlawanan dan terbalik. Titik potong sumbu y dihitung dengan mensubstitusikan nilai x dan y dari titik yang diketahui ke dalam persamaan slope-intercept. |
Ringkasan Penutup
Melalui contoh soal yang beragam, Anda telah mendapatkan pemahaman yang lebih dalam tentang fungsi linear. Anda kini siap untuk menghadapi berbagai jenis soal, baik dalam bentuk latihan maupun ujian. Ingat, kunci untuk menguasai fungsi linear terletak pada pemahaman konsep dasar dan latihan yang konsisten.




