Contoh Soal Grafik Persamaan Garis Lurus dan Jawabannya: Menguak Rahasia Garis Lurus

Pernahkah Anda bertanya-tanya bagaimana persamaan garis lurus dapat menggambarkan berbagai situasi dalam kehidupan? Contoh Soal Grafik Persamaan Garis Lurus dan Jawabannya akan membawa Anda menjelajahi dunia garis lurus, mulai dari definisinya hingga aplikasi praktisnya.

Melalui contoh-contoh soal yang menarik, Anda akan belajar cara menentukan persamaan garis lurus, memahami hubungan antara gradien dan titik potong sumbu y, serta mengaplikasikan konsep ini dalam berbagai bidang, seperti ekonomi, teknik, dan bisnis.

Pengertian Persamaan Garis Lurus

Persamaan garis lurus adalah sebuah persamaan matematika yang menggambarkan hubungan antara variabel-variabel yang menentukan suatu garis lurus pada bidang kartesius.

Definisi Persamaan Garis Lurus

Persamaan garis lurus merupakan representasi aljabar dari garis lurus pada bidang kartesius. Persamaan ini menunjukkan hubungan antara koordinat x dan y dari setiap titik yang terletak pada garis tersebut.

Contoh Persamaan Garis Lurus

Sebagai contoh, persamaan garis lurus y = 2x + 1 menunjukkan bahwa untuk setiap nilai x, nilai y dapat dihitung dengan mengalikan x dengan 2 dan kemudian menambahkan 1.

Contohnya, jika x = 2, maka y = 2(2) + 1 = 5. Artinya, titik (2, 5) terletak pada garis lurus yang diwakili oleh persamaan tersebut.

Bentuk Umum Persamaan Garis Lurus

Persamaan garis lurus memiliki beberapa bentuk umum, di antaranya:

Bentuk Umum	Variabel	Keterangan
y = mx + c	m: Gradien garis c: Konstanta atau titik potong sumbu y	Bentuk paling umum, mudah untuk menentukan gradien dan titik potong sumbu y.
ax + by + c = 0	a, b, c: Konstanta	Bentuk umum yang lebih fleksibel, memungkinkan untuk menentukan persamaan garis lurus dengan berbagai cara.
(y – y1) = m(x – x1)	m: Gradien garis (x1, y1): Titik yang terletak pada garis	Bentuk yang digunakan untuk menentukan persamaan garis lurus dengan menggunakan gradien dan titik yang diketahui.

Menentukan Persamaan Garis Lurus

Persamaan garis lurus merupakan representasi aljabar dari garis yang menggambarkan hubungan antara variabel x dan y pada bidang kartesius. Untuk menentukan persamaan garis lurus, kita perlu memahami konsep gradien dan titik potong sumbu y. Gradien (m) menunjukkan kemiringan garis, sedangkan titik potong sumbu y (b) menunjukkan titik di mana garis memotong sumbu y.

Menentukan Persamaan Garis Lurus dengan Dua Titik yang Diketahui

Jika kita diberikan dua titik pada garis lurus, kita dapat menentukan persamaan garis lurus dengan menggunakan rumus berikut:

m = (y2 – y1) / (x2 – x1)

Dimana:

• m adalah gradien garis
• (x1, y1) dan (x2, y2) adalah koordinat dari dua titik yang diketahui

Setelah mendapatkan nilai gradien (m), kita dapat menggunakan salah satu titik yang diketahui dan rumus persamaan garis lurus berikut untuk menentukan persamaan garis lurus:

y – y1 = m(x – x1)

Dimana:

• m adalah gradien garis
• (x1, y1) adalah koordinat salah satu titik yang diketahui

Menentukan Persamaan Garis Lurus dengan Gradien dan Titik yang Diketahui

Jika kita sudah mengetahui gradien (m) garis lurus dan satu titik (x1, y1) yang dilalui garis tersebut, kita dapat langsung menggunakan rumus persamaan garis lurus berikut:

y – y1 = m(x – x1)

Dimana:

• m adalah gradien garis
• (x1, y1) adalah koordinat titik yang diketahui

Menentukan Persamaan Garis Lurus dengan Gradien dan Titik Potong Sumbu Y

Jika kita sudah mengetahui gradien (m) dan titik potong sumbu y (b) dari garis lurus, kita dapat langsung menggunakan rumus persamaan garis lurus berikut:

y = mx + b

Dimana:

• m adalah gradien garis
• b adalah titik potong sumbu y

Mengenali Grafik Persamaan Garis Lurus

Grafik persamaan garis lurus adalah representasi visual dari persamaan garis lurus. Dengan memahami ciri-ciri grafik ini, kita dapat dengan mudah menentukan persamaan garisnya dan memahami hubungan antara berbagai elemen dalam persamaan tersebut.

Ciri-ciri Grafik Persamaan Garis Lurus

Grafik persamaan garis lurus memiliki ciri-ciri khas yang membedakannya dari grafik fungsi lain. Berikut adalah beberapa ciri utama:

• Bentuk garis lurus: Grafik persamaan garis lurus selalu berbentuk garis lurus, tidak melengkung atau berputar-putar.
• Konstanta kemiringan: Garis lurus memiliki kemiringan yang konstan. Kemiringan ini menunjukkan seberapa curam atau landai garis tersebut. Kemiringan positif menunjukkan garis miring ke atas, kemiringan negatif menunjukkan garis miring ke bawah, dan kemiringan nol menunjukkan garis horizontal.
• Titik potong sumbu y: Garis lurus selalu memotong sumbu y pada satu titik. Titik potong sumbu y ini menunjukkan nilai y ketika nilai x adalah 0.

Contoh Grafik Persamaan Garis Lurus, Contoh soal grafik persamaan garis lurus dan jawabannya

Berikut adalah beberapa contoh grafik persamaan garis lurus dengan berbagai kemiringan dan titik potong sumbu y:

• Garis dengan kemiringan positif dan titik potong sumbu y positif: Grafik ini akan miring ke atas dan memotong sumbu y di atas titik 0. Contohnya, persamaan y = 2x + 3 memiliki kemiringan 2 dan titik potong sumbu y 3.
• Garis dengan kemiringan negatif dan titik potong sumbu y negatif: Grafik ini akan miring ke bawah dan memotong sumbu y di bawah titik 0. Contohnya, persamaan y = -x – 2 memiliki kemiringan -1 dan titik potong sumbu y -2.
• Garis dengan kemiringan nol dan titik potong sumbu y positif: Grafik ini akan berupa garis horizontal dan memotong sumbu y di atas titik 0. Contohnya, persamaan y = 4 memiliki kemiringan 0 dan titik potong sumbu y 4.
• Garis dengan kemiringan tak terdefinisi dan titik potong sumbu y tidak ada: Grafik ini akan berupa garis vertikal dan tidak memotong sumbu y. Contohnya, persamaan x = 2 memiliki kemiringan tak terdefinisi dan tidak memiliki titik potong sumbu y.

Hubungan Antara Gradien, Titik Potong Sumbu Y, dan Bentuk Persamaan Garis Lurus

Bentuk umum persamaan garis lurus adalah y = mx + c, di mana:

• m adalah gradien garis, yang menunjukkan kemiringan garis.
• c adalah titik potong sumbu y, yang menunjukkan titik di mana garis memotong sumbu y.

Dengan demikian, gradien dan titik potong sumbu y menentukan bentuk persamaan garis lurus. Jika kita mengetahui gradien dan titik potong sumbu y, kita dapat langsung menuliskan persamaan garisnya.

Contohnya, jika gradien garis adalah 3 dan titik potong sumbu y adalah -1, maka persamaan garisnya adalah y = 3x – 1.

Mempelajari contoh soal grafik persamaan garis lurus dan jawabannya memang penting, terutama buat kamu yang lagi belajar matematika. Nah, selain itu, kamu juga bisa belajar soal-soal di bidang lain, misalnya contoh soal dan jawaban laporan keuangan perusahaan dagang, seperti yang bisa kamu temukan di situs ini.

Keduanya sama-sama penting, lho! Nggak cuma soal persamaan garis lurus, memahami laporan keuangan juga penting buat kamu yang mau berkecimpung di dunia bisnis.

Soal-Soal Grafik Persamaan Garis Lurus

Persamaan garis lurus merupakan salah satu konsep dasar dalam matematika yang penting untuk dipahami. Dalam artikel ini, kita akan membahas contoh-contoh soal grafik persamaan garis lurus dengan tingkat kesulitan yang berbeda. Tujuannya adalah untuk membantu kamu memahami bagaimana cara menyelesaikan soal-soal tersebut dan mengaplikasikannya dalam berbagai situasi.

Contoh Soal 1: Menentukan Persamaan Garis Lurus

Misalkan kita diberikan dua titik pada sebuah garis, yaitu (2, 3) dan (4, 7). Bagaimana cara menentukan persamaan garis lurus yang melalui kedua titik tersebut?

1. Menentukan Gradien (m): Gradien merupakan kemiringan garis dan dapat dihitung dengan rumus:
   

   m = (y2 – y1) / (x2 – x1)

   Dalam contoh ini, kita punya (x1, y1) = (2, 3) dan (x2, y2) = (4, 7).
   Sehingga, gradiennya adalah:

   m = (7 – 3) / (4 – 2) = 4 / 2 = 2

2. Menentukan Persamaan Garis: Setelah mendapatkan gradien, kita dapat menggunakan salah satu bentuk persamaan garis lurus, yaitu:
   

   y – y1 = m(x – x1)

   Kita bisa menggunakan salah satu titik yang diberikan, misalnya (2, 3). Dengan memasukkan nilai gradien (m = 2) dan titik (2, 3) ke dalam persamaan, kita dapatkan:

   y – 3 = 2(x – 2)

   Sederhanakan persamaan tersebut:

   y – 3 = 2x – 4

   y = 2x – 1

   Jadi, persamaan garis lurus yang melalui titik (2, 3) dan (4, 7) adalah y = 2x – 1.

Contoh Soal 2: Menentukan Titik Potong dengan Sumbu Koordinat

Persamaan garis lurus adalah y = -3x + 6. Bagaimana cara menentukan titik potong garis tersebut dengan sumbu x dan sumbu y?

1. Titik Potong Sumbu x: Titik potong dengan sumbu x terjadi ketika nilai y = 0.
   Substitusikan y = 0 ke dalam persamaan garis:

   0 = -3x + 6

   Selesaikan persamaan untuk mencari nilai x:

   3x = 6

   x = 2

   Jadi, titik potong dengan sumbu x adalah (2, 0).

2. Titik Potong Sumbu y: Titik potong dengan sumbu y terjadi ketika nilai x = 0.
   Substitusikan x = 0 ke dalam persamaan garis:

   y = -3(0) + 6

   y = 6

   Jadi, titik potong dengan sumbu y adalah (0, 6).

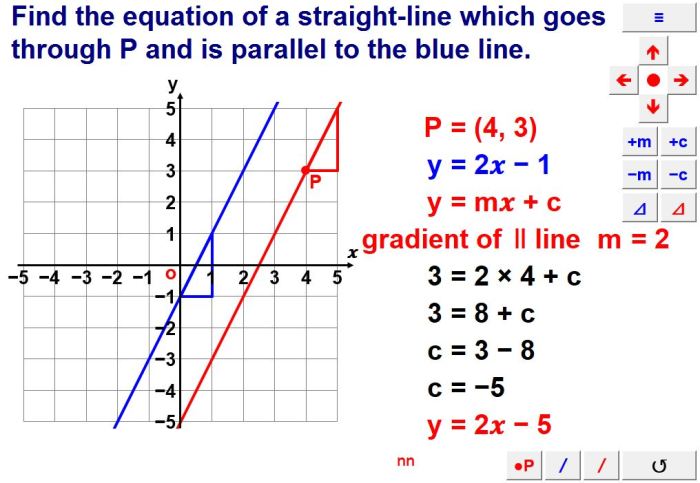
Contoh Soal 3: Menentukan Persamaan Garis Sejajar

Diketahui persamaan garis lurus y = 4x – 2. Bagaimana cara menentukan persamaan garis sejajar yang melalui titik (1, 5)?

1. Menentukan Gradien: Garis sejajar memiliki gradien yang sama.
   Jadi, gradien garis sejajar juga sama dengan gradien garis awal, yaitu 4.
2. Menentukan Persamaan Garis Sejajar: Gunakan titik (1, 5) dan gradien m = 4 dalam bentuk persamaan garis y – y1 = m(x – x1):
   

   y – 5 = 4(x – 1)

   Sederhanakan persamaan:

   y – 5 = 4x – 4

   y = 4x + 1

   Jadi, persamaan garis sejajar yang melalui titik (1, 5) adalah y = 4x + 1.

Contoh Soal 4: Menentukan Persamaan Garis Tegak Lurus

Diketahui persamaan garis lurus y = -2x + 3. Bagaimana cara menentukan persamaan garis tegak lurus yang melalui titik (2, 1)?

1. Menentukan Gradien: Garis tegak lurus memiliki gradien yang merupakan negatif kebalikan dari gradien garis awal.
   Gradien garis awal adalah -2, jadi gradien garis tegak lurus adalah 1/2.
2. Menentukan Persamaan Garis Tegak Lurus: Gunakan titik (2, 1) dan gradien m = 1/2 dalam bentuk persamaan garis y – y1 = m(x – x1):
   

   y – 1 = 1/2(x – 2)

   Sederhanakan persamaan:

   y – 1 = 1/2x – 1

   y = 1/2x

   Jadi, persamaan garis tegak lurus yang melalui titik (2, 1) adalah y = 1/2x.

Contoh Soal 5: Menggambar Grafik Persamaan Garis Lurus

Bagaimana cara menggambar grafik persamaan garis lurus y = -x + 4?

1. Menentukan Dua Titik: Pilih dua nilai x dan substitusikan ke dalam persamaan untuk mendapatkan nilai y yang sesuai.
   Misalnya, untuk x = 0, y = -0 + 4 = 4.
   Jadi, titik pertama adalah (0, 4).
   Untuk x = 2, y = -2 + 4 = 2.
   Jadi, titik kedua adalah (2, 2).
2. Menggambar Garis: Plot kedua titik yang diperoleh pada bidang koordinat.
   Hubungkan kedua titik tersebut dengan garis lurus.
   Garis yang tergambar adalah grafik persamaan y = -x + 4.

Aplikasi Persamaan Garis Lurus dalam Kehidupan Sehari-hari: Contoh Soal Grafik Persamaan Garis Lurus Dan Jawabannya

Persamaan garis lurus, meskipun terlihat sederhana, memiliki aplikasi yang luas dalam berbagai aspek kehidupan sehari-hari. Dari menghitung biaya parkir hingga memprediksi pertumbuhan ekonomi, persamaan garis lurus memberikan kerangka kerja yang berguna untuk memahami dan menyelesaikan masalah praktis.

Contoh Aplikasi Persamaan Garis Lurus

Berikut adalah beberapa contoh aplikasi persamaan garis lurus dalam kehidupan sehari-hari:

• Menghitung Biaya Parkir: Bayangkan Anda sedang berbelanja di sebuah mal yang menerapkan tarif parkir berdasarkan waktu. Tarif parkir umumnya terdiri dari biaya dasar dan biaya tambahan per jam. Persamaan garis lurus dapat digunakan untuk menghitung total biaya parkir berdasarkan lama waktu parkir. Misalnya, jika biaya dasar Rp5.000 dan biaya per jam Rp2.000, persamaan garis lurus yang mewakili total biaya parkir adalah:
  

  Total Biaya = Biaya Dasar + (Biaya Per Jam x Lama Waktu Parkir)

  Dengan menggunakan persamaan ini, Anda dapat dengan mudah menghitung total biaya parkir untuk jangka waktu tertentu.

• Memprediksi Pertumbuhan Ekonomi: Ekonomi suatu negara biasanya menunjukkan pola pertumbuhan tertentu dari waktu ke waktu. Persamaan garis lurus dapat digunakan untuk memprediksi pertumbuhan ekonomi di masa depan berdasarkan data pertumbuhan ekonomi di masa lalu. Misalnya, jika pertumbuhan ekonomi suatu negara rata-rata 5% per tahun selama 5 tahun terakhir, persamaan garis lurus dapat digunakan untuk memprediksi pertumbuhan ekonomi pada tahun berikutnya. Namun, perlu diingat bahwa prediksi ini hanya berdasarkan tren masa lalu dan mungkin tidak selalu akurat karena faktor-faktor lain yang dapat memengaruhi pertumbuhan ekonomi.
• Menghitung Kecepatan Kendaraan: Kecepatan kendaraan dapat dihitung menggunakan persamaan garis lurus. Persamaan garis lurus yang mewakili kecepatan kendaraan adalah:
  

  Kecepatan = Jarak / Waktu

  Misalnya, jika sebuah mobil menempuh jarak 100 km dalam waktu 2 jam, kecepatan mobil tersebut adalah 50 km/jam. Persamaan garis lurus ini juga dapat digunakan untuk menghitung jarak yang ditempuh kendaraan berdasarkan kecepatan dan waktu tempuh.

Hubungan Aplikasi Persamaan Garis Lurus dengan Bidang Ilmu atau Profesi

Aplikasi Persamaan Garis Lurus	Bidang Ilmu/Profesi
Menghitung Biaya Parkir	Manajemen Bisnis, Ekonomi
Memprediksi Pertumbuhan Ekonomi	Ekonomi, Statistik
Menghitung Kecepatan Kendaraan	Fisika, Teknik

Keterampilan dalam Menyelesaikan Soal Grafik Persamaan Garis Lurus

Menguasai persamaan garis lurus dan kemampuan untuk menggambar grafiknya adalah kunci untuk memahami konsep dasar dalam matematika. Untuk menyelesaikan soal-soal yang melibatkan grafik persamaan garis lurus, kamu membutuhkan beberapa keterampilan penting yang perlu diasah. Artikel ini akan membahas beberapa keterampilan penting dan strategi yang dapat kamu gunakan untuk meningkatkan kemampuanmu dalam menyelesaikan soal-soal tersebut.

Memahami Konsep Dasar Persamaan Garis Lurus

Sebelum kamu bisa menyelesaikan soal grafik persamaan garis lurus, kamu perlu memahami konsep dasarnya. Persamaan garis lurus umumnya ditulis dalam bentuk y = mx + c, di mana:

• y adalah ordinat (nilai pada sumbu vertikal)
• x adalah absis (nilai pada sumbu horizontal)
• m adalah gradien garis, yang menunjukkan kemiringan garis. Gradien positif menunjukkan garis naik ke kanan, gradien negatif menunjukkan garis turun ke kanan, dan gradien nol menunjukkan garis horizontal.
• c adalah konstanta, yang menunjukkan titik potong garis dengan sumbu vertikal (titik di mana garis memotong sumbu y).

Mengenali dan Menentukan Gradien dan Titik Potong

Kemampuan untuk mengenali dan menentukan gradien dan titik potong dari persamaan garis lurus sangat penting. Berikut adalah beberapa tips untuk melakukannya:

• Gradien: Jika persamaan garis lurus sudah dalam bentuk y = mx + c, maka gradien (m) langsung terlihat. Jika persamaan tidak dalam bentuk ini, kamu perlu mengubahnya menjadi bentuk y = mx + c terlebih dahulu.
• Titik Potong: Titik potong dengan sumbu y (c) juga langsung terlihat jika persamaan dalam bentuk y = mx + c. Jika tidak, kamu bisa mencari titik potong dengan mengganti x dengan 0 dalam persamaan dan menyelesaikan untuk y.

Membuat Grafik Persamaan Garis Lurus

Setelah memahami konsep dasar dan mampu mengenali gradien dan titik potong, kamu siap untuk membuat grafik persamaan garis lurus. Berikut adalah langkah-langkah yang dapat kamu ikuti:

1. Tentukan titik potong dengan sumbu y (c). Titik ini akan berada pada sumbu vertikal.
2. Gunakan gradien (m) untuk menemukan titik lain pada garis. Gradien menunjukkan kemiringan garis, jadi untuk setiap langkah ke kanan, kamu perlu naik atau turun sesuai dengan nilai gradien. Misalnya, jika gradien adalah 2, maka untuk setiap langkah ke kanan, kamu naik 2 langkah ke atas.
3. Hubungkan kedua titik yang telah kamu temukan. Garis yang terhubung kedua titik ini adalah grafik persamaan garis lurus.

Strategi untuk Menghindari Kesalahan Umum

Saat menyelesaikan soal grafik persamaan garis lurus, beberapa kesalahan umum yang sering terjadi. Berikut adalah beberapa strategi untuk menghindarinya:

• Perhatikan tanda gradien. Pastikan kamu memahami bahwa gradien positif menunjukkan garis naik ke kanan, sedangkan gradien negatif menunjukkan garis turun ke kanan.
• Pastikan kamu menggunakan skala yang benar saat menggambar grafik. Jika skala tidak tepat, grafik akan menjadi tidak akurat.
• Latih dengan berbagai jenis soal. Semakin banyak soal yang kamu kerjakan, semakin terbiasa kamu dalam memahami konsep dan menghindari kesalahan.

Menghubungkan Grafik Persamaan Garis Lurus dengan Konsep Lain

Grafik persamaan garis lurus bukan hanya sekadar gambar garis lurus. Di baliknya, tersembunyi hubungan erat dengan konsep-konsep penting dalam matematika, seperti sistem persamaan linear dan fungsi linear. Pemahaman tentang hubungan ini akan membuka cakrawala baru dalam menyelesaikan masalah matematika yang lebih kompleks.

Sistem Persamaan Linear

Grafik persamaan garis lurus dapat digunakan untuk menyelesaikan sistem persamaan linear. Setiap persamaan dalam sistem tersebut akan direpresentasikan oleh sebuah garis lurus pada grafik. Titik potong antara kedua garis tersebut merupakan solusi dari sistem persamaan linear.

• Contohnya, jika kita memiliki sistem persamaan linear 2x + y = 5 dan x – y = 1, kita dapat menggambar kedua persamaan tersebut pada grafik. Titik potong antara kedua garis tersebut adalah (2, 1), yang merupakan solusi dari sistem persamaan linear.

Fungsi Linear

Grafik persamaan garis lurus juga dapat digunakan untuk menggambarkan fungsi linear. Fungsi linear adalah fungsi yang memiliki bentuk y = mx + c, di mana m adalah kemiringan garis dan c adalah titik potong dengan sumbu y. Grafik fungsi linear akan berupa garis lurus yang memiliki kemiringan dan titik potong dengan sumbu y yang sesuai.

• Contohnya, fungsi linear y = 2x + 1 akan memiliki grafik berupa garis lurus yang memiliki kemiringan 2 dan titik potong dengan sumbu y di (0, 1).

Contoh Soal

Berikut adalah contoh soal yang menggabungkan konsep grafik persamaan garis lurus dengan konsep lain:

Sebuah toko menjual dua jenis barang, yaitu A dan B. Harga barang A adalah Rp10.000 per unit dan harga barang B adalah Rp15.000 per unit. Seorang pembeli ingin membeli barang A dan B dengan total biaya Rp100.000. Berapa banyak unit barang A dan B yang dapat dibeli oleh pembeli tersebut?

Untuk menyelesaikan soal ini, kita dapat menggunakan konsep grafik persamaan garis lurus. Misalkan x adalah jumlah unit barang A dan y adalah jumlah unit barang B. Maka persamaan yang menggambarkan total biaya adalah 10000x + 15000y = 100000. Persamaan ini dapat diubah menjadi bentuk y = -2/3x + 10/3. Grafik dari persamaan ini akan berupa garis lurus.

Untuk menemukan solusi dari soal ini, kita perlu mencari titik-titik pada garis lurus yang memiliki koordinat x dan y yang merupakan bilangan bulat. Titik-titik tersebut mewakili jumlah unit barang A dan B yang dapat dibeli oleh pembeli tersebut.

Penggunaan Alat Bantu dalam Menganalisis Grafik Persamaan Garis Lurus

Dalam mempelajari grafik persamaan garis lurus, penggunaan alat bantu dapat sangat membantu dalam mempermudah analisis dan penyelesaian masalah. Alat bantu ini tidak hanya mempercepat proses, tetapi juga meningkatkan keakuratan dan pemahaman konsep. Alat bantu yang umum digunakan meliputi kalkulator, software matematika, dan aplikasi grafis.

Fungsi dan Penggunaan Alat Bantu

Alat bantu memiliki fungsi yang beragam dalam analisis grafik persamaan garis lurus. Kalkulator dapat membantu dalam menghitung nilai-nilai yang dibutuhkan, seperti titik potong sumbu x dan y, serta kemiringan garis. Software matematika, seperti GeoGebra atau Desmos, memungkinkan visualisasi grafik dengan lebih detail dan interaktif. Aplikasi grafis, seperti Microsoft Excel, dapat digunakan untuk membuat grafik dan menganalisis data yang berhubungan dengan persamaan garis lurus.

Contoh Penggunaan Alat Bantu

Misalnya, dalam menyelesaikan soal tentang persamaan garis lurus y = 2x + 3, alat bantu dapat digunakan untuk:

• Menghitung titik potong sumbu x dan y dengan kalkulator.
• Membuat grafik persamaan garis lurus dengan software matematika seperti GeoGebra.
• Menganalisis hubungan antara nilai x dan y dengan aplikasi grafis seperti Microsoft Excel.

Manfaat dan Kelemahan Penggunaan Alat Bantu

Penggunaan alat bantu dalam analisis grafik persamaan garis lurus memiliki beberapa manfaat, antara lain:

• Meningkatkan keakuratan perhitungan dan visualisasi grafik.
• Mempercepat proses analisis dan penyelesaian masalah.
• Mempermudah pemahaman konsep dan hubungan antara persamaan garis lurus dengan grafiknya.

Namun, penggunaan alat bantu juga memiliki beberapa kelemahan, seperti:

• Ketergantungan pada alat bantu dapat mengurangi kemampuan analisis manual.
• Tidak semua alat bantu mudah diakses atau dipelajari.
• Terkadang alat bantu dapat memberikan hasil yang salah jika digunakan secara tidak tepat.

Pengembangan Kreativitas dalam Menyelesaikan Soal Grafik Persamaan Garis Lurus

Memecahkan soal grafik persamaan garis lurus tidak melulu tentang menghafal rumus dan prosedur. Kreativitas berperan penting dalam menemukan solusi yang efisien dan mendalam, bahkan untuk soal-soal yang tampak rumit. Kreativitas dalam konteks ini bukan berarti menemukan jawaban yang tidak konvensional, melainkan kemampuan untuk melihat masalah dari berbagai sudut pandang, menemukan pola, dan menerapkan strategi yang unik.

Bagaimana Kreativitas Membantu dalam Menyelesaikan Soal Grafik Persamaan Garis Lurus?

Kreativitas dapat membantu dalam menyelesaikan soal grafik persamaan garis lurus dengan beberapa cara:

• Melihat pola dan hubungan: Kreativitas memungkinkan kita untuk melihat pola dan hubungan tersembunyi dalam data dan grafik. Misalnya, dengan melihat pola titik-titik yang diberikan, kita dapat menebak bentuk garis lurus yang menghubungkan titik-titik tersebut.
• Menemukan solusi alternatif: Kreativitas membuka pintu bagi kita untuk menemukan solusi alternatif selain metode standar. Misalnya, dalam menentukan persamaan garis lurus, kita bisa menggunakan metode gradien-titik atau persamaan garis lurus umum, tergantung pada informasi yang diberikan.
• Meningkatkan pemahaman konsep: Kreativitas mendorong kita untuk memahami konsep di balik rumus dan prosedur. Dengan berpikir kreatif, kita dapat memahami mengapa rumus tertentu bekerja dan bagaimana menerapkannya dalam berbagai situasi.

Strategi Kreatif untuk Menyelesaikan Soal Grafik Persamaan Garis Lurus

Berikut adalah beberapa strategi kreatif yang dapat digunakan dalam menyelesaikan soal grafik persamaan garis lurus:

• Visualisasi: Gambarlah grafik persamaan garis lurus dan titik-titik yang diberikan. Visualisasi membantu dalam memahami hubungan antara data dan persamaan.
• Mencoba berbagai metode: Jangan takut untuk mencoba berbagai metode untuk menyelesaikan masalah. Misalnya, jika metode gradien-titik tidak berhasil, cobalah menggunakan persamaan garis lurus umum.
• Mencari pola: Perhatikan pola dalam data dan grafik. Apakah titik-titik membentuk pola tertentu? Apakah ada hubungan antara titik-titik dan persamaan garis lurus?
• Membuat tabel: Buat tabel untuk mencatat data dan hasil perhitungan. Tabel membantu dalam mengorganisir informasi dan melihat pola.
• Berdiskusi dengan teman: Diskusikan soal dengan teman dan bagikan ide-ide kreatif. Mendengar perspektif orang lain dapat membuka jalan baru dalam menyelesaikan masalah.

Manfaat Kreativitas dalam Menemukan Solusi Alternatif dan Meningkatkan Pemahaman Konsep

Kreativitas dalam menyelesaikan soal grafik persamaan garis lurus tidak hanya membantu menemukan solusi alternatif, tetapi juga meningkatkan pemahaman konsep. Dengan mencoba berbagai metode dan melihat masalah dari berbagai sudut pandang, kita dapat memahami konsep di balik rumus dan prosedur dengan lebih baik. Misalnya, dengan mencoba menyelesaikan soal dengan berbagai metode, kita dapat memahami bagaimana masing-masing metode bekerja dan kapan metode tersebut paling efektif.

Kreativitas juga dapat membantu dalam menemukan solusi yang lebih efisien dan elegan. Dengan berpikir kreatif, kita dapat menemukan cara-cara baru untuk menyelesaikan masalah yang tidak hanya benar, tetapi juga mudah dipahami dan diimplementasikan.

Menghubungkan Grafik Persamaan Garis Lurus dengan Dunia Kerja

Konsep grafik persamaan garis lurus mungkin tampak sederhana, tetapi aplikasinya meluas dan sangat penting dalam berbagai bidang pekerjaan. Grafik ini mampu menggambarkan hubungan antara dua variabel, sehingga dapat membantu dalam menganalisis data, membuat prediksi, dan membuat keputusan yang tepat.

Penerapan Grafik Persamaan Garis Lurus dalam Dunia Kerja

Grafik persamaan garis lurus memiliki peran penting dalam berbagai bidang pekerjaan, seperti ekonomi, teknik, dan bisnis.

• Ekonomi: Grafik persamaan garis lurus digunakan untuk menggambarkan hubungan antara variabel ekonomi seperti permintaan dan penawaran, harga dan kuantitas, atau inflasi dan pengangguran. Misalnya, grafik permintaan dapat menunjukkan hubungan antara harga suatu produk dan jumlah produk yang diminta oleh konsumen. Dengan memahami hubungan ini, ekonom dapat membuat prediksi tentang perubahan harga dan kuantitas, serta menganalisis dampak kebijakan ekonomi.
• Teknik: Grafik persamaan garis lurus digunakan untuk menggambarkan hubungan antara variabel teknik seperti kecepatan dan waktu, gaya dan perpindahan, atau tegangan dan arus. Misalnya, grafik kecepatan dan waktu dapat digunakan untuk menghitung jarak yang ditempuh oleh suatu objek. Dengan memahami hubungan ini, insinyur dapat mendesain sistem dan komponen yang lebih efisien dan efektif.
• Bisnis: Grafik persamaan garis lurus digunakan untuk menggambarkan hubungan antara variabel bisnis seperti penjualan dan biaya, keuntungan dan kerugian, atau produksi dan konsumsi. Misalnya, grafik penjualan dapat menunjukkan hubungan antara jumlah produk yang terjual dan pendapatan yang dihasilkan. Dengan memahami hubungan ini, manajer dapat membuat prediksi tentang penjualan dan keuntungan, serta membuat keputusan tentang strategi pemasaran dan produksi.

Contoh Kasus Nyata di Dunia Kerja

Berikut beberapa contoh kasus nyata di dunia kerja yang melibatkan aplikasi grafik persamaan garis lurus:

• Analisis Tren Penjualan: Seorang manajer pemasaran menggunakan grafik persamaan garis lurus untuk menganalisis tren penjualan produk baru. Dengan menghubungkan data penjualan selama beberapa bulan, dia dapat melihat pola penjualan dan memprediksi penjualan di masa depan. Informasi ini membantu dalam menentukan strategi pemasaran yang efektif untuk meningkatkan penjualan.
• Perencanaan Produksi: Seorang manajer produksi menggunakan grafik persamaan garis lurus untuk merencanakan produksi berdasarkan permintaan pasar. Dengan menghubungkan data permintaan dengan kapasitas produksi, dia dapat menentukan jumlah produk yang harus diproduksi setiap bulan untuk memenuhi permintaan dan meminimalkan biaya produksi.
• Analisis Biaya: Seorang akuntan menggunakan grafik persamaan garis lurus untuk menganalisis biaya produksi. Dengan menghubungkan data biaya dengan volume produksi, dia dapat mengidentifikasi biaya tetap dan biaya variabel, serta memprediksi total biaya produksi untuk berbagai tingkat produksi.

Manfaat Pemahaman Grafik Persamaan Garis Lurus di Dunia Kerja

Memahami konsep grafik persamaan garis lurus dapat memberikan berbagai manfaat dalam dunia kerja:

• Analisis Data: Grafik persamaan garis lurus membantu dalam menganalisis data dan mengidentifikasi pola dan tren yang penting. Dengan memahami hubungan antara variabel, Anda dapat membuat prediksi yang lebih akurat dan membuat keputusan yang lebih tepat.
• Pemecahan Masalah: Grafik persamaan garis lurus dapat membantu dalam memecahkan masalah yang melibatkan dua variabel. Dengan menggambarkan hubungan antara variabel, Anda dapat menemukan solusi yang optimal dan efektif.
• Komunikasi yang Lebih Efektif: Grafik persamaan garis lurus merupakan alat komunikasi yang efektif untuk menyampaikan informasi kompleks kepada audiens yang lebih luas. Dengan visualisasi data, Anda dapat membuat presentasi yang lebih menarik dan mudah dipahami.

Kesimpulan Akhir

Dengan memahami konsep persamaan garis lurus, Anda akan memiliki alat yang ampuh untuk menganalisis data, menyelesaikan masalah, dan membuat keputusan yang lebih baik. Mari kita mulai perjalanan ini dan temukan keajaiban garis lurus!