Contoh soal himpunan matematika kuliah – Bersiaplah untuk menjelajahi dunia himpunan dalam matematika kuliah! Himpunan, konsep dasar dalam matematika, memiliki peran penting dalam berbagai bidang, mulai dari ilmu komputer hingga ekonomi. Melalui contoh soal yang menarik, kita akan mengasah pemahaman tentang operasi himpunan, kardinalitas, himpunan bagian, dan himpunan kuasa. Siap untuk menguji kemampuanmu dalam menguasai konsep-konsep ini?
Dalam contoh soal ini, kita akan mempelajari berbagai jenis himpunan, seperti himpunan kosong, himpunan berhingga, dan himpunan tak berhingga. Selain itu, kita akan memahami operasi dasar himpunan, seperti irisan, gabungan, selisih, dan komplemen. Contoh soal ini akan memperjelas bagaimana konsep himpunan diterapkan dalam berbagai bidang, sehingga kamu dapat memahami aplikasi praktisnya dalam kehidupan sehari-hari.
Pengertian Himpunan
Himpunan merupakan konsep dasar dalam matematika yang sangat penting untuk memahami konsep matematika lainnya. Himpunan adalah kumpulan objek yang memiliki ciri atau sifat tertentu. Objek-objek tersebut disebut anggota atau elemen dari himpunan. Himpunan dapat berupa kumpulan benda nyata, seperti kumpulan buah-buahan, atau kumpulan abstrak, seperti kumpulan bilangan prima.
Contoh Himpunan dan Bukan Himpunan
Berikut ini beberapa contoh himpunan dan bukan himpunan:
- Himpunan:
- Kumpulan bilangan genap antara 1 dan 10: 2, 4, 6, 8
- Kumpulan huruf vokal dalam alfabet: a, i, u, e, o
- Kumpulan negara di Asia Tenggara: Indonesia, Malaysia, Singapura, Thailand, Filipina, Vietnam, Myanmar, Laos, Brunei Darussalam, Timor Leste
- Bukan Himpunan:
- Kumpulan orang yang tinggi
- Kumpulan makanan yang enak
- Kumpulan hewan yang lucu
Perhatikan bahwa kumpulan orang yang tinggi, makanan yang enak, dan hewan yang lucu tidak dapat disebut himpunan karena tidak memiliki ciri atau sifat yang jelas dan terdefinisi. Tinggi, enak, dan lucu merupakan konsep yang subjektif dan relatif, sehingga tidak dapat dijadikan dasar untuk menentukan anggota dari suatu himpunan.
Jenis-jenis Himpunan
Himpunan dapat diklasifikasikan menjadi beberapa jenis berdasarkan ciri atau sifat anggotanya. Berikut adalah tabel yang membandingkan jenis-jenis himpunan dengan contohnya masing-masing:
| Jenis Himpunan | Contoh |
|---|---|
| Himpunan kosong | Himpunan yang tidak memiliki anggota, dilambangkan dengan atau ∅. Contoh: Himpunan bilangan bulat yang lebih besar dari 10 dan lebih kecil dari 5. |
| Himpunan berhingga | Himpunan yang memiliki jumlah anggota yang terbatas. Contoh: Himpunan bilangan bulat positif kurang dari 10: 1, 2, 3, 4, 5, 6, 7, 8, 9. |
| Himpunan tak berhingga | Himpunan yang memiliki jumlah anggota yang tak terbatas. Contoh: Himpunan bilangan bulat: …, -3, -2, -1, 0, 1, 2, 3, …. |
| Himpunan bagian | Himpunan yang semua anggotanya juga merupakan anggota dari himpunan lain. Contoh: Himpunan 2, 4, 6 adalah himpunan bagian dari himpunan 1, 2, 3, 4, 5, 6. |
| Himpunan semesta | Himpunan yang memuat semua anggota yang sedang dibicarakan dalam suatu pembahasan. Contoh: Himpunan bilangan bulat: …, -3, -2, -1, 0, 1, 2, 3, …. |
Operasi Himpunan
Setelah memahami konsep himpunan, kita akan membahas operasi-operasi dasar yang dapat dilakukan pada himpunan. Operasi himpunan ini memungkinkan kita untuk menggabungkan, memisahkan, atau mencari elemen yang sama di antara himpunan. Operasi-operasi ini sangat penting dalam berbagai bidang matematika, seperti teori peluang, statistika, dan aljabar.
Irisan Himpunan
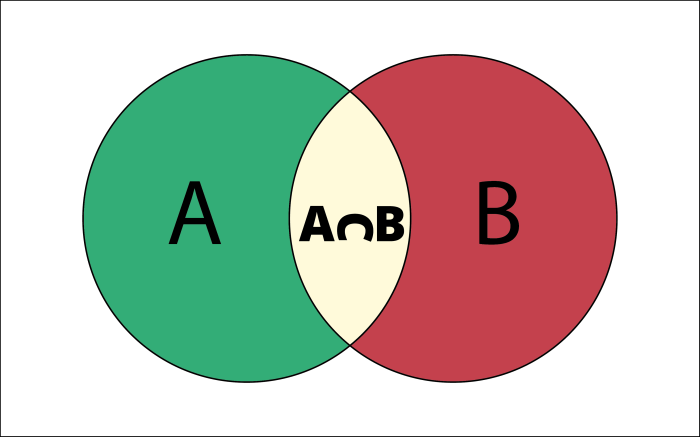
Irisan himpunan adalah operasi yang menghasilkan himpunan baru yang berisi elemen-elemen yang terdapat di kedua himpunan. Irisan dari dua himpunan A dan B dilambangkan dengan A ∩ B.
- Secara formal, A ∩ B = x | x ∈ A dan x ∈ B.
- Contoh: Jika A = 1, 2, 3, 4 dan B = 3, 4, 5, 6, maka A ∩ B = 3, 4.
- Diagram Venn: Irisan himpunan dapat digambarkan dengan diagram Venn, yaitu dua lingkaran yang saling tumpang tindih. Bagian yang tumpang tindih mewakili irisan dari kedua himpunan.
Gabungan Himpunan
Gabungan himpunan adalah operasi yang menghasilkan himpunan baru yang berisi semua elemen dari kedua himpunan. Gabungan dari dua himpunan A dan B dilambangkan dengan A ∪ B.
- Secara formal, A ∪ B = x | x ∈ A atau x ∈ B.
- Contoh: Jika A = 1, 2, 3, 4 dan B = 3, 4, 5, 6, maka A ∪ B = 1, 2, 3, 4, 5, 6.
- Diagram Venn: Gabungan himpunan dapat digambarkan dengan diagram Venn, yaitu dua lingkaran yang saling tumpang tindih. Bagian yang dipenuhi oleh kedua lingkaran mewakili gabungan dari kedua himpunan.
Selisih Himpunan
Selisih himpunan adalah operasi yang menghasilkan himpunan baru yang berisi elemen-elemen yang terdapat di himpunan pertama tetapi tidak terdapat di himpunan kedua. Selisih dari dua himpunan A dan B dilambangkan dengan A – B.
- Secara formal, A – B = x | x ∈ A dan x ∉ B.
- Contoh: Jika A = 1, 2, 3, 4 dan B = 3, 4, 5, 6, maka A – B = 1, 2.
- Diagram Venn: Selisih himpunan dapat digambarkan dengan diagram Venn, yaitu dua lingkaran yang saling tumpang tindih. Bagian dari lingkaran pertama yang tidak tumpang tindih dengan lingkaran kedua mewakili selisih dari kedua himpunan.
Komplemen Himpunan
Komplemen himpunan adalah operasi yang menghasilkan himpunan baru yang berisi semua elemen yang tidak terdapat di himpunan tersebut. Komplemen dari himpunan A dilambangkan dengan A’.
- Secara formal, A’ = x | x ∉ A.
- Contoh: Jika A = 1, 2, 3, 4 dan S = 1, 2, 3, 4, 5, 6 (S adalah himpunan semesta), maka A’ = 5, 6.
- Diagram Venn: Komplemen himpunan dapat digambarkan dengan diagram Venn, yaitu satu lingkaran yang mewakili himpunan A dan bagian di luar lingkaran tersebut mewakili komplemen dari himpunan A.
Kardinalitas Himpunan
Dalam dunia matematika, kardinalitas himpunan adalah konsep penting yang merujuk pada jumlah elemen dalam suatu himpunan. Konsep ini membantu kita memahami “ukuran” suatu himpunan dan membandingkannya dengan himpunan lainnya.
Pengertian Kardinalitas Himpunan
Kardinalitas himpunan adalah ukuran yang menunjukkan berapa banyak elemen yang terkandung dalam himpunan tersebut. Secara sederhana, kardinalitas menyatakan jumlah anggota dalam suatu himpunan.
Contoh Soal Menentukan Kardinalitas Himpunan
Misalkan kita memiliki himpunan A = 1, 2, 3, 4, 5. Kardinalitas himpunan A, yang dinotasikan sebagai |A|, adalah 5. Ini karena himpunan A memiliki 5 elemen.
Kardinalitas Himpunan Kosong, Berhingga, dan Tak Berhingga
Kardinalitas himpunan dapat dibedakan menjadi tiga jenis berdasarkan jumlah elemennya:
| Jenis Himpunan | Kardinalitas | Contoh |
|---|---|---|
| Himpunan Kosong | 0 | |
| Himpunan Berhingga | Bilangan bulat positif | a, b, c, 1, 2, 3, 4, 5 |
| Himpunan Tak Berhingga | ∞ | Himpunan bilangan bulat, himpunan bilangan real |
Himpunan Bagian: Contoh Soal Himpunan Matematika Kuliah
Himpunan bagian merupakan konsep penting dalam teori himpunan. Konsep ini menjelaskan hubungan antara dua himpunan, yaitu himpunan induk (himpunan yang lebih besar) dan himpunan bagian (himpunan yang lebih kecil). Dalam pembahasan ini, kita akan membahas pengertian himpunan bagian, contoh soal, dan langkah-langkah untuk menentukan himpunan bagian dari suatu himpunan.
Pengertian Himpunan Bagian
Himpunan bagian adalah himpunan yang semua anggotanya juga merupakan anggota dari himpunan lain yang lebih besar. Himpunan yang lebih besar ini disebut sebagai himpunan induk.
Contoh Soal Menentukan Himpunan Bagian
Misalkan kita memiliki himpunan A = 1, 2, 3 dan himpunan B = 1, 2. Himpunan B merupakan himpunan bagian dari himpunan A karena semua anggota B (1 dan 2) juga merupakan anggota A.
Langkah-Langkah Menentukan Himpunan Bagian
Berikut langkah-langkah untuk menentukan himpunan bagian dari suatu himpunan:
- Tentukan semua kemungkinan kombinasi anggota dari himpunan induk.
- Pilih kombinasi yang semua anggotanya juga merupakan anggota dari himpunan induk.
- Himpunan yang dipilih adalah himpunan bagian dari himpunan induk.
Himpunan Kuasa
Himpunan kuasa adalah konsep penting dalam teori himpunan. Ini adalah himpunan yang berisi semua himpunan bagian dari suatu himpunan. Dengan kata lain, himpunan kuasa adalah himpunan dari semua kemungkinan cara untuk memilih elemen dari himpunan asal, termasuk himpunan kosong dan himpunan asal itu sendiri.
Menentukan Himpunan Kuasa
Untuk menentukan himpunan kuasa dari suatu himpunan, kita perlu mempertimbangkan semua kemungkinan kombinasi elemen dalam himpunan tersebut. Berikut adalah langkah-langkah yang dapat digunakan untuk menentukan himpunan kuasa:
- Tentukan jumlah elemen dalam himpunan asal. Misalnya, jika himpunan asal memiliki 3 elemen, maka himpunan kuasanya akan memiliki 23 = 8 elemen.
- Buatlah daftar semua kemungkinan kombinasi elemen, mulai dari himpunan kosong hingga himpunan asal itu sendiri. Setiap kombinasi merupakan himpunan bagian dari himpunan asal.
- Himpunan kuasa adalah himpunan yang berisi semua kombinasi elemen yang telah Anda buat.
Contoh Soal
Misalkan kita memiliki himpunan A = a, b, c. Himpunan kuasa dari A, yang dilambangkan dengan P(A), adalah:
P(A) = , a, b, c, a, b, a, c, b, c, a, b, c
Himpunan kuasa P(A) berisi 8 elemen, yang merupakan semua himpunan bagian dari A, termasuk himpunan kosong dan himpunan A itu sendiri.
Aplikasi Himpunan
Konsep himpunan memiliki aplikasi yang luas dan mendalam dalam berbagai bidang kehidupan, mulai dari yang sederhana hingga yang kompleks. Pemahaman tentang himpunan memungkinkan kita untuk mengelompokkan, mengklasifikasikan, dan menganalisis informasi dengan lebih terstruktur.
Aplikasi Himpunan dalam Kehidupan Sehari-hari, Contoh soal himpunan matematika kuliah
Konsep himpunan sering kita gunakan dalam kehidupan sehari-hari tanpa kita sadari. Sebagai contoh, saat kita pergi ke supermarket, kita akan memilih barang-barang yang kita butuhkan dan memasukkannya ke dalam keranjang. Keranjang ini dapat dianalogikan sebagai himpunan, dan barang-barang yang kita pilih merupakan anggota dari himpunan tersebut. Contoh lainnya, saat kita ingin membuat daftar belanja, kita akan menuliskan semua barang yang ingin kita beli. Daftar belanja ini juga dapat dianggap sebagai himpunan, dan barang-barang yang kita tulis merupakan anggota dari himpunan tersebut.
Aplikasi Himpunan dalam Komputer
Dalam ilmu komputer, konsep himpunan digunakan dalam berbagai aspek, seperti dalam pemrograman, database, dan algoritma.
- Dalam pemrograman, himpunan digunakan untuk menyimpan dan mengelola data yang unik. Contohnya, dalam bahasa pemrograman Python, kita dapat menggunakan tipe data
setuntuk menyimpan kumpulan data yang tidak berulang. - Dalam database, himpunan digunakan untuk mengelola data yang unik dan terstruktur. Contohnya, dalam sistem manajemen database relasional (RDBMS), kita dapat menggunakan tabel untuk menyimpan data yang terorganisir dalam bentuk baris dan kolom, dan setiap kolom dapat dianggap sebagai himpunan data.
- Dalam algoritma, himpunan digunakan untuk mengoptimalkan proses pencarian dan pengurutan data. Contohnya, algoritma pencarian set (set search algorithm) digunakan untuk mencari elemen yang unik dalam himpunan data.
Aplikasi Himpunan dalam Statistik
Dalam statistik, konsep himpunan digunakan untuk mengklasifikasikan dan menganalisis data.
- Contohnya, dalam analisis data demografi, kita dapat menggunakan himpunan untuk mengelompokkan populasi berdasarkan karakteristik tertentu, seperti usia, jenis kelamin, dan pendidikan.
- Himpunan juga digunakan dalam analisis data kualitatif, seperti dalam penelitian sosial, untuk mengelompokkan data berdasarkan tema dan kategori.
Aplikasi Himpunan dalam Ekonomi
Dalam ekonomi, konsep himpunan digunakan untuk menganalisis perilaku konsumen dan produsen.
- Contohnya, dalam teori permintaan, kita dapat menggunakan himpunan untuk menggambarkan preferensi konsumen terhadap berbagai barang dan jasa.
- Himpunan juga digunakan dalam teori produksi untuk menganalisis kombinasi faktor produksi yang optimal untuk menghasilkan output tertentu.
Ilustrasi Aplikasi Himpunan dalam Bidang Ekonomi
Misalnya, dalam analisis pasar, kita dapat menggunakan himpunan untuk menggambarkan preferensi konsumen terhadap berbagai produk.
- Misalkan, kita ingin menganalisis preferensi konsumen terhadap minuman ringan. Kita dapat mengelompokkan konsumen berdasarkan jenis minuman ringan yang mereka sukai, seperti minuman bersoda, minuman jus, atau minuman tanpa gula.
- Dengan menggunakan himpunan, kita dapat mengidentifikasi segmen pasar yang berbeda dan mengembangkan strategi pemasaran yang tepat untuk setiap segmen.
Ringkasan Penutup
Melalui contoh soal yang telah dibahas, diharapkan kamu semakin memahami konsep himpunan dan berbagai operasinya. Jangan lupa untuk berlatih mengerjakan soal-soal lain untuk mengasah kemampuanmu. Selamat belajar dan semoga sukses dalam memahami dunia himpunan!





