Contoh soal histogram poligon frekuensi dan ogive – Pernahkah kamu melihat diagram batang yang unik, atau garis yang menggambarkan data dengan jelas? Itulah histogram, poligon frekuensi, dan ogive! Ketiga jenis diagram ini merupakan alat bantu visual yang powerful untuk memahami data secara mudah dan menarik. Bayangkan, kamu bisa melihat langsung pola dan tren dalam data tanpa harus membaca angka-angka yang rumit.
Dalam artikel ini, kita akan menjelajahi dunia histogram, poligon frekuensi, dan ogive dengan lebih dalam. Kita akan belajar bagaimana membuat diagram-diagram ini, memahami perbedaannya, dan bahkan melihat bagaimana mereka diterapkan dalam kehidupan sehari-hari. Siap-siap untuk menyelami dunia data yang menarik!
Pengertian Histogram, Poligon Frekuensi, dan Ogive
Dalam dunia statistika, data yang dikumpulkan perlu disajikan dalam bentuk yang mudah dipahami dan diinterpretasikan. Histogram, poligon frekuensi, dan ogive adalah tiga jenis diagram yang digunakan untuk menyajikan data secara visual, membantu kita melihat pola dan tren dalam data yang dikumpulkan.
Histogram
Histogram adalah diagram yang menampilkan distribusi frekuensi data dalam bentuk batang-batang. Setiap batang mewakili kelas interval data, dengan tinggi batang menunjukkan frekuensi data dalam kelas interval tersebut. Batang-batang dalam histogram berdampingan tanpa celah, menunjukkan kontinuitas data dalam kelas interval.
Sebagai contoh, jika kita ingin melihat distribusi usia siswa di sebuah kelas, kita dapat membuat histogram dengan kelas interval 5 tahun (misalnya, 15-19 tahun, 20-24 tahun, dan seterusnya). Tinggi batang akan menunjukkan jumlah siswa dalam setiap kelas interval.
Poligon Frekuensi
Poligon frekuensi adalah diagram garis yang menunjukkan distribusi frekuensi data. Titik-titik pada diagram mewakili titik tengah kelas interval data, dengan tinggi titik menunjukkan frekuensi data dalam kelas interval tersebut. Titik-titik dihubungkan dengan garis lurus, membentuk poligon.
Contohnya, dengan data usia siswa yang sama, poligon frekuensi akan menampilkan titik-titik yang mewakili titik tengah kelas interval (misalnya, 17 tahun untuk kelas interval 15-19 tahun, 22 tahun untuk kelas interval 20-24 tahun, dan seterusnya). Titik-titik tersebut dihubungkan dengan garis lurus, membentuk poligon yang menunjukkan distribusi usia siswa.
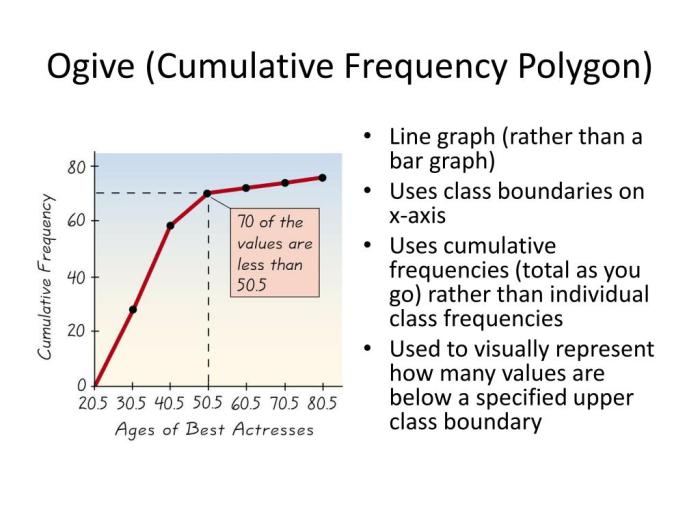
Ogive
Ogive adalah diagram garis kumulatif yang menunjukkan frekuensi kumulatif data. Titik-titik pada diagram mewakili batas atas kelas interval data, dengan tinggi titik menunjukkan frekuensi kumulatif data hingga batas atas kelas interval tersebut. Titik-titik dihubungkan dengan garis lurus, membentuk ogive.
Contohnya, dengan data usia siswa yang sama, ogive akan menampilkan titik-titik yang mewakili batas atas kelas interval (misalnya, 19 tahun untuk kelas interval 15-19 tahun, 24 tahun untuk kelas interval 20-24 tahun, dan seterusnya). Tinggi titik akan menunjukkan jumlah total siswa yang berusia 19 tahun atau kurang, 24 tahun atau kurang, dan seterusnya. Titik-titik tersebut dihubungkan dengan garis lurus, membentuk ogive yang menunjukkan frekuensi kumulatif usia siswa.
Perbedaan Histogram, Poligon Frekuensi, dan Ogive, Contoh soal histogram poligon frekuensi dan ogive
| Fitur | Histogram | Poligon Frekuensi | Ogive |
|---|---|---|---|
| Bentuk | Batang | Garis | Garis |
| Data yang Ditampilkan | Frekuensi data | Frekuensi data | Frekuensi kumulatif data |
| Hubungan Antar Batang/Titik | Berdampingan | Titik dihubungkan dengan garis | Titik dihubungkan dengan garis |
| Kegunaan | Menampilkan distribusi frekuensi data | Menampilkan distribusi frekuensi data | Menampilkan frekuensi kumulatif data |
Langkah-Langkah Membuat Histogram
Histogram adalah representasi grafis dari distribusi data yang menunjukkan frekuensi data dalam rentang kelas tertentu. Histogram berguna untuk memahami pola dan tren dalam kumpulan data.
Langkah-Langkah Membuat Histogram
Berikut adalah langkah-langkah untuk membuat histogram:
- Kumpulkan data dan tentukan rentang data.
- Tentukan jumlah kelas yang akan digunakan. Jumlah kelas yang ideal dapat ditentukan dengan menggunakan aturan Sturges, yaitu 1 + 3.322 * log(n), di mana n adalah jumlah data.
- Hitung lebar kelas dengan membagi rentang data dengan jumlah kelas.
- Buat tabel frekuensi yang menunjukkan frekuensi data dalam setiap kelas.
- Gambarlah sumbu horizontal (sumbu x) dan sumbu vertikal (sumbu y). Sumbu x mewakili kelas, sedangkan sumbu y mewakili frekuensi.
- Buatlah persegi panjang untuk setiap kelas dengan lebar yang sama dengan lebar kelas dan tinggi yang sama dengan frekuensi kelas tersebut.
- Persegi panjang-persegi panjang tersebut harus berdampingan tanpa celah di antara mereka.
Contoh Soal
Misalnya, kita memiliki data berikut tentang tinggi badan 10 siswa (dalam cm): 150, 155, 160, 165, 170, 175, 180, 185, 190, 195.
- Rentang data adalah 195 – 150 = 45 cm.
- Jumlah kelas yang ideal dapat ditentukan dengan menggunakan aturan Sturges: 1 + 3.322 * log(10) ≈ 4 kelas.
- Lebar kelas adalah 45 cm / 4 kelas = 11.25 cm. Kita dapat membulatkan lebar kelas menjadi 12 cm untuk memudahkan perhitungan.
Berikut tabel frekuensi yang menunjukkan frekuensi data dalam setiap kelas:
| Kelas | Frekuensi |
|---|---|
| 150-162 | 3 |
| 163-175 | 4 |
| 176-188 | 2 |
| 189-201 | 1 |
Frekuensi Kumulatif dan Frekuensi Relatif
Berikut adalah tabel yang menunjukkan frekuensi kumulatif dan frekuensi relatif dari data contoh:
| Kelas | Frekuensi | Frekuensi Kumulatif | Frekuensi Relatif |
|---|---|---|---|
| 150-162 | 3 | 3 | 0.3 |
| 163-175 | 4 | 7 | 0.4 |
| 176-188 | 2 | 9 | 0.2 |
| 189-201 | 1 | 10 | 0.1 |
Ilustrasi Histogram
Berikut ilustrasi histogram dari data contoh:
[Gambar histogram yang menunjukkan distribusi frekuensi data tinggi badan siswa dalam setiap kelas]
Histogram menunjukkan bahwa sebagian besar siswa memiliki tinggi badan antara 163 cm hingga 175 cm.
Langkah-Langkah Membuat Poligon Frekuensi
Poligon frekuensi adalah representasi grafis dari distribusi data yang menunjukkan frekuensi setiap kelas data dengan menghubungkan titik tengah setiap kelas dengan garis lurus. Pembuatan poligon frekuensi merupakan langkah penting dalam analisis data, terutama untuk memahami pola distribusi data dan membandingkan data dari berbagai sumber.
Langkah-Langkah Membuat Poligon Frekuensi
Berikut adalah langkah-langkah untuk membuat poligon frekuensi:
- Buat tabel frekuensi. Tabel frekuensi menunjukkan jumlah data dalam setiap kelas.
- Tentukan titik tengah setiap kelas. Titik tengah kelas dihitung dengan menjumlahkan batas bawah dan batas atas kelas kemudian dibagi dua.
- Plot titik-titik pada grafik. Titik-titik diplot dengan titik tengah kelas pada sumbu x dan frekuensi pada sumbu y.
- Hubungkan titik-titik dengan garis lurus. Garis lurus yang menghubungkan titik-titik membentuk poligon frekuensi.
- Berikan label pada sumbu x dan sumbu y. Label sumbu x menunjukkan kelas data, sedangkan label sumbu y menunjukkan frekuensi.
- Berikan judul pada grafik. Judul grafik harus menggambarkan data yang digambarkan.
Contoh Soal
Berikut adalah contoh soal untuk menggambarkan langkah-langkah pembuatan poligon frekuensi:
Misalkan terdapat data nilai ujian 10 siswa sebagai berikut: 70, 80, 75, 85, 90, 75, 80, 85, 90, 75.
Langkah-langkah pembuatan poligon frekuensi untuk data tersebut adalah:
- Buat tabel frekuensi. Tabel frekuensi menunjukkan jumlah data dalam setiap kelas. Misalkan kelas data yang digunakan adalah 70-75, 75-80, 80-85, 85-90, dan 90-95.
- Tentukan titik tengah setiap kelas. Titik tengah kelas dihitung dengan menjumlahkan batas bawah dan batas atas kelas kemudian dibagi dua.
| Kelas | Frekuensi | Titik Tengah |
|---|---|---|
| 70-75 | 3 | 72.5 |
| 75-80 | 2 | 77.5 |
| 80-85 | 2 | 82.5 |
| 85-90 | 2 | 87.5 |
| 90-95 | 1 | 92.5 |
Setelah membuat tabel frekuensi, langkah selanjutnya adalah memplot titik-titik pada grafik dengan titik tengah kelas pada sumbu x dan frekuensi pada sumbu y. Kemudian, hubungkan titik-titik dengan garis lurus untuk membentuk poligon frekuensi.
Berikut adalah ilustrasi poligon frekuensi dari data nilai ujian 10 siswa:
[Gambar Poligon Frekuensi]
Gambar tersebut menunjukkan bahwa kelas data dengan frekuensi tertinggi adalah kelas 70-75, sedangkan kelas data dengan frekuensi terendah adalah kelas 90-95.
Tabel Frekuensi Kumulatif dan Frekuensi Relatif
Selain tabel frekuensi, kita juga dapat membuat tabel frekuensi kumulatif dan frekuensi relatif. Tabel frekuensi kumulatif menunjukkan jumlah data yang kurang dari atau sama dengan batas atas kelas tertentu. Sedangkan tabel frekuensi relatif menunjukkan proporsi data dalam setiap kelas.
| Kelas | Frekuensi | Frekuensi Kumulatif | Frekuensi Relatif |
|---|---|---|---|
| 70-75 | 3 | 3 | 0.3 |
| 75-80 | 2 | 5 | 0.2 |
| 80-85 | 2 | 7 | 0.2 |
| 85-90 | 2 | 9 | 0.2 |
| 90-95 | 1 | 10 | 0.1 |
Tabel di atas menunjukkan bahwa frekuensi kumulatif untuk kelas 75-80 adalah 5, artinya ada 5 siswa yang memiliki nilai ujian kurang dari atau sama dengan 80. Frekuensi relatif untuk kelas 70-75 adalah 0.3, artinya 30% dari siswa memiliki nilai ujian dalam kelas 70-75.
Langkah-Langkah Membuat Ogive
Ogive merupakan kurva yang menggambarkan distribusi kumulatif frekuensi data. Ogive digunakan untuk mengetahui persentase data yang berada di bawah suatu nilai tertentu. Dalam pembuatan ogive, kita perlu menghitung frekuensi kumulatif dan frekuensi relatif dari data yang tersedia.
Langkah-Langkah Membuat Ogive
Berikut adalah langkah-langkah membuat ogive:
- Tentukan kelas interval dan frekuensi masing-masing kelas interval.
- Hitung frekuensi kumulatif. Frekuensi kumulatif adalah jumlah frekuensi dari kelas interval tertentu dan kelas interval sebelumnya.
- Hitung frekuensi relatif. Frekuensi relatif adalah perbandingan frekuensi kumulatif dengan jumlah total data.
- Buat tabel yang menunjukkan frekuensi kumulatif dan frekuensi relatif.
- Plot titik-titik pada grafik. Titik-titik tersebut adalah titik tengah kelas interval di sumbu x dan frekuensi kumulatif di sumbu y.
- Hubungkan titik-titik tersebut dengan garis lurus. Garis yang dihasilkan adalah ogive.
Contoh Soal
Berikut adalah contoh soal untuk membuat ogive:
Misalnya, terdapat data nilai ujian 20 siswa sebagai berikut:
| Nilai | Frekuensi |
|---|---|
| 60-69 | 2 |
| 70-79 | 5 |
| 80-89 | 8 |
| 90-99 | 5 |
Langkah-langkah pembuatan ogive untuk data tersebut adalah sebagai berikut:
- Tentukan kelas interval dan frekuensi masing-masing kelas interval. Dalam contoh ini, kelas interval sudah ditentukan dan frekuensi masing-masing kelas interval sudah diketahui.
- Hitung frekuensi kumulatif. Frekuensi kumulatif dihitung dengan menjumlahkan frekuensi kelas interval tertentu dengan frekuensi kelas interval sebelumnya. Berikut tabel frekuensi kumulatif dari data contoh:
- Hitung frekuensi relatif. Frekuensi relatif dihitung dengan membagi frekuensi kumulatif dengan jumlah total data. Berikut tabel frekuensi relatif dari data contoh:
- Buat tabel yang menunjukkan frekuensi kumulatif dan frekuensi relatif. Tabel tersebut sudah dibuat pada langkah sebelumnya.
- Plot titik-titik pada grafik. Titik-titik tersebut adalah titik tengah kelas interval di sumbu x dan frekuensi kumulatif di sumbu y. Berikut adalah contoh grafik ogive:
- Hubungkan titik-titik tersebut dengan garis lurus. Garis yang dihasilkan adalah ogive. Langkah ini sudah dilakukan pada langkah sebelumnya.
| Nilai | Frekuensi | Frekuensi Kumulatif |
|---|---|---|
| 60-69 | 2 | 2 |
| 70-79 | 5 | 7 |
| 80-89 | 8 | 15 |
| 90-99 | 5 | 20 |
| Nilai | Frekuensi | Frekuensi Kumulatif | Frekuensi Relatif |
|---|---|---|---|
| 60-69 | 2 | 2 | 0,1 |
| 70-79 | 5 | 7 | 0,35 |
| 80-89 | 8 | 15 | 0,75 |
| 90-99 | 5 | 20 | 1 |
[Ilustrasi gambar ogive dengan data contoh]
Mempelajari contoh soal histogram, poligon frekuensi, dan ogive bisa jadi menyenangkan, lho! Bayangkan, kamu bisa mengolah data tentang jumlah siswa di kelas, nilai ujian, atau bahkan jumlah penduduk di suatu daerah. Nah, untuk menguji pemahamanmu tentang pajak bumi dan bangunan (PBB), kamu bisa coba kerjakan contoh soal PBB dan jawabannya yang tersedia di internet.
Setelah itu, kamu bisa kembali fokus pada contoh soal histogram, poligon frekuensi, dan ogive untuk mengasah kemampuanmu dalam visualisasi data!
Gambar di atas menunjukkan grafik ogive yang dibuat berdasarkan data contoh. Titik-titik pada grafik tersebut adalah titik tengah kelas interval di sumbu x dan frekuensi kumulatif di sumbu y. Titik-titik tersebut kemudian dihubungkan dengan garis lurus. Garis yang dihasilkan adalah ogive.
Kelebihan dan Kekurangan Histogram, Poligon Frekuensi, dan Ogive: Contoh Soal Histogram Poligon Frekuensi Dan Ogive
Setelah mempelajari cara membuat histogram, poligon frekuensi, dan ogive, penting untuk memahami kelebihan dan kekurangan masing-masing diagram. Pemahaman ini membantu kita memilih diagram yang paling tepat untuk menampilkan data dan mengkomunikasikan informasi secara efektif.
Kelebihan dan Kekurangan Histogram
Histogram merupakan diagram yang menampilkan distribusi frekuensi data dengan menggunakan batang-batang yang saling berdekatan. Berikut kelebihan dan kekurangan histogram:
- Kelebihan:
- Menampilkan distribusi data dengan jelas, memudahkan identifikasi pola dan tren.
- Mudah dibuat dan dipahami, cocok untuk visualisasi data yang kompleks.
- Memungkinkan perbandingan data antar kelompok atau periode.
- Kekurangan:
- Tidak menunjukkan nilai data individual, hanya menampilkan frekuensi data dalam setiap kelas.
- Rentan terhadap perubahan ukuran kelas, yang dapat memengaruhi bentuk histogram.
- Tidak cocok untuk data yang memiliki banyak kelas atau data yang sangat terdistribusi.
Kelebihan dan Kekurangan Poligon Frekuensi
Poligon frekuensi adalah diagram yang menampilkan distribusi frekuensi data dengan menggunakan garis yang menghubungkan titik-titik tengah setiap kelas. Berikut kelebihan dan kekurangan poligon frekuensi:
- Kelebihan:
- Menampilkan distribusi data dengan jelas dan mudah dipahami.
- Memungkinkan perbandingan data antar kelompok atau periode.
- Memperlihatkan tren data dengan lebih jelas dibandingkan histogram.
- Kekurangan:
- Tidak menunjukkan nilai data individual, hanya menampilkan frekuensi data dalam setiap kelas.
- Rentan terhadap perubahan ukuran kelas, yang dapat memengaruhi bentuk poligon frekuensi.
- Tidak cocok untuk data yang memiliki banyak kelas atau data yang sangat terdistribusi.
Kelebihan dan Kekurangan Ogive
Ogive adalah diagram yang menampilkan frekuensi kumulatif data. Berikut kelebihan dan kekurangan ogive:
- Kelebihan:
- Menampilkan frekuensi kumulatif data, sehingga memudahkan untuk melihat berapa banyak data yang berada di bawah atau di atas nilai tertentu.
- Memungkinkan untuk menentukan persentil, kuartil, dan median data.
- Memperlihatkan distribusi data secara keseluruhan, termasuk konsentrasi data di bagian tertentu.
- Kekurangan:
- Tidak menunjukkan nilai data individual, hanya menampilkan frekuensi kumulatif data.
- Sulit untuk membandingkan data antar kelompok atau periode.
- Tidak cocok untuk menampilkan data yang memiliki banyak kelas atau data yang sangat terdistribusi.
Tabel Perbandingan Kelebihan dan Kekurangan
| Diagram | Kelebihan | Kekurangan |
|---|---|---|
| Histogram |
|
|
| Poligon Frekuensi |
|
|
| Ogive |
|
|
Kapan Penggunaan Setiap Diagram Paling Efektif?
Pilihan diagram yang tepat tergantung pada jenis data yang ingin ditampilkan dan tujuan analisis. Berikut beberapa contoh kapan penggunaan setiap diagram paling efektif:
- Histogram: Digunakan untuk menampilkan distribusi data numerik, seperti tinggi badan siswa, nilai ujian, atau jumlah kendaraan yang melintas di jalan raya.
- Poligon Frekuensi: Digunakan untuk menampilkan tren data, seperti pertumbuhan penjualan, perubahan suhu, atau jumlah pasien yang dirawat di rumah sakit.
- Ogive: Digunakan untuk menampilkan frekuensi kumulatif data, seperti jumlah penduduk yang berusia di bawah 18 tahun, atau jumlah karyawan yang memiliki gaji di atas rata-rata.
Penutupan Akhir
Dengan memahami konsep histogram, poligon frekuensi, dan ogive, kita dapat menyajikan data dengan cara yang lebih informatif dan mudah dipahami. Ketiga diagram ini tidak hanya membantu dalam visualisasi data, tetapi juga dalam analisis dan pengambilan keputusan yang lebih efektif. Jadi, jangan ragu untuk menggunakan diagram-diagram ini dalam berbagai bidang kehidupan untuk mendapatkan pemahaman yang lebih mendalam tentang data!