Contoh soal hots matematika – Bosan dengan soal matematika yang itu-itu saja? Ingin menguji kemampuan berpikirmu lebih dalam? Yuk, kita bahas contoh soal HOTS (Higher Order Thinking Skills) dalam matematika! Soal-soal ini dirancang untuk melatih kemampuan berpikir tingkat tinggi, seperti menganalisis, mengevaluasi, dan menciptakan solusi baru. Tak hanya mengasah otak, soal HOTS juga membantu memahami konsep matematika secara lebih mendalam dan mengembangkan kemampuan memecahkan masalah dalam kehidupan sehari-hari.
Soal HOTS dalam matematika hadir dalam berbagai kategori, mulai dari soal yang menuntut kemampuan menganalisis data hingga soal yang menantangmu untuk merumuskan strategi penyelesaian yang kreatif. Siap-siap diuji kemampuan berpikir kritis dan logikamu!
Kategori Soal HOTS Matematika
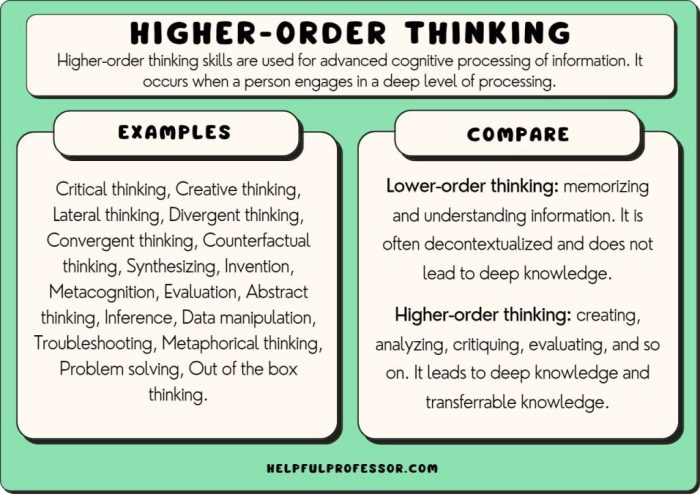
Soal HOTS (Higher Order Thinking Skills) dalam matematika dirancang untuk menguji kemampuan berpikir tingkat tinggi siswa. Kemampuan berpikir tingkat tinggi ini mencakup kemampuan menganalisis, mengevaluasi, dan menciptakan solusi baru berdasarkan pemahaman konsep yang sudah dimiliki.
Soal HOTS matematika dibagi menjadi beberapa kategori berdasarkan tingkatan kognitif yang diujikan. Berikut adalah penjelasan mengenai kategori soal HOTS matematika:
Analisis
Kategori soal analisis dalam matematika mengharuskan siswa untuk menguraikan informasi yang diberikan dan mengidentifikasi hubungan antar komponennya. Soal-soal analisis menuntut siswa untuk memahami struktur dan pola dalam suatu masalah, kemudian mengidentifikasi hubungan antar variabel atau konsep.
- Menentukan faktor-faktor yang mempengaruhi hasil suatu perhitungan.
- Mengidentifikasi pola atau tren dalam suatu data.
- Membedah langkah-langkah dalam suatu penyelesaian masalah.
Contoh Soal:
“Sebuah toko menjual dua jenis produk, A dan B. Produk A dijual dengan harga Rp10.000 per unit, sedangkan produk B dijual dengan harga Rp15.000 per unit. Jika dalam satu hari toko tersebut menjual 50 unit produk A dan 30 unit produk B, analisislah faktor-faktor yang mempengaruhi total pendapatan toko tersebut.”
Evaluasi
Kategori soal evaluasi dalam matematika menuntut siswa untuk menilai informasi yang diberikan dan membuat keputusan berdasarkan kriteria tertentu. Soal-soal evaluasi mendorong siswa untuk membandingkan, menilai, dan memberikan justifikasi atas pilihan yang mereka buat.
- Menilai kebenaran suatu pernyataan matematika.
- Membandingkan dua metode penyelesaian masalah dan menentukan metode yang lebih efektif.
- Menilai keefektifan suatu strategi dalam menyelesaikan masalah.
Contoh Soal:
“Dua siswa, A dan B, menyelesaikan soal persamaan linear dengan metode yang berbeda. Siswa A menggunakan metode eliminasi, sedangkan siswa B menggunakan metode substitusi. Evaluasilah kedua metode tersebut dan tentukan metode mana yang lebih efektif dalam menyelesaikan soal tersebut.”
Kreativitas
Kategori soal kreativitas dalam matematika mendorong siswa untuk menghasilkan solusi baru atau ide orisinal berdasarkan pemahaman konsep yang sudah dimiliki. Soal-soal kreativitas menuntut siswa untuk berpikir out of the box dan mengembangkan solusi yang inovatif.
- Merancang model matematika untuk suatu fenomena nyata.
- Menemukan solusi alternatif untuk suatu masalah matematika.
- Mengembangkan strategi baru untuk menyelesaikan masalah matematika.
Contoh Soal:
“Sebuah taman berbentuk persegi panjang dengan panjang 10 meter dan lebar 5 meter. Rancanglah model matematika untuk menghitung luas taman tersebut jika panjang dan lebarnya diubah.”
Penerapan
Kategori soal penerapan dalam matematika menuntut siswa untuk menggunakan pengetahuan matematika yang sudah dimiliki untuk menyelesaikan masalah dunia nyata. Soal-soal penerapan mengharuskan siswa untuk mengidentifikasi konsep matematika yang relevan dengan situasi nyata dan menerapkannya untuk menemukan solusi.
- Menggunakan konsep matematika untuk menyelesaikan masalah keuangan.
- Menerapkan prinsip-prinsip geometri dalam arsitektur.
- Menggunakan konsep statistik untuk menganalisis data penelitian.
Contoh Soal:
“Sebuah perusahaan ingin membangun sebuah gedung baru. Mereka ingin menghitung biaya pembangunan gedung tersebut. Gunakan konsep matematika untuk membantu perusahaan tersebut menghitung biaya pembangunan gedung tersebut.”
Pemecahan Masalah
Kategori soal pemecahan masalah dalam matematika mendorong siswa untuk menggunakan pengetahuan dan keterampilan matematika untuk menyelesaikan masalah kompleks. Soal-soal pemecahan masalah mengharuskan siswa untuk menganalisis masalah, merumuskan strategi, dan mengevaluasi solusi yang ditemukan.
- Menyelesaikan masalah matematika yang melibatkan beberapa konsep.
- Menggunakan strategi pemecahan masalah untuk menyelesaikan masalah matematika yang kompleks.
- Mengevaluasi solusi yang ditemukan dan menentukan apakah solusi tersebut tepat.
Contoh Soal:
“Sebuah toko ingin menentukan harga jual produk baru. Mereka ingin memastikan bahwa harga jual tersebut kompetitif dan menguntungkan. Gunakan strategi pemecahan masalah untuk membantu toko tersebut menentukan harga jual produk baru tersebut.”
Tabel Kategori Soal HOTS Matematika
| Kategori | Deskripsi | Contoh Soal |
|---|---|---|
| Analisis | Menguraikan informasi dan mengidentifikasi hubungan antar komponen. | “Sebuah toko menjual dua jenis produk, A dan B. Produk A dijual dengan harga Rp10.000 per unit, sedangkan produk B dijual dengan harga Rp15.000 per unit. Jika dalam satu hari toko tersebut menjual 50 unit produk A dan 30 unit produk B, analisislah faktor-faktor yang mempengaruhi total pendapatan toko tersebut.” |
| Evaluasi | Menilai informasi dan membuat keputusan berdasarkan kriteria tertentu. | “Dua siswa, A dan B, menyelesaikan soal persamaan linear dengan metode yang berbeda. Siswa A menggunakan metode eliminasi, sedangkan siswa B menggunakan metode substitusi. Evaluasilah kedua metode tersebut dan tentukan metode mana yang lebih efektif dalam menyelesaikan soal tersebut.” |
| Kreativitas | Menghasilkan solusi baru atau ide orisinal. | “Sebuah taman berbentuk persegi panjang dengan panjang 10 meter dan lebar 5 meter. Rancanglah model matematika untuk menghitung luas taman tersebut jika panjang dan lebarnya diubah.” |
| Penerapan | Menggunakan pengetahuan matematika untuk menyelesaikan masalah dunia nyata. | “Sebuah perusahaan ingin membangun sebuah gedung baru. Mereka ingin menghitung biaya pembangunan gedung tersebut. Gunakan konsep matematika untuk membantu perusahaan tersebut menghitung biaya pembangunan gedung tersebut.” |
| Pemecahan Masalah | Menggunakan pengetahuan dan keterampilan matematika untuk menyelesaikan masalah kompleks. | “Sebuah toko ingin menentukan harga jual produk baru. Mereka ingin memastikan bahwa harga jual tersebut kompetitif dan menguntungkan. Gunakan strategi pemecahan masalah untuk membantu toko tersebut menentukan harga jual produk baru tersebut.” |
Contoh Soal HOTS Matematika Berdasarkan Materi
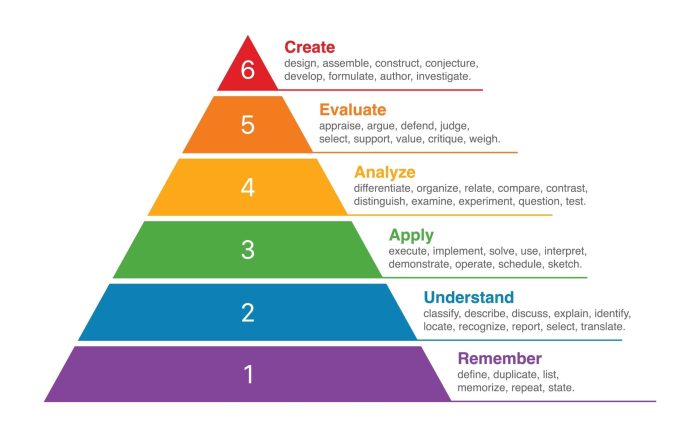
Soal HOTS (Higher Order Thinking Skills) merupakan jenis soal yang menuntut kemampuan berpikir tingkat tinggi. Soal HOTS dirancang untuk menguji kemampuan siswa dalam menganalisis, mengevaluasi, dan menciptakan solusi berdasarkan pemahaman konsep yang mendalam. Dalam artikel ini, kita akan menjelajahi contoh soal HOTS untuk beberapa materi matematika, yaitu aljabar, geometri, dan kalkulus. Kita akan menguraikan langkah-langkah penyelesaian dan penjelasan yang rinci untuk membantu Anda memahami bagaimana soal-soal ini dirancang dan bagaimana cara menyelesaikannya.
Aljabar
Soal HOTS aljabar biasanya menuntut siswa untuk memanipulasi persamaan, menyelesaikan sistem persamaan, atau menerapkan konsep aljabar dalam situasi yang lebih kompleks.
-
Contoh soal:
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Biaya produksi produk A adalah Rp 10.000 per unit, sedangkan biaya produksi produk B adalah Rp 15.000 per unit. Perusahaan memiliki anggaran Rp 1.000.000 untuk produksi. Jika perusahaan ingin memproduksi sebanyak mungkin unit, berapa banyak unit produk A dan B yang harus diproduksi?
Langkah penyelesaian:
-
Misalkan x adalah jumlah unit produk A dan y adalah jumlah unit produk B.
-
Buatlah persamaan berdasarkan informasi yang diberikan:
10.000x + 15.000y = 1.000.000
-
Selesaikan persamaan tersebut untuk mencari nilai x dan y. Anda dapat menggunakan metode substitusi atau eliminasi.
-
Pastikan solusi yang Anda dapatkan masuk akal dalam konteks soal. Jumlah unit produk A dan B haruslah bilangan bulat positif.
Penjelasan:
Soal ini menuntut siswa untuk merumuskan persamaan berdasarkan informasi yang diberikan dan menyelesaikannya untuk menemukan solusi optimal. Ini melibatkan pemahaman konsep aljabar, termasuk persamaan linear, dan kemampuan untuk menerapkannya dalam situasi dunia nyata.
-
Geometri
Soal HOTS geometri biasanya melibatkan pengaplikasian rumus dan teorema geometri dalam situasi yang tidak biasa atau menuntut pemahaman yang mendalam tentang konsep-konsep geometri.
-
Contoh soal:
Sebuah segitiga ABC memiliki sisi AB = 10 cm, BC = 8 cm, dan AC = 6 cm. Titik D terletak pada sisi BC sehingga AD adalah garis bagi sudut BAC. Tentukan panjang BD.
Langkah penyelesaian:
-
Gambarlah segitiga ABC dan titik D pada sisi BC.
-
Terapkan teorema garis bagi sudut:
BD/DC = AB/AC
-
Substitusikan nilai yang diketahui:
BD/(8-BD) = 10/6
-
Selesaikan persamaan tersebut untuk mencari nilai BD.
Penjelasan:
Soal ini menuntut siswa untuk menerapkan teorema garis bagi sudut dalam situasi yang lebih kompleks. Ini membutuhkan pemahaman yang mendalam tentang konsep geometri, termasuk teorema dan rumus yang terkait.
-
Kalkulus, Contoh soal hots matematika
Soal HOTS kalkulus biasanya melibatkan aplikasi konsep turunan, integral, dan limit dalam situasi yang lebih kompleks atau menuntut pemahaman yang lebih dalam tentang konsep-konsep kalkulus.
-
Contoh soal:
Sebuah benda bergerak dengan kecepatan v(t) = t^2 – 4t + 3 meter per detik. Tentukan jarak total yang ditempuh benda dalam interval waktu 0 ≤ t ≤ 4 detik.
Langkah penyelesaian:
-
Tentukan fungsi jarak s(t) dengan mengintegralkan fungsi kecepatan v(t):
s(t) = ∫(t^2 – 4t + 3) dt = (1/3)t^3 – 2t^2 + 3t + C
-
Tentukan konstanta integrasi C dengan menggunakan informasi awal. Misalkan s(0) = 0, maka C = 0.
-
Hitung jarak total yang ditempuh dalam interval 0 ≤ t ≤ 4 detik:
s(4) – s(0) = [(1/3)(4)^3 – 2(4)^2 + 3(4)] – 0 = 16/3 meter
Penjelasan:
Soal ini menuntut siswa untuk memahami hubungan antara kecepatan, jarak, dan turunan. Ini melibatkan pemahaman konsep integral dan kemampuan untuk menerapkannya dalam situasi yang lebih kompleks.
-
Contoh Soal HOTS yang Melibatkan Penggabungan Beberapa Konsep
Soal HOTS yang melibatkan penggabungan beberapa konsep dapat lebih menantang, namun juga lebih menarik karena menuntut siswa untuk berpikir kritis dan kreatif dalam mengaplikasikan pengetahuan mereka.
-
Contoh soal:
Sebuah perusahaan ingin membangun sebuah gudang berbentuk persegi panjang dengan luas 1000 meter persegi. Sisi gudang dibatasi oleh pagar dengan biaya Rp 100.000 per meter. Tentukan dimensi gudang yang menghasilkan biaya pagar minimum.
Langkah penyelesaian:
-
Misalkan panjang gudang adalah x meter dan lebar gudang adalah y meter.
-
Buatlah persamaan berdasarkan informasi yang diberikan:
xy = 1000 (luas gudang)
P = 2x + 2y (keliling gudang)
-
Tentukan fungsi biaya C(x) sebagai fungsi dari panjang x:
C(x) = 100.000(2x + 2y) = 200.000x + 200.000y
-
Substitusikan y = 1000/x ke dalam fungsi C(x):
C(x) = 200.000x + 200.000(1000/x)
-
Tentukan turunan pertama dari fungsi C(x) dan cari titik kritis:
C'(x) = 200.000 – 200.000(1000/x^2) = 0
-
Selesaikan persamaan tersebut untuk mencari nilai x. Kemudian, cari nilai y dengan menggunakan persamaan xy = 1000.
-
Tentukan dimensi gudang yang menghasilkan biaya pagar minimum.
Penjelasan:
Soal ini menggabungkan konsep aljabar (persamaan linear), geometri (luas dan keliling persegi panjang), dan kalkulus (turunan). Siswa perlu memahami konsep-konsep ini dan menerapkannya secara terintegrasi untuk menyelesaikan soal ini. Ini menunjukkan bahwa kemampuan berpikir tingkat tinggi tidak hanya melibatkan pemahaman konsep yang mendalam, tetapi juga kemampuan untuk menggabungkan dan menerapkan berbagai konsep dalam situasi yang kompleks.
-
Tips Menyusun Soal HOTS Matematika
Soal HOTS (Higher Order Thinking Skills) dalam matematika dirancang untuk menguji kemampuan berpikir tingkat tinggi siswa, seperti analisis, evaluasi, dan pemecahan masalah. Menyusun soal HOTS yang efektif dan menantang membutuhkan pemahaman yang mendalam tentang konsep matematika dan kemampuan untuk merancang pertanyaan yang mendorong siswa untuk berpikir kritis dan kreatif.
Tips Menyusun Soal HOTS Matematika
Berikut adalah beberapa tips dalam menyusun soal HOTS matematika yang efektif dan menantang:
- Fokus pada Konsep dan Prinsip: Soal HOTS matematika harus berfokus pada pemahaman konsep dan prinsip matematika, bukan hanya pada prosedur atau algoritma. Misalnya, alih-alih meminta siswa untuk menyelesaikan persamaan linear, mintalah mereka untuk menjelaskan hubungan antara persamaan linear dan grafiknya.
- Gunakan Konteks Sehari-hari: Soal HOTS matematika yang menarik dan relevan dengan kehidupan sehari-hari dapat memotivasi siswa untuk berpikir lebih dalam. Misalnya, Anda dapat meminta siswa untuk menghitung biaya bahan bangunan untuk membangun rumah atau menghitung jumlah bahan bakar yang dibutuhkan untuk perjalanan tertentu.
- Berikan Soal Terbuka: Soal HOTS matematika tidak selalu memiliki satu jawaban yang benar. Soal terbuka memungkinkan siswa untuk berpikir kreatif dan memberikan jawaban yang beragam, menunjukkan pemahaman mereka yang lebih dalam tentang konsep matematika.
- Dorong Analisis dan Interpretasi: Soal HOTS matematika harus mendorong siswa untuk menganalisis informasi, menginterpretasikan data, dan menarik kesimpulan. Misalnya, Anda dapat meminta siswa untuk menganalisis data tentang pertumbuhan penduduk dan memprediksi pertumbuhan di masa depan.
- Gunakan Strategi Berbeda: Soal HOTS matematika dapat disusun menggunakan berbagai strategi, seperti kasus studi, simulasi, atau permainan. Strategi ini dapat membuat pembelajaran lebih interaktif dan menarik bagi siswa.
Contoh Soal HOTS Matematika
Berikut adalah beberapa contoh soal HOTS matematika yang menguji kemampuan berpikir kritis dan kreatif:
- Contoh Soal 1:
Sebuah toko menjual dua jenis kue, kue A dan kue B. Kue A dijual dengan harga Rp 10.000 per potong dan kue B dijual dengan harga Rp 15.000 per potong. Seorang pembeli membeli 5 potong kue A dan 3 potong kue B. Berapa total uang yang harus dibayar pembeli? - Contoh Soal 2:
Sebuah taman berbentuk persegi panjang dengan panjang 10 meter dan lebar 5 meter. Di tengah taman terdapat kolam berbentuk lingkaran dengan diameter 3 meter. Hitunglah luas taman yang tidak termasuk kolam. - Contoh Soal 3:
Sebuah mobil melaju dengan kecepatan 60 km/jam. Berapa lama waktu yang dibutuhkan mobil untuk menempuh jarak 180 km?
Cara Membuat Soal HOTS Matematika yang Menarik dan Relevan
Untuk membuat soal HOTS matematika yang menarik dan relevan dengan kehidupan sehari-hari, Anda dapat mengikuti langkah-langkah berikut:
- Identifikasi Konsep Matematika yang Ingin Diuji: Tentukan konsep matematika yang ingin diuji melalui soal HOTS. Misalnya, jika Anda ingin menguji pemahaman siswa tentang persamaan linear, Anda dapat membuat soal yang berkaitan dengan situasi sehari-hari yang melibatkan persamaan linear.
- Cari Konteks yang Relevan: Cari konteks yang relevan dengan kehidupan sehari-hari yang dapat digunakan untuk menyusun soal. Misalnya, Anda dapat menggunakan konteks tentang keuangan, kesehatan, atau lingkungan.
- Buat Soal yang Menarik dan Menggugah Rasa Ingin Tahu: Soal HOTS matematika harus menarik dan menggugah rasa ingin tahu siswa. Anda dapat menggunakan gambar, video, atau cerita untuk membuat soal lebih menarik.
- Berikan Soal yang Menantang: Soal HOTS matematika harus menantang siswa untuk berpikir kritis dan kreatif. Anda dapat memberikan soal yang membutuhkan analisis, interpretasi, dan evaluasi.
- Sediakan Petunjuk yang Jelas: Berikan petunjuk yang jelas tentang apa yang diharapkan dari siswa dalam menyelesaikan soal. Anda dapat menggunakan kata kunci seperti “jelaskan”, “analisis”, atau “evaluasi”.
Pentingnya Soal HOTS dalam Pembelajaran Matematika
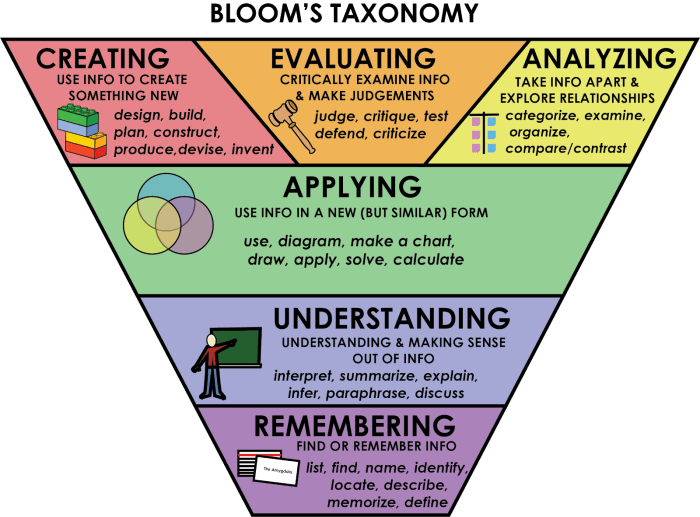
Dalam dunia pendidikan yang terus berkembang, penting untuk memastikan bahwa siswa tidak hanya menguasai konsep matematika dasar, tetapi juga mampu berpikir kritis, memecahkan masalah, dan menerapkan pengetahuan mereka dalam konteks yang berbeda. Soal HOTS (Higher Order Thinking Skills) memainkan peran penting dalam mencapai tujuan pembelajaran ini.
Manfaat Penggunaan Soal HOTS dalam Pembelajaran Matematika
Penggunaan soal HOTS dalam pembelajaran matematika memiliki banyak manfaat, baik untuk siswa maupun guru. Berikut beberapa di antaranya:
- Meningkatkan Kemampuan Berpikir Kritis: Soal HOTS mendorong siswa untuk menganalisis informasi, mengevaluasi argumen, dan membentuk kesimpulan berdasarkan pemahaman mereka. Hal ini membantu mereka mengembangkan kemampuan berpikir kritis yang penting dalam berbagai aspek kehidupan.
- Memperkuat Pemahaman Konsep: Soal HOTS menuntut siswa untuk menghubungkan konsep matematika dengan situasi nyata dan memecahkan masalah kompleks. Proses ini membantu mereka memahami konsep matematika dengan lebih mendalam dan tidak hanya menghafal rumus.
- Meningkatkan Kemampuan Pemecahan Masalah: Soal HOTS dirancang untuk melatih siswa dalam memecahkan masalah yang tidak memiliki solusi langsung. Mereka harus berpikir kreatif, menemukan strategi baru, dan menerapkan pengetahuan mereka secara fleksibel.
- Mengembangkan Kemampuan Komunikasi Matematika: Soal HOTS seringkali mengharuskan siswa untuk menjelaskan proses berpikir mereka, menjustifikasi jawaban mereka, dan berkomunikasi ide-ide matematika dengan jelas dan terstruktur.
- Meningkatkan Motivasi dan Minat Belajar: Soal HOTS yang menantang dan menarik dapat memotivasi siswa untuk belajar lebih dalam dan mengembangkan rasa ingin tahu mereka terhadap matematika.
Cara Soal HOTS Meningkatkan Kemampuan Berpikir Siswa
Soal HOTS dirancang untuk merangsang kemampuan berpikir tingkat tinggi pada siswa, yang meliputi:
- Analisis: Soal HOTS mendorong siswa untuk memecah masalah menjadi bagian-bagian yang lebih kecil, mengidentifikasi pola, dan menemukan hubungan antar komponen.
- Sintesis: Soal HOTS menuntut siswa untuk menggabungkan informasi yang berbeda, menciptakan ide-ide baru, dan mengembangkan solusi inovatif.
- Evaluasi: Soal HOTS mendorong siswa untuk menilai informasi, menilai argumen, dan membuat keputusan berdasarkan kriteria yang jelas.
- Kreativitas: Soal HOTS mendorong siswa untuk berpikir di luar kotak, menemukan solusi yang tidak konvensional, dan mengeksplorasi kemungkinan yang berbeda.
Strategi Pembelajaran yang Mengintegrasikan Soal HOTS
Untuk mencapai tujuan pembelajaran yang efektif dengan mengintegrasikan soal HOTS, berikut beberapa strategi yang dapat diterapkan:
- Mulailah dengan Soal HOTS Sederhana: Awali dengan soal HOTS yang relatif sederhana dan secara bertahap tingkatkan tingkat kesulitannya seiring dengan kemampuan siswa.
- Berikan Waktu Cukup: Soal HOTS membutuhkan waktu untuk dipecahkan. Berikan waktu yang cukup bagi siswa untuk berpikir, menganalisis, dan menyelesaikan masalah.
- Dorong Diskusi dan Kolaborasi: Dorong siswa untuk berdiskusi dan berkolaborasi dalam memecahkan soal HOTS. Hal ini dapat membantu mereka mendapatkan perspektif yang berbeda dan mengembangkan strategi bersama.
- Gunakan Berbagai Jenis Soal HOTS: Gunakan berbagai jenis soal HOTS, seperti soal esai, soal terbuka, soal proyek, dan soal simulasi, untuk merangsang berbagai kemampuan berpikir.
- Berikan Umpan Balik yang Konstruktif: Berikan umpan balik yang konstruktif kepada siswa setelah mereka menyelesaikan soal HOTS. Jelaskan proses berpikir yang benar dan bantu mereka memahami kesalahan mereka.
- Integrasikan Soal HOTS dengan Materi Pelajaran: Jangan hanya menggunakan soal HOTS sebagai latihan terpisah. Integrasikan soal HOTS dengan materi pelajaran untuk membantu siswa memahami konsep dan menerapkannya dalam konteks yang berbeda.
Penutupan: Contoh Soal Hots Matematika
Melalui contoh soal HOTS matematika, kita diajak untuk berpikir lebih kritis, kreatif, dan inovatif. Tak hanya untuk meraih nilai bagus, soal HOTS juga membantu kita dalam menghadapi tantangan di dunia nyata. Jadi, jangan takut untuk menghadapi soal-soal yang menantang. Dengan latihan dan semangat belajar, kita dapat menguasai kemampuan berpikir tingkat tinggi dan meraih hasil yang maksimal dalam pembelajaran matematika.





