Contoh Soal Irisan Kerucut Hiperbola dan Pembahasannya: Kuasai Konsep dan Selesaikan Soal dengan Mudah

Pernahkah kamu mendengar tentang irisan kerucut hiperbola? Bentuknya yang unik dan rumit mungkin membuatmu penasaran. Hiperbola merupakan salah satu dari empat jenis irisan kerucut, selain parabola, elips, dan lingkaran. Bentuknya seperti dua lengkungan terbuka yang saling berhadapan dan memiliki titik fokus yang berbeda. Dalam artikel ini, kita akan membahas tentang contoh soal irisan kerucut hiperbola dan pembahasannya, sehingga kamu dapat memahami konsepnya dengan lebih mudah.

Hiperbola memiliki persamaan umum yang unik dan rumit, namun jangan khawatir! Dengan mempelajari elemen-elemennya seperti pusat, sumbu simetri, fokus, dan asimtot, kamu dapat menentukan persamaan hiperbola dari informasi yang diberikan. Selain itu, kamu juga akan belajar cara menyelesaikan berbagai jenis soal irisan kerucut hiperbola, mulai dari menentukan persamaan hingga menggambar grafiknya. Artikel ini akan memberikan contoh soal dan pembahasan yang lengkap, sehingga kamu dapat mempraktikkan dan mengasah kemampuanmu dalam menyelesaikan soal irisan kerucut hiperbola.

Pengertian Irisan Kerucut Hiperbola

Irisan kerucut hiperbola merupakan salah satu bentuk kurva yang dihasilkan dari irisan antara kerucut dengan bidang yang memotong kedua sisi kerucut. Bentuk hiperbola memiliki dua cabang simetris yang terbuka ke arah yang berlawanan.

Ilustrasi Bentuk Hiperbola

Bayangkan sebuah kerucut terpotong oleh bidang yang miring. Bidang ini memotong kedua sisi kerucut dan membentuk dua kurva terbuka yang saling berhadapan. Kurva ini disebut hiperbola. Ilustrasi sederhana ini menunjukkan bagaimana hiperbola terbentuk sebagai irisan kerucut.

Persamaan Umum Hiperbola dan Elemen-Elemennya

Persamaan umum hiperbola dapat dinyatakan dalam berbagai bentuk, tergantung pada orientasi sumbu simetrinya. Berikut ini adalah persamaan umum hiperbola dan elemen-elemennya:

• Persamaan Umum Hiperbola:
  • Bentuk standar hiperbola dengan sumbu simetri horizontal:
    
    

    (x – h)² / a² – (y – k)² / b² = 1

  • Bentuk standar hiperbola dengan sumbu simetri vertikal:
    
    

    (y – k)² / a² – (x – h)² / b² = 1

• Elemen-elemen Hiperbola:
  • Pusat (h, k): Titik tengah antara kedua fokus dan titik potong kedua sumbu simetri.
  • Sumbu Simetri: Garis yang membagi hiperbola menjadi dua bagian yang simetris.
  • Fokus (F1, F2): Dua titik tetap yang menentukan hiperbola. Jarak antara setiap titik pada hiperbola dengan kedua fokus adalah konstan.
  • Sumbu Transversal (2a): Jarak antara kedua titik potong hiperbola dengan sumbu simetri.
  • Sumbu Konjugasi (2b): Jarak antara kedua titik potong hiperbola dengan sumbu tegak lurus terhadap sumbu simetri.
  • Asymptote: Dua garis lurus yang didekati hiperbola ketika x atau y mendekati tak terhingga.

Cara Menentukan Persamaan Hiperbola

Hiperbola adalah kurva yang dibentuk oleh semua titik yang selisih jaraknya ke dua titik tetap (disebut fokus) adalah konstan. Persamaan hiperbola dapat ditentukan dengan beberapa cara, tergantung pada informasi yang diberikan.

Langkah-Langkah Menentukan Persamaan Hiperbola

Untuk menentukan persamaan hiperbola, kita perlu mengetahui beberapa informasi penting, seperti:

• Pusat hiperbola (h, k)
• Fokus hiperbola (h ± c, k) atau (h, k ± c)
• Sumbu simetri hiperbola (horizontal atau vertikal)
• Nilai a dan b, di mana a adalah jarak dari pusat ke titik potong hiperbola dengan sumbu simetri dan b adalah jarak dari pusat ke titik potong hiperbola dengan garis tegak lurus terhadap sumbu simetri yang melalui pusat.

Setelah kita mengetahui informasi tersebut, kita dapat menentukan persamaan hiperbola dengan mengikuti langkah-langkah berikut:

1. Tentukan bentuk umum persamaan hiperbola berdasarkan orientasi sumbu simetrinya.
   • Jika sumbu simetrinya horizontal, persamaannya adalah
     

     (x – h)²/a² – (y – k)²/b² = 1

   • Jika sumbu simetrinya vertikal, persamaannya adalah
     

     (y – k)²/a² – (x – h)²/b² = 1

2. Gunakan informasi tentang pusat hiperbola (h, k) untuk mengganti nilai h dan k dalam persamaan umum.
3. Gunakan informasi tentang fokus hiperbola untuk menentukan nilai c. Ingat bahwa c² = a² + b².
4. Gunakan informasi tentang sumbu simetri dan nilai a untuk menentukan nilai b.
5. Substitusikan nilai a, b, h, dan k ke dalam persamaan umum hiperbola yang telah ditentukan pada langkah pertama.

Contoh Soal dan Pembahasan

Misalkan kita ingin menentukan persamaan hiperbola dengan pusat di titik (2, 1), fokus di titik (2, 5), dan sumbu simetri vertikal.

Berikut langkah-langkah untuk menentukan persamaan hiperbola:

1. Karena sumbu simetrinya vertikal, persamaan umum hiperbola adalah
   

   (y – k)²/a² – (x – h)²/b² = 1

2. Pusat hiperbola adalah (2, 1), sehingga h = 2 dan k = 1. Persamaan hiperbola menjadi:
   

   (y – 1)²/a² – (x – 2)²/b² = 1

3. Fokus hiperbola adalah (2, 5), sehingga c = 5 – 1 = 4.
4. Kita tahu bahwa c² = a² + b². Dari informasi yang diberikan, kita hanya mengetahui nilai c, sehingga kita perlu mencari nilai a terlebih dahulu.
   
   Untuk mencari nilai a, kita dapat menggunakan informasi bahwa sumbu simetrinya vertikal. Ini berarti bahwa titik potong hiperbola dengan sumbu simetri berada pada titik (2, 1 + a) dan (2, 1 – a).
   
   Jarak dari pusat hiperbola ke titik potong hiperbola dengan sumbu simetri adalah a, sehingga a = 4.
   
   Sekarang kita dapat mencari nilai b dengan menggunakan persamaan c² = a² + b². Substitusikan nilai c dan a yang sudah kita ketahui:
   

   4² = 4² + b²

   Maka b² = 0, sehingga b = 0.

5. Substitusikan nilai a, b, h, dan k ke dalam persamaan umum hiperbola:
   

   (y – 1)²/4² – (x – 2)²/0² = 1

   Karena b = 0, persamaan hiperbola menjadi:

   (y – 1)²/16 = 1

Jadi, persamaan hiperbola dengan pusat di titik (2, 1), fokus di titik (2, 5), dan sumbu simetri vertikal adalah (y – 1)²/16 = 1.

Persamaan Umum Hiperbola dan Contohnya

Sumbu Simetri	Persamaan Umum	Contoh
Horizontal	(x – h)²/a² – (y – k)²/b² = 1	(x – 2)²/9 – (y + 1)²/4 = 1
Vertikal	(y – k)²/a² – (x – h)²/b² = 1	(y – 3)²/16 – (x + 1)²/9 = 1

Jenis-Jenis Soal Irisan Kerucut Hiperbola

Hiperbola merupakan salah satu jenis irisan kerucut yang memiliki bentuk unik dan menarik. Soal-soal tentang hiperbola umumnya menguji pemahaman kita tentang persamaan hiperbola, sifat-sifatnya, dan penerapannya dalam berbagai bidang. Dalam pembahasan ini, kita akan menjelajahi berbagai jenis soal hiperbola yang sering muncul dan bagaimana cara mengatasinya.

Menentukan Persamaan Hiperbola

Jenis soal ini menuntut kita untuk menentukan persamaan hiperbola berdasarkan informasi yang diberikan. Informasi tersebut bisa berupa titik fokus, titik puncak, atau panjang sumbu transversa.

• Contoh soal: Tentukan persamaan hiperbola dengan titik fokus (5, 0) dan (-5, 0) serta titik puncak (4, 0) dan (-4, 0).
• Cara menentukan persamaan hiperbola:
  1. Tentukan posisi hiperbola: Karena titik fokus berada pada sumbu x dan titik puncak juga berada pada sumbu x, maka hiperbola berorientasi horizontal.
  2. Tentukan nilai a dan c: Dari titik puncak, kita dapatkan a = 4. Dari titik fokus, kita dapatkan c = 5.
  3. Hitung nilai b: Gunakan rumus b² = c² – a². Dalam kasus ini, b² = 25 – 16 = 9, sehingga b = 3.
  4. Tentukan persamaan hiperbola: Karena hiperbola berorientasi horizontal, persamaannya adalah (x²/a²) – (y²/b²) = 1. Substitusikan nilai a dan b, sehingga persamaan hiperbolanya adalah (x²/16) – (y²/9) = 1.

Menentukan Sifat-Sifat Hiperbola, Contoh soal irisan kerucut hiperbola dan pembahasannya

Jenis soal ini meminta kita untuk menentukan sifat-sifat hiperbola seperti titik fokus, titik puncak, asimtot, dan panjang sumbu transversa dan sumbu konjugasi.

• Contoh soal: Tentukan titik fokus, titik puncak, asimtot, dan panjang sumbu transversa dan sumbu konjugasi dari hiperbola dengan persamaan (x²/9) – (y²/16) = 1.
• Cara menentukan sifat-sifat hiperbola:
  1. Tentukan posisi hiperbola: Karena x² memiliki koefisien positif, hiperbola berorientasi horizontal.
  2. Tentukan nilai a dan b: Dari persamaan, kita dapatkan a = 3 dan b = 4.
  3. Hitung nilai c: Gunakan rumus c² = a² + b². Dalam kasus ini, c² = 9 + 16 = 25, sehingga c = 5.
  4. Tentukan titik fokus: Titik fokus terletak pada sumbu x dan berjarak c dari pusat hiperbola. Jadi, titik fokusnya adalah (5, 0) dan (-5, 0).
  5. Tentukan titik puncak: Titik puncak terletak pada sumbu x dan berjarak a dari pusat hiperbola. Jadi, titik puncaknya adalah (3, 0) dan (-3, 0).
  6. Tentukan persamaan asimtot: Persamaan asimtot hiperbola horizontal adalah y = ±(b/a)x. Jadi, persamaan asimtotnya adalah y = ±(4/3)x.
  7. Tentukan panjang sumbu transversa: Panjang sumbu transversa adalah 2a, sehingga panjangnya adalah 6.
  8. Tentukan panjang sumbu konjugasi: Panjang sumbu konjugasi adalah 2b, sehingga panjangnya adalah 8.

Menentukan Jenis Hiperbola

Soal jenis ini meminta kita untuk menentukan apakah hiperbola berorientasi horizontal atau vertikal berdasarkan persamaannya.

• Contoh soal: Tentukan jenis hiperbola dengan persamaan (y²/25) – (x²/16) = 1.
• Cara menentukan jenis hiperbola:
  1. Perhatikan koefisien x² dan y²: Dalam persamaan ini, koefisien y² positif dan koefisien x² negatif.
  2. Tentukan jenis hiperbola: Jika koefisien y² positif, maka hiperbola berorientasi vertikal. Jika koefisien x² positif, maka hiperbola berorientasi horizontal.

Menyelesaikan Soal Irisan Kerucut Hiperbola

Hiperbola merupakan salah satu jenis irisan kerucut yang memiliki bentuk seperti dua kurva yang terbuka dan simetris. Untuk menyelesaikan soal irisan kerucut hiperbola, diperlukan pemahaman yang kuat tentang sifat-sifat dan persamaan hiperbola.

Langkah-Langkah Umum Menyelesaikan Soal Irisan Kerucut Hiperbola

Berikut adalah langkah-langkah umum yang dapat digunakan untuk menyelesaikan soal irisan kerucut hiperbola:

1. Menganalisis Soal dan Menentukan Jenis Hiperbola: Langkah pertama adalah memahami soal dan menentukan jenis hiperbola yang terlibat. Apakah hiperbola tersebut horizontal atau vertikal? Apakah titik pusatnya di (0,0) atau di titik lain? Informasi ini dapat diperoleh dari persamaan hiperbola atau dari informasi yang diberikan dalam soal.
2. Menentukan Titik Pusat dan As-As Hiperbola: Setelah menentukan jenis hiperbola, langkah selanjutnya adalah menentukan titik pusat dan as-as hiperbola. Titik pusat merupakan titik tengah dari segmen garis yang menghubungkan kedua fokus hiperbola. As-as hiperbola merupakan garis lurus yang melalui titik pusat dan sejajar dengan sumbu simetri hiperbola.
3. Menentukan Nilai a, b, dan c: Nilai a, b, dan c merupakan nilai-nilai penting yang digunakan dalam persamaan hiperbola. Nilai a adalah jarak dari titik pusat ke titik puncak, nilai b adalah jarak dari titik pusat ke titik fokus, dan nilai c adalah jarak dari titik pusat ke titik fokus.
4. Menentukan Persamaan Hiperbola: Setelah menentukan nilai a, b, dan c, kita dapat menentukan persamaan hiperbola. Persamaan hiperbola dapat ditulis dalam bentuk standar, yaitu:

   Untuk hiperbola horizontal: (x-h)^2/a^2 – (y-k)^2/b^2 = 1

   Untuk hiperbola vertikal: (y-k)^2/a^2 – (x-h)^2/b^2 = 1

   Dimana (h,k) adalah titik pusat hiperbola.

5. Menentukan Elemen-Elemen Lain dari Hiperbola: Setelah menentukan persamaan hiperbola, kita dapat menentukan elemen-elemen lain dari hiperbola, seperti titik fokus, titik puncak, asimtot, dan eksentrisitas.

Contoh Soal dan Pembahasan

Berikut adalah contoh soal dan pembahasan untuk menyelesaikan soal irisan kerucut hiperbola:

Soal:

Tentukan persamaan hiperbola dengan titik pusat (2,1), titik fokus (5,1), dan titik puncak (3,1).

Pembahasan:

Contoh soal irisan kerucut hiperbola dan pembahasannya bisa membantu kamu memahami konsep dasar dan cara menyelesaikan soal-soal yang berkaitan dengan hiperbola. Misalnya, soal yang meminta kamu menentukan persamaan hiperbola dari titik fokus dan sumbu simetris. Soal seperti ini akan melatih kemampuanmu dalam mengaplikasikan rumus dan konsep hiperbola.

Selain contoh soal irisan kerucut hiperbola, kamu juga bisa menemukan contoh soal rekonsiliasi fiskal dan jawabannya di sini. Rekonsiliasi fiskal sendiri merupakan proses penting dalam memahami selisih antara penghasilan bruto dan penghasilan kena pajak, dan soal-soal yang terkait dengannya dapat membantu kamu memperdalam pemahaman mengenai aspek pajak dan akuntansi.

Dengan mempelajari berbagai contoh soal, kamu akan semakin siap menghadapi berbagai tantangan dan soal-soal yang mungkin muncul di ujian atau dalam pekerjaanmu kelak.

1. Menganalisis Soal dan Menentukan Jenis Hiperbola: Dari soal diketahui bahwa titik pusat hiperbola berada di (2,1) dan titik fokus berada di (5,1). Karena titik fokus dan titik pusat memiliki ordinat yang sama, maka hiperbola tersebut adalah hiperbola horizontal.
2. Menentukan Titik Pusat dan As-As Hiperbola: Titik pusat hiperbola sudah diketahui, yaitu (2,1). As-as hiperbola adalah garis lurus yang melalui titik pusat dan sejajar dengan sumbu simetri hiperbola. Karena hiperbola horizontal, maka as-as hiperbola sejajar dengan sumbu x.
3. Menentukan Nilai a, b, dan c: Nilai a adalah jarak dari titik pusat ke titik puncak, yaitu a = 3 – 2 = 1. Nilai c adalah jarak dari titik pusat ke titik fokus, yaitu c = 5 – 2 = 3. Nilai b dapat dihitung dengan menggunakan rumus b^2 = c^2 – a^2, sehingga b^2 = 3^2 – 1^2 = 8. Jadi, b = √8 = 2√2.
4. Menentukan Persamaan Hiperbola: Persamaan hiperbola horizontal adalah (x-h)^2/a^2 – (y-k)^2/b^2 = 1. Dengan mensubstitusikan nilai h = 2, k = 1, a = 1, dan b = 2√2, maka persamaan hiperbola tersebut adalah:

   (x-2)^2/1^2 – (y-1)^2/(2√2)^2 = 1

   Atau

   (x-2)^2 – (y-1)^2/8 = 1

Tips dan Trik Menyelesaikan Soal Irisan Kerucut Hiperbola

Berikut adalah beberapa tips dan trik untuk menyelesaikan soal irisan kerucut hiperbola dengan mudah:

• Pahami sifat-sifat dan persamaan hiperbola dengan baik.
• Gunakan diagram untuk memvisualisasikan soal dan membantu menentukan elemen-elemen hiperbola.
• Latih soal-soal yang berbeda untuk meningkatkan pemahaman dan kemampuan menyelesaikan soal.

Aplikasi Irisan Kerucut Hiperbola

Hiperbola, salah satu jenis irisan kerucut, memiliki aplikasi yang menarik dalam berbagai bidang. Bentuknya yang khas, dengan dua cabang yang terbuka ke arah tak terhingga, memungkinkan hiperbola untuk memainkan peran penting dalam teknologi dan ilmu pengetahuan.

Antena Parabola

Salah satu contoh aplikasi hiperbola yang paling umum adalah dalam antena parabola. Antena parabola menggunakan reflektor berbentuk parabola untuk memfokuskan gelombang elektromagnetik, seperti gelombang radio atau gelombang cahaya. Prinsip kerja antena parabola didasarkan pada sifat refleksi hiperbola, di mana setiap sinar yang datang dari sumber di salah satu fokus hiperbola akan dipantulkan menuju fokus lainnya.

Antena parabola memiliki dua fokus, yaitu fokus utama dan fokus sekunder. Sinyal yang diterima oleh antena parabola dari sumber jauh akan dipantulkan oleh reflektor parabola menuju fokus utama. Di fokus utama, sinyal tersebut akan dikumpulkan oleh sebuah penerima, yang kemudian mengolah sinyal tersebut. Dengan cara ini, antena parabola mampu menangkap dan memfokuskan sinyal yang lemah dari sumber yang jauh, seperti satelit komunikasi atau stasiun radio.

Teleskop Reflekt

Teleskop reflektor, seperti Teleskop Hubble, menggunakan cermin berbentuk parabola untuk mengumpulkan dan memfokuskan cahaya dari objek langit. Cermin parabola pada teleskop reflektor memiliki dua fokus, yaitu fokus utama dan fokus sekunder. Cahaya dari objek langit akan dipantulkan oleh cermin parabola menuju fokus utama. Di fokus utama, cahaya tersebut akan dikumpulkan oleh sebuah lensa atau cermin sekunder, yang kemudian memantulkan cahaya tersebut menuju fokus sekunder. Di fokus sekunder, cahaya tersebut akan ditangkap oleh detektor, seperti kamera atau sensor cahaya, untuk menghasilkan gambar objek langit.

Lensa Hiperbolik

Lensa hiperbolik adalah lensa yang memiliki permukaan berbentuk hiperbola. Lensa hiperbolik digunakan dalam berbagai aplikasi optik, seperti mikroskop, teleskop, dan sistem pencitraan. Lensa hiperbolik memiliki sifat unik yang memungkinkan mereka untuk memfokuskan cahaya dari berbagai sudut, menghasilkan gambar yang tajam dan berkualitas tinggi.

Prinsip kerja lensa hiperbolik didasarkan pada sifat refraksi hiperbola. Cahaya yang melewati lensa hiperbolik akan dibiaskan (dibelokkan) oleh permukaan hiperbola, sehingga cahaya tersebut akan difokuskan pada titik tertentu. Titik fokus ini dapat berada di depan atau di belakang lensa, tergantung pada bentuk dan orientasi lensa hiperbolik.

Gerak Planet

Dalam astronomi, orbit planet-planet di sekitar matahari dapat dimodelkan dengan menggunakan hiperbola. Orbit planet-planet biasanya berbentuk elips, tetapi jika sebuah planet memiliki kecepatan yang cukup tinggi, orbitnya dapat menjadi hiperbola.

Gerak planet-planet dalam orbit hiperbola didasarkan pada hukum gravitasi Newton. Hukum gravitasi Newton menyatakan bahwa setiap benda di alam semesta menarik benda lainnya dengan gaya yang sebanding dengan massa kedua benda dan berbanding terbalik dengan kuadrat jarak antara keduanya.

Ketika sebuah planet bergerak dengan kecepatan tinggi, gaya gravitasi matahari tidak cukup kuat untuk menahan planet tersebut dalam orbit elips. Sebagai hasilnya, planet tersebut akan bergerak dalam orbit hiperbola, yang berarti bahwa planet tersebut akan melarikan diri dari sistem tata surya.

Soal Latihan Irisan Kerucut Hiperbola

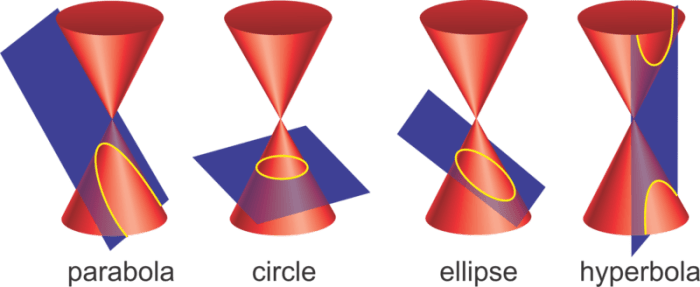
Hiperbola adalah salah satu jenis irisan kerucut yang memiliki bentuk lengkung terbuka. Dalam mempelajari hiperbola, penting untuk memahami sifat-sifatnya dan cara menentukan persamaannya. Berikut ini adalah contoh soal latihan irisan kerucut hiperbola dengan tingkat kesulitan yang bervariasi, beserta pembahasan lengkapnya.

Contoh Soal Latihan Irisan Kerucut Hiperbola

Untuk memahami lebih lanjut tentang irisan kerucut hiperbola, mari kita selesaikan beberapa contoh soal latihan berikut.

1. Tentukan persamaan hiperbola dengan pusat di titik (2, -1), sumbu transversal sepanjang 6, dan sumbu konjugat sepanjang 8.

2. Tentukan titik fokus dan persamaan asimtot hiperbola dengan persamaan
   $$ \frac(x – 1)^29 – \frac(y + 2)^216 = 1. $$

3. Tentukan persamaan hiperbola yang memiliki titik fokus di (5, 0) dan (-5, 0) dan melalui titik (4, 3).

4. Tentukan persamaan hiperbola yang memiliki sumbu transversal sepanjang 10, sumbu konjugat sepanjang 6, dan titik puncak di (3, 0) dan (-3, 0).

5. Tentukan persamaan hiperbola yang memiliki titik fokus di (0, 5) dan (0, -5) dan melalui titik (4, 3).

Pembahasan Soal Latihan Irisan Kerucut Hiperbola

Berikut adalah pembahasan lengkap untuk setiap soal latihan yang telah diberikan.

Soal 1

Diketahui pusat hiperbola di titik (2, -1), sumbu transversal sepanjang 6, dan sumbu konjugat sepanjang 8. Persamaan hiperbola dengan pusat di (h, k) adalah:

$$ \frac(x – h)^2a^2 – \frac(y – k)^2b^2 = 1. $$

Dengan demikian, persamaan hiperbola yang dicari adalah:

$$ \frac(x – 2)^23^2 – \frac(y + 1)^24^2 = 1. $$

Jadi, persamaan hiperbola yang dicari adalah

$$ \frac(x – 2)^29 – \frac(y + 1)^216 = 1. $$

Soal 2

Persamaan hiperbola yang diberikan adalah:

$$ \frac(x – 1)^29 – \frac(y + 2)^216 = 1. $$

Dari persamaan ini, kita dapat mengetahui bahwa:

• Pusat hiperbola di titik (1, -2).
• Sumbu transversal sepanjang 2a = 6, sehingga a = 3.
• Sumbu konjugat sepanjang 2b = 8, sehingga b = 4.

Titik fokus hiperbola terletak di titik (h ± c, k), di mana c adalah jarak dari pusat ke titik fokus. Nilai c dapat dihitung dengan menggunakan rumus:

$$ c^2 = a^2 + b^2. $$

Dengan demikian, c = 5. Titik fokus hiperbola adalah (1 ± 5, -2), yaitu (6, -2) dan (-4, -2). Persamaan asimtot hiperbola adalah:

$$ y – k = \pm \fracba (x – h). $$

Dengan demikian, persamaan asimtot hiperbola adalah:

$$ y + 2 = \pm \frac43 (x – 1). $$

Soal 3

Diketahui titik fokus hiperbola di (5, 0) dan (-5, 0). Hal ini menunjukkan bahwa hiperbola memiliki sumbu transversal horizontal. Pusat hiperbola terletak di tengah-tengah kedua titik fokus, yaitu di titik (0, 0). Jarak dari pusat ke titik fokus adalah c = 5.

Diketahui hiperbola melalui titik (4, 3). Jarak dari titik (4, 3) ke pusat hiperbola adalah 5. Dengan demikian, jarak dari titik (4, 3) ke titik fokus adalah:

$$ \sqrt4^2 + 3^2 = 5. $$

Hal ini menunjukkan bahwa titik (4, 3) terletak pada sumbu transversal hiperbola. Dengan demikian, a = 4.

Nilai b dapat dihitung dengan menggunakan rumus:

$$ c^2 = a^2 + b^2. $$

Dengan demikian, b = 3.

Persamaan hiperbola dengan pusat di (0, 0) dan sumbu transversal horizontal adalah:

$$ \fracx^2a^2 – \fracy^2b^2 = 1. $$

Dengan demikian, persamaan hiperbola yang dicari adalah:

$$ \fracx^216 – \fracy^29 = 1. $$

Soal 4

Diketahui sumbu transversal sepanjang 10, sumbu konjugat sepanjang 6, dan titik puncak di (3, 0) dan (-3, 0). Hal ini menunjukkan bahwa hiperbola memiliki sumbu transversal horizontal. Pusat hiperbola terletak di tengah-tengah kedua titik puncak, yaitu di titik (0, 0). Sumbu transversal sepanjang 2a = 10, sehingga a = 5. Sumbu konjugat sepanjang 2b = 6, sehingga b = 3.

Persamaan hiperbola dengan pusat di (0, 0) dan sumbu transversal horizontal adalah:

$$ \fracx^2a^2 – \fracy^2b^2 = 1. $$

Dengan demikian, persamaan hiperbola yang dicari adalah:

$$ \fracx^225 – \fracy^29 = 1. $$

Soal 5

Diketahui titik fokus hiperbola di (0, 5) dan (0, -5). Hal ini menunjukkan bahwa hiperbola memiliki sumbu transversal vertikal. Pusat hiperbola terletak di tengah-tengah kedua titik fokus, yaitu di titik (0, 0). Jarak dari pusat ke titik fokus adalah c = 5.

Diketahui hiperbola melalui titik (4, 3). Jarak dari titik (4, 3) ke pusat hiperbola adalah 5. Dengan demikian, jarak dari titik (4, 3) ke titik fokus adalah:

$$ \sqrt4^2 + 3^2 = 5. $$

Hal ini menunjukkan bahwa titik (4, 3) terletak pada sumbu transversal hiperbola. Dengan demikian, b = 3.

Nilai a dapat dihitung dengan menggunakan rumus:

$$ c^2 = a^2 + b^2. $$

Dengan demikian, a = 4.

Persamaan hiperbola dengan pusat di (0, 0) dan sumbu transversal vertikal adalah:

$$ \fracy^2b^2 – \fracx^2a^2 = 1. $$

Dengan demikian, persamaan hiperbola yang dicari adalah:

$$ \fracy^29 – \fracx^216 = 1. $$

Rumus dan Teorema Irisan Kerucut Hiperbola

Hiperbola merupakan salah satu jenis irisan kerucut yang memiliki bentuk lengkung terbuka. Untuk memahami hiperbola lebih dalam, kita perlu mempelajari rumus dan teorema penting yang berkaitan dengannya. Rumus dan teorema ini akan membantu kita untuk menentukan persamaan hiperbola, menentukan titik-titik penting seperti pusat, fokus, dan sumbu simetri, serta menghitung jarak antar titik-titik tersebut.

Persamaan Hiperbola

Persamaan hiperbola dapat dibagi menjadi dua bentuk, yaitu persamaan hiperbola horizontal dan persamaan hiperbola vertikal. Persamaan hiperbola horizontal memiliki sumbu simetri horizontal, sedangkan persamaan hiperbola vertikal memiliki sumbu simetri vertikal.

• Persamaan Hiperbola Horizontal:
  

  (x-h)²/a² – (y-k)²/b² = 1

• Persamaan Hiperbola Vertikal:
  

  (y-k)²/a² – (x-h)²/b² = 1

Dimana:

• (h,k) adalah titik pusat hiperbola
• a adalah jarak dari titik pusat ke titik puncak hiperbola
• b adalah jarak dari titik pusat ke titik ujung sumbu konjugasi

Titik Fokus dan Sumbu Simetri

Titik fokus hiperbola adalah titik-titik yang terletak pada sumbu simetri hiperbola dan memiliki jarak yang sama dari titik pusat hiperbola. Jarak ini disebut sebagai jarak fokus (c). Sumbu simetri hiperbola adalah garis yang membagi hiperbola menjadi dua bagian yang sama.

• Jarak Fokus (c):
  

  c² = a² + b²

• Titik Fokus Hiperbola Horizontal:
  

  (h ± c, k)

• Titik Fokus Hiperbola Vertikal:
  

  (h, k ± c)

• Sumbu Simetri Hiperbola Horizontal:
  

  y = k

• Sumbu Simetri Hiperbola Vertikal:
  

  x = h

Asimtot Hiperbola

Asimtot hiperbola adalah garis lurus yang mendekati hiperbola saat x atau y mendekati tak terhingga. Asimtot hiperbola membantu kita untuk menentukan bentuk hiperbola secara keseluruhan.

• Persamaan Asimtot Hiperbola Horizontal:
  

  y – k = ± (b/a)(x – h)

• Persamaan Asimtot Hiperbola Vertikal:
  

  x – h = ± (a/b)(y – k)

Contoh Soal dan Pembahasan

Diketahui persamaan hiperbola (x-2)²/9 – (y+1)²/16 = 1. Tentukan titik pusat, titik fokus, sumbu simetri, dan persamaan asimtot hiperbola tersebut.

Pembahasan:

• Titik Pusat: (h,k) = (2,-1)
• Jarak Fokus (c): c² = a² + b² = 9 + 16 = 25, maka c = 5
• Titik Fokus: (h ± c, k) = (2 ± 5, -1) = (7, -1) dan (-3, -1)
• Sumbu Simetri: y = k = -1
• Persamaan Asimtot: y – k = ± (b/a)(x – h) = ± (4/3)(x – 2)

Aspek Geometri Irisan Kerucut Hiperbola

Hiperbola, sebagai salah satu irisan kerucut, memiliki karakteristik geometri unik yang membedakannya dari parabola dan elips. Aspek geometri ini berperan penting dalam memahami bentuk, posisi, dan sifat-sifat hiperbola.

Fokus dan Sumbu Simetri

Hiperbola memiliki dua titik fokus (F1 dan F2) yang terletak pada sumbu simetrinya. Sumbu simetri merupakan garis lurus yang membagi hiperbola menjadi dua bagian yang identik. Jarak antara kedua fokus ini disebut jarak fokus (2c). Titik tengah antara kedua fokus merupakan titik pusat hiperbola (O).

• Jarak antara titik sembarang pada hiperbola (P) dengan salah satu fokus (F1) dikurangi jarak titik tersebut dengan fokus lainnya (F2) selalu konstan dan sama dengan jarak fokus (2c).
• Persamaan hiperbola yang berpusat di (0, 0) dengan sumbu simetri horizontal adalah:
  

  x²/a² – y²/b² = 1

• Persamaan hiperbola yang berpusat di (0, 0) dengan sumbu simetri vertikal adalah:
  

  y²/a² – x²/b² = 1

Asimtot

Asimtot merupakan garis lurus yang didekati oleh hiperbola saat titik-titik pada hiperbola semakin menjauh dari titik pusat. Hiperbola memiliki dua asimtot yang saling tegak lurus dan berpotongan di titik pusat hiperbola.

• Persamaan asimtot hiperbola yang berpusat di (0, 0) dengan sumbu simetri horizontal adalah:
  

  y = ±(b/a)x

• Persamaan asimtot hiperbola yang berpusat di (0, 0) dengan sumbu simetri vertikal adalah:
  

  x = ±(a/b)y

Contoh Soal dan Pembahasan

Misalnya, sebuah hiperbola memiliki fokus di (5, 0) dan (-5, 0), serta titik puncak di (3, 0) dan (-3, 0). Tentukan persamaan hiperbola dan persamaan asimtotnya.

• Dari informasi yang diberikan, diketahui jarak fokus (2c) = 10 dan panjang sumbu transversal (2a) = 6. Sehingga, nilai c = 5 dan a = 3.
• Untuk mencari nilai b, kita gunakan rumus: c² = a² + b².
  

  b² = c² – a² = 5² – 3² = 16

  Maka, b = 4.

• Karena fokus terletak pada sumbu x, maka persamaan hiperbola adalah:
  

  x²/a² – y²/b² = 1

  Substitusikan nilai a dan b:

  x²/3² – y²/4² = 1

  Sehingga, persamaan hiperbola adalah:

  x²/9 – y²/16 = 1

• Persamaan asimtot hiperbola adalah:
  

  y = ±(b/a)x

  Substitusikan nilai a dan b:

  y = ±(4/3)x

Contoh Soal Ujian Irisan Kerucut Hiperbola: Contoh Soal Irisan Kerucut Hiperbola Dan Pembahasannya

Hiperbola merupakan salah satu jenis irisan kerucut yang memiliki bentuk lengkung simetris dengan dua titik fokus. Dalam mempelajari hiperbola, kita akan menemukan berbagai konsep penting seperti persamaan, fokus, sumbu simetri, dan asimtot. Untuk menguji pemahaman tentang materi ini, berikut adalah beberapa contoh soal ujian irisan kerucut hiperbola dengan tingkat kesulitan yang berbeda.

Soal 1: Menentukan Persamaan Hiperbola

Soal ini dirancang untuk menguji kemampuan Anda dalam menentukan persamaan hiperbola berdasarkan informasi yang diberikan.

1. Tentukan persamaan hiperbola yang memiliki titik fokus di (5,0) dan (-5,0) dan sumbu transversa sepanjang 8.

Soal 2: Menentukan Elemen Hiperbola

Soal ini dirancang untuk menguji kemampuan Anda dalam menentukan elemen-elemen penting dari hiperbola berdasarkan persamaannya.

1. Tentukan titik fokus, sumbu transversa, sumbu konjugata, dan asimtot dari hiperbola dengan persamaan (x^2/16) – (y^2/9) = 1.

Soal 3: Menentukan Persamaan Hiperbola dari Grafik

Soal ini dirancang untuk menguji kemampuan Anda dalam menentukan persamaan hiperbola berdasarkan grafiknya.

1. Tentukan persamaan hiperbola yang memiliki grafik seperti gambar di bawah ini.
   [Gambar Hiperbola]

Poin-Poin Penting yang Harus Diperhatikan dalam Menjawab Soal Ujian

Berikut adalah beberapa poin penting yang harus diperhatikan dalam menjawab soal ujian irisan kerucut hiperbola:

• Pahami konsep dasar hiperbola, seperti definisi, persamaan, dan elemen-elemen pentingnya.
• Mampu menentukan persamaan hiperbola dari informasi yang diberikan, seperti titik fokus, sumbu transversa, dan sumbu konjugata.
• Mampu menentukan elemen-elemen penting dari hiperbola berdasarkan persamaannya, seperti titik fokus, sumbu transversa, sumbu konjugata, dan asimtot.
• Mampu menggambar grafik hiperbola berdasarkan persamaannya.
• Latih soal-soal latihan yang sejenis untuk meningkatkan pemahaman dan kemampuan dalam menyelesaikan soal ujian.

Kunci Jawaban dan Pembahasan

Soal 1:

Diketahui titik fokus di (5,0) dan (-5,0), sehingga jarak antara kedua titik fokus adalah 10. Karena sumbu transversa sepanjang 8, maka jarak antara kedua titik ujung sumbu transversa adalah 8. Dengan demikian, jarak antara titik fokus dan titik ujung sumbu transversa adalah 10/2 = 5.

Berdasarkan rumus jarak antara titik fokus dan titik ujung sumbu transversa, yaitu c = √(a^2 + b^2), kita dapat menentukan nilai b:

5 = √(4^2 + b^2)

25 = 16 + b^2

b^2 = 9

b = 3

Karena titik fokus berada pada sumbu x, maka persamaan hiperbola adalah:

(x^2/a^2) – (y^2/b^2) = 1

(x^2/16) – (y^2/9) = 1

Jadi, persamaan hiperbola yang memiliki titik fokus di (5,0) dan (-5,0) dan sumbu transversa sepanjang 8 adalah (x^2/16) – (y^2/9) = 1.

Soal 2:

Persamaan hiperbola adalah (x^2/16) – (y^2/9) = 1.

Dari persamaan tersebut, kita dapat menentukan:

a^2 = 16, sehingga a = 4

b^2 = 9, sehingga b = 3

c^2 = a^2 + b^2 = 16 + 9 = 25, sehingga c = 5

Titik fokus: (c, 0) dan (-c, 0) = (5, 0) dan (-5, 0)

Sumbu transversa: 2a = 8

Sumbu konjugata: 2b = 6

Asimtot: y = ±(b/a)x = ±(3/4)x

Soal 3:

Dari gambar hiperbola, kita dapat menentukan bahwa titik fokus berada pada sumbu x, sehingga persamaan hiperbola adalah (x^2/a^2) – (y^2/b^2) = 1.

Titik ujung sumbu transversa berada pada (4, 0) dan (-4, 0), sehingga a = 4.

Titik ujung sumbu konjugata berada pada (0, 3) dan (0, -3), sehingga b = 3.

Dengan demikian, persamaan hiperbola adalah (x^2/16) – (y^2/9) = 1.

Kesulitan dalam Memahami Irisan Kerucut Hiperbola

Hiperbola, salah satu jenis irisan kerucut, seringkali menjadi momok bagi siswa dalam mempelajari matematika. Konsepnya yang abstrak dan rumit, serta penerapannya dalam kehidupan sehari-hari yang mungkin tidak langsung terlihat, menjadi tantangan tersendiri. Memahami hiperbola dengan baik membutuhkan pemahaman yang kuat tentang konsep dasar geometri, aljabar, dan kemampuan untuk menghubungkan teori dengan aplikasi praktisnya.

Identifikasi Kesulitan Umum

Beberapa kesulitan umum yang dihadapi siswa dalam memahami hiperbola adalah:

• Kesulitan dalam memahami definisi hiperbola. Definisi hiperbola sebagai himpunan titik-titik yang selisih jaraknya ke dua titik tetap (fokus) adalah konstan, seringkali sulit dipahami secara intuitif.
• Kesulitan dalam memahami persamaan hiperbola. Persamaan hiperbola, baik dalam bentuk standar maupun umum, mengandung banyak variabel dan konstanta yang saling berkaitan, sehingga siswa seringkali kesulitan dalam mengidentifikasi dan menginterpretasikan makna masing-masing variabel.
• Kesulitan dalam memvisualisasikan hiperbola. Hiperbola memiliki bentuk yang unik, dengan dua cabang yang terentang tak hingga. Kesulitan dalam memvisualisasikan bentuk ini dapat menghambat pemahaman tentang sifat-sifat hiperbola.
• Kesulitan dalam mengaplikasikan konsep hiperbola dalam masalah nyata. Siswa seringkali kesulitan dalam menghubungkan konsep hiperbola dengan aplikasi praktisnya, seperti dalam bidang astronomi, fisika, atau teknik.

Solusi dan Strategi untuk Mengatasi Kesulitan

Untuk mengatasi kesulitan tersebut, beberapa solusi dan strategi dapat diterapkan:

• Mulailah dengan memahami definisi hiperbola secara intuitif. Gunakan ilustrasi dan contoh sederhana untuk memperkenalkan definisi hiperbola. Misalnya, gunakan contoh dua titik fokus dan sebuah titik yang bergerak sehingga selisih jaraknya ke kedua titik fokus selalu sama.
• Fokus pada pemahaman persamaan hiperbola. Mulailah dengan mempelajari bentuk standar persamaan hiperbola dan kemudian beralih ke bentuk umum. Gunakan contoh dan latihan untuk membantu siswa dalam memahami makna masing-masing variabel dan konstanta.
• Gunakan visualisasi untuk membantu pemahaman. Gunakan software geometri atau gambar-gambar untuk membantu siswa memvisualisasikan bentuk hiperbola dan sifat-sifatnya. Visualisasi dapat membantu siswa dalam memahami konsep abstrak dengan lebih mudah.
• Hubungkan konsep hiperbola dengan aplikasi praktis. Berikan contoh aplikasi hiperbola dalam bidang astronomi, fisika, atau teknik. Contoh-contoh ini dapat membantu siswa dalam memahami relevansi konsep hiperbola dalam kehidupan nyata.
• Gunakan pendekatan bertahap. Hindari mengajarkan semua konsep hiperbola sekaligus. Mulailah dengan konsep dasar dan kemudian secara bertahap perkenalkan konsep yang lebih kompleks.

Pendekatan yang Lebih Mudah Dipahami

Salah satu pendekatan yang lebih mudah dipahami adalah dengan menggunakan analogi dan perbandingan. Misalnya, dapat dijelaskan bahwa hiperbola merupakan bentuk lengkung yang mirip dengan parabola, namun memiliki dua cabang yang terentang tak hingga. Selain itu, dapat dijelaskan bahwa hiperbola memiliki beberapa sifat yang mirip dengan elips, seperti memiliki dua fokus dan eksentrisitas.

Penting untuk diingat bahwa memahami hiperbola membutuhkan waktu dan latihan. Siswa harus diberikan kesempatan untuk berlatih menyelesaikan masalah dan mengaplikasikan konsep hiperbola dalam berbagai konteks. Dengan pendekatan yang tepat dan latihan yang cukup, siswa dapat mengatasi kesulitan dalam memahami hiperbola dan menguasai konsep ini dengan baik.

Pemungkas

Setelah mempelajari contoh soal irisan kerucut hiperbola dan pembahasannya, kamu diharapkan dapat memahami konsep hiperbola dengan lebih baik. Dengan menguasai rumus, teorema, dan langkah-langkah dalam menyelesaikan soal, kamu dapat menghadapi berbagai jenis soal irisan kerucut hiperbola dengan percaya diri. Ingat, kunci utama dalam mempelajari matematika adalah latihan! Semakin banyak soal yang kamu kerjakan, semakin mahir kamu dalam menyelesaikannya. Selamat belajar!