Contoh Soal dan Jawaban Trigonometri: Kuasai Konsep dan Aplikasi Trigonometri

Contoh soal jawaban trigonometri – Trigonometri, cabang matematika yang mempelajari hubungan antara sudut dan sisi dalam segitiga, merupakan topik yang menarik dan memiliki aplikasi luas dalam berbagai bidang, seperti navigasi, astronomi, dan arsitektur. Mempelajari trigonometri tidak hanya tentang menghafal rumus, tetapi juga memahami konsep dan penerapannya dalam memecahkan masalah nyata.

Untuk membantu Anda memahami konsep dan aplikasi trigonometri, artikel ini akan membahas contoh soal dan jawaban trigonometri yang mencakup berbagai jenis soal, mulai dari soal dasar hingga soal yang menantang kemampuan berpikir tingkat tinggi (HOTS). Dengan mempelajari contoh-contoh ini, Anda akan mendapatkan pemahaman yang lebih baik tentang bagaimana trigonometri digunakan dalam berbagai situasi.

Pengertian Trigonometri: Contoh Soal Jawaban Trigonometri

Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut dalam segitiga. Trigonometri berasal dari kata Yunani “trigonon” yang berarti “tiga sudut” dan “metron” yang berarti “mengukur”. Dalam trigonometri, kita menggunakan fungsi trigonometri seperti sinus (sin), cosinus (cos), dan tangen (tan) untuk menghitung panjang sisi, besar sudut, dan berbagai besaran lainnya dalam segitiga.

Penerapan Trigonometri dalam Kehidupan Sehari-hari

Trigonometri memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti:

• Navigasi: Trigonometri digunakan dalam sistem GPS untuk menentukan lokasi dan arah.
• Arsitektur: Trigonometri digunakan untuk menghitung sudut dan panjang sisi dalam desain bangunan.
• Teknik Sipil: Trigonometri digunakan untuk menghitung kekuatan dan stabilitas struktur, seperti jembatan dan gedung.
• Astronomi: Trigonometri digunakan untuk menghitung jarak dan ukuran bintang dan planet.
• Fisika: Trigonometri digunakan untuk menganalisis gerakan benda dan gelombang.

Rumus-Rumus Dasar Trigonometri

Berikut adalah beberapa rumus dasar trigonometri yang sering digunakan:

Rumus	Keterangan
sin θ = sisi depan / sisi miring	Sinus sudut θ adalah perbandingan antara panjang sisi depan dan sisi miring dalam segitiga siku-siku.
cos θ = sisi samping / sisi miring	Cosinus sudut θ adalah perbandingan antara panjang sisi samping dan sisi miring dalam segitiga siku-siku.
tan θ = sisi depan / sisi samping	Tangen sudut θ adalah perbandingan antara panjang sisi depan dan sisi samping dalam segitiga siku-siku.
cot θ = sisi samping / sisi depan	Cotangen sudut θ adalah kebalikan dari tangen, yaitu perbandingan antara panjang sisi samping dan sisi depan dalam segitiga siku-siku.
sec θ = sisi miring / sisi samping	Sekan sudut θ adalah kebalikan dari cosinus, yaitu perbandingan antara panjang sisi miring dan sisi samping dalam segitiga siku-siku.
csc θ = sisi miring / sisi depan	Kosekan sudut θ adalah kebalikan dari sinus, yaitu perbandingan antara panjang sisi miring dan sisi depan dalam segitiga siku-siku.

Jenis-jenis Soal Trigonometri

Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi-sisi segitiga. Dalam trigonometri, terdapat berbagai macam jenis soal yang dapat dijumpai, mulai dari soal dasar hingga soal yang lebih kompleks. Memahami jenis-jenis soal trigonometri akan membantu kita dalam menyelesaikan masalah trigonometri dengan lebih mudah dan efektif.

Soal Identitas Trigonometri, Contoh soal jawaban trigonometri

Soal identitas trigonometri merupakan soal yang mengharuskan kita untuk membuktikan persamaan trigonometri yang diberikan. Persamaan ini biasanya melibatkan fungsi-fungsi trigonometri seperti sinus, cosinus, tangen, cotangen, secan, dan cosecan. Untuk menyelesaikan soal identitas trigonometri, kita dapat menggunakan berbagai macam strategi, seperti:

• Mengubah semua fungsi trigonometri ke dalam bentuk sinus dan cosinus.
• Menggunakan rumus-rumus trigonometri yang sudah diketahui.
• Mengalikan kedua ruas persamaan dengan faktor yang sama.
• Membagi kedua ruas persamaan dengan faktor yang sama.
• Menyederhanakan persamaan dengan menggunakan sifat-sifat trigonometri.

Contoh soal identitas trigonometri:

Buktikan bahwa:

sin²x + cos²x = 1

Penyelesaian:

1. Rumus identitas trigonometri yang digunakan: sin²x + cos²x = 1
2. Oleh karena rumus yang digunakan adalah rumus identitas trigonometri, maka persamaan tersebut sudah terpenuhi.
3. Jadi, sin²x + cos²x = 1 terbukti.

Soal Mencari Nilai Sudut

Soal mencari nilai sudut merupakan soal yang mengharuskan kita untuk menentukan nilai sudut dari suatu fungsi trigonometri. Untuk menyelesaikan soal ini, kita dapat menggunakan berbagai macam cara, seperti:

• Menggunakan tabel trigonometri.
• Menggunakan kalkulator trigonometri.
• Menggunakan rumus-rumus trigonometri yang sudah diketahui.

Contoh soal mencari nilai sudut:

Tentukan nilai sudut x yang memenuhi persamaan:

sin x = 1/2

Penyelesaian:

1. Berdasarkan tabel trigonometri, nilai sin x = 1/2 didapatkan pada sudut x = 30 derajat.
2. Jadi, nilai sudut x yang memenuhi persamaan sin x = 1/2 adalah 30 derajat.

Soal Mencari Nilai Sisi

Soal mencari nilai sisi merupakan soal yang mengharuskan kita untuk menentukan panjang sisi dari suatu segitiga. Untuk menyelesaikan soal ini, kita dapat menggunakan berbagai macam cara, seperti:

• Menggunakan rumus-rumus trigonometri yang sudah diketahui.
• Menggunakan teorema Pythagoras.
• Menggunakan aturan sinus dan aturan cosinus.

Contoh soal mencari nilai sisi:

Suatu segitiga siku-siku memiliki panjang sisi miring 10 cm dan sudut lancip 30 derajat. Tentukan panjang sisi alas segitiga tersebut.

Penyelesaian:

1. Rumus trigonometri yang digunakan: cos x = sisi alas/sisi miring.
2. Berdasarkan rumus, sisi alas = sisi miring * cos x.
3. Sisi alas = 10 cm * cos 30 derajat = 10 cm * (√3/2) = 5√3 cm.
4. Jadi, panjang sisi alas segitiga tersebut adalah 5√3 cm.

Soal Aplikasi Trigonometri

Soal aplikasi trigonometri merupakan soal yang menggunakan konsep trigonometri untuk menyelesaikan masalah dalam kehidupan nyata. Soal ini biasanya melibatkan berbagai macam bidang, seperti fisika, teknik, dan arsitektur. Untuk menyelesaikan soal aplikasi trigonometri, kita perlu memahami konsep trigonometri dan mampu menerapkannya dalam konteks yang diberikan.

Contoh soal aplikasi trigonometri:

Sebuah pohon memiliki tinggi 15 meter. Sebuah tangga bersandar pada pohon dengan sudut 60 derajat terhadap tanah. Tentukan panjang tangga tersebut.

Penyelesaian:

1. Rumus trigonometri yang digunakan: sin x = sisi depan/sisi miring.
2. Berdasarkan rumus, sisi miring = sisi depan/sin x.
3. Sisi miring = 15 meter/sin 60 derajat = 15 meter/(√3/2) = 10√3 meter.
4. Jadi, panjang tangga tersebut adalah 10√3 meter.

Rumus-rumus Trigonometri

Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga. Rumus-rumus trigonometri sangat penting dalam menyelesaikan berbagai masalah matematika dan fisika, terutama yang melibatkan sudut dan jarak.

Nggak cuma soal trigonometri yang bikin kepala pusing, soal fisika tentang energi dan usaha juga bisa jadi tantangan! Contoh soal jawaban trigonometri biasanya melibatkan rumus-rumus sudut dan sisi segitiga, sementara contoh soal fisika energi dan usaha lebih fokus ke konsep kerja, gaya, dan perpindahan.

Tapi, tenang, dengan latihan yang cukup, kamu bisa menaklukkan keduanya! Soal trigonometri pun bisa jadi lebih mudah dipecahkan setelah kamu menguasai konsep energi dan usaha. Jadi, semangat belajarnya!

Rumus-rumus trigonometri dapat dibagi menjadi beberapa kelompok, yaitu identitas trigonometri, rumus penjumlahan dan pengurangan sudut, rumus sudut ganda, dan rumus sudut setengah.

Identitas Trigonometri

Identitas trigonometri adalah persamaan yang berlaku untuk semua nilai sudut. Identitas trigonometri digunakan untuk menyederhanakan ekspresi trigonometri dan menyelesaikan persamaan trigonometri.

Identitas	Keterangan
sin2 θ + cos2 θ = 1	Identitas Pythagoras
tan θ = sin θ / cos θ	Definisi tangen
cot θ = cos θ / sin θ	Definisi kotangen
sec θ = 1 / cos θ	Definisi sekan
csc θ = 1 / sin θ	Definisi kosekan

Contoh Penggunaan Rumus Trigonometri

Berikut adalah contoh soal yang menggunakan rumus trigonometri:

Diketahui segitiga siku-siku ABC dengan sudut siku-siku di C. Jika panjang sisi AB = 10 cm dan sudut A = 30°, tentukan panjang sisi BC.

Untuk menyelesaikan soal ini, kita dapat menggunakan rumus sinus:

sin A = BC / AB

Dengan mensubstitusikan nilai yang diketahui, kita mendapatkan:

sin 30° = BC / 10 cm

Karena sin 30° = 1/2, maka:

1/2 = BC / 10 cm

Dengan mengalikan kedua ruas dengan 10 cm, kita mendapatkan:

BC = 5 cm

Jadi, panjang sisi BC adalah 5 cm.

Contoh Soal Trigonometri

Berikut adalah contoh soal trigonometri yang memerlukan penggunaan rumus-rumus trigonometri:

Diketahui sin θ = 3/5 dan cos θ < 0. Tentukan nilai tan θ.

Untuk menyelesaikan soal ini, kita dapat menggunakan rumus identitas trigonometri:

tan θ = sin θ / cos θ

Kita sudah mengetahui nilai sin θ, tetapi kita perlu mencari nilai cos θ. Karena cos θ < 0, maka θ berada di kuadran II atau kuadran III. Di kuadran II, cos θ bernilai negatif dan sin θ bernilai positif. Di kuadran III, cos θ dan sin θ bernilai negatif.

Karena sin θ = 3/5, maka kita dapat menggunakan identitas Pythagoras untuk mencari nilai cos θ:

cos² θ = 1 – sin² θ

Dengan mensubstitusikan nilai sin θ, kita mendapatkan:

cos² θ = 1 – (3/5)² = 16/25

Karena cos θ < 0, maka cos θ = -4/5. Dengan demikian, nilai tan θ adalah:

tan θ = sin θ / cos θ = (3/5) / (-4/5) = -3/4

Jadi, nilai tan θ adalah -3/4.

Hubungan Sudut dan Sisi

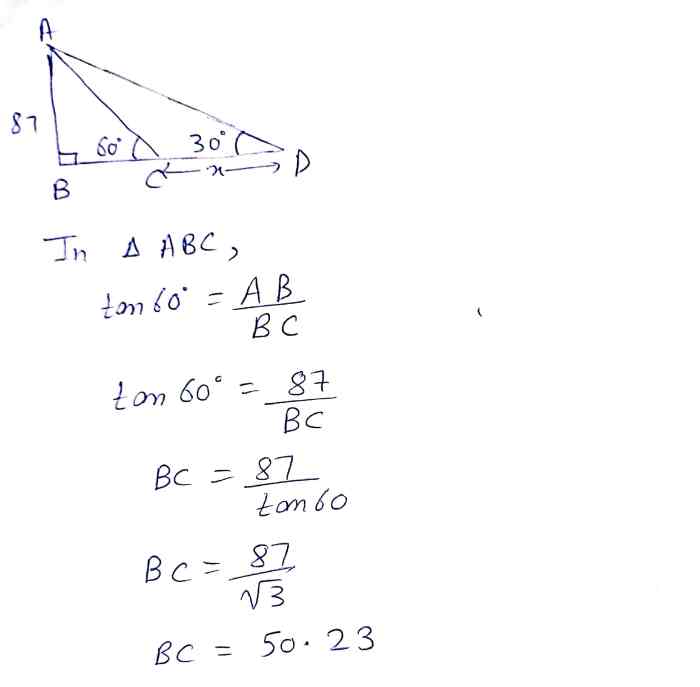
Dalam segitiga siku-siku, hubungan antara sudut dan sisi sangat penting dalam memahami konsep trigonometri. Hubungan ini didefinisikan melalui rasio sisi-sisi yang membentuk sudut-sudut tertentu. Setiap sudut dalam segitiga siku-siku memiliki sisi-sisi yang berhubungan dengannya, yaitu sisi miring (hypotenuse), sisi depan (opposite), dan sisi samping (adjacent).

Pengertian Sudut dan Sisi dalam Segitiga Siku-Siku

Dalam segitiga siku-siku, sudut siku-siku adalah sudut yang berukuran 90 derajat. Sisi miring adalah sisi yang berhadapan dengan sudut siku-siku. Sisi depan adalah sisi yang berhadapan dengan sudut yang sedang kita tinjau, dan sisi samping adalah sisi yang berdekatan dengan sudut yang sedang kita tinjau.

Diagram Hubungan Sudut, Sisi, dan Fungsi Trigonometri

Berikut adalah diagram yang menunjukkan hubungan antara sudut, sisi, dan fungsi trigonometri dalam segitiga siku-siku:

 adalah sisi terpanjang dalam segitiga siku-siku. Sisi depan (opposite) adalah sisi yang berhadapan dengan sudut yang sedang kita tinjau. Sisi samping (adjacent) adalah sisi yang berdekatan dengan sudut yang sedang kita tinjau. Sinus (sin) adalah rasio antara sisi depan dan sisi miring. Cosinus (cos) adalah rasio antara sisi samping dan sisi miring. Tangent (tan) adalah rasio antara sisi depan dan sisi samping.)

Contoh Soal

Misalnya, kita memiliki segitiga siku-siku dengan sudut A = 30 derajat, sisi depan = 5 cm, dan sisi miring = 10 cm. Kita ingin menentukan panjang sisi samping (adjacent).

Kita dapat menggunakan fungsi trigonometri cosinus (cos) untuk menyelesaikan masalah ini. Cosinus sudut A adalah rasio antara sisi samping dan sisi miring.

cos A = sisi samping / sisi miring

Kita tahu bahwa cos 30 derajat = √3 / 2, sisi miring = 10 cm, dan kita ingin mencari sisi samping.

√3 / 2 = sisi samping / 10 cm

Untuk mencari sisi samping, kita dapat mengalikan kedua sisi persamaan dengan 10 cm:

sisi samping = (√3 / 2) * 10 cm = 5√3 cm

Jadi, panjang sisi samping adalah 5√3 cm.

Grafik Fungsi Trigonometri

Grafik fungsi trigonometri merupakan representasi visual dari nilai fungsi sinus, cosinus, dan tangen untuk setiap sudut. Grafik ini membantu kita memahami sifat-sifat dan pola yang terjadi dalam fungsi trigonometri. Grafik fungsi trigonometri memiliki karakteristik yang unik dan penting untuk dipahami dalam berbagai aplikasi matematika dan fisika.

Grafik Fungsi Sinus

Grafik fungsi sinus (y = sin x) berbentuk gelombang yang berulang secara periodik. Gelombang ini memiliki puncak dan lembah yang menunjukkan nilai maksimum dan minimum fungsi. Karakteristik utama grafik fungsi sinus meliputi:

• Periode: Jarak horizontal yang dibutuhkan fungsi untuk menyelesaikan satu siklus penuh. Periode fungsi sinus adalah 2π.
• Amplitudo: Jarak vertikal antara garis tengah dan titik puncak atau lembah. Amplitudo fungsi sinus adalah 1.
• Garis Tengah: Garis horizontal yang membagi grafik menjadi dua bagian yang sama. Garis tengah fungsi sinus adalah sumbu x.

Grafik Fungsi Cosinus

Grafik fungsi cosinus (y = cos x) juga berbentuk gelombang yang berulang secara periodik. Mirip dengan fungsi sinus, grafik fungsi cosinus memiliki puncak dan lembah yang menunjukkan nilai maksimum dan minimum fungsi. Karakteristik utama grafik fungsi cosinus meliputi:

• Periode: Jarak horizontal yang dibutuhkan fungsi untuk menyelesaikan satu siklus penuh. Periode fungsi cosinus adalah 2π.
• Amplitudo: Jarak vertikal antara garis tengah dan titik puncak atau lembah. Amplitudo fungsi cosinus adalah 1.
• Garis Tengah: Garis horizontal yang membagi grafik menjadi dua bagian yang sama. Garis tengah fungsi cosinus adalah sumbu x.

Grafik Fungsi Tangen

Grafik fungsi tangen (y = tan x) memiliki bentuk yang berbeda dari fungsi sinus dan cosinus. Grafik fungsi tangen memiliki asimptot vertikal yang terjadi pada setiap nilai x yang membuat cos x = 0. Karakteristik utama grafik fungsi tangen meliputi:

• Periode: Jarak horizontal yang dibutuhkan fungsi untuk menyelesaikan satu siklus penuh. Periode fungsi tangen adalah π.
• Asimptot Vertikal: Garis vertikal yang tidak pernah dipotong oleh grafik fungsi. Asimptot vertikal fungsi tangen terjadi pada x = (π/2) + kπ, dengan k adalah bilangan bulat.
• Garis Tengah: Tidak ada garis tengah pada grafik fungsi tangen.

Contoh Soal Analisis Grafik Fungsi Trigonometri

Sebuah roda Ferris memiliki diameter 50 meter dan berputar dengan kecepatan konstan. Seorang anak menaiki roda Ferris dan posisinya terhadap tanah dapat dimodelkan dengan fungsi sinus. Jika tinggi anak dari tanah dapat dinyatakan sebagai h(t) = 25 + 25 sin (πt/10), dengan t adalah waktu dalam detik, tentukan:

1. Amplitudo fungsi h(t) dan apa artinya dalam konteks soal?
2. Periode fungsi h(t) dan apa artinya dalam konteks soal?
3. Tinggi maksimum dan minimum anak dari tanah?

Persamaan Trigonometri

Persamaan trigonometri adalah persamaan yang melibatkan fungsi trigonometri, seperti sinus (sin), cosinus (cos), dan tangen (tan). Persamaan ini dapat digunakan untuk menyelesaikan berbagai masalah yang melibatkan sudut, panjang sisi, dan hubungan antar keduanya.

Jenis-jenis Persamaan Trigonometri

Persamaan trigonometri dapat dibedakan berdasarkan bentuk dan kompleksitasnya. Berikut adalah beberapa jenis persamaan trigonometri yang umum ditemui:

• Persamaan trigonometri sederhana: Persamaan ini hanya melibatkan satu fungsi trigonometri dan satu variabel. Contohnya: sin x = 1/2.
• Persamaan trigonometri kompleks: Persamaan ini melibatkan lebih dari satu fungsi trigonometri, lebih dari satu variabel, atau kombinasi keduanya. Contohnya: sin x + cos x = 1.
• Persamaan trigonometri identik: Persamaan ini berlaku untuk semua nilai variabel. Contohnya: sin^2 x + cos^2 x = 1.

Aplikasi Trigonometri

Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut dalam segitiga. Aplikasi trigonometri sangat luas, dan ilmu ini memainkan peran penting dalam berbagai bidang, termasuk navigasi, astronomi, arsitektur, dan banyak lagi.

Navigasi

Trigonometri digunakan dalam navigasi untuk menentukan posisi dan arah. Misalnya, pelaut menggunakan trigonometri untuk menentukan lokasi mereka di laut dengan menggunakan sudut antara bintang-bintang dan cakrawala.

• Sistem navigasi GPS juga menggunakan trigonometri untuk menentukan lokasi perangkat dengan menghitung jarak dari beberapa satelit.

Astronomi

Trigonometri digunakan dalam astronomi untuk menentukan jarak dan ukuran benda langit. Misalnya, astronom menggunakan trigonometri untuk menentukan jarak ke bintang-bintang dengan menggunakan paralaks, yaitu perubahan posisi bintang yang terlihat dari dua titik yang berbeda di orbit Bumi.

• Trigonometri juga digunakan untuk menentukan ukuran planet dan bintang, serta untuk mempelajari gerakan benda-benda langit.

Arsitektur

Trigonometri digunakan dalam arsitektur untuk merancang struktur yang kuat dan stabil. Misalnya, arsitek menggunakan trigonometri untuk menghitung sudut atap, kekuatan balok, dan stabilitas struktur.

• Trigonometri juga digunakan untuk merancang bangunan yang indah dan estetis, dengan mempertimbangkan sudut pandang dan proporsi.

Contoh Soal Penerapan Trigonometri dalam Kehidupan Nyata

Seorang tukang kayu ingin membangun atap rumah dengan kemiringan 30 derajat. Jika lebar rumah 10 meter, berapa panjang atap yang dibutuhkan?

Kita dapat menggunakan trigonometri untuk menyelesaikan masalah ini. Sudut kemiringan atap adalah 30 derajat, dan lebar rumah adalah 10 meter. Panjang atap adalah sisi miring segitiga siku-siku, dan lebar rumah adalah sisi alas.

Kita dapat menggunakan fungsi trigonometri sinus untuk menghitung panjang atap:

“`
sin(30 derajat) = sisi alas / sisi miring
“`

“`
sin(30 derajat) = 10 meter / sisi miring
“`

“`
sisi miring = 10 meter / sin(30 derajat)
“`

“`
sisi miring = 20 meter
“`

Jadi, panjang atap yang dibutuhkan adalah 20 meter.

Contoh Kasus Penggunaan Trigonometri dalam Memecahkan Masalah

Seorang surveyor ingin menentukan tinggi sebuah pohon. Dia berdiri 10 meter dari pohon dan mengukur sudut elevasi puncak pohon dari posisinya adalah 30 derajat. Berapakah tinggi pohon tersebut?

Kita dapat menggunakan trigonometri untuk menyelesaikan masalah ini. Sudut elevasi adalah 30 derajat, dan jarak surveyor ke pohon adalah 10 meter. Tinggi pohon adalah sisi tegak segitiga siku-siku, dan jarak surveyor ke pohon adalah sisi alas.

Kita dapat menggunakan fungsi trigonometri tangen untuk menghitung tinggi pohon:

“`
tan(30 derajat) = sisi tegak / sisi alas
“`

“`
tan(30 derajat) = tinggi pohon / 10 meter
“`

“`
tinggi pohon = 10 meter * tan(30 derajat)
“`

“`
tinggi pohon = 5.77 meter
“`

Jadi, tinggi pohon tersebut adalah 5.77 meter.

Soal HOTS Trigonometri

Soal HOTS (Higher Order Thinking Skills) dalam trigonometri bertujuan untuk menguji kemampuan berpikir tingkat tinggi siswa, seperti menganalisis, mensintesis, dan mengevaluasi. Soal-soal ini tidak hanya menuntut pemahaman konsep, tetapi juga kemampuan untuk menerapkannya dalam situasi yang kompleks dan tidak familiar.

Strategi Penyelesaian Soal HOTS Trigonometri

Strategi penyelesaian soal HOTS trigonometri meliputi:

• Memahami Konsep Dasar: Pastikan Anda menguasai konsep dasar trigonometri, seperti rumus-rumus identitas, fungsi trigonometri, dan hubungan antar sudut.
• Menganalisis Soal: Bacalah soal dengan cermat dan identifikasi informasi yang diberikan dan yang ingin dicari. Tuliskan informasi penting dan gambarlah sketsa jika diperlukan.
• Menentukan Strategi: Pilih strategi penyelesaian yang tepat berdasarkan jenis soal dan informasi yang diberikan. Terkadang, Anda perlu menggabungkan beberapa konsep trigonometri untuk menemukan solusi.
• Melakukan Perhitungan: Gunakan rumus-rumus trigonometri yang tepat dan selesaikan perhitungan dengan teliti.
• Memeriksa Jawaban: Pastikan jawaban Anda masuk akal dan sesuai dengan konteks soal. Periksa kembali langkah-langkah penyelesaian Anda.

Contoh Soal HOTS Trigonometri

Berikut adalah contoh soal HOTS trigonometri yang melibatkan analisis, sintesis, dan evaluasi:

Analisis

Sebuah pesawat terbang lepas landas dengan sudut elevasi 30°. Setelah terbang sejauh 500 meter, pesawat tersebut mengubah arah terbang dengan sudut elevasi 45°. Berapa ketinggian pesawat setelah terbang sejauh 1000 meter?

Sintesis

Tentukan nilai dari tan(x) + tan(y) jika diketahui bahwa sin(x + y) = 1/2 dan cos(x – y) = √3/2, dengan 0° ≤ x, y ≤ 90°.

Evaluasi

Perhatikan pernyataan berikut: “Jika sin(x) = cos(y), maka x + y = 90°”. Apakah pernyataan tersebut benar? Jelaskan alasan Anda.

Tips dan Trik Menyelesaikan Soal Trigonometri

Trigonometri merupakan salah satu cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga. Materi ini seringkali dianggap sulit oleh banyak siswa, terutama dalam menyelesaikan soal-soal yang rumit. Namun, dengan strategi yang tepat dan pemahaman yang kuat tentang konsep dasar trigonometri, kamu bisa menaklukkan soal-soal trigonometri dengan mudah dan cepat.

Memahami Konsep Dasar

Langkah pertama untuk menaklukkan soal trigonometri adalah dengan memahami konsep dasar trigonometri. Pastikan kamu memahami definisi dari sinus, cosinus, tangen, dan kebalikannya (cosecan, secan, cotangen). Pelajari dengan baik rumus-rumus dasar trigonometri, seperti rumus sudut istimewa, rumus penjumlahan dan pengurangan sudut, rumus sudut ganda, dan rumus perkalian sudut. Kemampuan untuk memahami dan menerapkan rumus-rumus ini akan menjadi kunci untuk menyelesaikan soal-soal trigonometri dengan cepat dan tepat.

Mengenali Pola dan Hubungan

Soal trigonometri seringkali mengandung pola dan hubungan tertentu yang dapat membantu kamu dalam menyelesaikannya. Misalnya, jika kamu menemukan soal yang melibatkan sudut-sudut istimewa, kamu bisa langsung menggunakan nilai trigonometri sudut istimewa yang sudah kamu hafal. Selain itu, perhatikan hubungan antara fungsi trigonometri, seperti hubungan antara sinus dan cosinus, tangen dan cotangen, serta hubungan antara fungsi trigonometri dengan identitas trigonometri. Dengan memahami pola dan hubungan ini, kamu bisa menemukan solusi yang lebih cepat dan efisien.

Memanfaatkan Identitas Trigonometri

Identitas trigonometri merupakan persamaan yang selalu benar untuk semua nilai sudut. Identitas trigonometri sangat berguna untuk menyederhanakan persamaan trigonometri, mengubah bentuk persamaan, atau mencari nilai fungsi trigonometri yang tidak diketahui. Ada banyak identitas trigonometri yang bisa kamu pelajari, seperti identitas Pythagoras, identitas sudut ganda, identitas sudut rangkap, dan identitas perkalian sudut. Semakin banyak identitas trigonometri yang kamu kuasai, semakin mudah kamu menyelesaikan soal-soal trigonometri yang rumit.

Menggunakan Grafik dan Diagram

Grafik dan diagram dapat menjadi alat bantu yang efektif untuk memahami dan menyelesaikan soal trigonometri. Misalnya, dengan menggunakan grafik fungsi trigonometri, kamu bisa melihat pola dan hubungan antara sudut dan nilai fungsi trigonometri. Diagram juga bisa membantu kamu dalam memvisualisasikan masalah dan menemukan solusi yang tepat. Gunakan grafik dan diagram untuk membantu kamu memahami konsep dan menyelesaikan soal-soal trigonometri dengan lebih mudah.

Berlatih dengan Soal-Soal

Seperti halnya mata pelajaran lain, latihan yang konsisten adalah kunci untuk menguasai trigonometri. Semakin banyak soal yang kamu kerjakan, semakin terbiasa kamu dengan berbagai jenis soal dan strategi penyelesaiannya. Carilah soal-soal latihan dari buku teks, internet, atau dari guru kamu. Jangan ragu untuk bertanya jika kamu menemukan kesulitan dalam menyelesaikan soal tertentu. Melalui latihan yang konsisten, kamu akan meningkatkan kemampuan dan kepercayaan diri kamu dalam menghadapi soal-soal trigonometri.

Tabel Rumus dan Identitas Trigonometri

Rumus	Keterangan
sin2 θ + cos2 θ = 1	Identitas Pythagoras
tan θ = sin θ / cos θ	Definisi tangen
cot θ = cos θ / sin θ	Definisi cotangen
sin (α + β) = sin α cos β + cos α sin β	Rumus penjumlahan sudut
cos (α + β) = cos α cos β – sin α sin β	Rumus penjumlahan sudut
tan (α + β) = (tan α + tan β) / (1 – tan α tan β)	Rumus penjumlahan sudut
sin 2θ = 2 sin θ cos θ	Rumus sudut ganda
cos 2θ = cos2 θ – sin2 θ = 1 – 2 sin2 θ = 2 cos2 θ – 1	Rumus sudut ganda
tan 2θ = 2 tan θ / (1 – tan2 θ)	Rumus sudut ganda

Contoh Soal dan Jawaban Trigonometri

Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi dalam segitiga. Konsep trigonometri diaplikasikan dalam berbagai bidang, seperti arsitektur, navigasi, dan fisika. Berikut ini adalah contoh soal trigonometri beserta langkah-langkah penyelesaian dan jawabannya, yang disusun berdasarkan tingkat kesulitan.

Soal Trigonometri Dasar

Berikut adalah beberapa contoh soal trigonometri dasar beserta jawabannya:

• Soal 1: Diketahui segitiga siku-siku ABC dengan sudut siku-siku di C. Jika panjang sisi AB = 5 cm dan BC = 4 cm, tentukan nilai sin A.
  Penyelesaian:
  – Gunakan rumus sinus: sin A = sisi depan / sisi miring.
  – Sisi depan sudut A adalah BC = 4 cm.
  – Sisi miring adalah AB = 5 cm.
  – Jadi, sin A = 4/5.
  Jawaban: sin A = 4/5.
• Soal 2: Tentukan nilai cos 60°.
  Penyelesaian:
  – Gunakan tabel trigonometri atau kalkulator.
  – Nilai cos 60° adalah 1/2.
  Jawaban: cos 60° = 1/2.

Soal Trigonometri Menengah

Berikut adalah contoh soal trigonometri tingkat menengah beserta jawabannya:

• Soal 3: Diketahui segitiga ABC dengan sudut A = 30°, sudut B = 60°, dan panjang sisi AC = 10 cm. Tentukan panjang sisi AB.
  Penyelesaian:
  – Gunakan aturan sinus: a/sin A = b/sin B = c/sin C.
  – Diketahui a = AC = 10 cm, A = 30°, dan B = 60°.
  – Cari nilai sin C: C = 180° – A – B = 180° – 30° – 60° = 90°.
  – Jadi, sin C = sin 90° = 1.
  – Gunakan aturan sinus untuk mencari b = AB:
  b/sin B = a/sin A
  b/sin 60° = 10/sin 30°
  b = (10 * sin 60°) / sin 30°
  b = (10 * √3/2) / (1/2)
  b = 10√3 cm.
  Jawaban: Panjang sisi AB = 10√3 cm.
• Soal 4: Tentukan nilai tan 45°.
  Penyelesaian:
  – Gunakan tabel trigonometri atau kalkulator.
  – Nilai tan 45° adalah 1.
  Jawaban: tan 45° = 1.

Soal Trigonometri Sulit

Berikut adalah contoh soal trigonometri tingkat sulit beserta jawabannya:

• Soal 5: Buktikan identitas trigonometri: sin²x + cos²x = 1.
  Penyelesaian:
  – Gunakan rumus Pythagoras: a² + b² = c².
  – Dalam segitiga siku-siku, sisi miring (c) adalah hipotenusa, sisi depan (a) adalah sisi yang berhadapan dengan sudut x, dan sisi samping (b) adalah sisi yang berdekatan dengan sudut x.
  – Jadi, a² + b² = c² dapat ditulis sebagai sin²x + cos²x = 1.
  Jawaban: Identitas trigonometri sin²x + cos²x = 1 terbukti.
• Soal 6: Tentukan nilai x yang memenuhi persamaan trigonometri: sin x = 1/2, 0° ≤ x ≤ 360°.
  Penyelesaian:
  – Gunakan tabel trigonometri atau kalkulator.
  – Nilai sin x = 1/2 terjadi pada x = 30° dan x = 150°.
  Jawaban: x = 30° dan x = 150°.

Aplikasi Trigonometri dalam Kehidupan Sehari-hari

Trigonometri memiliki aplikasi yang luas dalam kehidupan sehari-hari, seperti:

• Arsitektur: Trigonometri digunakan untuk menghitung sudut dan panjang sisi dalam desain bangunan, seperti atap, tangga, dan jembatan.
• Navigasi: Trigonometri digunakan untuk menentukan posisi dan arah kapal laut dan pesawat terbang.
• Fisika: Trigonometri digunakan untuk menganalisis gerakan benda, seperti proyektil dan gelombang.

Pemungkas

Melalui contoh soal dan jawaban trigonometri yang telah dibahas, diharapkan Anda dapat memahami konsep trigonometri dengan lebih baik dan mampu menerapkannya dalam berbagai situasi. Ingat, kunci keberhasilan dalam mempelajari trigonometri adalah latihan dan pemahaman konsep yang mendalam. Dengan tekun berlatih dan memahami konsep, Anda akan mampu menaklukkan tantangan trigonometri dengan percaya diri.