Contoh Soal Kesebangunan: Menguak Rahasia Bangun Datar yang Serupa

Pernahkah Anda memperhatikan bagaimana sebuah foto dapat diperbesar atau diperkecil tanpa mengubah bentuknya? Atau bagaimana peta mampu merepresentasikan wilayah yang luas dalam ukuran yang lebih kecil? Di balik keajaiban ini, terdapat konsep matematika yang menarik bernama kesebangunan. Kesebangunan dalam geometri menjelaskan hubungan antara dua bangun datar yang memiliki bentuk sama tetapi ukuran yang berbeda. Dalam artikel ini, kita akan menjelajahi dunia contoh soal kesebangunan, mulai dari pengertian hingga aplikasi dalam kehidupan sehari-hari.

Kesebangunan merupakan konsep fundamental dalam geometri yang memiliki peran penting dalam berbagai bidang, seperti arsitektur, desain, dan bahkan ilmu ukur. Dengan memahami konsep ini, kita dapat menyelesaikan berbagai masalah yang melibatkan perbandingan sisi, sudut, luas, dan volume bangun datar yang sebangun.

Pengertian Kesebangunan

Kesebangunan dalam geometri adalah konsep yang menjelaskan hubungan antara dua bangun geometri yang memiliki bentuk yang sama, tetapi ukurannya berbeda. Dua bangun dikatakan sebangun jika semua sudut yang bersesuaian pada kedua bangun tersebut sama besar, dan sisi-sisi yang bersesuaian memiliki perbandingan yang sama.

Contoh Kesebangunan dalam Kehidupan Sehari-hari

Kesebangunan dapat kita temui di berbagai benda di sekitar kita. Berikut beberapa contohnya:

• Foto dan cetak foto. Foto yang kita ambil dengan kamera memiliki bentuk dan ukuran yang sama dengan cetak fotonya, hanya saja ukuran cetak fotonya lebih besar.
• Model pesawat dan pesawat sebenarnya. Model pesawat mainan biasanya dibuat dengan bentuk yang sama dengan pesawat sebenarnya, hanya saja ukurannya jauh lebih kecil.
• Peta dan wilayah sebenarnya. Peta adalah representasi grafis dari wilayah tertentu, yang dibuat dengan skala tertentu. Peta dan wilayah sebenarnya memiliki bentuk yang sama, tetapi ukurannya berbeda.

Ciri-ciri Dua Bangun Datar yang Sebangun

Dua bangun datar dikatakan sebangun jika memenuhi ciri-ciri berikut:

• Sudut-sudut yang bersesuaian sama besar. Artinya, jika dua sudut pada bangun pertama memiliki besar yang sama dengan dua sudut pada bangun kedua, maka kedua bangun tersebut sebangun.
• Sisi-sisi yang bersesuaian memiliki perbandingan yang sama. Artinya, jika panjang sisi pertama pada bangun pertama sebanding dengan panjang sisi pertama pada bangun kedua, dan panjang sisi kedua pada bangun pertama sebanding dengan panjang sisi kedua pada bangun kedua, dan seterusnya, maka kedua bangun tersebut sebangun.

Jenis-jenis Soal Kesebangunan

Soal kesebangunan dapat dijumpai dalam berbagai bentuk dan jenis, tergantung pada bangun datar yang dilibatkan. Untuk memahami lebih dalam, mari kita bahas jenis-jenis soal kesebangunan berdasarkan bentuk bangun datar yang umum ditemukan.

Soal Kesebangunan Segitiga

Soal kesebangunan segitiga merupakan jenis soal yang paling sering ditemui. Dalam soal ini, Anda diminta untuk menentukan apakah dua segitiga sebangun atau tidak, serta mencari panjang sisi atau sudut yang belum diketahui.

• Contoh Soal: Diketahui segitiga ABC dengan panjang sisi AB = 6 cm, BC = 8 cm, dan AC = 10 cm. Segitiga DEF memiliki panjang sisi DE = 9 cm, EF = 12 cm, dan DF = 15 cm. Apakah kedua segitiga tersebut sebangun?
• Metode Penyelesaian: Untuk menentukan apakah dua segitiga sebangun, kita dapat menggunakan beberapa metode, seperti:
• Perbandingan Sisi: Periksa apakah perbandingan sisi-sisi yang bersesuaian dari kedua segitiga sama. Dalam contoh soal di atas, perbandingan sisi AB/DE = 6/9 = 2/3, BC/EF = 8/12 = 2/3, dan AC/DF = 10/15 = 2/3. Karena perbandingan sisi-sisi yang bersesuaian sama, maka segitiga ABC dan DEF sebangun.
• Perbandingan Sudut: Periksa apakah sudut-sudut yang bersesuaian dari kedua segitiga sama besar. Jika sudut-sudut yang bersesuaian sama besar, maka kedua segitiga tersebut sebangun.
• Sisi-Sudut-Sisi (SAS): Jika dua sisi yang bersesuaian dari dua segitiga sebanding, dan sudut yang diapit oleh sisi-sisi tersebut sama besar, maka kedua segitiga tersebut sebangun.
• Sudut-Sisi-Sudut (ASA): Jika dua sudut yang bersesuaian dari dua segitiga sama besar, dan sisi yang diapit oleh sudut-sudut tersebut sebanding, maka kedua segitiga tersebut sebangun.

Soal Kesebangunan Persegi Panjang

Soal kesebangunan persegi panjang biasanya melibatkan perbandingan sisi-sisi dan diagonal dari dua persegi panjang yang sebangun. Soal ini seringkali berkaitan dengan skala dan pembesaran.

• Contoh Soal: Diketahui persegi panjang ABCD dengan panjang AB = 8 cm dan lebar BC = 6 cm. Persegi panjang EFGH sebangun dengan persegi panjang ABCD dan memiliki panjang EF = 12 cm. Tentukan lebar persegi panjang EFGH.
• Metode Penyelesaian: Karena kedua persegi panjang sebangun, maka perbandingan sisi-sisi yang bersesuaian sama. Perbandingan panjang AB/EF = 8/12 = 2/3. Dengan demikian, perbandingan lebar BC/GH juga sama dengan 2/3. Untuk mencari lebar GH, kita dapat menggunakan persamaan BC/GH = 2/3, sehingga GH = (3/2) * BC = (3/2) * 6 cm = 9 cm.

Soal Kesebangunan Trapesium

Soal kesebangunan trapesium umumnya melibatkan perbandingan sisi-sisi sejajar dan tinggi dari dua trapesium yang sebangun. Soal ini seringkali berkaitan dengan skala dan pembesaran.

• Contoh Soal: Diketahui trapesium ABCD dengan panjang sisi sejajar AB = 10 cm dan CD = 6 cm, serta tinggi trapesium 8 cm. Trapesium EFGH sebangun dengan trapesium ABCD dan memiliki panjang sisi sejajar EF = 15 cm. Tentukan tinggi trapesium EFGH.
• Metode Penyelesaian: Karena kedua trapesium sebangun, maka perbandingan sisi-sisi sejajar dan tinggi sama. Perbandingan sisi sejajar AB/EF = 10/15 = 2/3. Dengan demikian, perbandingan tinggi trapesium ABCD/EFGH juga sama dengan 2/3. Untuk mencari tinggi trapesium EFGH, kita dapat menggunakan persamaan ABCD/EFGH = 2/3, sehingga EFGH = (3/2) * ABCD = (3/2) * 8 cm = 12 cm.

Soal Kesebangunan Lingkaran

Soal kesebangunan lingkaran biasanya melibatkan perbandingan jari-jari dan diameter dari dua lingkaran yang sebangun. Soal ini seringkali berkaitan dengan skala dan pembesaran.

• Contoh Soal: Diketahui lingkaran A dengan jari-jari 5 cm. Lingkaran B sebangun dengan lingkaran A dan memiliki diameter 12 cm. Tentukan jari-jari lingkaran B.
• Metode Penyelesaian: Karena kedua lingkaran sebangun, maka perbandingan jari-jari dan diameter sama. Perbandingan jari-jari lingkaran A/B = 5/(12/2) = 5/6. Dengan demikian, perbandingan diameter lingkaran A/B juga sama dengan 5/6. Untuk mencari jari-jari lingkaran B, kita dapat menggunakan persamaan A/B = 5/6, sehingga B = (6/5) * A = (6/5) * 5 cm = 6 cm. Jari-jari lingkaran B adalah 6 cm / 2 = 3 cm.

Soal Kesebangunan dengan Perbandingan Sisi

Dalam geometri, konsep kesebangunan merupakan salah satu topik penting yang membahas hubungan antara dua bangun yang memiliki bentuk sama tetapi ukuran berbeda. Untuk menentukan kesebangunan, salah satu metode yang umum digunakan adalah dengan membandingkan sisi-sisi yang bersesuaian. Artikel ini akan membahas lebih lanjut mengenai konsep perbandingan sisi dalam soal kesebangunan, disertai dengan contoh soal dan cara menentukan panjang sisi yang belum diketahui.

Konsep Perbandingan Sisi dalam Soal Kesebangunan

Perbandingan sisi dalam soal kesebangunan adalah konsep yang menyatakan bahwa perbandingan panjang sisi-sisi yang bersesuaian pada dua bangun sebangun selalu sama. Dengan kata lain, jika dua bangun sebangun, maka perbandingan panjang sisi-sisi yang bersesuaian akan menghasilkan nilai yang sama. Perbandingan sisi ini merupakan dasar untuk menyelesaikan berbagai soal kesebangunan, khususnya untuk menentukan panjang sisi yang belum diketahui.

Contoh Soal Kesebangunan dengan Perbandingan Sisi

Misalnya, kita memiliki dua segitiga sebangun, yaitu segitiga ABC dan segitiga DEF. Diketahui panjang sisi AB = 6 cm, BC = 8 cm, dan DE = 9 cm. Kita ingin menentukan panjang sisi EF.

Karena segitiga ABC dan DEF sebangun, maka perbandingan sisi-sisi yang bersesuaian sama. Perbandingan sisi AB dan DE adalah 6/9 = 2/3. Dengan demikian, perbandingan sisi BC dan EF juga sama, yaitu 2/3.

Dari perbandingan sisi BC dan EF, kita dapat menentukan panjang sisi EF sebagai berikut:

EF/BC = 2/3
EF/8 = 2/3
EF = (2/3) * 8
EF = 16/3 cm

Jadi, panjang sisi EF adalah 16/3 cm.

Cara Menentukan Panjang Sisi yang Belum Diketahui

Untuk menentukan panjang sisi yang belum diketahui pada soal kesebangunan dengan perbandingan sisi, langkah-langkah yang dapat dilakukan adalah sebagai berikut:

1. Identifikasi sisi-sisi yang bersesuaian pada kedua bangun sebangun.
2. Tentukan perbandingan sisi-sisi yang diketahui.
3. Gunakan perbandingan tersebut untuk menentukan panjang sisi yang belum diketahui.

Dalam menentukan perbandingan sisi, pastikan untuk membandingkan sisi-sisi yang bersesuaian, yaitu sisi yang memiliki posisi yang sama pada kedua bangun sebangun. Selain itu, perhatikan bahwa perbandingan sisi dapat ditulis dalam bentuk pecahan atau desimal.

Soal Kesebangunan dengan Perbandingan Sudut

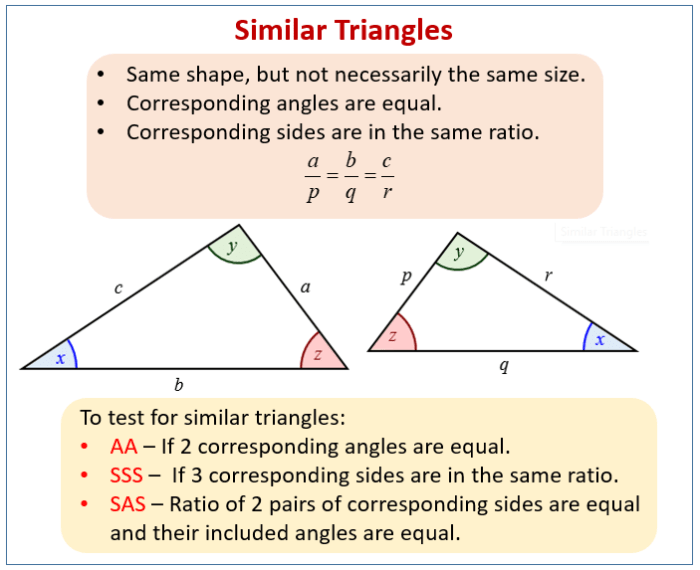
Konsep kesebangunan dalam geometri melibatkan dua bangun datar yang memiliki bentuk sama namun ukuran berbeda. Salah satu syarat utama dua bangun datar sebangun adalah perbandingan sudut-sudut yang bersesuaian sama besar. Dalam artikel ini, kita akan membahas lebih lanjut mengenai konsep perbandingan sudut dalam soal kesebangunan dan bagaimana menerapkannya untuk menentukan besar sudut yang belum diketahui.

Konsep Perbandingan Sudut dalam Kesebangunan

Perbandingan sudut dalam soal kesebangunan merupakan konsep yang menyatakan bahwa sudut-sudut yang bersesuaian pada dua bangun datar sebangun memiliki besar yang sama. Dengan kata lain, jika dua bangun datar sebangun, maka sudut-sudut yang bersesuaian pada kedua bangun tersebut akan memiliki nilai yang sama.

Contoh Soal Kesebangunan dengan Perbandingan Sudut

Perhatikan gambar segitiga ABC dan segitiga DEF di bawah ini.

Segitiga ABC dan segitiga DEF sebangun. Sudut A = 60°, sudut B = 80°, sudut C = 40°, dan sudut D = 60°. Tentukan besar sudut E dan sudut F.

Untuk menentukan besar sudut E dan sudut F, kita dapat memanfaatkan konsep perbandingan sudut pada bangun datar sebangun. Karena segitiga ABC dan segitiga DEF sebangun, maka:

• Sudut A = Sudut D = 60°
• Sudut B = Sudut E = 80°
• Sudut C = Sudut F = 40°

Jadi, besar sudut E adalah 80° dan besar sudut F adalah 40°.

Menentukan Besar Sudut yang Belum Diketahui

Untuk menentukan besar sudut yang belum diketahui pada soal kesebangunan dengan perbandingan sudut, ikuti langkah-langkah berikut:

1. Identifikasi sudut-sudut yang sudah diketahui pada kedua bangun datar.
2. Tentukan sudut-sudut yang bersesuaian pada kedua bangun datar.
3. Manfaatkan konsep perbandingan sudut untuk menentukan besar sudut yang belum diketahui.

Contohnya, jika kita memiliki dua segitiga sebangun dan sudut A pada segitiga pertama adalah 70°, dan sudut D pada segitiga kedua bersesuaian dengan sudut A, maka sudut D juga akan bernilai 70°.

Soal Kesebangunan dengan Perbandingan Luas

Kesebangunan merupakan konsep penting dalam geometri yang membahas hubungan antara dua bangun datar yang memiliki bentuk sama tetapi ukuran yang berbeda. Konsep ini erat kaitannya dengan perbandingan sisi-sisi dan luas bangun datar. Salah satu aspek menarik dalam soal kesebangunan adalah perbandingan luas. Artikel ini akan membahas konsep perbandingan luas dalam soal kesebangunan dan memberikan contoh soal beserta cara menyelesaikannya.

Konsep Perbandingan Luas dalam Kesebangunan

Perbandingan luas pada bangun datar sebangun memiliki hubungan erat dengan perbandingan sisi-sisinya. Secara umum, perbandingan luas dua bangun datar sebangun sama dengan kuadrat dari perbandingan sisi-sisi yang bersesuaian.

Jika dua bangun datar sebangun memiliki perbandingan sisi-sisi k, maka perbandingan luasnya adalah k².

Konsep ini berlaku untuk berbagai macam bangun datar, seperti segitiga, persegi, persegi panjang, dan lingkaran.

Contoh Soal Perbandingan Luas

Misalkan kita memiliki dua buah segitiga sebangun, yaitu segitiga ABC dan segitiga DEF. Diketahui bahwa panjang sisi AB adalah 6 cm, BC adalah 8 cm, dan DE adalah 9 cm. Tentukan luas segitiga DEF jika luas segitiga ABC adalah 24 cm².

• Pertama, kita cari perbandingan sisi-sisi kedua segitiga. Karena segitiga ABC dan DEF sebangun, maka perbandingan sisi-sisi yang bersesuaian adalah sama. Misalnya, perbandingan sisi AB dan DE adalah 6 cm : 9 cm = 2/3.
• Selanjutnya, kita gunakan konsep perbandingan luas. Perbandingan luas segitiga ABC dan DEF sama dengan kuadrat dari perbandingan sisi-sisi yang bersesuaian, yaitu (2/3)² = 4/9.
• Diketahui luas segitiga ABC adalah 24 cm². Kita dapat menentukan luas segitiga DEF dengan menggunakan perbandingan luas:

Luas DEF / Luas ABC = (4/9)

Luas DEF / 24 cm² = (4/9)

Luas DEF = (4/9) * 24 cm² = 10,67 cm²

Jadi, luas segitiga DEF adalah 10,67 cm².

Soal Kesebangunan dengan Perbandingan Volume

Perbandingan volume pada bangun ruang sebangun merupakan salah satu konsep penting dalam geometri. Konsep ini mengacu pada hubungan antara volume dua bangun ruang yang sebangun, yang menyatakan bahwa perbandingan volume kedua bangun tersebut sama dengan pangkat tiga dari perbandingan sisi-sisi yang bersesuaian.

Konsep Perbandingan Volume

Perbandingan volume pada bangun ruang sebangun didasarkan pada prinsip bahwa perbandingan volume kedua bangun tersebut sama dengan pangkat tiga dari perbandingan sisi-sisi yang bersesuaian.

Contoh Soal Perbandingan Volume

Misalkan kita memiliki dua kubus, kubus A dan kubus B, yang sebangun. Sisi kubus A adalah 4 cm, sedangkan sisi kubus B adalah 8 cm.

Menentukan Volume Bangun Ruang yang Belum Diketahui

Untuk menentukan volume bangun ruang yang belum diketahui pada soal kesebangunan dengan perbandingan volume, kita dapat menggunakan rumus berikut:

V₁ / V₂ = (s₁ / s₂)³

Keterangan:

* V₁ = Volume bangun ruang pertama
* V₂ = Volume bangun ruang kedua
* s₁ = Sisi bangun ruang pertama
* s₂ = Sisi bangun ruang kedua

Dengan menggunakan rumus ini, kita dapat menentukan volume bangun ruang yang belum diketahui dengan memasukkan nilai-nilai yang sudah diketahui.

Soal Kesebangunan dengan Penerapan di Kehidupan Sehari-hari

Konsep kesebangunan merupakan salah satu konsep penting dalam geometri yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Kesebangunan menggambarkan dua bangun geometri yang memiliki bentuk sama tetapi ukuran berbeda. Dalam artikel ini, kita akan membahas contoh soal kesebangunan yang berkaitan dengan kehidupan sehari-hari, serta bagaimana konsep ini diterapkan dalam berbagai bidang.

Contoh Soal Kesebangunan dalam Kehidupan Sehari-hari

Misalkan Anda ingin memperbesar foto berukuran 4 cm x 6 cm menjadi poster berukuran 20 cm x 30 cm. Perbandingan panjang dan lebar foto dan poster tersebut sama, yaitu 1:5. Artinya, poster tersebut merupakan pembesaran dari foto dengan faktor skala 5. Konsep kesebangunan memastikan bahwa kedua bangun, yaitu foto dan poster, memiliki bentuk yang sama meskipun ukurannya berbeda.

Penerapan Konsep Kesebangunan

Konsep kesebangunan memiliki banyak aplikasi dalam berbagai bidang, seperti:

Pembuatan Peta

Peta merupakan representasi dua dimensi dari suatu wilayah tiga dimensi. Konsep kesebangunan diterapkan untuk menjaga proporsi dan bentuk wilayah yang sebenarnya dalam peta. Misalnya, jika sebuah sungai memiliki panjang 100 km di dunia nyata, maka pada peta dengan skala 1:1.000.000, sungai tersebut akan digambarkan dengan panjang 10 cm.

Desain Bangunan

Arsitek menggunakan konsep kesebangunan dalam desain bangunan untuk memastikan proporsi dan keselarasan antar bagian bangunan. Misalnya, jika sebuah jendela memiliki lebar 1 meter dan tinggi 2 meter, maka jendela lain di bangunan yang sama harus memiliki perbandingan lebar dan tinggi yang sama, meskipun ukurannya berbeda.

Pembesaran Foto

Seperti contoh sebelumnya, pembesaran foto menggunakan konsep kesebangunan untuk menjaga proporsi dan bentuk asli foto. Perbandingan panjang dan lebar foto asli dan foto hasil pembesaran harus sama, sehingga bentuknya tetap sama meskipun ukurannya berubah.

Seni Lukis

Seniman juga menggunakan konsep kesebangunan dalam lukisan untuk menciptakan perspektif dan ilusi kedalaman. Misalnya, garis-garis sejajar pada objek yang jauh tampak bertemu pada titik lenyap pada lukisan, menciptakan ilusi kedalaman.

Tabel Aplikasi Kesebangunan dalam Berbagai Bidang Kehidupan

Bidang	Contoh Aplikasi
Peta	Menjaga proporsi dan bentuk wilayah yang sebenarnya dalam peta.
Desain Bangunan	Memastikan proporsi dan keselarasan antar bagian bangunan.
Pembesaran Foto	Menjaga proporsi dan bentuk asli foto.
Seni Lukis	Menciptakan perspektif dan ilusi kedalaman.
Teknik Sipil	Membuat model bangunan dan infrastruktur.
Arsitektur Lanskap	Merancang taman dan ruang terbuka hijau.

Soal Kesebangunan dengan Kriteria Kesebangunan

Kesebangunan merupakan konsep penting dalam geometri yang berkaitan dengan bentuk-bentuk yang memiliki bentuk yang sama tetapi ukuran yang berbeda. Dua bangun datar dikatakan sebangun jika sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sebanding. Untuk menentukan kesebangunan dua bangun datar, kita dapat menggunakan beberapa kriteria, yaitu:

Kriteria Kesebangunan

Ada tiga kriteria kesebangunan yang umum digunakan dalam menyelesaikan soal, yaitu:

• Sudut-sudut sebangun: Dua bangun datar dikatakan sebangun jika semua sudut yang bersesuaian sama besar.
• Sisi-sisi sebangun: Dua bangun datar dikatakan sebangun jika semua sisi yang bersesuaian sebanding.
• Sisi-sudut sebangun: Dua bangun datar dikatakan sebangun jika dua sisi yang bersesuaian sebanding dan sudut yang diapit oleh kedua sisi tersebut sama besar.

Contoh Soal Kesebangunan

Berikut ini adalah contoh soal yang menggunakan kriteria kesebangunan:

Contoh Soal 1: Kriteria Sudut-Sudut Sebangun

Perhatikan gambar dua segitiga berikut:

Gambarlah dua segitiga dengan sudut-sudut yang sama besar. Misalnya, segitiga ABC dengan sudut A = 60 derajat, sudut B = 80 derajat, dan sudut C = 40 derajat. Kemudian, gambar segitiga DEF dengan sudut D = 60 derajat, sudut E = 80 derajat, dan sudut F = 40 derajat. Kedua segitiga tersebut memiliki sudut-sudut yang sama besar, sehingga memenuhi kriteria sudut-sudut sebangun.

Apakah segitiga ABC dan DEF sebangun? Jelaskan!

Contoh Soal 2: Kriteria Sisi-Sisi Sebangun

Perhatikan gambar dua persegi panjang berikut:

Gambarlah dua persegi panjang dengan sisi-sisi yang sebanding. Misalnya, persegi panjang ABCD dengan panjang AB = 6 cm dan lebar BC = 4 cm. Kemudian, gambar persegi panjang EFGH dengan panjang EF = 9 cm dan lebar FG = 6 cm. Kedua persegi panjang tersebut memiliki sisi-sisi yang sebanding, sehingga memenuhi kriteria sisi-sisi sebangun.

Apakah persegi panjang ABCD dan EFGH sebangun? Jelaskan!

Contoh soal kesebangunan biasanya melibatkan perbandingan sisi-sisi dan sudut-sudut pada bangun datar atau ruang. Nah, konsep perbandingan ini juga bisa kita temui dalam contoh soal kombinasi dan permutasi, lho! Misalnya, dalam menentukan banyak cara memilih 3 orang dari 5 orang untuk menjadi panitia, kita menggunakan kombinasi.

Untuk memahami lebih lanjut tentang contoh soal kombinasi dan permutasi, kamu bisa cek contoh soal kombinasi dan permutasi yang tersedia di situs tersebut. Setelah memahami kombinasi dan permutasi, kamu akan lebih mudah memahami konsep perbandingan dalam contoh soal kesebangunan.

Contoh Soal 3: Kriteria Sisi-Sudut Sebangun

Perhatikan gambar dua segitiga berikut:

Gambarlah dua segitiga dengan dua sisi yang bersesuaian sebanding dan sudut yang diapit oleh kedua sisi tersebut sama besar. Misalnya, segitiga ABC dengan sisi AB = 4 cm, sisi AC = 6 cm, dan sudut A = 60 derajat. Kemudian, gambar segitiga DEF dengan sisi DE = 6 cm, sisi DF = 9 cm, dan sudut D = 60 derajat. Kedua segitiga tersebut memiliki dua sisi yang bersesuaian sebanding dan sudut yang diapit oleh kedua sisi tersebut sama besar, sehingga memenuhi kriteria sisi-sudut sebangun.

Apakah segitiga ABC dan DEF sebangun? Jelaskan!

Cara Menentukan Kesebangunan Dua Bangun Datar

Untuk menentukan kesebangunan dua bangun datar, kita dapat menggunakan salah satu dari tiga kriteria yang telah disebutkan di atas. Langkah-langkahnya adalah sebagai berikut:

1. Identifikasi sudut-sudut yang bersesuaian atau sisi-sisi yang bersesuaian pada kedua bangun datar.
2. Uji kriteria kesebangunan yang dipilih. Jika kriteria terpenuhi, maka kedua bangun datar tersebut sebangun.

Soal Kesebangunan dengan Teorema Pythagoras: Contoh Soal Kesebangunan

Teorema Pythagoras merupakan konsep penting dalam geometri yang dapat digunakan untuk menyelesaikan berbagai masalah, termasuk soal kesebangunan. Teorema ini menghubungkan panjang sisi-sisi dalam segitiga siku-siku, dan dapat membantu kita menentukan panjang sisi yang belum diketahui.

Teorema Pythagoras dan Kesebangunan, Contoh soal kesebangunan

Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat sisi miring (hipotenusa) sama dengan jumlah kuadrat dari kedua sisi lainnya (sisi tegak). Rumus teorema Pythagoras adalah:

a² + b² = c²

Dimana:
– a dan b adalah panjang sisi tegak
– c adalah panjang sisi miring (hipotenusa)

Konsep kesebangunan menyatakan bahwa dua bangun datar dikatakan sebangun jika bentuknya sama tetapi ukurannya berbeda. Dalam bangun datar yang sebangun, perbandingan panjang sisi-sisi yang bersesuaian adalah sama.

Teorema Pythagoras dapat digunakan untuk menyelesaikan soal kesebangunan dengan menentukan panjang sisi yang belum diketahui pada bangun datar sebangun. Jika kita mengetahui panjang sisi-sisi pada satu bangun datar dan perbandingan panjang sisi-sisi yang bersesuaian, kita dapat menggunakan teorema Pythagoras untuk menentukan panjang sisi-sisi pada bangun datar sebangun lainnya.

Kesimpulan

Dengan memahami konsep kesebangunan, kita dapat mengaplikasikannya dalam berbagai situasi kehidupan sehari-hari. Dari desain bangunan hingga pembuatan peta, konsep ini membantu kita menyelesaikan masalah yang melibatkan bentuk dan ukuran. Melalui contoh-contoh soal yang telah dibahas, kita dapat melihat bagaimana kesebangunan menjadi alat yang ampuh untuk memecahkan masalah geometri yang kompleks.